數列應用問題解法拾零
◇ 北京 丁益祥(特級教師)
?
數列應用問題解法拾零
◇北京丁益祥(特級教師)
在日常生活中,人們經常遇到諸如存款付息、堆垛計數、遞推求值、混合濃度等問題,這些問題常常通過建立數列模型來解決.認真分析題意,建立恰當的數列模型,是解決問題的關鍵.
1 存款付息問題


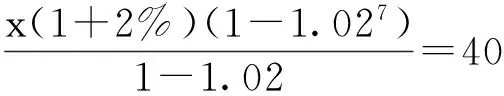

本利和=本金×(1+利率)存期.
2 堆垛計數問題


圖1

由題意知,f(2)比f(1)多最底層:1+2個,即

f(3)比f(2)多最底層:1+2+3個,即
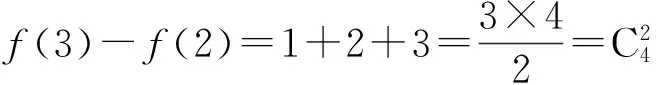
f(4)比f(3)多最底層:1+2+3+4個,即

……
f(n)比f(n-1)多最底層:1+2+…+n個,即

把這n個式子迭加得


3 遞推求值問題

T(a)表示非負實數a的整數部分,例如T(2.6)=2,T(0.2)=0.按此方案, 第6棵樹種植點的坐標應為________;第2 008棵樹種植點的坐標應為________.

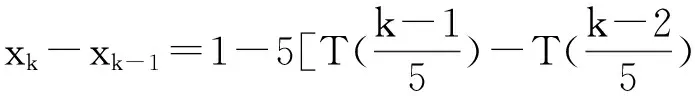
x1=1,
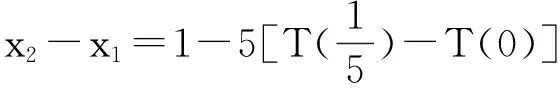
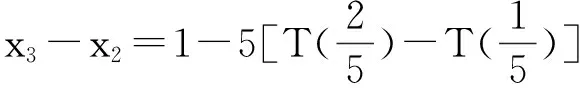
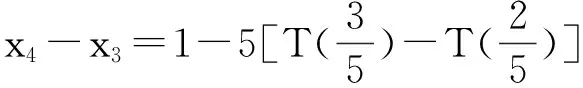
……

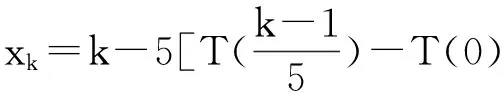
同理, y1=1,
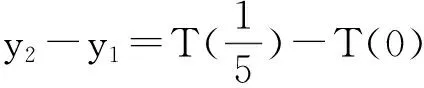

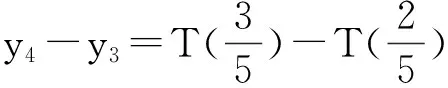
……
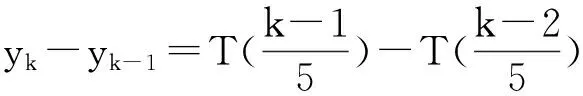


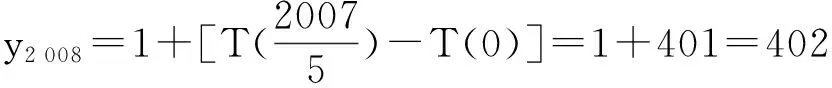
故第6棵樹種植點的坐標應為(1,2),第2 008棵樹種植點的坐標應為(3,402).


注意到x1=1,y1=1,把它們代入遞推關系式,計算得:
數列xn:1,2,3,4,5, 1,2,3,4,5, 1,2,3,4,5,…;
數列yn:1,1,1,1,1, 2,2,2,2,2, 3,3,3,3,3, 4,4,4,4,4,…
因此,第6棵樹種植點的坐標應為(1,2).
又2 008=5×401+3,所以第2 008棵樹種植點的坐標應為(3,402).
4 混合濃度問題


設第n個觀測點處A股河水含沙量為ankg·m-3, B股河水含沙量為bnkg·m-3,n=1,2,3,…,則
a1=2, b1=0.2, a1-b1=1.8.
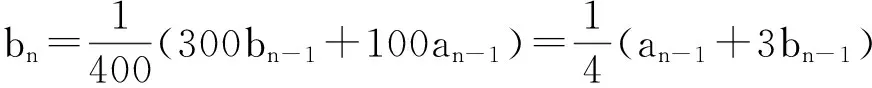

故數列{an-bn}是首項為a1-b1=1.8, 公比為1/2的等比數列,于是an-bn=1.8(1/2)n-1.
令1.8(1/2)n-1<0.01,即2n-1>180.
由于27<180, 28>180,結合指數函數的單調性,得n-1≥8,故n≥9.
因此,從第9個觀測點開始,A股河水的含沙量與B股河水的含沙量之差小于0.01kg·m-3.

北京陳經綸中學)

