精確延時爆破振動速度峰值預測模型

李順波， 楊仁樹， 楊 軍

(1. 中國礦業大學(北京) 力學與建筑工程學院， 北京 100083；2. 北京理工大學 爆炸科學與技術國家重點實驗室， 北京 100081)

?

精確延時爆破振動速度峰值預測模型

李順波1， 楊仁樹1， 楊 軍2

(1. 中國礦業大學(北京) 力學與建筑工程學院， 北京 100083；2. 北京理工大學 爆炸科學與技術國家重點實驗室， 北京 100081)

摘要：根據幾何地震學的基本原理，以單孔爆破振動速度峰值為基礎，按照毫秒延時時間間隔建立精確延時逐孔起爆振動峰值預測模型。不僅可以預測爆破振動速度峰值，而且能夠直觀地展現爆破區域范圍內振動峰值的變化情況，并能從保護區域內振動峰值出發，設定合理的毫秒延時間隔時間。根據現場應用數碼電子雷管的深孔爆破實驗，該方法計算的預測振動峰值與實測振動峰值吻合良好，計算結果可靠性較好，可以在實際工程中推廣使用。

關鍵詞：精確延時； 爆破振動； 預測模型； 振動速度峰值

1引言

爆破技術廣泛應用于堅硬巖體開挖工程中，其中爆破振動被認為是爆破施工中最嚴重的危害之一，如因爆破振動過大引起的滑坡、洞室坍塌、建筑物開裂等災害事故。對爆破振動進行預測是采取有效爆破方案和防護措施的前提，爆破振動強度可以用爆破振動的加速度、速度、位移等來描述，通常以爆破振動峰值振速來描述爆破振動的強度，由于爆破過程及其振動傳播過程的復雜性，實際工程中對于爆破振動峰值預測及衰減規律的研究主要以經驗公式為主，也有一些理論研究，或者采用數值模擬及其他方法的研究〔1〕。

目前采用經驗公式方法( 薩道夫斯基經驗公式等) 的振動預測結果并不理想〔2-3〕，新的爆破振動峰值預測方法勢在必行〔4〕。人們開始探索基于神經網絡、遺傳算法、支持向量機等非線性智能工具進行爆破振動預測的新方法〔5-8〕，并取得一定成果。隨著數碼電子雷管的使用，逐孔起爆成為可能，楊年華等〔9〕給出了一種爆破振動波疊加數值預測方法。本文基于幾何地震學理論，給出了一種爆破振動速度峰值預測方法。

2振動速度峰值預測模型

2.1幾何地震學理論

當地震波在介質中傳播時，在地震波傳播范圍之內的任意一點，都可以記錄波前鋒面到這點的時間，可以將波前鋒面傳播時間記作空間坐標(x,y,z)的函數，即：

t=g(x,y,z)

(1)

由上式就可以確定波前鋒面到達任一點的時間，因此可以確定時間的標量場t(x,y,z)，可以將其定義為時間函數。反之，若在給定一定的時間值ti，則可以由時間函數來確定某一個時刻波前面的位置，從而波前鋒面方程可以表述為：

g(x,y,z)=ti

(2)

若知道了一系列的時間，就可以確定出各自相應的波前面位置。如果將地震波傳播范圍簡化為一個平面或者一條直線，則其時間場函數將分別變為二元和一元函數，即：

t=g(x,y)

(3)

t=g(x)

(4)

假設在某一時刻t1，地震波波陣面位于S1位置。根據惠更斯原理，S1上各點都可以看作是子波源從t1時刻向外發射的球面子波。經過了時間Δt之后，這些子波的“子波前鋒”為半徑等于v(x,y,z)Δt的球面，v(x,y,z)為S1上的波速，這些球面的包絡面S2即是時間t2的波前鋒面，從而可以得知S1和S2之間的法線距離為：

Δn=v(x,y,z)Δt

(5)

時間場波前鋒面如圖1所示。

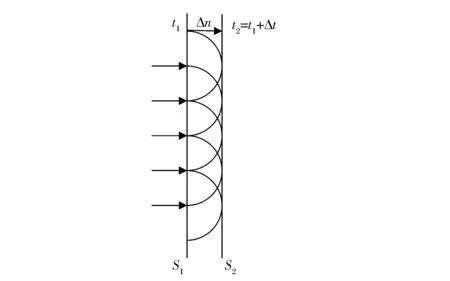
圖1　時間場波前鋒面示意圖Fig.1　Schematic diagram of time field wave front

在爆破工程中，高精度數碼電子雷管由于延時誤差很小，使得其產生的爆破地震波之間的干擾模式可以預測和重復。在單個炮孔起爆的情況下，炸藥爆炸產生的沖擊波經過衰減成為彈性波向外傳播，彈性波傳播速度和巖石介質的性質有一定的關系，同時其向外傳播的過程可以看作一個球形波前鋒面的產生過程。圖2給出了單排炮孔。在孔間毫秒延時間隔為1ms時，其從右到左起爆產生的前鋒面示意圖。

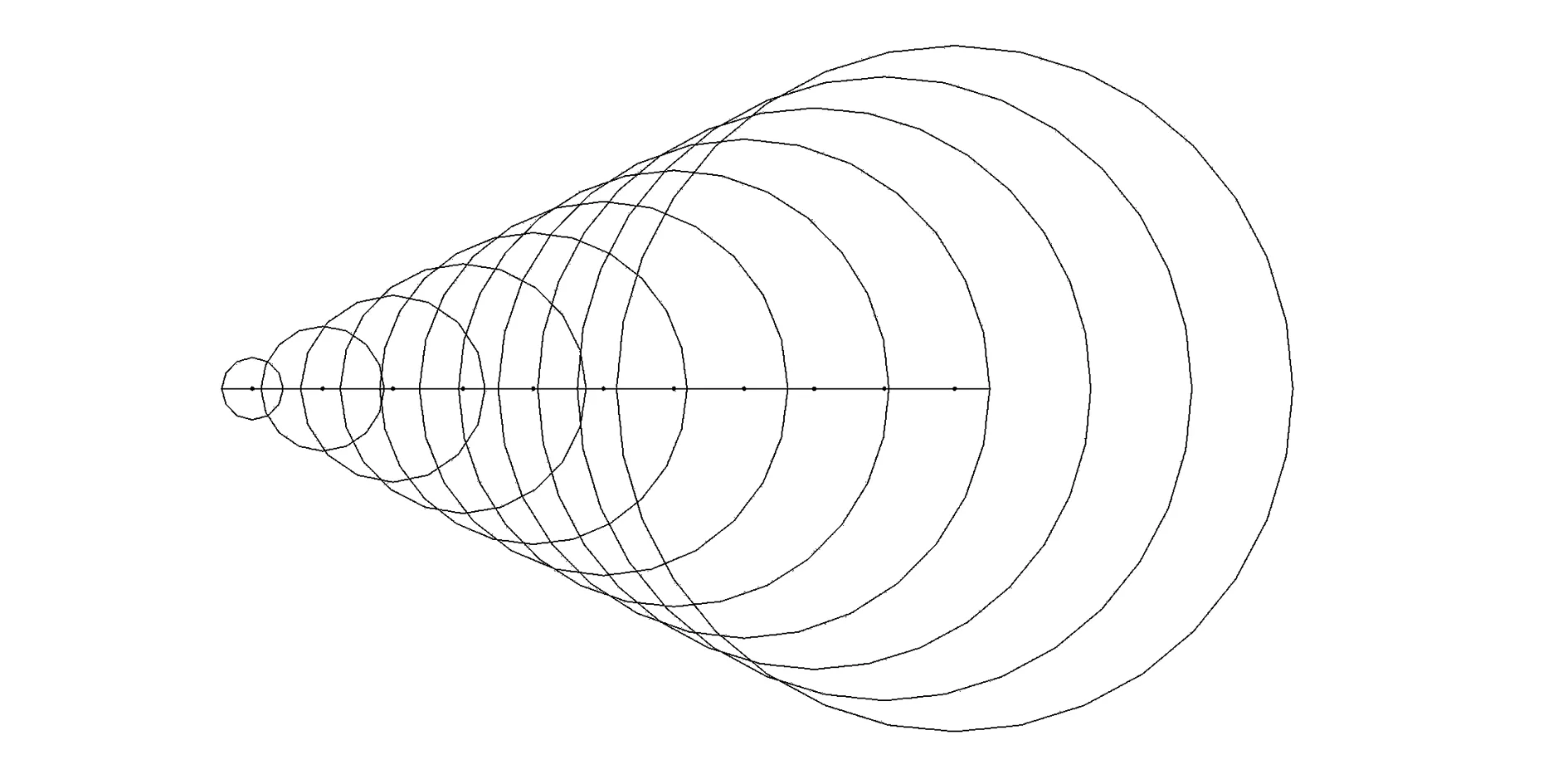
圖2　波前鋒面產生示意圖Fig.2　Schematic diagram of wave front

2.2預測模型的建立和驗證

通過前面的分析看出，可以利用巖石介質的縱波波速確定每個炮孔產生的地震波前鋒面的位置，若知道單個炮孔裝藥情況下爆炸產生的地震波速度峰值大小，即可確定波陣面上速度峰值大小。高精度電子雷管的自身誤差精度在±1ms，可以實現逐孔起爆，因此最終的波形可以考慮三個炮孔產生的地震波影響。由于縱波波速較快，在第一個炮孔起爆之后，到第三個炮孔起爆這段時間內，地震波傳播到較遠距離處，后者很難再對前者產生干擾作用。利用圖2中的爆破區域，建立精確延時條件下爆破振動速度峰值預測模型。炮孔和測點的相對位置如圖3所示，圖中爆破區域的炮孔直徑為140mm，孔深7 ～9m，單孔藥量40 ～90kg，孔間延時18ms。測點M1和M2距爆區142.5m和172.2m。

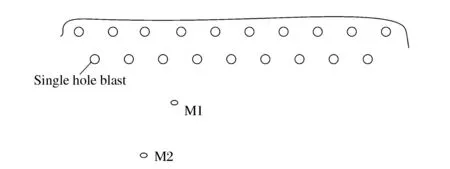
圖3　炮孔和測點位置Fig.3　Position of holes and the measurement points

單孔爆破時兩測點波形如圖4所示，實測波形如圖5所示。從圖4和圖5中可以讀出單個炮孔產生的速度峰值和在兩個測點的速度峰值；建立圖6的速度峰值預測模型(巖石縱波波速3.6km/s)。從圖6中可以看出，在M1和M2點時的波陣面情況，兩個測點到其前面的波前鋒面法向距離都不相等，在其后的時間內兩個測點會受到三個波源的共同影響。因此將在測點之前，由三個波源產生的波前鋒面個數定義為其累積效用，由兩個測點在單孔波形中的爆破振動速度峰值可以確定其具體強度，從而得到測點在所有炮孔起爆后的爆破振動速度峰值。

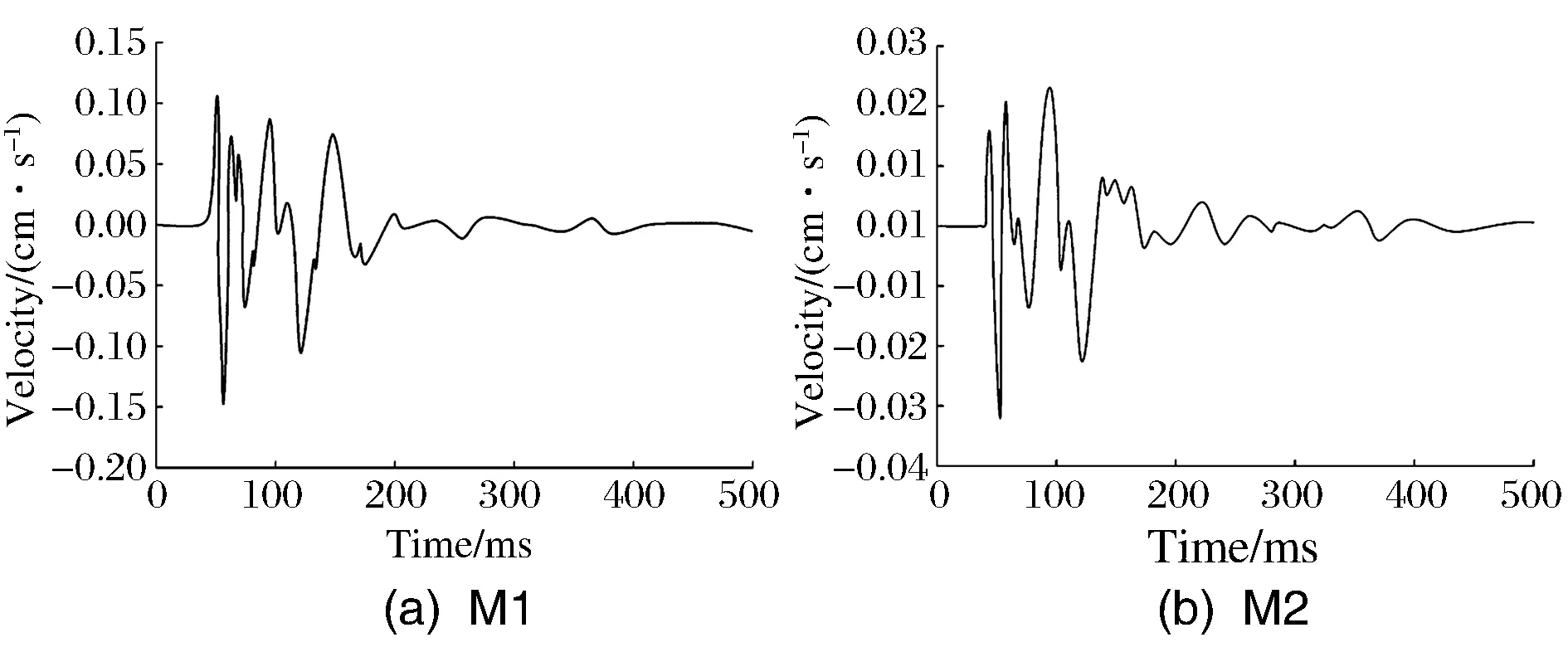
圖4　單孔爆破時兩測點波形Fig.4　Two measurement points waveform in single hole blasting

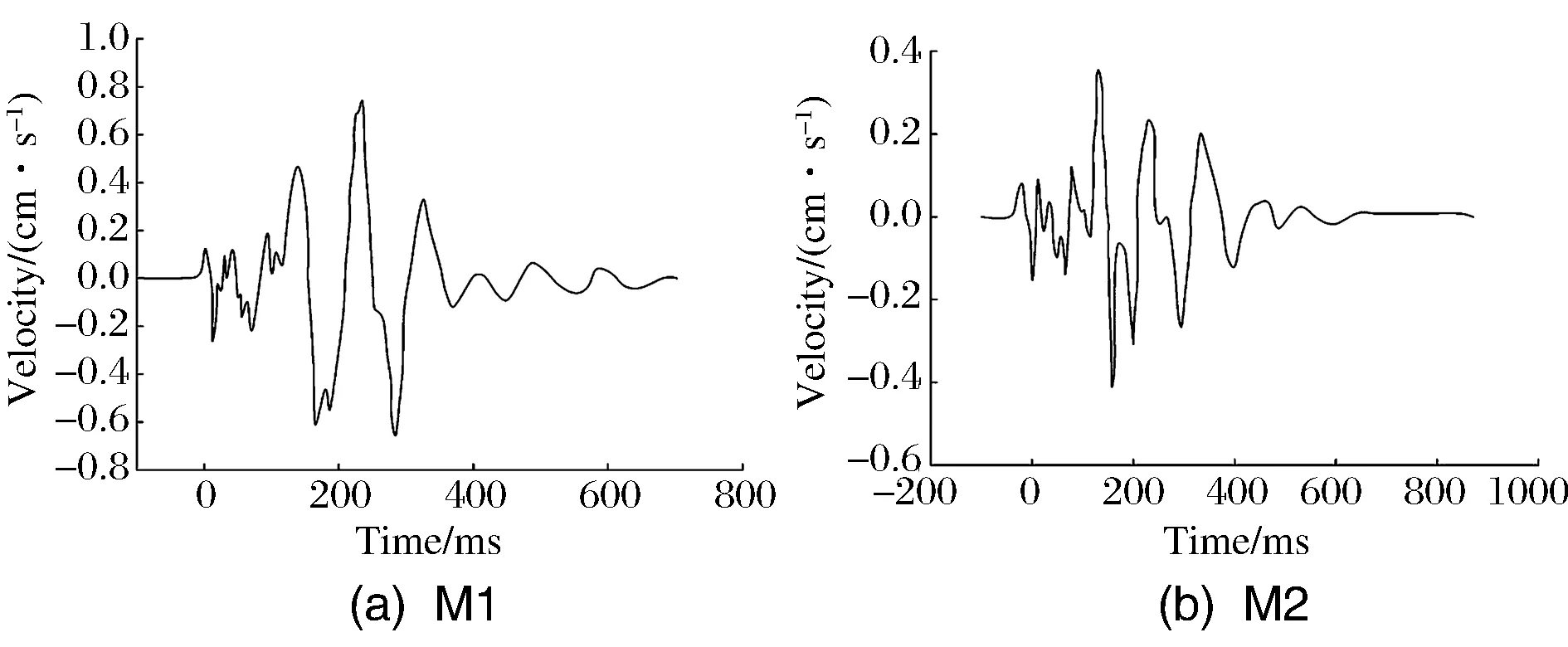
圖5　實測波形Fig.5　Measured waveform

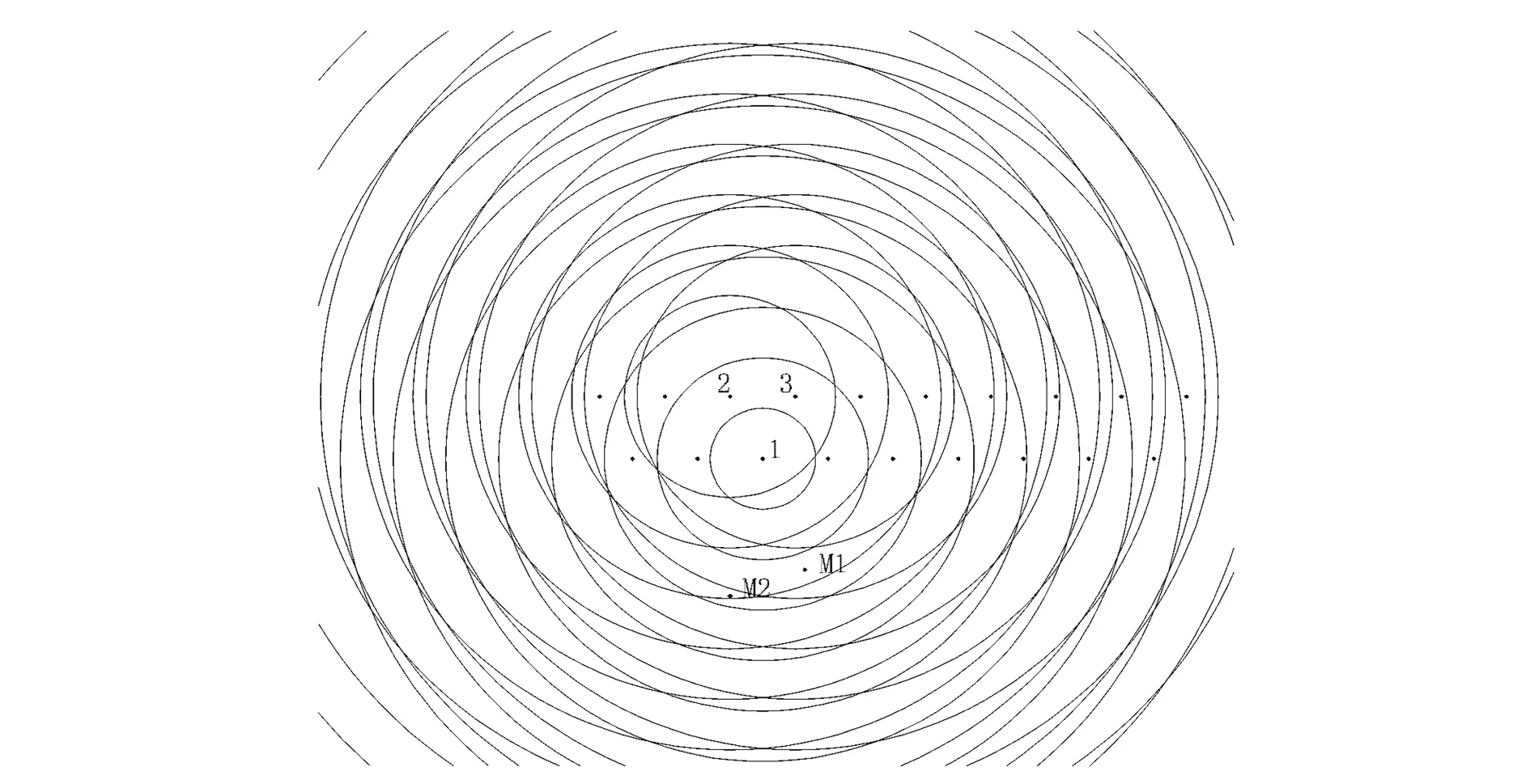
圖6　孔間延時間隔18 ms時爆破振動峰值預測結果Fig.6　Blasting peak vibration velocity prediction result at 18 ms hole delay time

模型預測峰值對比見表1。

表1中給出了預測速度峰值和實測速度峰值，可以看出，M1點正向速度預測峰值和實測速度峰值差距較小，M1點負向預測值和M2點預測值與實測值在誤差較大，但總體平均誤差在20%左右，其預測模型預測值具有一定的可信度。

孔間延時間隔12，9，7，4ms時爆破振動峰值預測結果分別如圖7～圖10所示。在圖7中M1點和M2點到波源1、2、3所形成波陣面法向距離不相等，因此在之后的某一個時刻，受到波源的共同影響；在圖8中，中M1點和M2點到波源1、2、3所形成波前鋒面法向距離不相等，因此在之后的某一個時刻，受到波源的共同影響；在圖9中〔9〕，M1點在波源1波陣面上，因此主要受到波源1的影響，由此可以計算出其位置處的速度峰值大小，同樣M2點也在波源1波前鋒面上，從而可以計算其振動速度峰值大小；在圖10中，M1點到波源1、2、3所形成波前鋒面法向距離不相等，因此在之后的某一個時刻，受到波源的共同影響，M2點分別在波源2的波前鋒面上，因此主要受到波源的影響，由此可以計算出其速度峰值大小。

表1　模型預測峰值對比

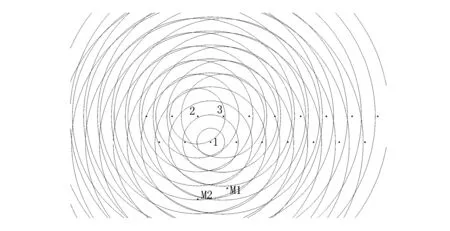
圖7　孔間延時間隔12 ms時爆破振動峰值預測結果Fig.7　Blasting peak vibration velocity prediction result at 12 ms hole delay time

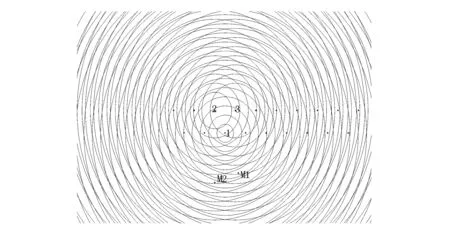
圖8　孔間延時間隔9 ms時爆破振動峰值預測結果Fig.8　Blasting peak vibration velocity prediction result at 9 ms hole delay time

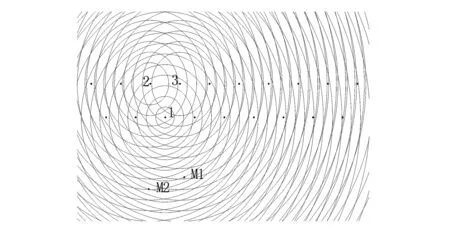
圖9　孔間延時間隔7 ms時爆破振動峰值預測結果Fig.9　Blasting peak vibration velocity prediction result at 7 ms hole delay time

不同毫秒延時間隔預測速度峰值見表2。

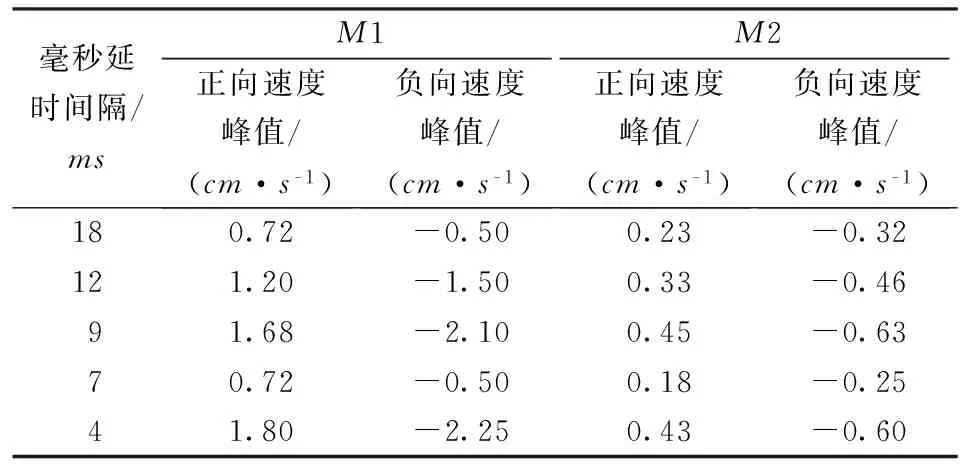
表2　不同毫秒延時間隔預測速度峰值

圖10　孔間延時間隔4 ms時爆破振動峰值預測結果Fig.10　Blasting peak vibration velocity prediction result at 4 ms hole delay time

從表2中可以看出，在毫秒延時間隔為12ms時的振動速度峰值要大于毫秒延時間隔18ms時的振動速度峰值；在毫秒延時間隔為9ms情況下，其產生的振動速度峰值要小于毫秒延時間隔為4ms時，但遠大于其他三種情況；毫秒延時間隔為4ms時振動速度峰值預測值較大；在毫秒延時間隔為7ms時M1點速度峰值和18ms較為接近，M2點速度峰值較小；從不同毫秒延時間隔的預測模型圖中，可以看出不同毫秒延時間隔對波形之間相互干涉作用，可以看出其增強和減弱的所在區域。

3結論

通過和實際工程中爆破振動峰值對比，建立的爆破振動峰值預測模型的誤差在20%左右。爆破振動參數的預報分析不僅局限于振動峰值速度，同時給出了一個爆破區域范圍內任意一點的爆破振動峰值增強和減弱所在的區域，并能根據需要保護的區域，來選取合理的毫秒延時間隔。精確延時爆破振動峰值預測模型在工程實際應用中不必選用經驗系數，避免了人為因素影響，工程可行性更強，便于在實際工程中推廣。

參考文獻(References)：

〔1〕 易長平，馮林，王剛，等. 爆破振動預測研究綜述[J]. 現代礦業,2011,27(5):1-5.

YIChang-ping，FENGLin，WANGGang，etal.Summaryofblastingvibrationprediction[J].ModernMining,2011，27(5):1-5.

〔2〕SINGBTN.Artificialneuralnetworkapproachforpredictionandcontrolofgroundvibrationinmines[J].MiningTechnology,2004,14(4):251-256.

〔3〕 徐全軍,劉強,聶渝軍,等. 爆破地震峰值預報神經網絡研究[J]. 爆炸與沖擊，1999,19(2)：38-43.

XUQuan-jun,LIUQiang,NIEYu-jun,etal.Studyofneuralnetworkpredictiononpeakparticleamplitudeofblastinggroundvibration[J].ExplosionandShockWaves, 1999,19(2):38-43.

〔4〕 言志信，言涅，江平，等.爆破振動峰值速度預報方法探討[J].振動與沖擊.2010，29(5):179-182.

YANZhi-xin,YANNie,JIANGPing，etal.Predictionmethodsforblasting-inducedgroundvibrationvelocity[J].JournalofVibrationandShock, 2010，29(5):179-182.

〔5〕 趙華兵，龍源，劉好全，等. 城市隧道爆破振動速度峰值預測神經網絡法應用[J]. 工程爆破，2014,20(5)：23-27.

ZHAOHua-bing,LONGYuan,LIUHao-quan,etal.Applicationofneuralnetworktopredictionofpeakamplitudeofblastingvibrationvelocityofurbantunnel[J].EngineeringBlasting,2014,20(5):23-27.

〔6〕 張藝峰，姚道平，謝志招. 基于BP神經網絡的爆破振動峰值及主頻預測[J]. 工程地球物理學報，2008，5(2):222-226.

ZHANGYi-feng,YAODao-ping,XIEZhi-zhao.Thepredictionofblastingvibrationpeakvalue&mainfrequencybyBPneuralnetwork[J].ChineseJournalofEngineeringGeophysics,2008，5(2):222-226.

〔7〕 文建華，李新平，張文成，等. 復合遺傳算法在爆破震動測試參數確定中的研究[J]. 巖土力學，2005,26(1):160-162.

WENJian-hua,LIXin-ping,ZHANGWen-cheng,etal.Astudyofparameterinversionofblastingvibrationbasedoncompositelygeneticalgorithm[J].RockandSoilMechanic, 2005，26(1):160-162.

〔8〕 史秀志，董凱程，邱賢陽，等. 基于支持向量機回歸爆破振動速度預測分析[J]. 工程爆破，2009,28(7):28-30.

SHIXiu-zhi,DONGKai-cheng,QIUXian-yang，etal.Analysisoftheppvpredictionofblastingvibrationbasedonsupportvectormachineregression[J].EngineeringBlasting, 2009,28(7):28-30.

〔9〕 楊年華,張樂. 爆破振動波疊加數值預測方法[J]. 爆炸與沖擊,2012,32(1):84-91.

YANGNian-hua,ZHANGLe.Blastingvibrationwaveformpredictionmethodbasedonsuperpositionprinciple[J].ExplosionandShockWaves,2012,32(1):84-91.

文章編號：1006-7051(2016)03-0079-04

收稿日期：2015-11-20

作者簡介：李順波(1985-)，男，博士，從事巖石爆破理論方面的工作。 E-mail： lshunbo@126.com

中圖分類號：TD235.4+7

文獻標識碼：A

doi：10.3969/j.issn.1006-7051.2016.03.017

Peakvibrationvelocitypredictionmodelofprecisiondelayblasting

LIShun-bo1,YANGRen-shu1,YANGJun2

(1.SchoolofMechanic&CivilEngineering，ChinaUniversityofMining&Technology(Beijing)，Beijing100083，China；2.StateKeyLaboratoryofExplosionScienceandTechnology，BeijingInstituteofTechnology，Beijing100081，China)

ABSTRACT：According to the basic principle of geometric seismology, with single hole blasting peak vibration velocity as basis and in accordance with the millisecond delay interval,the peak vibration velocity model of precision delay blasing with hole by hole was established.The results showed that the developed method could be used to predict the blasting vibration velocity peaks, it also could intuitively show the variation of blasting peak vibration velocity in the region and reasonable millisecond delay interval was set from the peak in protection region. The calculated velocity was coincident with the recorded ones in the deep hole blasting tests using electronic detonators. It indicated that the developed predication method was reliable for engineering applications.

KEY WORDS:Precision delay； Blasting vibration； Prediction model; Peak vibration velocity