K-GM(1，1)模型在巖體變形監測中的應用

馬符訊，席瑞杰，徐　南

(1.武漢大學 衛星導航定位技術研究中心，湖北 武漢 430079；2.武漢大學 測繪學院，湖北 武漢 430079；3.清華大學 地球系統科學研究中心，北京 100084)

?

K-GM(1，1)模型在巖體變形監測中的應用

馬符訊1，席瑞杰2，徐南3

(1.武漢大學 衛星導航定位技術研究中心，湖北 武漢 430079；2.武漢大學 測繪學院，湖北 武漢 430079；3.清華大學 地球系統科學研究中心，北京 100084)

摘要：傳統GM(1，1)模型存在著長期預測效果差、模型精度不高等問題，卡爾曼濾波能夠排除建模過程中隨機干擾因素，濾波值能夠反映更真實的數據情況。為了能更好地提高變形監測的預測精度，基于傳統GM(1，1)模型和卡爾曼濾波，提出K-GM(1，1)模型，利用該模型對巖體變形監測數據進行建模預測，并與傳統GM(1，1)模型預測結果進行對比分析，結果表明，K-GM(1，1)模型具有較高的預測精度，可作為變形監測的一種新方法。

關鍵詞：卡爾曼濾波；GM(1，1)模型；預測；變形監測

1基于卡爾曼濾波的灰色模型

1.1傳統GM(1，1)模型

設某系統原始觀測序列：X(0)={x(0)(1),x(0)(2),x(0)(3),…,x(0)(n)}，X(0)一次累加生成X(1)序列：X(1)={x(1)(1),x(1)(2),x(1)(3),…,x(1)(n)}，其中

(1)

當X(1)={x(1)(1),x(1)(2),x(1)(3),…,x(1)(n)}是時間t的連續可微函數并滿足一階微分方程：

(2)

式中：參數a為發展系數，表征系統的發展走勢；參數b為灰色作用量，表征數據變化的關系。

則GM(1，1)的時間響應函數

(3)

最后通過累減得到預測值：

(4)

1.2K-GM(1,1)模型

卡爾曼濾波是一種通過對被提取信號有關的觀測量的算法估計得出所需信號的濾波方法。離散系統的卡爾曼濾波的動態方程和量測方程

(5)

(6)

式中：xk,ωk-1分別為k時刻的狀態變量和動態噪聲;φk,k-1為k-1時刻到k時刻的狀態轉移矩陣；zk,Hk,vk分別為k時刻的觀測向量、量測方程系數矩陣和量測噪聲。

離散線性系統的狀態估計問題本質上就是根據觀測向量z1,z2,…,zk的數學模型，求得第tj時刻的狀態向量xk最優估值的問題，一般分為3種情況：

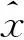
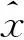
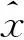
卡爾曼濾波過程的求解結果為

(7)

(8)

其中

Jk=

變形監測工程中，通常影響因素較多且相對復

雜，變形時間序列中不僅存在白噪聲，可能還存在著有色噪聲，從而產生建模誤差。本文構建的K-GM(1,1)模型，設定卡爾曼濾波過程的狀態參數為監測點的位移量及其位移速度，設定動態噪聲為監測點的位移加速度，故卡爾曼濾波動態方程為

式中：xk,vk,ak分別為監測點的位移量，位移速度和加速度;ωk-1為動態噪聲;tk-1表示時間。K-GM(1,1)模型處理流程如圖1所示。

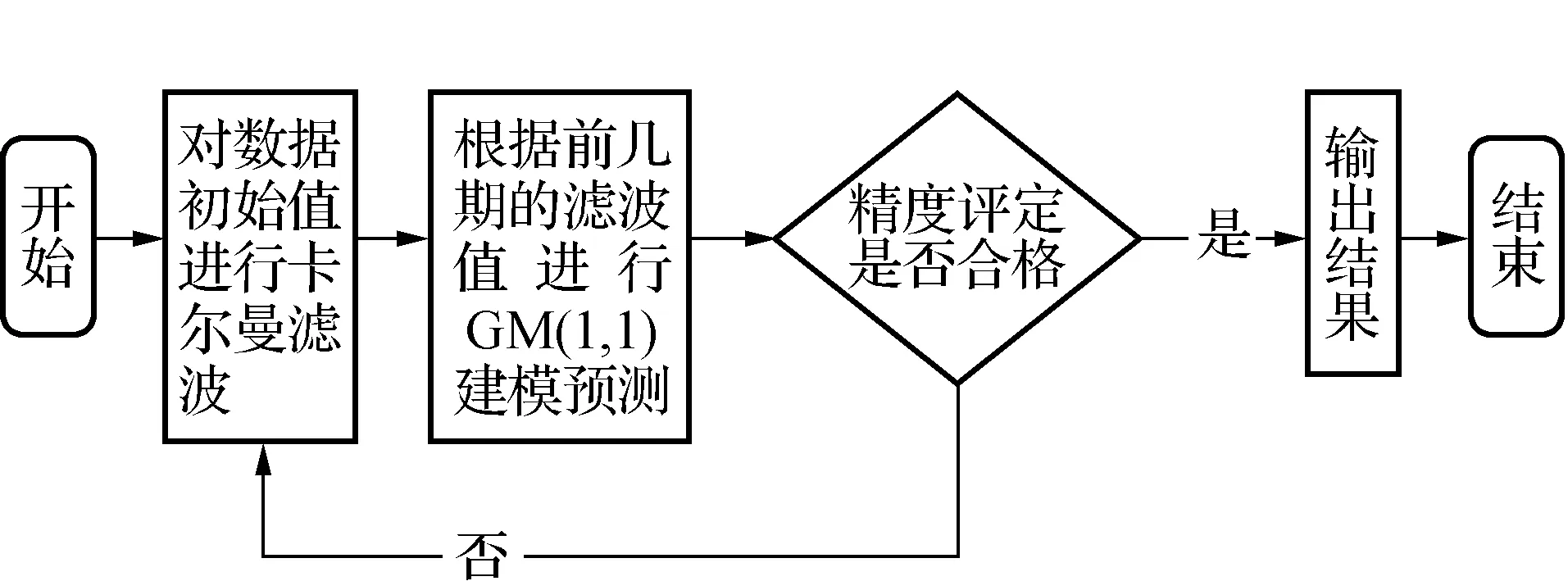
圖1　K-GM(1,1)模型處理流程

2工程實例

為保證隧道建成后洞口巖體的安全性，于2014年開始對其進行健康監測，監測周期為1個月，同時為驗證K-GM(1，1)模型的有效性，本文以某隧道出口洞頂巖體監測點2014年前11期的沉降監測值為例,如表1 所示，其中前5期的實測值為原始序列，試驗過程為首先利用卡爾曼濾波對其建模數據進行處理，剔除隨機擾動誤差的影響，再運用灰色理論對濾波值進行建模，并預測后6期的變形發展趨勢，最后計算實測值與預測結果的殘差，驗證模型的可靠性。

表1　某巖體監測點2014年前11期的沉降監測值

2.1傳統GM(1,1)模型預測

首先選取原始觀測序列的前5期進行建模，再利用傳統的GM(1,1)模型對后6期數據進行預測，通過計算求得原始觀測值和預測值的殘差，對預測結果進行評估。傳統GM(1,1)模型預測結果如表2所示。

由表2可以看出，傳統的GM(1,1)模型預測精度總體良好，但存在隨預測時間增加，預測精度下降的情況，傳統的GM(1,1)模型在長期預測方面模型的預測精度不能得到很好的保證，不能反映巖體最真實的變形規律和變形趨勢。

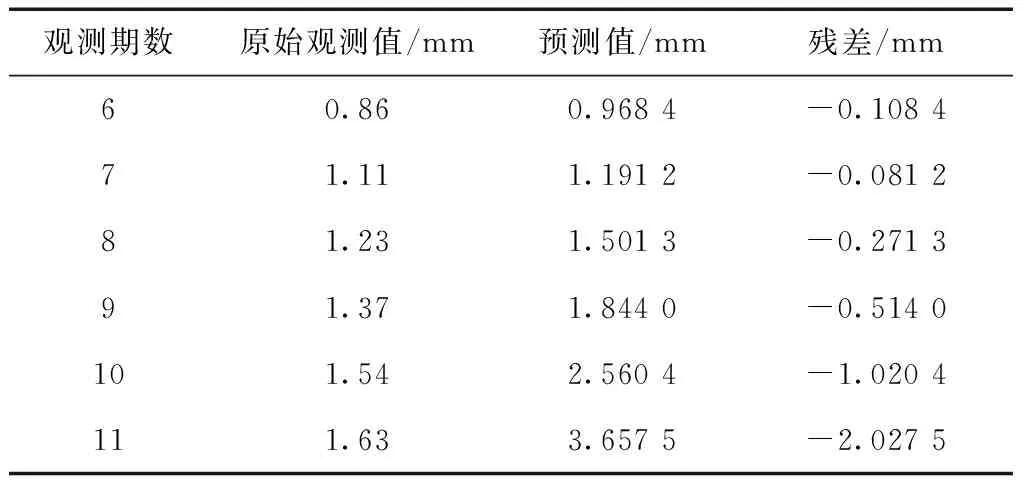
表2　傳統GM(1,1)模型預測

2.2K-GM(1,1)模型預測

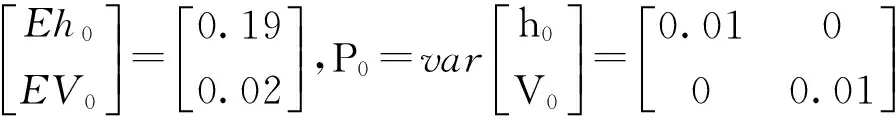
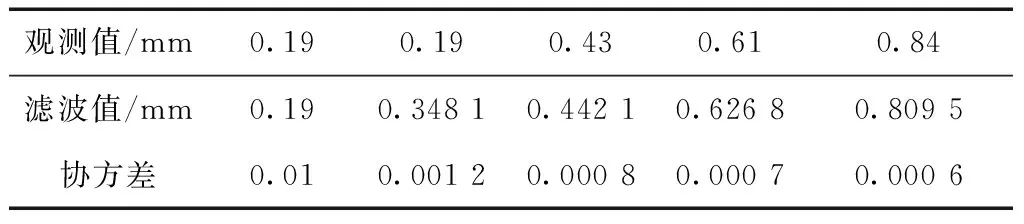
表3　原始序列的卡爾曼濾波結果

由表3可以看出，濾波值由第二期開始收斂，協方差基本也穩定在0.001以內，同時其變化趨勢為越來越小，逐漸趨近于0。在此基礎上，本文再利用傳統GM(1,1)模型對前5期的卡爾曼濾波值進行建模預測，后6期的預測結果如表4所示。

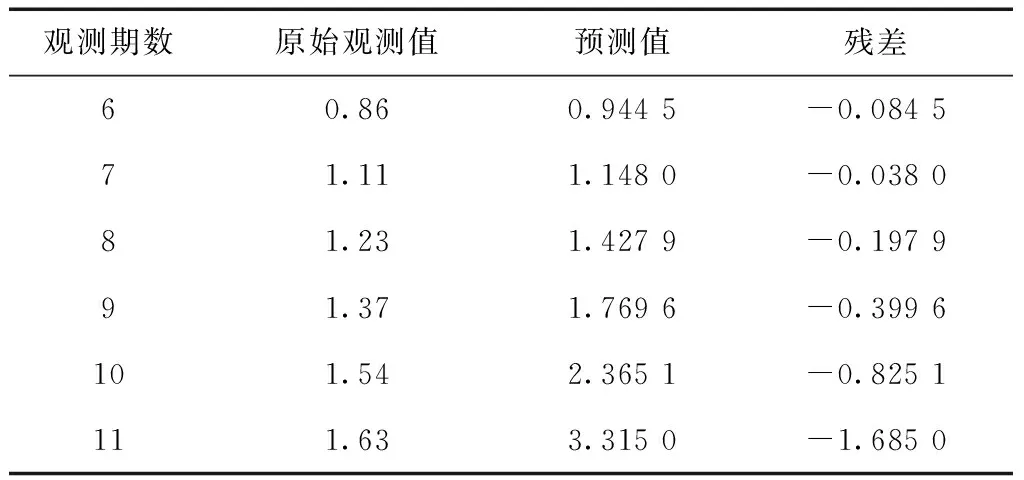
表4　K-GM(1,1)模型預測　mm

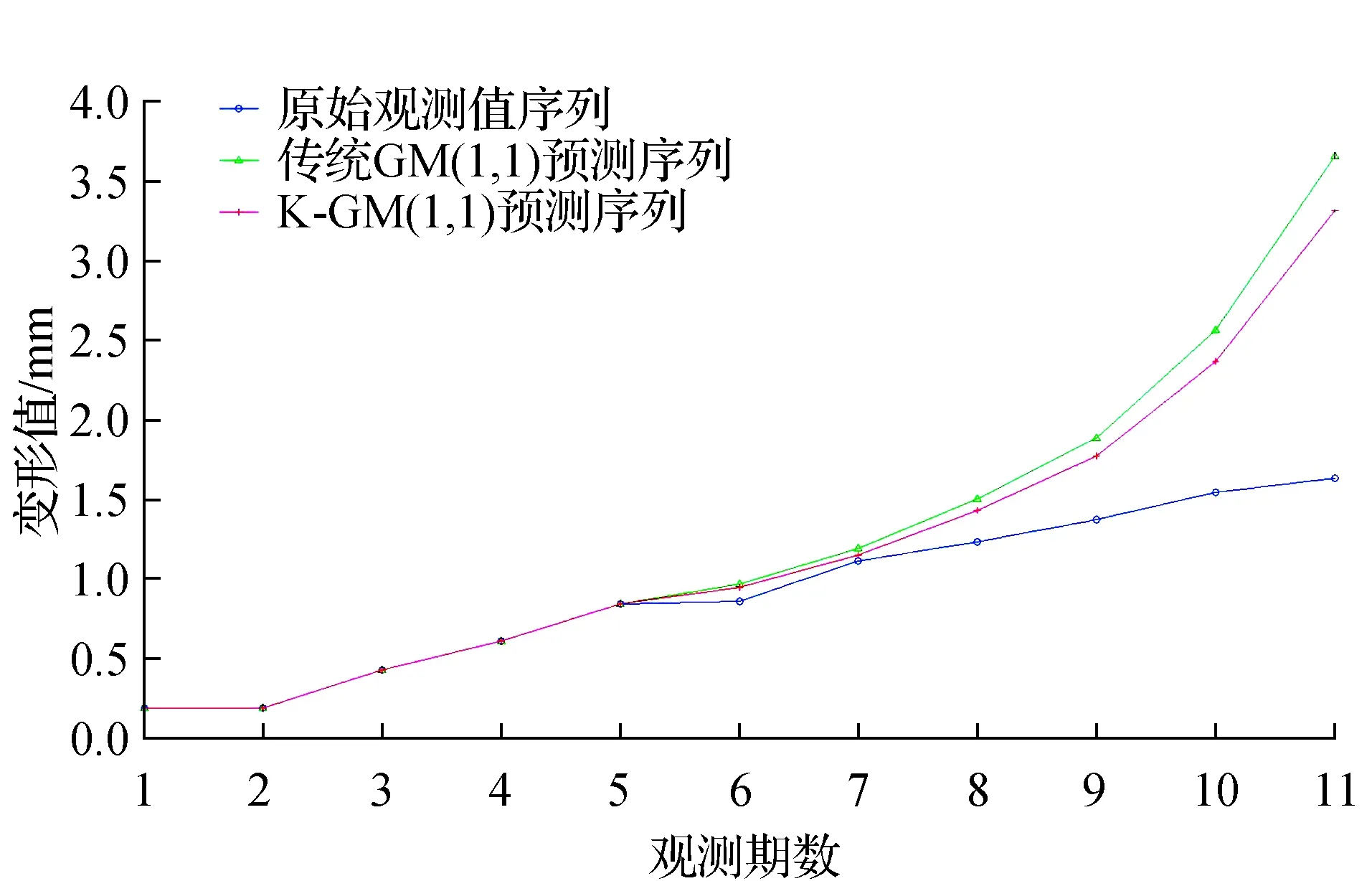
圖2　K-GM(1,1)模型與傳統GM(1,1)模型預測值比較

圖2所示為傳統GM(1,1)模型與K-GM(1,1)模型預測值對比結果，從圖2中可以看出，K-GM(1,1)模型預測精度總體良好，優于傳統GM(1,1)模型的預測精度，但隨著預測時間的增加，該模型也呈現了預測精度下降的趨勢，這與GM(1,1)的模型特點有關，卡爾曼濾波的作用只是剔除建模數據中的干擾因素，并不能排除預測過程中的誤差源。K-GM(1,1)模型的預測值相比傳統GM(1,1)模型更接近真實的變形值。因此，經過改進K-GM(1,1)模型可以更好的反映巖體的變形規律和變形趨勢。

3結論

本文利用卡爾曼濾波和傳統GM(1,1)模型構造出K-GM(1,1)模型，利用該模型對巖體變形數據進行分析預測，并與傳統GM(1,1)模型的預測結果進行對比分析，結論：K-GM(1，1)模型的預測精度優于傳統的GM(1，1)模型，但依然存在著長期預測精度低的問題，這與傳統GM(1,1)的模型原理有關，今后可引入自適應動態調節因子，建立動態GM(1,1)模型解決該問題。總之，本文提出的K-GM(1,1)模型程序實現簡單，預測精度高，具有更好的預測效果，故K-GM(1，1)模型在巖體變形預測中具有較高的應用價值。

參考文獻：

[1]鄧聚龍.灰色系統基本方法[M].湖北：華中工學院出版社,1987.

[2]李日云,王利,張雙成.灰色預測模型在高層建筑物沉降預測中的應用研究[J].地球科學與環境學報,2005,27(1)：23-26.

[3]甘月云,陳星,付軍,等.基于灰色預測GM(1，1)模型的城鎮生活需水量預測[J].水電能源科學，2012(9):40-42.

[4]劉思峰，黨耀國，方志耕，等.灰色系統理論及其應用[M].北京：科學出版社，2010.

[5]喜文飛,史正濤.基于卡爾曼濾波的動態灰色理論模型研究[J].測繪工程,2014,23(3):24-27.

[6]吳彥,張鐸強,徐南.反向灰色模型的初值優化在道路沉降中應用[J].測繪工程,2014,23(12)：60-62.

[7]INCE C D,SAHIN M.Real-time deformation monitoring with GPS and Kalman Filter[J].Earth Planets and Space,2000,52(10)：837-840.

[8]王琦,孫華,李偉華，等.卡爾曼濾波在變形監測數據處理中的應用[J].工程地球物理學報,2009,6(5):658-661.

[9]文鴻雁,周呂,韓亞坤，等.基于卡爾曼濾波的GM(1,1)模型在高鐵隧道沉降變形分析中的應用[J].大地測量與地球動力學,2014,34(1):88-91.

[10] 任遠軍，李龍，石寧，等.改進的 GM(1，1) 模型在大壩變形預測中的應用[J].測繪工程，2015,24(6)：61-64.

[11] 姜剛,楊志強,張貴鋼.卡爾曼濾波算法的灰色理論模型在變形監測中的應用[J].測繪科學,2011,36(4):19-21.

[責任編輯：李銘娜]

DOI:10.19349/j.cnki.issn1006-7949.2016.08.010

收稿日期：2015-05-07；修回日期：2015-06-25

基金項目：國家自然科學基金資助項目(41374033)

作者簡介：馬符訊(1992-)，男，碩士研究生.

中圖分類號：F291.1

文獻標識碼：A

文章編號：1006-7949(2016)08-0042-03

Application of K-GM(1，1)model to the deformation monitoring of rocks

MA Fuxun1，XI Ruijie2，XU Nan3

(1.Research Center of GNSS,Wuhan University,Wuhan 430079,China；2.School of Geodesy and Geomatics,Wuhan University,Wuhan 430079,China；3.Center of Earth System Sciences，Tsinghua University,Beijing 100084,China)

Abstract：There are some problems in the tradition GM(1,1) forecast models such as the bad effect in the long term prediction and the low accuracy and so on.Therefore,Kalman filter method has the advantage of eliminating random interference factors in the process of modeling,and the filtered data can reflect the real situation of the project.In order to improve the prediction accuracy of deformation monitoring,this paper proposes to use the K-GM (1,1) model,based on the GM (1,1) model and Kalman filter,and to analyze the rock mass deformation monitoring data.The results indicate that comparing with the GM(1,1) model,the K-GM(1,1) model can achieve a higher prediction accuracy,which can be used as a new method for deformation monitoring.

Key words：Kalman filtering;GM(1，1)；forecast；deformation monitoring