一種改進的永磁交流伺服系統滑模控制器設計＊

2016-07-07 08:23:59郭小定

電氣傳動自動化 2016年2期

王　興，郭小定，柏　達，范　婷

（湖南科技大學信息與電氣工程學院，湖南湘潭411201）

王興，郭小定，柏達，范婷

（湖南科技大學信息與電氣工程學院，湖南湘潭411201）

摘要：針對傳統整數階PID伺服控制精度低、魯棒性差等問題，結合滑模控制、分數階理論、和神經網絡參數整定技術各自的優點，提出了一種分數階神經滑模控制的控制策略。首先對PMSM伺服系統的結構模型和數學模型進行了詳細的闡述。然后利用滑模控制和等效控制理論設計了一種新的分數階滑模控制器，提高了其綜合性能。最后利用神經網絡的強學習能力對分數階滑模控制率參數進行了有效整定。實驗結果表明，此分數階神經滑模控制策略魯棒性強、響應速度快、定位精度高，能有效消除抖振，具有良好的綜合性能。

關鍵詞：PMSM；伺服系統；滑模控制；分數階；神經網絡；魯棒性

1　引言

隨著微電子、計算機、電力半導體和電機制造技術的巨大進步，交流伺服控制技術日益成熟，應用日益廣泛，特別是交流永磁伺服控制技術。目前伺服控制系統普遍采用的仍然是傳統的PID控制方法，但由于永磁同步電動機（PMSM）自身具有一定的非線性、強耦合性和時變性等特點，且其伺服對象也存在較強的不確定性和非線性，加之系統運行時還會受到不同程度的干擾，因此，按照常規控制策略很難滿足高性能永磁同步電動機伺服控制系統的控制要求，需要引進一種有效的控制技術使系統在復雜條件下仍能保持良好的伺服性能。

滑模變結構控制最突出的優點是系統一旦進入滑模運動狀態，其對系統的擾動及參數變化就具有完全的魯棒性，其對控制對象的模型精度要求不高，目前正被逐步引入到伺服電機控制系統中［1］，但滑模控制系統的抖震問題限制了其在實際工程中的廣泛應用。針對傳統滑模變結構控制系統中的抖振問題，把分數階微積分理論引入到滑模控制方法中，并結合神經網絡學習能力進行參數整定，有效消除抖振，同時提高其綜合性能，提出了一種神經網絡分數階滑模控制策略。

2　交流伺服系統結構及數學模型分析

2．1伺服系統結構分析

基于永磁同步電機及其驅動器的交流伺服運動控制系統結構圖如圖1所示，圖中驅動部分的伺服電機和驅動器外加編碼器構成了通常所說的伺服系統，而伺服運動控制系統具有更加廣泛的含義，除了驅動部分外，還包括操作軟件、控制部分、檢測元件、傳動機構和機械本體，各部件協調完成特定的運動軌跡或工藝過程［2］。

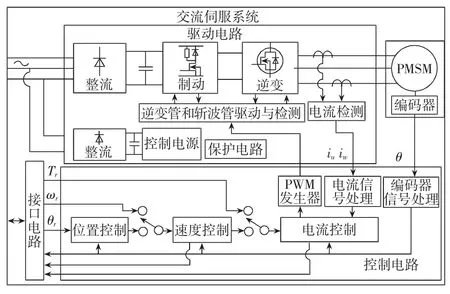
圖1　交流伺服系統控制結構圖

在三環結構中，電流環和速度環為內環，位置環為外環。三環結構可以使伺服系統獲得較好的動態跟蹤性能和抗干擾性能。其中，電流環的作用是改造內環控制對象的傳遞函數，提高系統的快速性，及時抑制電流環內部的干擾，并限制最大電流，使系統具有足夠大的加速扭矩，保障系統安全運行。速度環可以增強系統抗負載干擾的能力，抑制速度波動。位置環的作用是保證系統靜態精度和動態跟蹤性能，使整個伺服系統穩定高效運行。運動系統中一般是對伺服系統的速度環和位置環進行研究［2-3］，本文也是基于這兩個環進行研究和設計。

2．2數學模型分析

PMSM的運動方程為：

由式（1）可得：

J為轉動慣量（kg·m2），TL為負載轉矩，β為粘滯摩擦系數，ωr為轉子機械角速度，Te為電磁轉矩（N·m）。

PMSM電磁轉矩的方程為：

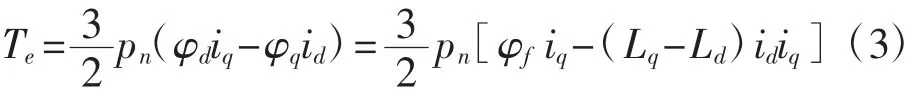
其中，φf為轉子上的永磁體產生的磁勢，φf＝ifLmd，φd、φq為dq軸的定子磁鏈，Ld、Lq為dq軸的定子電感。

通過應用矢量控制原理［2］，電磁轉矩方程可以簡化成：

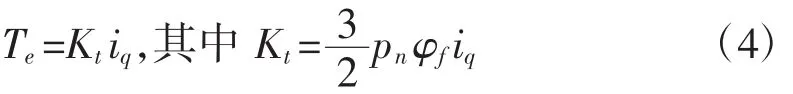
Kt為功率驅動電路的放大系數，iq為電流控制信號，pn為極對數。將式（4）代入式（2）可得：

如果考慮電機的參數變化，上式可表示為：

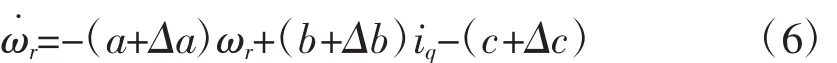
其中，Δa、Δb、Δc為系統的參數擾動值。控制器的設計目的是找到合適的控制率，使系統的輸出角θ快速跟蹤輸入角θr。

3　分數階滑模控制器的設計

分數階滑模控制器的設計分為兩步：滑模面的設計和滑模控制律的設計［4］。

分數階切換函數選擇為：

其中，0＜r＜1，c∈R+。

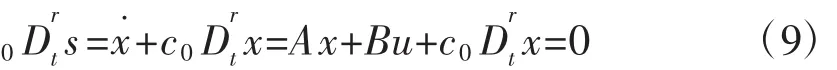
則等效控制ueq為：

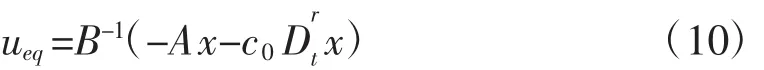
為了保證滑模到達條件成立，設計切換控制如下：

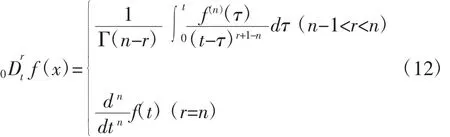
滑模控制率由等效控制項和切換控制項組成，即：

4　神經網絡整定開關增益

滑模控制器中的開關增益η對伺服系統的控制性能影響很大，抖振問題一直是滑模控制理論研究中難以解決的問題，究其原因主要是由于控制器的不連續切換項造成的，如果系統切換增益η太大，則系統的抖振變大，影響系統的控制精度；反之，如果切換增益η太小，則系統不能達到切換流型。因此，選擇合適的方法，適當減小切換項增益，可有效消除抖振。本文采用一種學習能力強的神經網絡算法來整定開關增益η。

神經網絡輸入輸出算法為［9］：

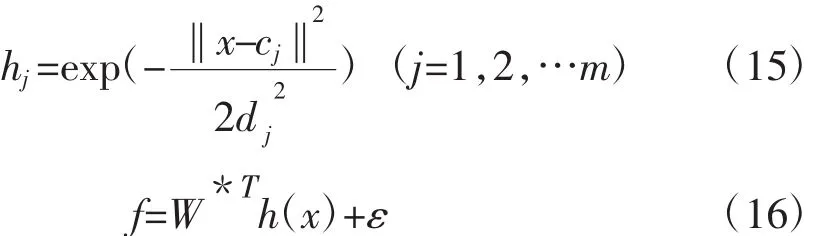
hj為高斯函數，h＝［h1，h2，…hm，］T為高斯基函數的輸出，x為網絡輸入向量，cj＝［cj1，cj2，…cjn，］T為第j個節點的中心矢量，bj為j節點的基寬度參數（大于零），W＊為理想網絡權值，ε為網絡的逼近誤差（為很小的正實數），f為網絡輸出。

設網絡的權值向量為W＝［w1，w2，…wm］T，則網絡的辨識輸出為：

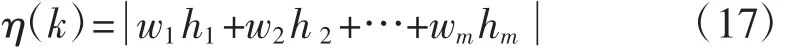
定義神經網絡的兩個輸入量：x1＝（sk），x2＝（sk）。選擇神經網絡的整定指標為：

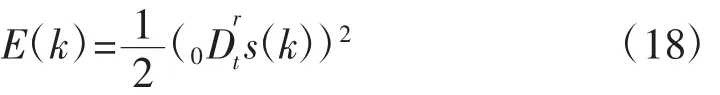
由式（9）可得：

根據梯度下降法，輸出權值的網絡學習迭代算法表示為：

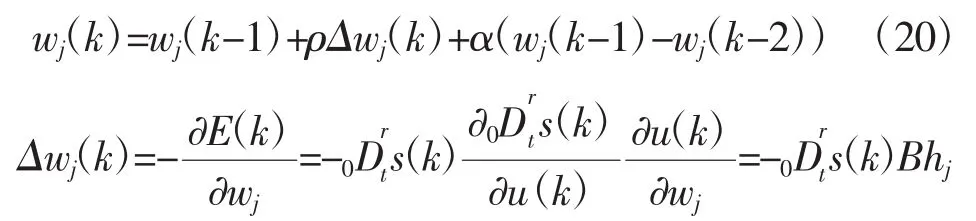
式中ρ為學習速率，α為動量因子。

節點基寬參數的迭代算法為：

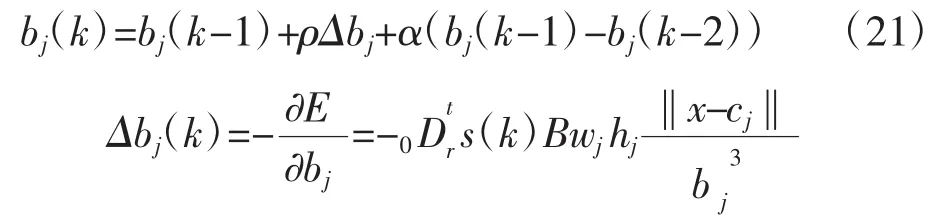
節點中心迭代算法為：

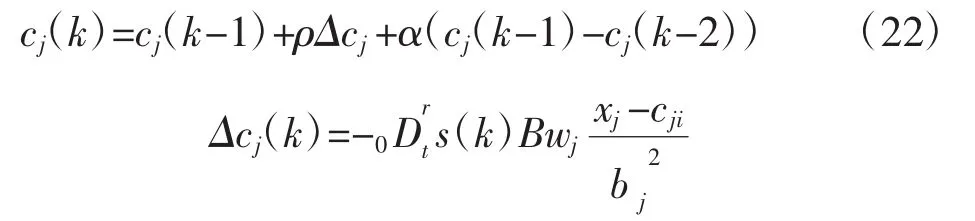
根據上述迭代算法［10］，可以整定出合適的開關切換增益系數η，從而使系統滿足需求的控制性能。

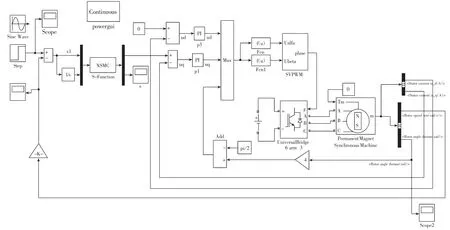
圖2　改進的PMSM滑模控制的伺服系統仿真模型

5　仿真結果與分析

為檢驗以上所設計的伺服控制策略的性能及其合理性，在永磁同步電機伺服系統結構基礎上，以Matlab為仿真工具，在Simulink中搭建了仿真模型如圖2所示，其中XSMC模塊為分數階神經滑模控制模塊。然后，分別對系統的階躍響應和正弦響應進行了仿真分析［11、12］。

設置永磁同步電機的主要參數為：Ld＝Lq＝8．0e-3H，pn＝2，J＝4．5e-4kg·m2，β＝1．0e-3N·m·s，定子電阻為2Ω，額定轉速為1500r／min，額定功率為2kW，額定轉矩為6．45N·m。滑模函數中取r＝0．5、c＝25，輸入指令取θr（t）＝0．1sin（1．42πt），選擇神經參數ρ＝0．6，α＝0．05，高斯函數參數初始值取網絡權值的初始值為w＝［0．1，0．1，0．1，0．1，0．1］。

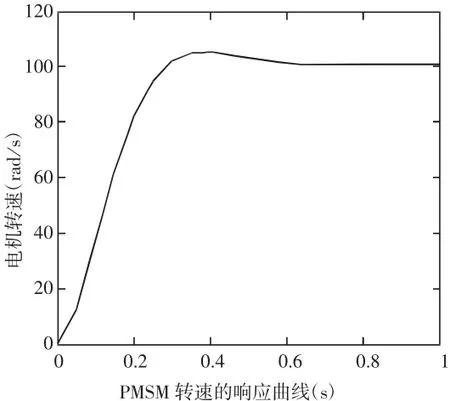
圖3　電機速度的階躍響應曲線

系統的速度階躍響應曲線如圖3所示，給定速度取100rad／s，從圖3可以看出，改進的系統速度響應快，且超調量小，速度無明顯波動，抗干擾能力強，具有較強的動態性能，符合系統的要求。接著在Matlab環境下，分別進行分數階神經網絡滑模控制器和傳統整數階PID（以一階為例）控制策略進行仿真對比分析，以正弦響應曲線為例，仿真結果如圖4和圖5所示。

圖4　分數階神經滑模控制位置和速度正弦響應曲線

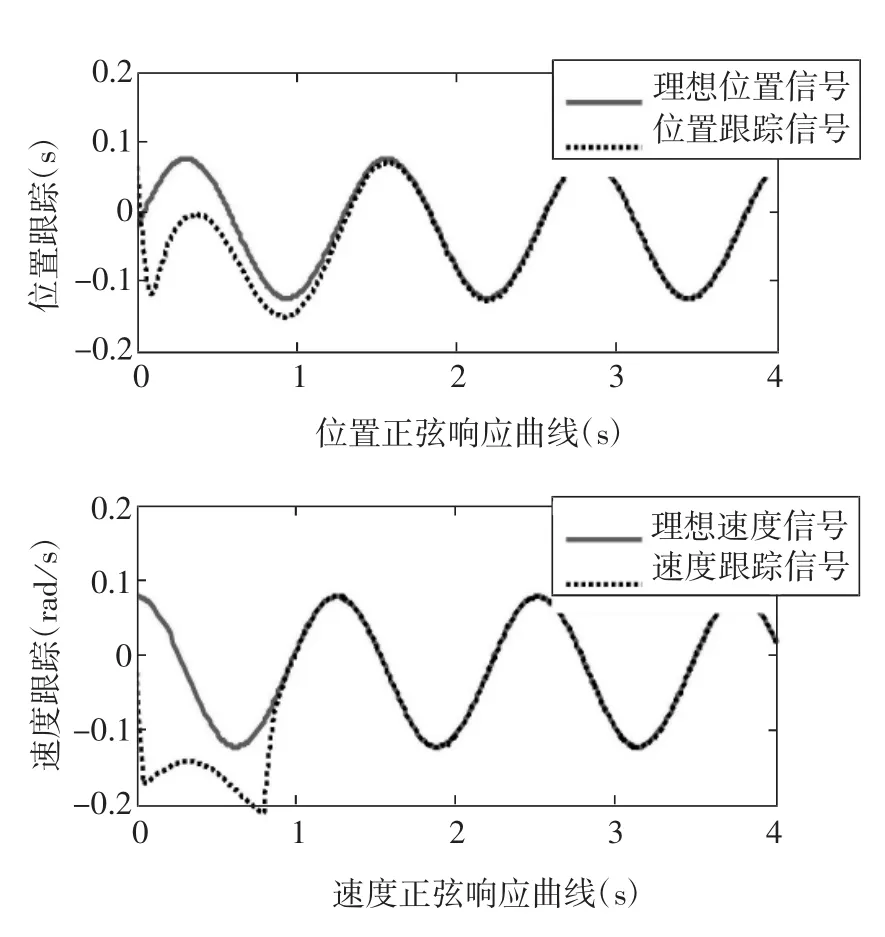
圖5　傳統PID控制的位置和速度正弦響應曲線

上圖分別給出了分數階神經網絡滑模控制策略和傳統PID控制策略（去掉圖2模型中的XSMC模塊）的仿真結果。從圖4和圖5可以看出，分數階神經網絡控制響應速度快，無論位置和速度響應時間都小于0．5s，甚至更快。它能以最快的加速度加速到額定速度，定位精度高，具有更好的正弦跟蹤性能，對滑模參數能夠進行整定，能夠有效消減系統的抖振，系統運行穩定且魯棒性強。而傳統PID控制方法的響應時間相對較長，前期跟蹤精度差，會出現明顯偏差，這在如今高性能的伺服領域是不允許的。從上述幾幅圖中可以知道，分數階神經滑模控制策略不但能有效削減系統自身抖振，還能達到比傳統PID控制系統更好的綜合控制性能，充分證明了其可行性。

6　結束語

本文針對傳統伺服控制策略出現的缺點與不足，結合滑模控制、分數階理論和神經網絡參數整定技術各自的優點，完成了對PMSM交流伺服系統的一種改進型分數階神經滑模控制器的設計。本文將分數階理論應用到滑模控制系統中，采用等效控制的組合方式設計控制器的控制率，利用神經網絡對其開環進行整定優化。永磁同步電機伺服系統仿真結果表明，本文所提出的改進型分數階神經滑模控制策略不但魯棒性強、抖振小，而且響應速度快、定位精度高，具有良好的綜合性能，能夠廣泛應用于實際工程實踐中。

參考文獻：

［1］方斯琛，周波．滑模控制的永磁同步電機伺服系統一體化設計［J］．中國電機工程學報，2009，29（3）：96-101．

［2］金鈺，胡佑德，等．伺服系統設計指導［M］．北京：北京理工大學出版社，2000．

［3］楊書生，鐘宜生．永磁同步電機轉速伺服系統魯棒控制器設計［J］．中國電機工程學報，2009，29（3）：84-90．

［4］胡躍明．變結構控制理論與應用［M］．北京：科學出版社，2003．

［5］薛定宇，趙春娜．分數階系統的分數階PID控制器設計［J］．控制理論與應用，2007，24（5）：771-776．

［6］Zhang J J，Chen X L，Feng R P，et al．Design of variable structure controller based on friction adaptive compensation ［J］．Journal of Harbin Institute of Technology，2000，32 （4）：92-95．

［7］曾慶山，曹廣益．分數階線性系統的能觀性研究［J］．系統工程與電子技術，2004，26（11）：1647-1650．

［8］曾慶山，曹廣益，朱新堅．分數階控制系統的仿真方法［J］．計算機仿真，2004，21（2）：84-86．

［9］LU Ying -wei，Sundararajan，Saratchandran．Performance evaluation of a sequential minimal radial basis function neural network learning algorithm［J］．IEEE Transactions on Neural Networks，1998，9（2）：308-318．

［10］劉治鋼，王軍政，趙江波．永磁同步電機神經網絡自適應滑模控制器設計［J］．電機與控制學報，2009，13（2）：290-295．

［11］汪海波，周波，方斯琛．永磁同步電機調速系統的滑模控制［J］．電工技術學報，2009，29（9）：71-77．

［12］劉金琨．滑模變結構控制MATLAB仿真［J］．北京：清華大學出版社，2005．

Design of modified sliding-mode controller for permanent magnet AC servo system

WANG Xing，GUO Xiao-ding，BAI Da，FAN Ting

（School of Information and Electrical Engineering，Hunan University of Science and Technology，Xiangtan 411201，China）

Key words：PMSM；servo system；sliding mode control；fractional order；neural network；robustness

Abstract：In view of the traditional integer order PID servo control with low precision and poor robustness，combining with the respective advantages of the sliding mode control，the fractional theory and the neural network parameter setting，a neural sliding mode fractional order control strategy is proposed．Firstly，the full-digital fuzzy servo system structure model and mathematical model have been detailed，then the design of a new kind of fractional order sliding mode controller by using of the sliding mode control and equivalent control theory for improving the comprehensive performance is presented，and finally the parameters setting of the fractional order sliding mode control using the strong learning ability of the neural network is given．The experimental results show that this fractional order neural sliding mode control strategy enables the system of strong robustness，fast response and high positioning accuracy，and can effectively eliminate the chattering and makes the system good comprehensive performance．

中圖分類號：TM351

文獻標識碼：A

文章編號：1005—7277（2016）02—0013—05

基金項目：＊國家自然科學基金資助項目（51577057）．

作者簡介：