強震作用下超高橋墩動力穩定性理論研究①

(1.延安大學建筑工程學院，陜西 延安 716000; 2.西安建筑科技大學土木工程學院,陜西 西安 710055)

強震作用下超高橋墩動力穩定性理論研究①

(1.延安大學建筑工程學院，陜西 延安 716000; 2.西安建筑科技大學土木工程學院,陜西 西安 710055)

摘要：根據平截面假定,考慮超高橋墩大位移變形產生的幾何非線性影響,建立超高橋墩的振動控制微分方程,利用變步長的龍格-庫塔法進行求解,結合B-R運動判定準則,對超高橋墩在地震作用下的動力失穩機理進行研究。理論分析表明,超高橋墩的動力失穩與橋墩的幾何尺寸、質量分布、邊界條件有密切關系;橋墩動力失穩時刻隨地震波加速度峰值的增大而減小;失穩時刻與失穩加速度荷載有對應關系。算例結果表明:本文方法正確,利用本文理論能夠準確計算超高橋墩的失穩時刻及失穩加速度,對超高橋墩動力失穩的理論分析及工程實踐有重要指導意義。

關鍵詞：強震作用; 超高橋墩; 動力穩定性; 位移形函數; 龍格-庫塔法

0引言

隨著西部大開發計劃的順利實施,在我國西南部建造了一大批超高橋墩橋梁。在地震動力荷載作用下,超高橋墩的性能失效往往由其動力穩定性控制,國內外已有對該類結構動力穩定性的研究[1-2]。但由于對結構進行動力分析時引入了時間參量,使得其動力穩定性分析變得極為困難,加之結構自身動力特性的復雜性,使得其難以用數學形式準確表達[3]。隨著力學理論的發展,關于結構動力穩定分析理論不斷豐富,如結構前屈狀態的研判、臨界荷載的確定、穩定準則的建立和結構動力失穩后結構的分析等。

孫強等[4-5]探討了彈性介質桿在軸向荷載作用下,阻尼力對桿件穩定性的影響規律,并推導了桿件在不同邊界條件下的動力分析計算公式。徐艷等[6]基于Liapunov運動穩定性定義,建立了兩類結構穩定狀態概念:第一類是彈性動力屈曲,通過動態特征值法進行分析研究;第二類是動力極值,利用B-R準則結合動態增量法(IDA)進行研究,其從動力穩定角度探討了鋼管混凝土拱橋的抗震性能。Bakker[7]研究了橫向均布荷載作用下圓柱體的動力穩定及前屈狀態。羅松南等[8-9]通過對高橋墩的簡化分析,建立墩頂簡支、墩底固結的壓桿模型,研究分析了該橋墩模型在地震荷載和軸向沖擊荷載作用下結構的動力屈曲。羅漪等[10]利用有限單元法研究了變剛度薄壁桿件在受軸向周期性作用下的動力穩定。盧皓等[11]和夏修身等[12]利用彈塑性分析方法對超高墩橋梁的高墩抗震性能及地震破壞機理進行了分析研究。李黎等[13-14]通過對結構動力分析原理進行剖析,利用有限元方法和動力特征值屈曲分析方法相結合,對設有隔震的橋梁進行了動力穩定性分析,分析結果表明該隔震橋梁動力穩定性能良好。除了在理論方面對結構動力穩定性的研究,國內外學者也通過試驗手段對軸向受力桿件進行了動力屈曲研究,如孫華東[15]通過試驗方法研究了圓管的軸向沖擊動力屈曲。

本文根據大位移理論,通過考慮超高橋墩變形的幾何非線性與結構內力的關系,建立了超高橋墩在彈性狀態下動力穩定計算的二階控制微分方程,結合變步長的Runge-kutta法研究了超高橋墩的動力響應。根據B-R判定準則,對超高橋墩在強震作用下結構的動力失穩破壞機理進行了研究分析。算例的數值計算結果表明,本文方法正確,根據本文理論能夠準確預測超高橋墩的失穩時刻及其對應的地震波加速度荷載。

1分析模型建立

根據超高橋墩受載變形的力學特性,將超高橋墩簡化為底端與地面固結,頂端設有集中質量和有限剛度側向支撐的均質彈性壓彎桿件,地震荷載通過與地面固結的墩底輸入。在地震荷載作用下,當超高橋墩發生失穩破壞時其常處于彈性受力狀態,即屬于小應變大位移的幾何非線性問題,因而在構件變形與內力分析時,假定壓彎桿件符合平截面假定。結合以上超高橋墩簡化模型和分析假定,超高橋墩動力分析模型如圖1所示。規定:桿件按圖1向左凸彎曲為正,軸力拉為正。

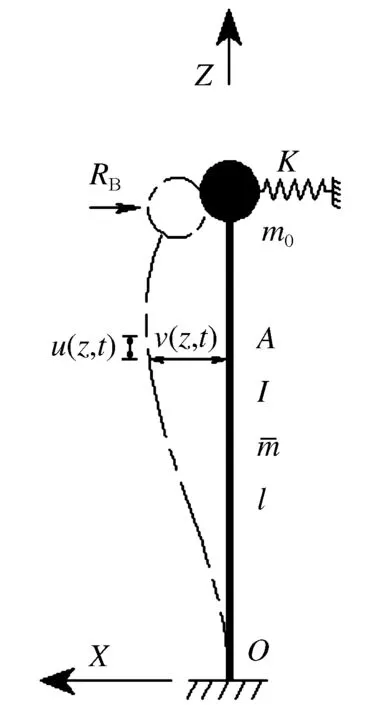
圖1　超高橋墩分析模型Fig.1　Super-high pier analysis model

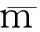
取橋墩中心線處的縱向位移為u(z,t),橫向位移v(z,t),則橋墩橫截面任意點處的縱向位移和橫向位移可表示為

u(x,z,t)=u(z,t)-xv′(z,t)

(1)

v(x,z,t)=v(z,t)

(2)

根據平截面假定,考慮超高橋墩大位移引起的幾何非線性影響,則橋墩中軸應變可表示為

(3)

式中:α為幾何非線性因子。當α=1時,為考慮幾何非線性;當α=0時,為不考慮幾何非線性。

利用經典桿件理論,結合桿件變形、內力的本構關系,橋墩軸力和彎矩可表示為

(4)

M(z,t)=-EIv″(z,t)

(5)

2動力控制方程

2.1超高橋墩動力微分方程

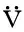
(6)

為建立結構的動力平衡方程,取橋墩z=r處截面以上部分進行內力、變形分析。圖2給出了超高橋墩動力分析的計算簡圖。

對圖2進行豎向軸力平衡分析,得到結構軸向力平衡方程

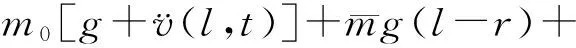
(7)

取隔離體對截面z=r處的彎矩平衡,得彎矩內力平衡方程

M(r,t)=0

(8)

將式(4)～式(6)代入式(7)、式(8)可得

(9)

(10)

式(9)和式(10)即為地震激勵下超高橋墩振動的動力控制微分方程。

圖2　橋墩動力分析簡圖Fig.2　Dynamic analysis diagram of pier

2.2邊界條件

(11)

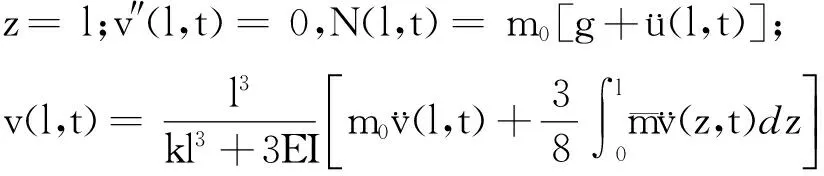
(12)

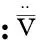
2.3初始條件

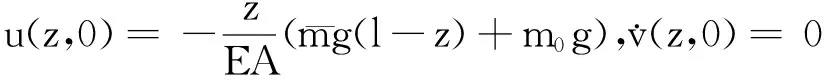
(13)

(14)

3求解方法

根據地震作用下超高橋墩振動的動力控制微分方程,結合橋墩模型的邊界條件和初始條件,假設其橫向和軸向位移形函數為

(15)

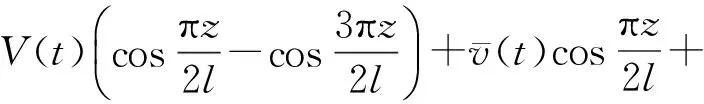
(16)

將式(15)和式(16)分別代入式(9)和式(10)中,化簡整理可得

(17)

(18)

式中各項系數為:

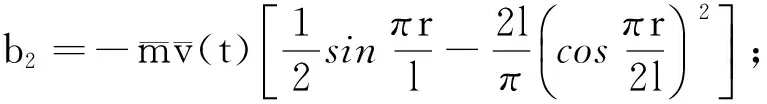
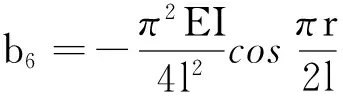
4數值算例

圖3　歸一化的部分El-Centro波Fig.3　Normalized partial El-Centro wave

為驗證本文理論正確性,在較小地震荷載作用下,按照本文方法編制Matlab計算程序計算得到橋墩頂端橫向位移時程,將其與利用有限元方法計算的結果進行對比。圖4給出了峰值加速度為10m/s2的地震荷載作用下橋墩頂橫向位移時程。由圖4可知,兩種方法計算結果差異較小、較為吻合,表明了本文理論的正確性。

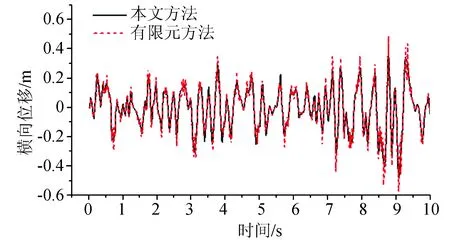
圖4　橋墩頂橫向位移曲線Fig.4　Lateral displacement curve on the pier top

圖5給出了各地震加速度荷載作用下結構的動力失穩時刻和加速度峰值。分析可知,在10m/s2峰值加速度荷載作用下,結構在10s內未因荷載的小幅變化而引起其位移參量的劇烈變化,即結構沒有出現動力失穩現象;而在加速度峰值荷載15m/s2作用下,結構在8.6s時出現動力失穩,失穩加速度荷載為amax=11.3m/s2;在20m/s2加速度峰值荷載作用時,結構動力失穩時刻為3.06s,對應的加速度荷載為amax=12.5m/s2;將地震波加速度荷載峰值增大至25m/s2時,結構的動力失穩時刻為0.68s,失穩加速度荷載amax=12.7m/s2。

圖5　墩頂位移時程曲線Fig.5　Displacement time history curve on the pier top

通過分析結構動力失穩時刻及其對應的結構失穩地震波加速度荷載值可得出以下結論:(1)該超高橋墩的動力失穩加速度在10m/s2

5結論

鑒于超高橋墩在強烈地震荷載作用下存在動力失穩的潛在危險,本文通過建立超高橋墩振動控制微分方程,利用變步長龍格-庫塔法對方程求解,結合B-R運動判定穩定準則,從數值解析角度對壓彎桿件進行了動力穩定性分析的理論研究。根據本文理論方法,通過編制Matlab計算程序,對算例中高柔橋墩在地震荷載作用下的動力穩定性進行了數值計算。結果表明,本文方法正確,超高橋墩的動力失穩時刻隨加速度荷載峰值的增大而減小,且兩者具有嚴格對應關系。算例分析結論表明,可根據本文方法準確預估結構失穩時刻和失穩加速度,這對超高橋墩的動力穩定研究和工程應用有重要意義。

參考文獻(References)

[1]HS阿爾喬姆,L艾登.梁-柱體系在橢圓型荷載作用下的精確解和動力屈曲分析[J].應用數學和力學,2010,31(10):1249-1255.HSecilArtem,LeventAydin.ExactSolutionandDynamicBucklingAnalysisofaBeam-columnSystemHavingtheEllipticTypeLoading[J].AppliedMathematicsandMechanics,2010,31(10):1249-1255.(inChinese)

[2]王安穩.軸向沖擊載荷下圓柱殼的塑性動力屈曲的問題[J].海軍工程大學學報,2004,16(6):1-8.

WANGAn-wen.PlasticDynamicBucklingofCylindricalShellsunderAxialImpulsiveLoads[J].JournalofNavalUniversityofEngineering,2004,16(6):1-8.(inChinese)

[3]韓強.彈塑性系統的動力屈曲和分叉[M].北京:科學出版社,2000.

HANQiang.DynamicBucklingandBifurcationofElastic-plasticSystems[M].Beijing:SciencePress,2000.(inChinese)

[4]孫強,楊大軍.彈性介質中桿的動力穩定性研究[J].工程力學,1997,14(1):87-91.

SUNQiang,YANGDa-jun.ResearchontheDynamicStabilityofPolesinElasticMedium[J].EngineeringMechanics,1997,14(1):87-91.(inChinese)

[5]孫強.伸出地而上基樁的動力穩定性研究[J].巖土工程學報,2003,25(4):459-462.

SUNQiang.AnalysisofDynamicStabilityofFoundationPileStretchingoutofGround[J].ChineseJounalofGeotechnicalEngineering,2003,25(4):459-462.(inChinese)

[6]徐艷,胡世德.地震作用下鋼管混凝土拱橋的動力穩定性[J].同濟大學學報:自然科學版,2007,35(3):315-320.

XUYan,HUShi-de.DynamicStabilityofConcreteFilledSteelTubularArchBridgeunderEarthquake[J].JournalofTongjiUniversity:NaturalScience,2007,35(3):315-320.(inChinese)

[7]BakkerMCM.Shear-flexuralBucklingofCantileverColumnsunderUniformlyDistributedLoad[J].JournalofEngineeringMechanics,2006,132(11):1160-1167.(inChinese)

[8]羅松南,李禮.沖擊荷載下高橋墩的彈塑性動力屈曲[J].振動與沖擊,2013,32(23):196-200.

LUOSong-nan,LILi.Elastic-plasticDynamicBucklingofaHighPierunderImpulseLoads[J].JournalofVibrationandShock,2013,32(23):196-200.(inChinese)

[9]羅松南,宋君晗,周慧.地基水平運動時高橋墩的動力屈曲[J].應用力學學報,2012,29(3):297-302.

LUOSong-nan,SONGJun-han,ZHOUHui.DynamicBucklingoftheHighPierundertheFoundationHorizontalMotionbyEarthquake[J].ChineseJournalofAppliedMechanics,2012,29(3):297-302.(inChinese)

[10]羅漪,王全鳳.變剛度薄壁桿件的動力穩定性[J].華僑大學學報:自然科學版,2001,22(3):272-277.

LUOYi,WANGQuan-feng.DynamicstabilityofThin-walledMemberwithVariableRigidity[J].JournalofHuaqiaoUniversity:NaturalScience,2001,22(3):272-277.(inChinese)

[11]盧皓,李建中.強震作用下高墩橋梁抗震性能特點分析[J].地震工程學報,2013,35(4):858-865.

LUHao,LIJian-zhong.AnalysisofSeismicPerformanceCharacteristicsofBridgewithHighPiersunderStrongEarthquakeMotion[J].ChinaEarthquakeEngineeringJournal,2013,35(4):858-865.(inChinese)

[12]夏修身,陳興沖,王常峰,等.高墩大跨連續剛構橋抗震性能研究[J].西北地震學報,2010,32(1):88-91.

XIAXiu-shen,CHENXing-chong,WANGChang-feng,etal.StudyonSeismicPerformanceofTall-pierandLong-spanContinuousRigid-framedBridge[J].NorthwesternSeismologicalJournal,2010,32(1):88-91.(inChinese)

[13]李黎,劉文靜,張行.地震作用下隔震橋梁的動力穩定分析[J].工程力學,2010,12(增刊Ⅱ):289-293.

LILi,LIUWen-jing,ZHANGHang.AnalysisonDynamicStabilityOfisolatedBridgesSubjectedtoEarthquake[J].EngineeringMechanics,2010,12(SupplⅡ):289-293.(inChinese)

[14]李黎,廖萍,龍曉鴻,等.薄壁高墩大跨度連續剛構橋的非線性穩定分析[J].工程力學,2006,23(5):119-124,88.

LILi,LIAOPing,LONGXiao-hong,etal.NonlinearStabilityAnalysisofLong-spanContinuousRigidFrameBridgewithThin-wallHighPiers[J].EngineeringMechanics,2006,23(5):119-124,88.(inChinese)

[15]孫華東.圓管和充液圓柱殼軸向沖擊動力屈曲[D].太原:太原理工大學,2000.

SUNHua-dong.DynamicBacklingofCircularTabeandFluid-filledCylindricalShellunderAxialImpact[D].Taiyuan:TaiyuanUniversityofTechnology,2000.(inChinese)

TheoreticalStudyontheDynamicStabilityofSuper-highBridgePiersunderStrongEarthquakes

CHENGMai-li1,2,LIQing-ning2,MIAORu-song2

(1.School of Architecture and Civil Engineering,Yan'an University,Yan'an 716000,Shaanxi,China;2.School of Civil Engineering,Xi'an University of Architecture and Technology,Xi'an 710055,Shaanxi,China)

Abstract：With the steady progress of transportation infrastructure construction in China,a large number of bridges with high piers have been built in the mountainous southwest region,a part of the Alpine-Himalayan seismic belt where earthquakes are frequent.Thus,research on structural seismic response has always attracted close attention.In this paper,we study the dynamic instability mechanism,seismic response,and performance of super-high bridge piers,develop reasonable structural strategies,and suggest design proposals to avoid dynamic instability.Assuming a plane section and considering the geometric non-linear effect induced by large displacement deformation of super-high piers,a numerical model of super-high piers is established.The governing differential equations of super-high piers are established,and a displacement shape function is proposed according to the force-deformation constitutive law of members.The Runge-Kutta method is used to solve the equation.Based on the B-R kinematic criterion,the dynamic instability mechanisms of super-high piers are discussed.The results from the numerical model under the dynamic conditions of various seismic waves are discussed,and longitudinal and lateral displacement at the top of high piers is studied.Theoretical analysis and calculation results show that the dynamic instability of super-high piers is closely related to pier geometry,mass distribution,and boundary conditions.The dynamic instability time of piers decreases with an increase in the peak acceleration of seismic waves.The relationship between the acceleration load and instability time shows strict correlation.The results from the example show that the method in this paper is simple,feasible,and correct.Using the theory in this paper,the dynamic instability time and acceleration load critical value of super-high piers can be calculated accurately.The theory is therefore significant in theoretical analysis and engineering practice regarding the dynamic instability of super-high piers.

Key words：strong earthquake; super-high bridge pier; dynamic stability; displacement shape function; Runge-Kutta method

收稿日期：①2015-10-15

基金項目：國家自然科學基金項目(51078306);國家青年基金項目(51408453);高等學校博士學科點專項科研基金(20106120110004);陜西省自然科學基礎研究計劃資助項目(2013JQ7007)

作者簡介：程麥理(1987-),男,博士,主要從事橋梁結構抗震分析研究。E-mail:cml3635@163.com。

中圖分類號:TU997

文獻標志碼：A

文章編號:1000-0844(2016)03-0360-06

DOI:10.3969/j.issn.1000-0844.2016.03.0360

程麥理1,2, 李青寧2, 苗如松2