混合邊界條件下廣義二維多項(xiàng)時(shí)間分?jǐn)?shù)階擴(kuò)散方程的解析解

王 學(xué) 彬

(武夷學(xué)院 數(shù)學(xué)與計(jì)算機(jī)學(xué)院，福建 武夷山 354300)

?

混合邊界條件下廣義二維多項(xiàng)時(shí)間分?jǐn)?shù)階擴(kuò)散方程的解析解

王 學(xué) 彬

(武夷學(xué)院 數(shù)學(xué)與計(jì)算機(jī)學(xué)院，福建 武夷山 354300)

廣義多項(xiàng)時(shí)間分?jǐn)?shù)階擴(kuò)散方程已被用于描述一些重要的物理現(xiàn)象，目前，有關(guān)該類方程在高維情形下滿足混合邊界條件的研究仍較少.利用分離變量法考慮有界區(qū)域上廣義二維多項(xiàng)時(shí)間分?jǐn)?shù)階擴(kuò)散方程，方程中關(guān)于時(shí)間變量的分?jǐn)?shù)階導(dǎo)數(shù)采用Caputo分?jǐn)?shù)階導(dǎo)數(shù)的定義，其階分別定義在[0,1],[1,2].而關(guān)于空間變量的偏導(dǎo)數(shù)則定義為傳統(tǒng)的整數(shù)階導(dǎo)數(shù)(二階)，得到了有界區(qū)域上廣義二維多項(xiàng)時(shí)間分?jǐn)?shù)階擴(kuò)散方程滿足非齊次混合邊界條件的解析解.亦可用于求解其他類型的滿足不同邊界條件的分?jǐn)?shù)階微分方程的解析解.

混合邊界條件；分離變量法；分?jǐn)?shù)階擴(kuò)散方程

分?jǐn)?shù)階微積分是一個(gè)古老又新鮮的概念，早在1695年HOSPITAL曾寫信給LEIBNIZ探討分?jǐn)?shù)階導(dǎo)數(shù)的意義[1].隨后，科學(xué)家們都致力于此領(lǐng)域的研究，但由于缺乏應(yīng)用背景的支撐，發(fā)展較為緩慢.近幾十年，許多領(lǐng)域的應(yīng)用研究發(fā)現(xiàn)，分?jǐn)?shù)階模型具有經(jīng)典的整數(shù)階模型無法比擬的優(yōu)勢和不可替代性，進(jìn)而分?jǐn)?shù)階微積分理論和應(yīng)用研究成為熱點(diǎn)[1-3].

近年來，涉及物理和力學(xué)過程的記憶和遺傳、路徑依賴和全局相關(guān)性的“反常” 擴(kuò)散引起了廣泛的關(guān)注[3].CHEN等[4]考慮了一維的多項(xiàng)時(shí)間分?jǐn)?shù)階電報(bào)方程，王學(xué)彬等[5-8]分別利用分離變量法、譜表示法等得到了幾類高維的時(shí)間、空間分?jǐn)?shù)階擴(kuò)散波動(dòng)方程的解，并考慮了高維的多項(xiàng)時(shí)間空間Caputo-Riesz分?jǐn)?shù)階擴(kuò)散方程的解析解[9].以上研究考慮的都是分?jǐn)?shù)階微分方程滿足第一類邊界條件即Dirichlet邊界條件下的定解問題.文獻(xiàn)[10]得到了一維的時(shí)間分?jǐn)?shù)階擴(kuò)散方程分別滿足第1類和第2類邊界條件下的解.本文將利用分離變量法得到廣義的二維多項(xiàng)時(shí)間分?jǐn)?shù)階方程滿足一定初始條件和非齊次混合邊界條件時(shí)的解析解.

1 預(yù)備知識(shí)

方便起見，先介紹文中用到的一些定義及引理.

定義1[1]α階Caputo分?jǐn)?shù)階導(dǎo)數(shù)定義如下：

m∈N.

(1)

定義2[11]對(duì)于實(shí)值函數(shù)(復(fù)值函數(shù))f(x),x>0,如果存在實(shí)數(shù)p>α使得f(x)=xpf1(x)，其中f1(x)∈C[0,∞].則稱f(x)∈Cα,α∈R.

定義4[12]多元Mittag-Leffler函數(shù)(n維情況)定義如下：

E(a1,…,an),b(z1,z2,…,zn)=

(2)

其中b>0,ai>0,|zi|<∞,i=1,2,…,n.

特別地，當(dāng)n=1時(shí)為常見的一元Mittage-Leffler函數(shù)：

(3)

引理1[12]當(dāng)μ>μ1>…>μn≥0,mi-1<μi≤mi,mi∈N0=N∪{0},λi∈R,i=1,2,…n.初值問題

(4)

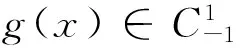
(5)

其中,

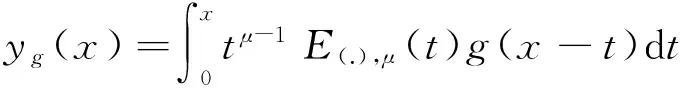
(6)

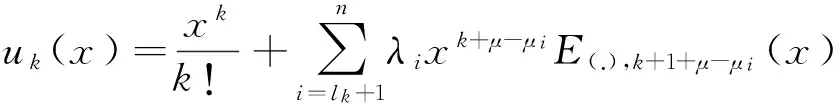
k=0,1,…,m-1.

(7)

E(.),β(x)=Eμ-μ1,…,μ-μn,β(λ1xμ-μ1,…,λnxμ-μn).

(8)

自然數(shù)lk,k=0,1,…,m-1, 且lk,k滿足條件mlk≥k+1,mlk+1≤k.當(dāng)mi≤k,i=1,2,…,n,取lk:=0,當(dāng)mi≥k+1,i=1,2,…n,取lk:=n.

2 廣義的二維多項(xiàng)時(shí)間分?jǐn)?shù)階擴(kuò)散方程滿足非齊次混合邊界條件的解析解

考慮如下二維廣義多項(xiàng)時(shí)間分?jǐn)?shù)階擴(kuò)散方程：

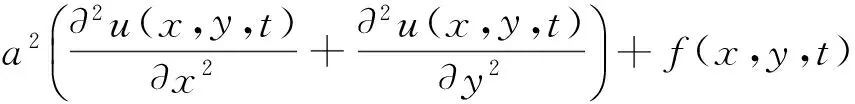
(9)

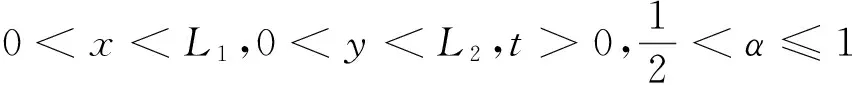
方程(9)滿足初始條件：

(10)

和非齊次混合邊界條件：

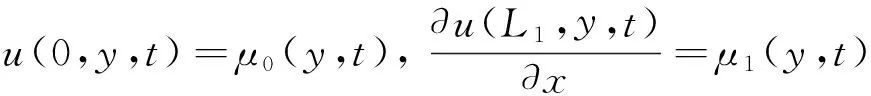
(11)

假設(shè)方程的解

u(x,y,t)=w(x,y,t)+v(x,y,t)，

(12)

其中v(x,y,t)=A(t)x2y2+B(t)xy+C(t)x+D(t)y滿足邊界條件(11).將v(x,y,t)代入式(11)有

(13)

解方程組(13)得

(14)

從而有

v(x,y,t)=x2y2[μ1(y,t)x-μ2(x,t)-

yμ3(x,t)+μ0(y,t)]/(2L1xy2-

2L2x2y)+μ2(x,t)+μ0(y,t)+

xy[2L1y2μ3(x,t)-2L1yμ0(y,t)-

2L2x2μ1(y,t)+2L2xμ2(x,t)]/

(2L1xy2-2L2x2y).

(15)

而函數(shù)w(x,y,t)滿足齊次邊值條件

(16)

其中，

(17)

首先假設(shè)w(x,y,t)=X(x)Y(y)T(t)，得到關(guān)于X(x),Y(y)的線性常微分方程：X″(x)+(λ-γ)X(x)=0， X(0)=X′(L1)=0，

(18)

Y″(y)+γY(y)=0， Y(0)=Y′(L2)=0，

(19)

及一個(gè)關(guān)于T(t)的分?jǐn)?shù)階線性常微分方程：

(20)

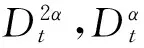
假設(shè)非齊次定解問題(16)的解有如下形式:

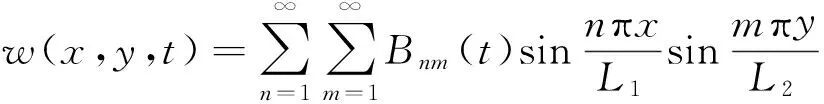
(21)

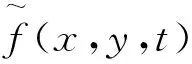
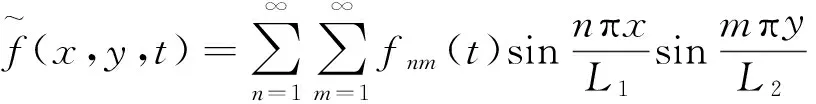
(22)

由式(22)可以得到

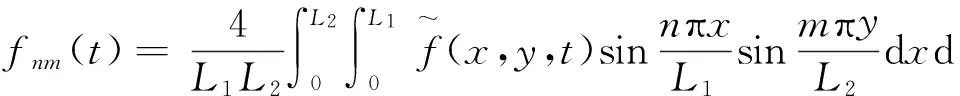
(23)

將式(21),(22)代入式(16)，有

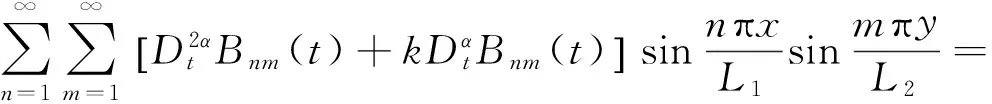
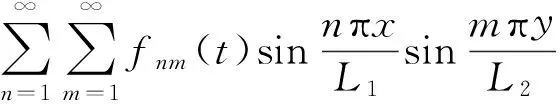
(24)

fnm(t).

(25)

因?yàn)閣(x,y,t)滿足式(16)中的初始條件，則有

(26)

進(jìn)一步可得

(27)

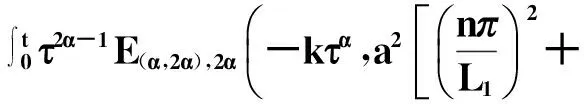
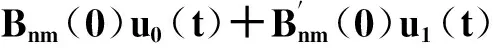
(28)

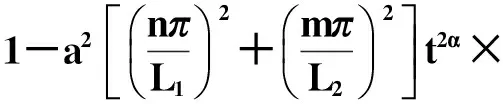
(29)

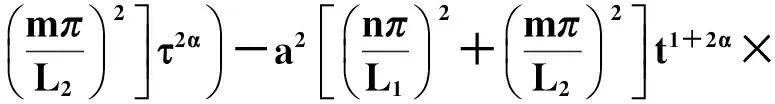
(30)

這里多元Mittag-leffler函數(shù)E(a1,a2,…,an),b(z1,z2,…,zn)如定義4所示.

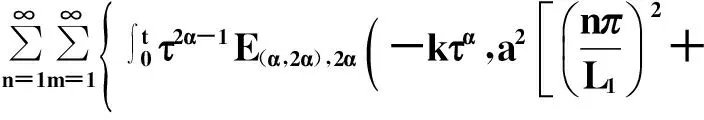
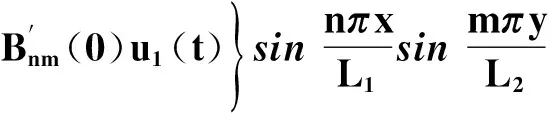
(31)

由式(12)、(15)、(31),得到二維廣義多項(xiàng)時(shí)間分?jǐn)?shù)階擴(kuò)散方程(9)滿足初始條件(10)和混合邊界條件(11)的解為

u(x,y,t)=w(x,y,t)+v(x,y,t)=

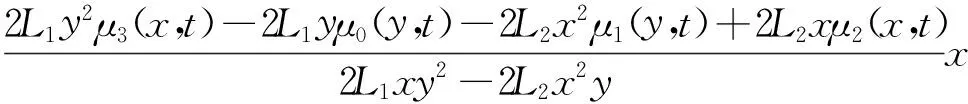
(32)

3 結(jié) 語

利用分離變量法考慮了二維廣義多項(xiàng)時(shí)間分?jǐn)?shù)階擴(kuò)散方程滿足非齊次混合邊界條件時(shí)的解析解問題.方程中將關(guān)于時(shí)間的分?jǐn)?shù)階導(dǎo)數(shù)定義為Caputo分?jǐn)?shù)階導(dǎo)數(shù)的形式、將關(guān)于空間變量的導(dǎo)數(shù)定義為經(jīng)典的整數(shù)階導(dǎo)數(shù),最后得到了由多元Mittag-Leffler函數(shù)表示的解,可將其推廣到三維廣義多項(xiàng)時(shí)間分?jǐn)?shù)階擴(kuò)散方程解析解的求解問題中.該方法可作為對(duì)整數(shù)階擴(kuò)散方程求解的推廣,也為求解滿足混合邊界條件的其他類型分?jǐn)?shù)階微分方程的定解問題提供了思路.

[1] PODLUBNY I. Fractional Differential Equations[M]. New York: Academic Press,1999.

[2] SAMKO S G，KILBAS A A，MARICHEV O I.Fractional Integrals and Derivatives：Theory and Applications[M].Amsterdam：Cordon and breach，1999.

[3] 陳文，孫洪廣，李西成.力學(xué)與工程問題的分?jǐn)?shù)階導(dǎo)數(shù)建模[M].北京：科學(xué)出版社，2010.

CHEN Wen, SUN Hongguang, LI Xicheng. Fractional Order Derivative Modeling of Mechanics and Engineering Problems[M]. Beijing: Science Press,2010.

[4] CHEN Jinhua, LIU Fawang, ANH V. Analytical solution for the time-fractional telegraph equation by the method of separating variables[J]. J Math Anal Appl,2008,338:1364-1377.

[5] 王學(xué)彬，劉發(fā)旺.分離變量法解三維的分?jǐn)?shù)階擴(kuò)散-波動(dòng)方程的初邊值問題[J].福州大學(xué)學(xué)報(bào):自然科學(xué)版，2007，35(4)：520-525.

WANG Xuebin, LIU Fawang. Separation of variables method for fractional diffusion-wave equation with initial-boundary value problem in three dimensions[J]. Journal of Fuzhou University: Natural Science Edition,2007，35(4)：520-525.

[6] 王學(xué)彬.一類二維空間Riesz分?jǐn)?shù)階擴(kuò)散方程的解[J].寧夏大學(xué)學(xué)報(bào):自然科學(xué)版，2011，32(3):222-225.

WANG Xuebin. Solutions of a kind of riesz fractional diffusion equation in two dimensions[J]. Journal of Ningxia University: Natural Science Edition,2011,32(3):222-225.

[7] 王學(xué)彬.二維、三維空間Riesz分?jǐn)?shù)階擴(kuò)散方程的基本解(英文)[J].山東大學(xué)學(xué)報(bào):理學(xué)版,2011,46(8):23-30.

WANG Xuebin. Fundamental solutions of fractional-in-space diffusion equation with Riesz fractional derivative in two and three dimensions[J].Journal of Shandong University:Natural Science,2011,46(8):23-30.

[8] 王學(xué)彬，劉發(fā)旺.二維和三維的時(shí)間分?jǐn)?shù)階電報(bào)方程的解析解[J].山東大學(xué)學(xué)報(bào):理學(xué)版，2012,47(8):114-121.

WANG Xuebin, LIU Fawang. Analytical solutions of the time-fractional telegraph equation in two and three dimensions[J]. Journal of Shandong University: Natural Science,2012,47(8):114-121.

[9] 王學(xué)彬.二維、三維的多項(xiàng)時(shí)間、空間Caputo-Riesz分?jǐn)?shù)階擴(kuò)散方程的解析解[J].山東大學(xué)學(xué)報(bào):理學(xué)版，2015,50(10)：89-94.

WANG Xuebin. Analytical solutions for the multi-term time-space Caputo-Riesz fractional diffusion equations in 2-D and 3-D[J]. Journal of Shandong University: Natural Science,2015,50(10)：89-94.

[10] JIANG Hui, LIU Fawang, TURNER I, et al. Analytical solutions for the multi-term time-space Caputo-Riesz fractional advetion-diffusion equations on a finite domain[J]. J Math Anal Appl,2012,389:1117-1127.

[11] DIMOVSKI I H. Convolution Calculus [M]. Sofia: Bulgarian Academy of Science,1982.

[12] LUCHKO Y. Initial-boundary-value problems for the generalized multi-term time-fractional diffusion equation[J]. J Math Anal Appl,2011,374:538-548.

Analytical solution of the generalized muti-term time-fractional diffusion equation in two-dimensions with mixed boundary condition.

WANG Xuebin

(SchoolofMathematicsandComputer，WuyiUniversity，Wuyishan354300，F(xiàn)ujianProvince，China)

Generalized multi-term time-fractional diffusion equations have been used to describe important physical phenomena. However, studies on multi-term time-fractional diffusion equations with mixed boundary conditions in high dimensional conditions are still limited. In this paper，a method of separating variables was effectively implemented to solve a generalized multi-term time-fractional diffusion equation (GMTDE) in a finite domain.In this equation, the multi-term time-fractional derivatives were defined in the Caputo sense, whose orders belonged to the intervals [0,1], [1,2], respectively. The space partial derivatives were classical integer order derivatives whose order were 2. We discussed and derived the analytical solution of the GMTDE in two dimensions meeting nonhomogeneous mixed boundary conditions.The technique reported can be applied to other kinds of fractional differential equations with different boundary conditions.

mixed boundary conditions；method of separating variables； time-fractional diffusion equation

2015-3-26.

福建省自然科學(xué)基金資助項(xiàng)目(2016J01682)；福建省本科高校教育教學(xué)改革研究項(xiàng)目(JAS151344)；武夷學(xué)院青年教師專項(xiàng)科研基金(xq201022)；武夷學(xué)院質(zhì)量工程項(xiàng)目(Jgzk201019).

王學(xué)彬(1976-)，ORCID:http://orcid.org/0000-0002-1066-3524，男，碩士，副教授，主要從事分?jǐn)?shù)階微積分研究，E-mail：wxbnp@163.com.

10.3785/j.issn.1008-9497.2016.04.005

O 241.82

A

1008-9497(2016)04-406-05

Journal of Zhejiang University(Science Edition), 2016,43(4):406-410