廣義中立型Emden-Fowler時滯阻尼微分方程的振動性

曾云輝, 李元旦, 羅李平, 羅振國

(衡陽師范學院 數學與統計學院， 湖南 衡陽 421008)

?

廣義中立型Emden-Fowler時滯阻尼微分方程的振動性

曾云輝, 李元旦*, 羅李平, 羅振國

(衡陽師范學院 數學與統計學院， 湖南 衡陽 421008)

研究了一類具有阻尼項的廣義中立型Emden-Fowler時滯微分方程的振動性.利用Riccati變換、積分平均技巧等方法，獲得了該方程解振動的充分條件，所得結果推廣和改進了最近研究中的一些結果.

中立型；Emden-Fowler方程；阻尼項；振動性

0 引 言

考慮廣義中立型Emden-Fowler時滯阻尼微分方程

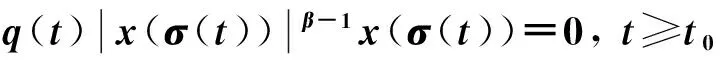
(1)

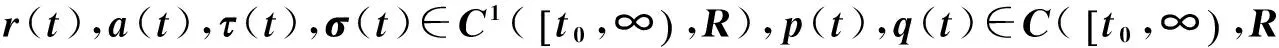
文中假設：

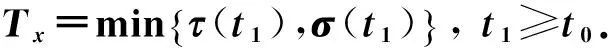
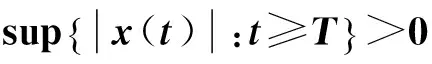
的解x(t).如果方程(1)的解有任意大的零點，稱為振動， 否則稱為非振動； 如果方程(1)的每一解均為振動，稱方程(1)為振動[1].

Emden-Fowler型方程在理論和實際應用上均有重要意義. 例如Emden-Fowler方程

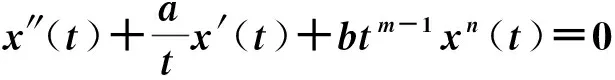
這里n≠0,n≠1,a,b,m是參數,在數學物理、理論物理及化學物理等領域有著廣泛應用[2].中立型Emden-Fowler方程在高速計算機無損線路的網絡設計中亦有廣泛應用[3]. 因此方程(1)的振動性問題引起了學者們的廣泛關注. 特別是如下特例：

(r(t)x′(t))′+q(t)x(t)=0，

(2)

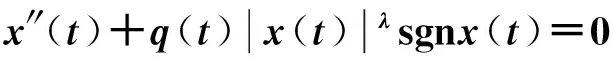
(3)

(r(t)[x(t)-p(t)x(t-c)]′)′+

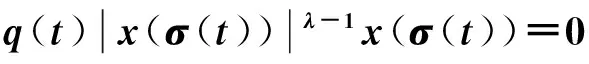
(4)

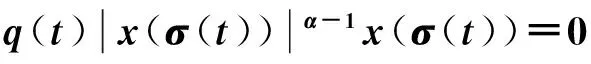
(5)

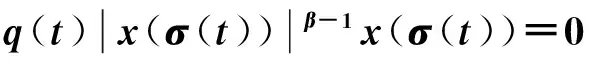
(6)

對于線性方程(2)的振動性,LEIGHTON[4]證明如下：

定理A設

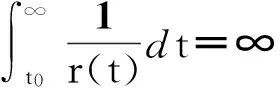
(7)

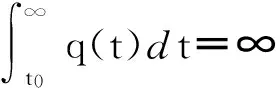
(8)

則方程(2)振動.

對于中立型方程(3),GRAMMATIKOPOULOS等[5]給出定理B.

定理B設0≤p(t)≤1,q(t)≥0,且

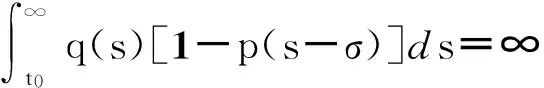
(9)

則方程(4)振動.

SUN等[6]對半線性方程(5)建立了如下振動準則：

定理C 設

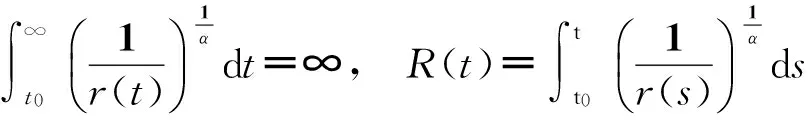
(10)

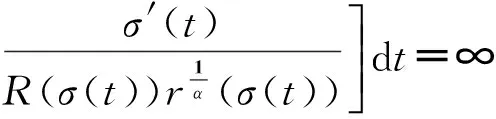
(11)

則方程(5)振動.

文獻[7]對中立型Emden-Fowler方程(6)建立了如下振動準則：

定理D設

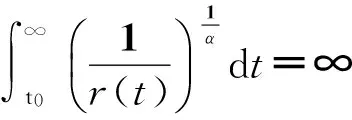
(12)

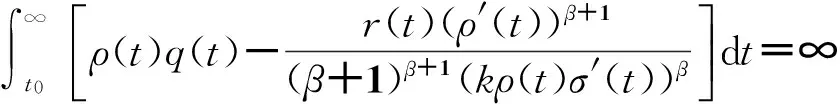
則方程(6)振動.

最近文獻[7]利用Riccati方法和積分平均技巧，得到了方程(6)當α≥β>0時的若干振動準則,推廣和改進了文獻中的一系列結果,受文獻[7]研究的啟發, 本文研究了方程(1)的振動性問題. 在α≥β條件下給出了方程(1)的振動條件,同時證明了當β≥α時方程(1)的新的振動定理,所得結果推廣并改進了若干文獻中的結果.

1 α≥β時的振動準則

定理1 設

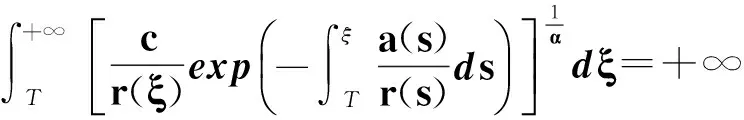
(13)

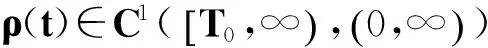
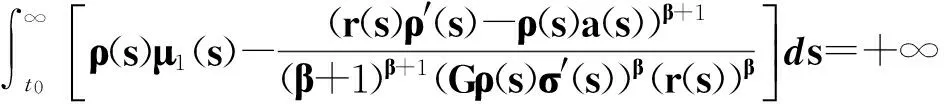
(14)

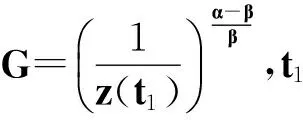
證明 設方程(1)有非振動解x(t),不失一般性，設x(t)>0,x(τ(t))>0,x(σ(t))>0,t≥t1≥t0(x(t)<0的情況可以類似證明),有

z(t)≥x(t)>0

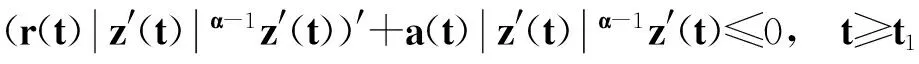
(15)

可斷言：

z′(t)≥0,t≥t1,且最終不恒為0.

(16)

不然, 則存在T≥t1≥t0, 當t=T時,z′(T)<0, 那么根據式(1),當t>T時,有

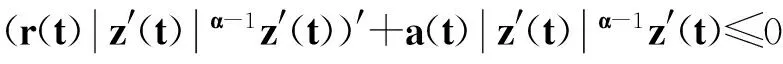
也就是

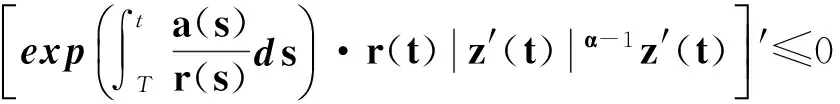
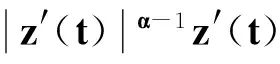
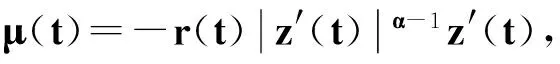
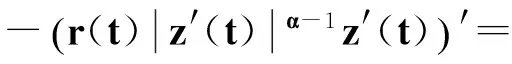
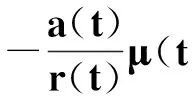
從而有

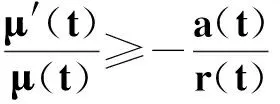
(17)

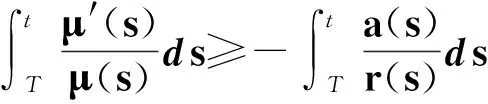
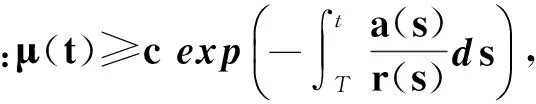
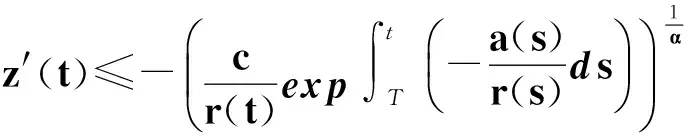
(18)

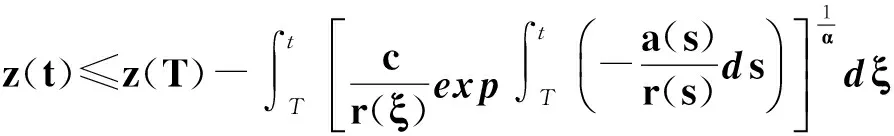
令t→∞，并結合式(14)有

,

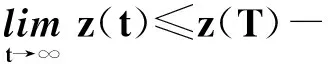
與z(t)>0矛盾. 故z′(t)≥0,且最終不恒為0. 因此有z″(t)≤0.

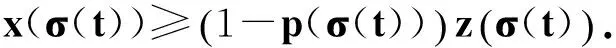
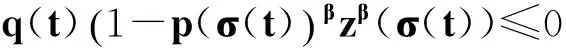
于是上式可寫為

μ1(t)zβ(σ(t))≤0.

(19)

定義函數

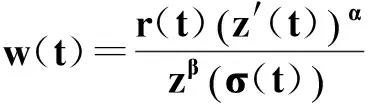
(20)

則w(t)>0.

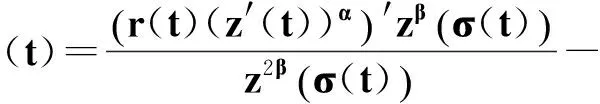
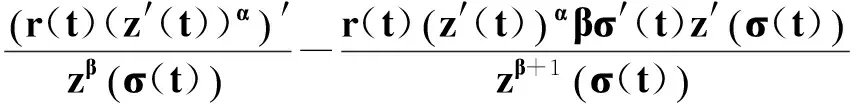
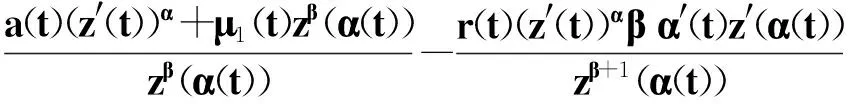
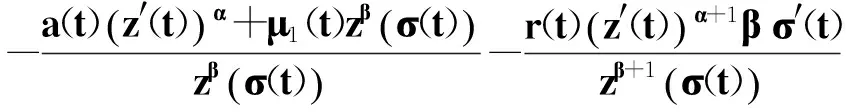
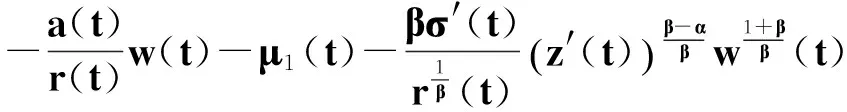
(21)

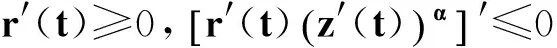
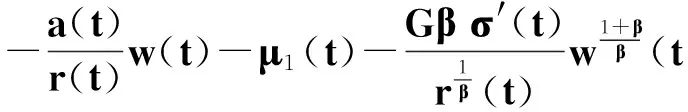
(22)

式(22)乘以ρ(t)并積分, 利用分部積分得到

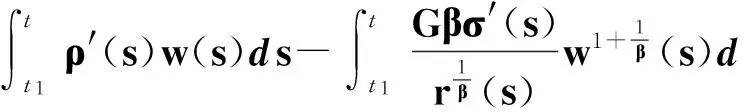
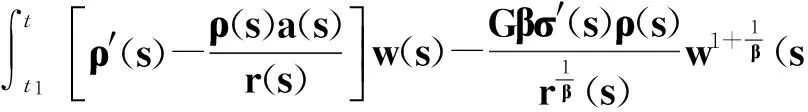
(23)

式(23)右端積分中利用不等式

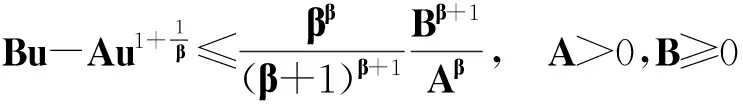
(24)

有

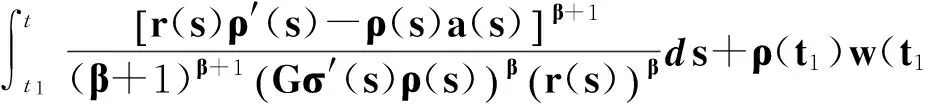
即

ρ(t1)w(t1).

(25)

得到式(25)與式(14)矛盾，定理1證畢.

推論1 如果定理1中ρ(t)=1,a(t)=0，且式(13)和(14)分別替換為

(26)

和

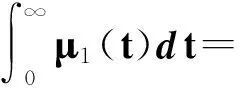
(27)

則方程(1)振動.

推論2 設ρ(t)=1,a(t)=0,r(t)=1且式(27)

成立, 則方程(1)振動.

注1 推論1推廣了定理A,推論2推廣了定理B. 因此 , 定理1推廣、改進并統一了著名的Leighton定理和Grammatikopounlms定理, 值得注意的是，推論1、2對任意α>0,β>0都成立.

例1 考慮中立型微分方程

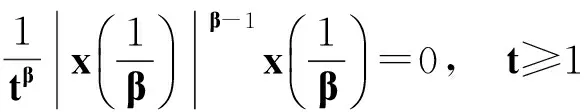
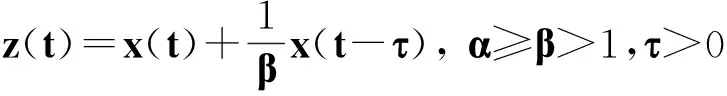
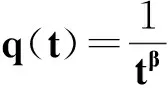
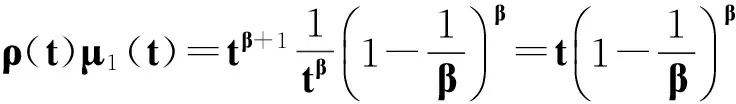
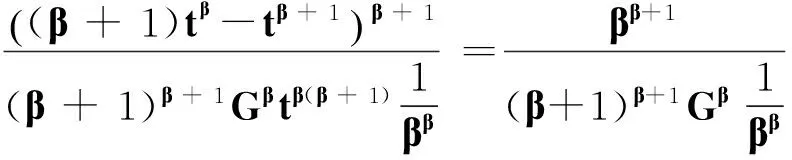
因此，

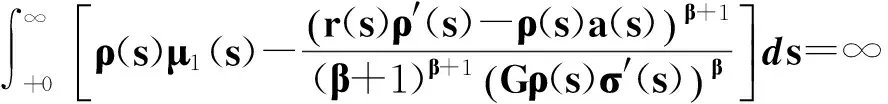
現令

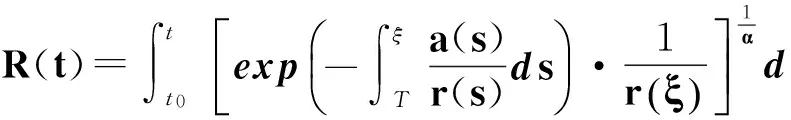
定理2 設式(13)成立,式(27)不成立，若

α>β>0，且

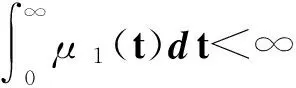
(28)

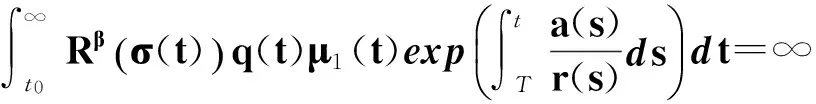
(29)

則方程(1)振動.

證明 設方程(1)存在非振動解x(t)，不失一般性,設x(t)最終為正,則z(t)≥x(t)>0,t≥t1,如同定理1的證明，有式(17)和(7)成立. 即

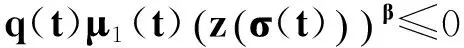
也就是

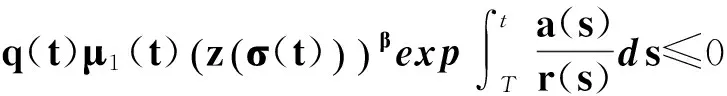
對上式積分，有

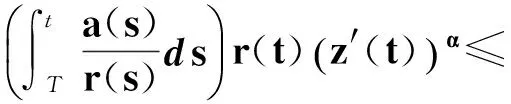
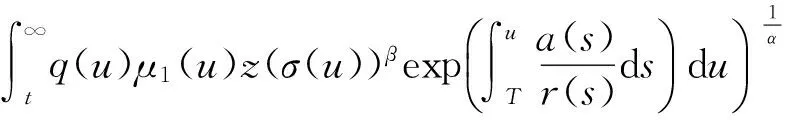
(30)

對式(30)積分，有

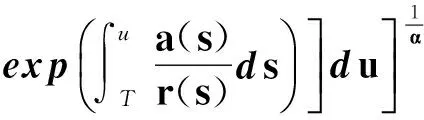
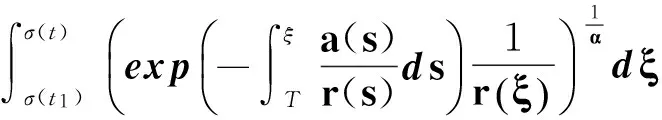
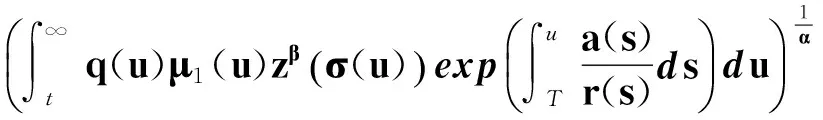
即

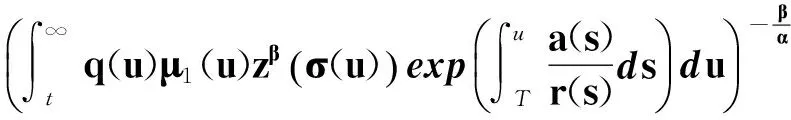
(31)

定義函數

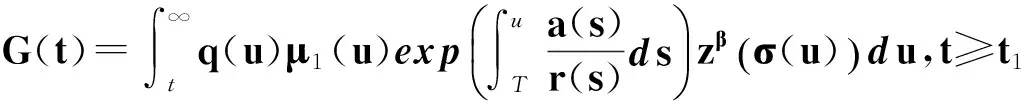
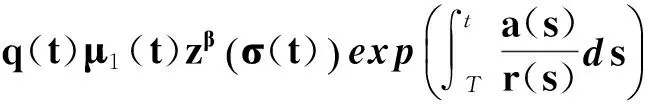
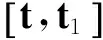
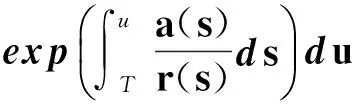
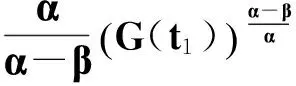
(32)

注意到式(28)成立,故式(32)與式(29)矛盾.定理2證畢.

注2 文獻[8]的定理3.1是本文定理2當p(t)=0,a(t)=0時的特例.將結果推廣到了中立型阻尼方程.

下面的定理對任意α>0,β>0均成立，如果滿足：

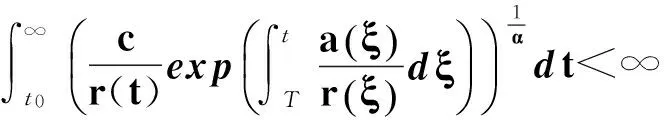
(33)

方程(1)稱為是非正則的，現在考慮在非正則條件下，方程(1)的振動性.

定理3 設式(33)和(27)成立，若p′(t)≥0,τ′(t)>0,x′(t)x′(τ(t))>0,且

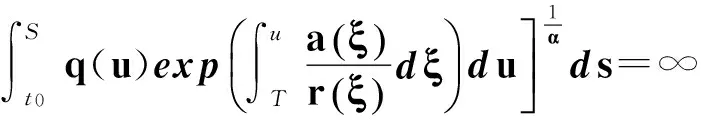
(34)

證明 設方程(1)有最終正解x(t)(對于有最終負解x(t)的情況可以類似證明),如同定理1的證明，知z′(t)最終定號. 故z′(t)有2種情況：

情況(i)：若z′(t)>0,t≥t1≥t0.即式(16)成立，類似定理1的證明，結果與式(17)矛盾.

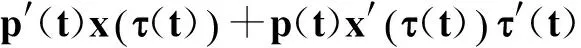
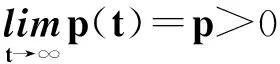
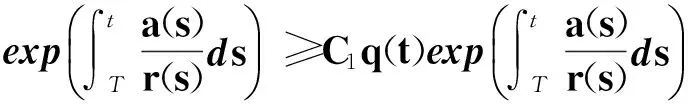
(35)

對式(35)積分,有

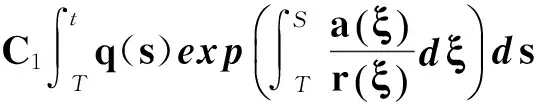
即

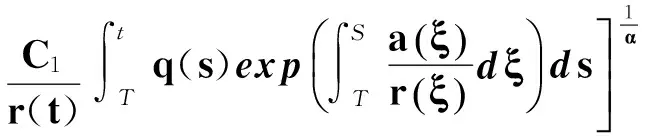
(36)

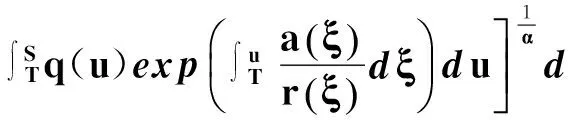
(37)

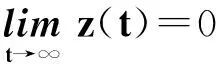
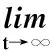
2 β≥α時的振動準則

注意到對方程(1)振動性的研究，大多考慮α≥β的情況，而本文給出了當β≥α時方程(1)的2個振動準則.

引理1 設式(13)成立，且

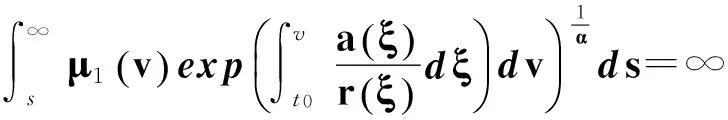
(38)

證明 設x(t)>0,t≥t1≥t0，由定理1的證明知式(16)和(19)成立. 即z′(t)>0且有

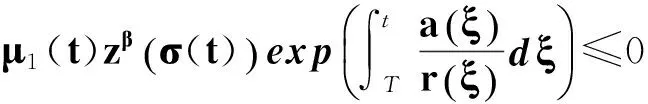
(19′)

若z(t)有界，則存在c1,c2>0，使得

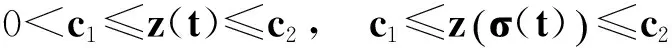
(39)

對式(19′)積分，有

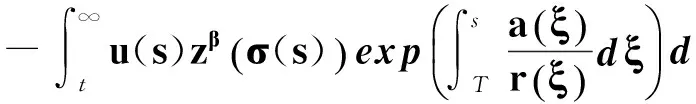
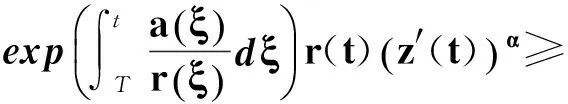
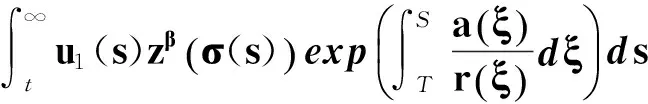
即

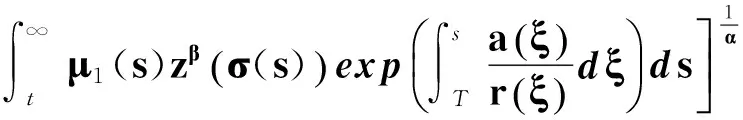
對上式在[t1,t]上積分，有

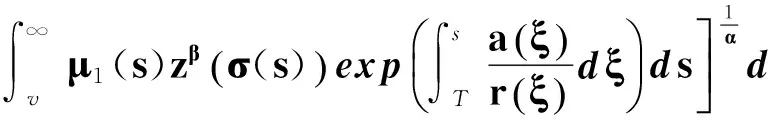
利用式(39)得到

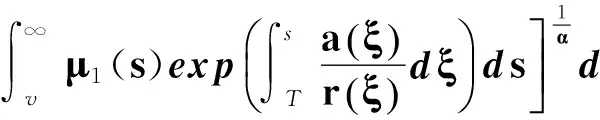
(40)

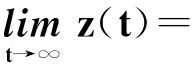
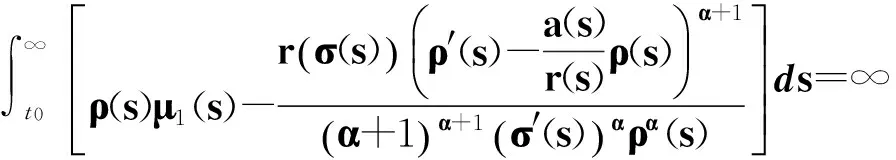
(41)

則方程(1)振動.

證明 設方程(1)有非振動解x(t). 不失一般性, 設x(t)是式(1)的最終正解. 如同定理1的證明，有式(16)和(19)成立. 定義函數同式(20), 即

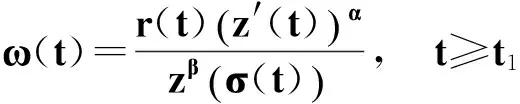
則

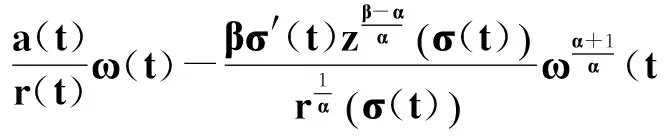
(42)

上式中利用了不等式

和式(19).下面在式(42)中利用引理1及β≥α， 得

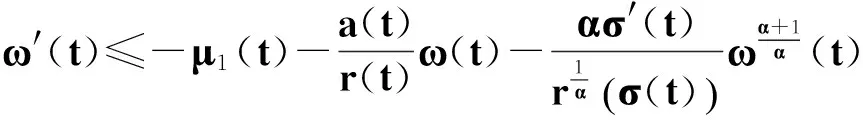
t≥T≥t1.

(43)

式(43)乘以ρ(t)，積分有

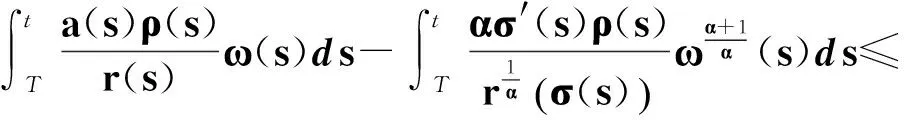
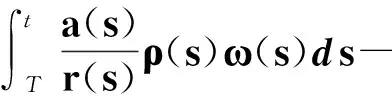
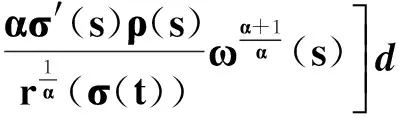
(44)

在式(44)右端積分中利用不等式:

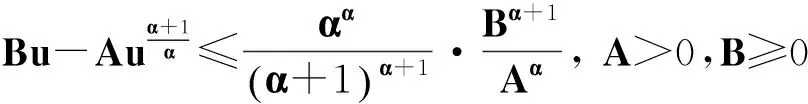
(45)

得

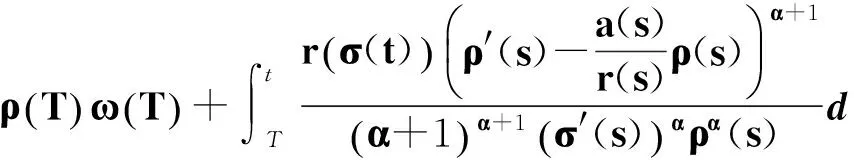
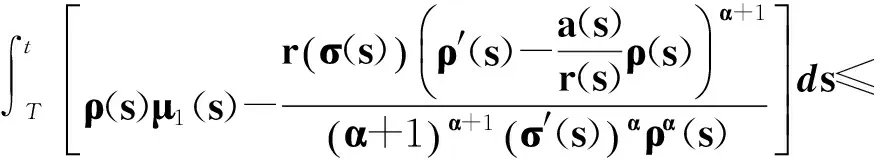
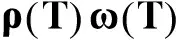
(46)

顯然式(46)與式(41)矛盾. 定理3證畢.

注4 定理4推廣并改進了文獻[6]和[8]的主要結果. 只須取α=β,p(t)=0,a(t)=0,ρ(t)=Rα(σ(t))即可. 同時定理4也統一了定理A～D.

推論3 設r(t)=1,α>1, 式(38)成立，若

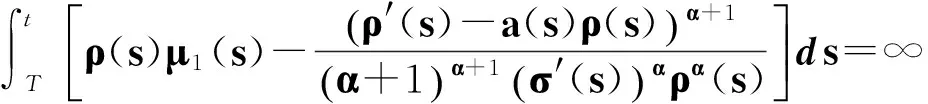
(47)

則方程(1)振動.

下面給出當式(27)不成立時，方程(1)的另一個振動準則.為簡化計算，設

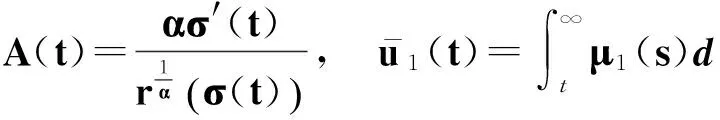
(48)

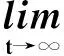
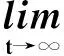
(49)

則方程(1)振動.

證明 設方程(1)有非振動解x(t)，定義函數ω(t),同定理4的證明，知式(43)成立，即

t≥T≥t1.

(50)

對式(50)積分，有

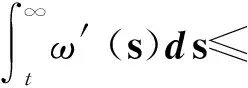
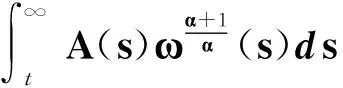
從而

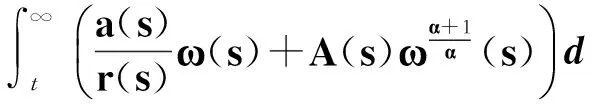
(51)

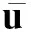
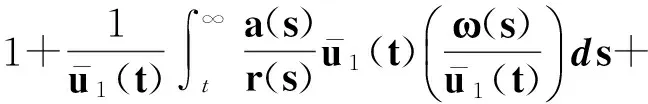
(52)

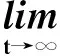
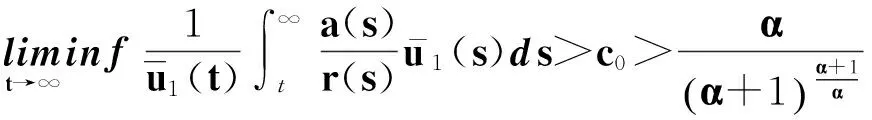
(53)

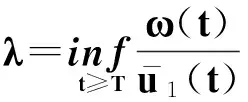
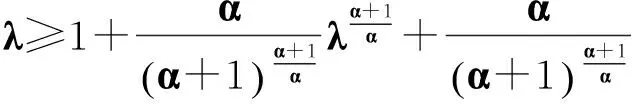
(54)

利用不等式(45),其中，

得到

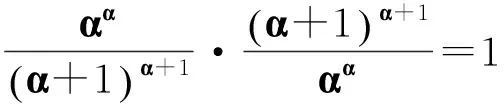
(55)

顯然式(55)與式(54)矛盾. 故方程(1)無非振動解，定理5證畢.

[1]LIUL,BAIY.Newoscillationcriteriaforsecondordernonlineardelayneutraldifferentialequations[J].JComputApplMath,2009,231:657-663.

[2] 李同興, 韓振來, 張承慧, 等. 時間尺度上三階Emden-Fowler時滯動力方程振動準則[J]. 數學物理學報,2012,32(1):222-232.

LITongxing,HANZhenlai,ZHANGChenghui,etal.Oscillationcriteriaforthird-orderemden-fowlerdelaydynamicequationsontimescales[J].ActaMathematicaScientia,2012,32(1):222-232.

[3]LIT,HANZ,ZHANGC,etal.OntheoscillationofsecondorderEmden-Fowlerneutraldifferentialequations[J].JApplMathComput,2011,37:601-610.

[4]LEIGHTONW.Thedetectionoftheoscillationsofsolutionsofasecondorderlineardifferentialequation[J].DukeMathJ,1950,17:57-62.

[5]GRAMMATIKOPOULOSMK，LADASG，MEIMARIDOUA.Oscillationsofsecondorderneutraldelaydifferentialequations[J].RadMath,1985(1):267-274.

[6]SUNYG，MENGFW.NoteonthepaperofDzurinaandStavroulakis[J].ApplMathComput,2006,174:1634-1641.

[7]LIUHD,MENGFW,LIUPH.OscillationandasymptoticanalysisonanewgeneralizedEmden-Fowlerequation[J].ApplMathComput,2012,219:2739-2748.

[8]BACULIKOVAB,LIT,DZURINAJ.Oscillationtheoremsforsecondordersuperlinearneutraldifferentialequations[J].MathematicsSlovaca,2013,63:123-134.

Oscillation of generalized neutral delay differential equations of Emden-Fowler type with damping.

ZENG Yunhui, LI Yuandan, LUO Liping, LUO Zhenguo

(CollegeofMathematicsandStatistics,HengyangNormalUniversity,Hengyang421008,HunanProvince,China)

Oscillation of generalized neutral delay differential equations of Emden-Fowler type with damping was studied. By using of Riccati transformation and integral inequality technique, we obtained some new sufficient conditions for oscillation of all solutions of the equation, which generalized and improved some known results.

neutral type; Emden-Fowler differential equation; damping term; oscillation

2015-06-10.

湖南省“十二五”重點建設學科“運算學與控制論”項目資助(湘教發[2011]76號)；湖南省科技廳軟科學研究計劃項目資助(2014ZK3009);衡陽市科技計劃項目資助(2014KJ22);衡陽市社科基金項目資助(2014DD60);湖南省教育廳科研項目資助(14C0170).

曾云輝(1978-)，ORCID:http://orcid.org/0000-0003-2620-2738,男，碩士，副教授，主要從事微分方程定性理論研究,E-mail:chj8121912@sina.com.

*通信作者，ORCID:http://orcid.org/0000-0002-6729-1688,E-mail:18973416616@189.cn.

10.3785/j.issn.1008-9497.2016.04.003

O 175.26

A

1008-9497(2016)04-394-07

Journal of Zhejiang University (Science Edition),2016,43(4):394-400