線形、梳形和星形高分子靜態和動態性質的模擬

潘　凱, 朱有亮, 付翠柳, 黃以能, 孫昭艷

(1. 伊犁師范學院物理科學與技術學院, 新疆凝聚態相變與微結構實驗室, 伊寧 835000;2. 中國科學院長春應用化學研究所, 高分子物理與化學國家重點實驗室, 長春 130022;3. 南京大學物理學院, 固體微結構物理國家重點實驗室, 南京 210093)

?

線形、梳形和星形高分子靜態和動態性質的模擬

潘凱1,2, 朱有亮2, 付翠柳2, 黃以能1,3, 孫昭艷1,2

(1. 伊犁師范學院物理科學與技術學院, 新疆凝聚態相變與微結構實驗室, 伊寧 835000;2. 中國科學院長春應用化學研究所, 高分子物理與化學國家重點實驗室, 長春 130022;3. 南京大學物理學院, 固體微結構物理國家重點實驗室, 南京 210093)

摘要以梳形高分子為紐帶, 基于粗粒化分子動力學模擬方法, 研究了線形、 梳形和星形拓撲結構高分子的靜態和動態性質, 以揭示稀溶液中高分子鏈行為與鏈拓撲結構依賴關系的一般性規律. 研究結果表明, 隨著線形-梳形-星形的鏈拓撲結構轉變, 回轉半徑的標度關系由僅依賴分子聚合度轉變為同時依賴鏈聚合度與臂數或側鏈數. 分析了星形高分子和梳形高分子的靜態和動態性質的特征規律. 星形高分子的臂數增加使其尺寸迅速減小, 形狀則由長橢球形轉變為類球形, 且擴散系數也隨之增加; 其均方回轉半徑(〈Rg〉)和擴散系數(D)與分子聚合度(N)及臂數(f)的標度規律為〈Rg〉～N0.581f-0.402,D～N-0.763f0.227. 梳形高分子的靜態與動態性質與分子聚合度及側鏈數的依賴關系為〈Rg〉～N0.597f-0.212(每個支化點只有一條側鏈)和〈Rg〉～N0.599f-0.316(每個支化點有多條側鏈).

關鍵詞分子動力學模擬; 星形高分子; 梳形高分子; 均方回轉半徑; 擴散系數

1956年, Szwarc等[1]利用活性陰離子聚合方法制得嵌段共聚物. 隨著原子轉移自由基聚合(ATRP)等合成技術的發現, 人們已經能合成出, 線形、 環形、 星形、 梳形及樹枝形等復雜鏈拓撲結構的高分子, 使得研究不同鏈拓撲結構高分子的靜態和動態性質成為可能[2～12]. 眾所周知, 結構決定性能, 高分子溶液的熱力學及流變學性質均與其構象等微觀特性相關, 因此, 從微觀角度出發, 在分子水平上研究多種鏈拓撲結構高分子的靜態和動態性質在理論研究和實際應用中都有重要意義.

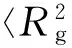
線形、 梳形和星形是3種比較典型的高分子鏈拓撲結構. 線形高分子相當于側鏈長度極短的梳形高分子, 星形高分子相當于主鏈長度極短的梳形高分子, 基于梳形高分子可以實現從線形到星形高分子的過渡. 因此, 本文以梳形高分子為紐帶, 研究了稀溶液中線形-梳形-星形的鏈拓撲結構轉變對高分子靜態和動態性質的影響, 得到其標度行為規律, 進而獲得高分子的靜態和動態性質與鏈拓撲結構(包括分子聚合度和臂數或側鏈數等因素)的依賴關系.

1模擬方法

基于粗粒化分子動力學(MD)方法, 研究了稀溶液中不同鏈聚合度、 臂數及側鏈數的線形、 梳形和星形高分子的靜態與動態性質(見圖1).

模型中所采用的高分子鏈為珠簧鏈, 相鄰高分子單體之間存在作用勢(UFENE):

(1)

式中:r為高分子鏈上相鄰的單體間的距離;k為彈簧常數;r0為極限長度. 在約化單位下, 取k=7.0ε/σ2,r0=2.0σ[以能量單位ε、 長度單位σ和溶劑質量m為基本單位, 時間單位則為τL-J=σ(m/ε)1/2]. 高分子單體與溶劑粒子具有相同的質量. 所有單體和溶劑粒子之間存在截斷Lennnard-Jones作用勢(UL-J):

(2)

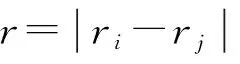
模擬所用積分步長為0.006τL-J, 體系的粒子數密度為ρ=0.864, 溫度為kBT=1.0. 松弛2×106時間步系統達到平衡后, 繼續運行1×107時間步(1時間步=0.006τL-J), 每10000時間步記錄一次體系的物理性質. 分子動力學模擬方法來源于GALAMOST GPU軟件包[27].

2結果與討論

2.1線形、 梳形和星形高分子的靜態和動態性質

為了直接對比線形、 梳形、 星形高分子不同靜態和動態行為, 首先研究了具有典型結構的3種高分子, 其中梳形高分子支化點數n=5, 每個支化點的側鏈數fn=1; 星形高分子為五臂星形高分子. 高分子鏈尺寸可以用回轉半徑來表征. 圖2給出線形、 梳形和五臂星形的回轉半徑和擴散系數與鏈聚合度的依賴關系. 由圖2可見, 不同拓撲結構高分子的分子尺寸差異顯著, 線形鏈尺寸最大, 而星形鏈尺寸最小; 而不同鏈結構高分子的擴散差異并不明顯, 隨著聚合度的增加, 擴散系數均迅速衰減.

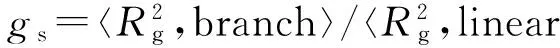
2.2星形高分子的靜態和動態性質及標度行為

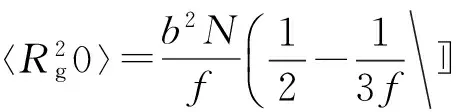
圖7給出不同鏈結構星形高分子的擴散系數與分子聚合度及臂數的依賴關系. 隨著臂數的增加, 星形高分子的擴散系數迅速增大[圖7(A)], 三臂星形擴散最慢, 而十五臂星形擴散最快. 隨著聚合度增加, 星形高分子的擴散系數迅速衰減, 并且不同臂數的星形高分子的擴散行為的差異有所減小, 與前期的模擬結果相似[23]. 擴散系數與分子聚合度及星形高分子臂數的標度關系(D～N-0.763f0.227)如圖7(B)所示, 這一結果比較接近Zimm模型[31～33]的預測, 即Dz=kBT/ηs〈Rg〉.

2.3梳形高分子的靜態標度行為

對于梳形高分子, 當主鏈較長且側鏈較短時, 其結構與動力學性質呈現接近線形鏈的特征行為; 而當主鏈較短側鏈較長時, 梳形高分子則呈類星形鏈行為. 因此, 本文以梳形高分子為紐帶, 能夠實現線形-梳形-星形的結構轉變, 有助于分析獲得高分子的靜態和動態性質與鏈拓撲結構的依賴規律. 保持梳形高分子的接枝密度σ=Ns/Nm=3.0, 研究了不同長度的主鏈Nb和側鏈Ns梳形高分子的分子尺寸和擴散性質, 其中Nm為兩側鏈間的主鏈的間隔長度[Nm=Nb/(n+1),n為支化點數]. 圖8給出支化點n=2, 3, 4, 5的5種梳形高分子的分子尺寸和擴散系數與分子聚合度的變化關系圖(每個節點連接的側鏈數為fn=1, 則梳形分子的總側鏈數為f=nfn). 由圖8可見, 支化點數目越多, 梳形高分子的分子尺寸越小, 其回轉半徑與分子聚合度及側鏈數相關〈Rg〉～N0.597f-0.212, 但擴散差距不明顯. 進一步增加每個支化點的fn, 可獲得不同支化點的星形高分子的回轉半徑與聚合度及側鏈數之間的標度關系〈Rg〉～Nνfα, 結果列于表1. 可以看出, 不同支化點(n=2,3,4,5)的梳形高分子的回轉半徑與分子聚合度的關系相近, 均方回轉半徑的標度關系為〈Rg〉～N0.599f-0.316. 以上結果說明, 每個節點上所連接側鏈的增多, 會導致梳形高分子的回轉半徑與側鏈數的依賴性顯著增強.

3結論

基于粗粒化分子動力學方法, 本文系統研究了線形、 梳形、 星形高分子的靜態和動態性質, 得到了不同拓撲結構高分子的均方回轉半徑及擴散系數的變化關系, 并進一步得到了梳形和星形高分子的靜態和動態性質與分子聚合度及臂數或側鏈數的標度關系. 研究發現, 星形高分子具有最小的分子尺寸, 線形高分子的尺寸最大, 但擴散系數差異并不明顯. 隨著鏈結構發生由線形到梳形再到星形的改變, 均方回轉半徑的標度關系由僅依賴分子聚合度轉變為同時依賴鏈聚合度和分子臂數或側鏈數. 本文的模擬結果可以幫助人們在分子水平上認識高分子靜態和動態行為的物理本質.

參考文獻

[1]Szwarc M., Levy M., Milkovich R.,J.Am.Chem.Soc., 1956, 78, 2656—2657

[2]Jeon C., Kim J., Jeong H., Jung Y., Ha B. Y.,SoftMatter, 2015, 11, 8179—8193

[3]Liu H. H., Tang D. D., Tang R. P., Zhao Y. L.,Sci.ChinaChem., 2015, 58(11), 1724—1733

[4]Jung Y., Jeon C., Kim J., Jeong H., Jun S., Ha B. Y.,SoftMatter, 2012, 8, 2095—2102

[5]Mikhaylov I. V., Darinskii A. A.,Polym.Sci.Ser.A, 2015, 57(2), 239—250

[6]Potemkin I. I., Palyulin V. V.,Polym.Sci.Ser.A, 2009, 51(2), 123—149

[7]Zhang L. L., Chen Q. Y., Zhou H. W., Shi T. F., Huang Y. N.,Chem.J.ChineseUniversities, 2015, 36(9), 1832—1837(張麗麗, 陳巧悅, 周恒為, 石彤非, 黃以能.高等學校化學學報, 2015, 36(9), 1832—1837)

[8]Jabbarzadeh A., Atkinson J., Tanner R.,Macromolecules, 2003, 36(13), 5020—5031

[9]Rouault Y., Borisov O. V.,Macromolecules, 1996, 29(7), 2605—2611

[10]Santangelo P. G., Roland C. M., Puskas J. E.,Macromolecules, 1999, 32(6), 1972—1977

[11]Deffieux A., Schappacher M.,Macromolecules, 1999, 32(6), 1797—1802

[12]Khabaz F., Khare R.,J.Chem.Phys., 2014, 141, 214904

[13]Aust C., Kroger M., Hess S.,Macromolecules, 1999, 32(17), 5660—5672

[14]Fu C. L., Sun Z. Y., An L. J.,ChineseJ.Polym.Sci., 2013, 31(3), 388—398

[15]Fetters L. J., Hadjichristidis N., Lindner J. S., Mays J. W.,J.Phys.Chem.Ref.Data, 1994, 23(4), 619—640

[16]Hsu H. P., Nadler W., Grassberger P.,Macromolecules, 2004, 37(12), 4658—4663

[17]Hou J. X., Huang Z. W., Li M. Z., Chen Y., Xiao Q. T., Zhang Y. H., Yang J.,Chem.J.ChineseUniversities, 2015, 36(12), 2610—2614 (侯吉旋, 黃子文, 李明澤, 陳瑤, 肖屹彤, 章燁暉, 楊景. 高等學校化學學報, 2015, 36(12), 2610—2614)

[18]Grest G. S., Kremer K., Witten T. A.,Macromolecules, 1987, 20(6), 1376—1383

[19]Chen W. D., Chen J. Z., An L. J.,SoftMatter, 2013, 9, 4312—4318

[20]De Gennes P. G.,ScalingConceptsinPolymerPhysics, Cornell University Press, Ithaca, 1979, 25—46

[21]Rubinstein M., Colby R. H.,PolymerPhysics, Oxford University Press, New York, 2003, 102—104

[22]Jagodzinski O., Eisenriegler E., Kremer K.,J.Phys.I, 1992, 2(12), 2243—2279

[23]Fu C. L., Ouyang W. Z., Sun Z. Y., An L. J.,J.Chem.Phys., 2007, 127, 044903

[24]Brown S., Szamel G.,Macromol.Theor.Simul., 2000, 9(1), 14—19

[25]Sikorski A.,Macromol.Chem.Theor., 1993, 2(3), 309—318

[26]Fu C. L., Sun Z. Y., An L. J.,J.Phys.Chem.B, 2011, 115(39), 11345—11351

[27]Zhu Y. L., Liu H., Li Z. W., Qian H. J., Milano G., Lu Z. Y.,J.Comput.Chem. 2013, 34(25), 2197—2211

[28]Zimm B. H., Stockmayer W. H.,J.Chem.Phys., 1949, 17(12), 1301—1314

[29]Timoshenko E. G., Kuznetsov Y. A., Connolly R.,J.Chem.Phys., 2002, 116(9), 3905—3916

[30]Connolly R., Timoshenko E. G., Kuznetsov Y. A.,J.Chem.Phys., 2003, 119(16), 8736—8746

[31]Zimm B. H.,J.Chem.Phys., 1956, 24(2), 269—278

[32]Dunweg B., Kremer K.,J.Chem.Phys., 1993, 99(2), 6983—6997

[33]Doi M., Edwards S. F.,TheTheoryofPolymerDynamics, Oxford University Press, New York, 1986, 97—104

(Ed.: W, Z)

? Supported by the National Basic Research Program of China(No.2012CB821500) and the National Natural Science Foundation of China(Nos.21222407, 21404102, 21474111, 21104082).

Simulation on the Static and Dynamic Properties of Linear, Comb-like and Star-like Polymers?

PAN Kai1,2, ZHU Youliang2, FU Cuiliu2*, HUANG Yineng1,3, SUN Zhaoyan1,2

(1.XinjiangLaboratoryofPhaseTransitionsandMicrostructuresinCondensedMatterPhysics,CollegeofPhysicalScienceandTechnology,YiliNormalUniversity,Yining835000,China;2.StateKeyLaboratoryofPolymerPhysicsandChemistry,ChangchunInstituteofAppliedChemistry,ChineseAcademyofSciences,Changchun130022,China;3.SchoolofPhysics,NationalLaboratoryofSolidStateMicrostructures,NanjingUniversity,Nanjing210093,China)

KeywordsMolecular dynamics simulation; Star-like polymer; Comb-like polymer; Radius of gyration; Diffusion coefficient

AbstractWe studied the static and dynamic properties of linear, comb-like and star-like polymers by means of molecular dynamics method. We found star-like polymers had the smallest size, and linear polymers had the largest size at the same chain length. Changing the chain topologies from linear to comb-like and star-like will lead to the great dependence of the scaling relationship of radius of gyration on both the degree of polymerization and the number of side chains or the arms. For star polymers, the increase of the number of arms results inthe decrease of the radius of gyration and increase of the diffusion coefficients. Moreover, the scaling relationship for radius of gyrations for star polymers and comb polymer is also obtained. These results may help people understand the physical insight of the topological structure dependence on the static and dynamic properties of polymer chains.

收稿日期:2016-01-24. 網絡出版日期: 2016-04-30.

基金項目:國家“九七三”計劃項目(批準號: 2012CB821500)和國家自然科學基金(批準號: 21222407, 21404102, 21474111, 21104082)資助.

中圖分類號O631

文獻標志碼A

聯系人簡介: 付翠柳, 女, 博士, 副研究員, 主要從事高分子受限輸運行為研究. E-mail: clfu@ciac.ac.cn