基于修正慣用法的水下盾構管片的內力分析

孫波，傅鶴林，張加兵

(1.深圳市地鐵集團有限公司，廣東 深圳 518000；2.中南大學 土木工程學院，湖南 長沙 410075)

基于修正慣用法的水下盾構管片的內力分析

孫波1，傅鶴林2，張加兵2

(1.深圳市地鐵集團有限公司，廣東 深圳 518000；2.中南大學 土木工程學院，湖南 長沙 410075)

摘要:盾構管片設計是一項非常重要的工作，水下盾構由于水文和地質環境更為復雜，要求更為苛刻。傳統方法采用梁—彈簧法。通過采用修正慣用法對水下盾構管片內力進行計算分析。在此基礎上，針對不同接頭剛度、環間剛度的工況作用時，對比分析內力狀況，研究成果可為管片設計提供參考。

關鍵詞：管片設計；修正慣用法；內力；分析

盾構管片內力計算的方法較多，根據不同的計算模型假定，主要有自由變形法、彈性支承法、地層結構法、修正慣用設計法、彈性鉸法及收斂限制法等[1-6]。每種方法都有其適用的范圍，也各有自身的局限性。其中，修正慣用法以其受力明確、計算思路清晰和簡單實用等諸多優點而被廣泛地應用于盾構襯砌設計計算中。黃清飛等[7]利用修正慣用法推導了管片在荷載作用下的彈性解，研究了不同覆土條件下水位變化對管片內力的影響；張美聰[8]運用修正慣用法對圓形盾構隧道襯砌管片內力進行了計算分析；王志良等[9]為研究隧道橫向收斂變形對隧道結構安全的影響，基于彈性極限理論，并結合修正慣用法，求出了螺栓在彈性極限狀態下管片截面的彎矩值；彭益成[4]，曾東洋[10]和夏才初[11]等從數值模擬或理論推導出發，研究了修正慣用法的彎曲剛度有效率η的取值。已有研究表明，利用修正慣用法求解盾構隧道管片內力是行之有效的。基于修正慣用法基本理論，本文擬對水下盾構管片內力進行計算分析，并針對不同接頭剛度、環間剛度的工況作用時，對比分析了內力狀況，為管片設計提供參考。

1修正慣用法理論基礎

修正慣用法是在慣用法的基礎上引入彎曲剛度有效率 η 和彎矩提高率ξ[12～13]。以小于1的剛度折減系數 η來體現環向接頭的影響，不具體考慮接頭的位置，管片環為具有 ηEI 剛度的均質圓環。考慮到管片接頭存在鉸的部分功能，將向相鄰管片傳遞部分彎矩，使錯縫拼裝管片間進行內力重分配，在計算過程中引人小于1.0的彎矩提高率 ξ 來表達錯縫拼裝引起的附加內力值，如圖1所示。計算所選用參數 η 和 ξ 主要根據經驗選取，其荷載計算與慣用法相同。

下面將針對當前管片設計中普遍采用的(修正)慣用法采用結構力學的方法進行理論推導，所采用的計算荷載圖示如圖2所示。

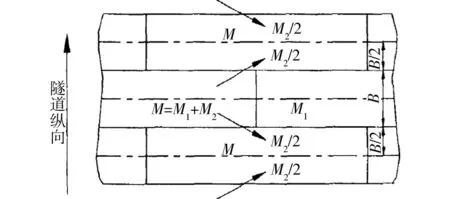
圖1　錯縫拼裝彎曲傳遞及分配示意圖Fig.1 Staggered assembling transmission

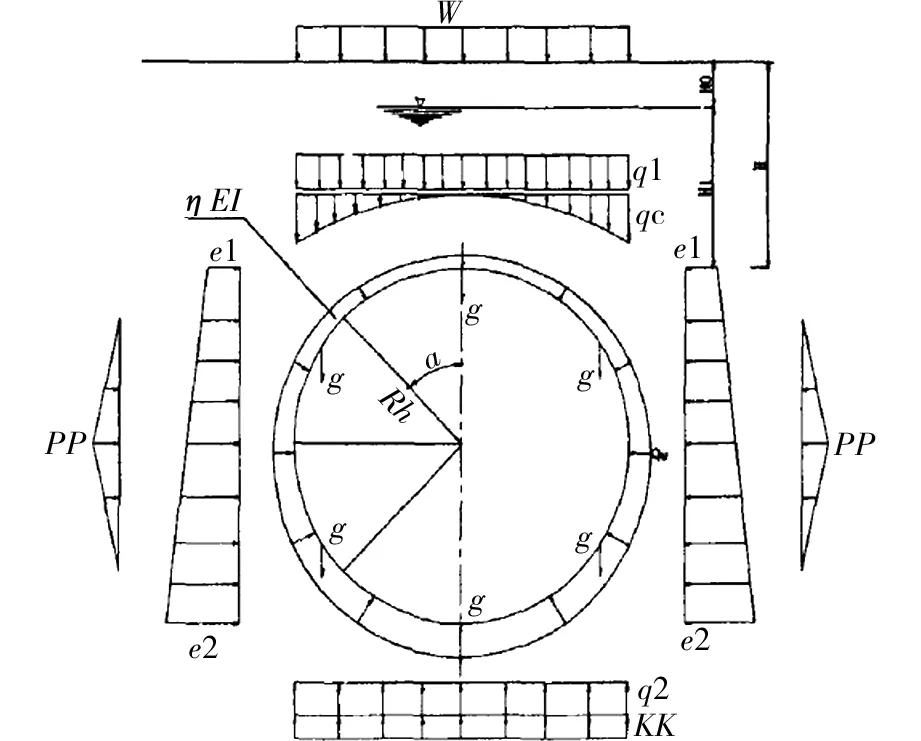
圖2　慣用法的荷載系統Fig.2 Fixed loading system (modified) and distribution diagram of bending

從圖2中可以看出，結構及荷載對稱于豎軸，因此沿對稱面的剪力等于0，故結構為有兩個多余的未知力的超靜定結構。由于豎直對稱軸上的襯砌截面僅豎向下沉，而無水平位移及轉角，故可將圓環底截面視為固定端，同時將未知力X1=0、X2=0移到襯砌環的彈性中心，如圖3所示，因而柔度系數為δ12=0，于是位移協調方程為：

(1)

式中：δ11和δ22分別為柔度系數；Δ1p和Δ2p外荷載產生的位移。

由于軸力和剪力對位移的影響較小，位移主要是彎矩引起的，因此位移計算公式為：

(2)

其中剛度EI 為常數，ds=Rhdφ，由圖3有：

(3)

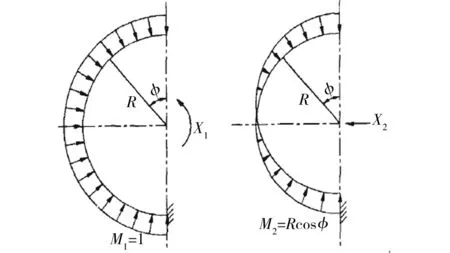
圖3　柔度系數計算簡圖Fig.3 Calculation of flexibility coefficient

將式(3)代入式(1)，求得：

(4)

得到X1和X2后，可求得襯砌中與豎軸成角φ的任一截面的彎矩、軸力及剪力：

(5)

式中：Mp，Np和Qp分別為外荷載所產生的內力。

下面以豎向均布力為例說明計算方法，如圖4，其它荷載的計算原理與此相同，最后對各個荷載采用線性疊加計算出結構最終的內力和變形。

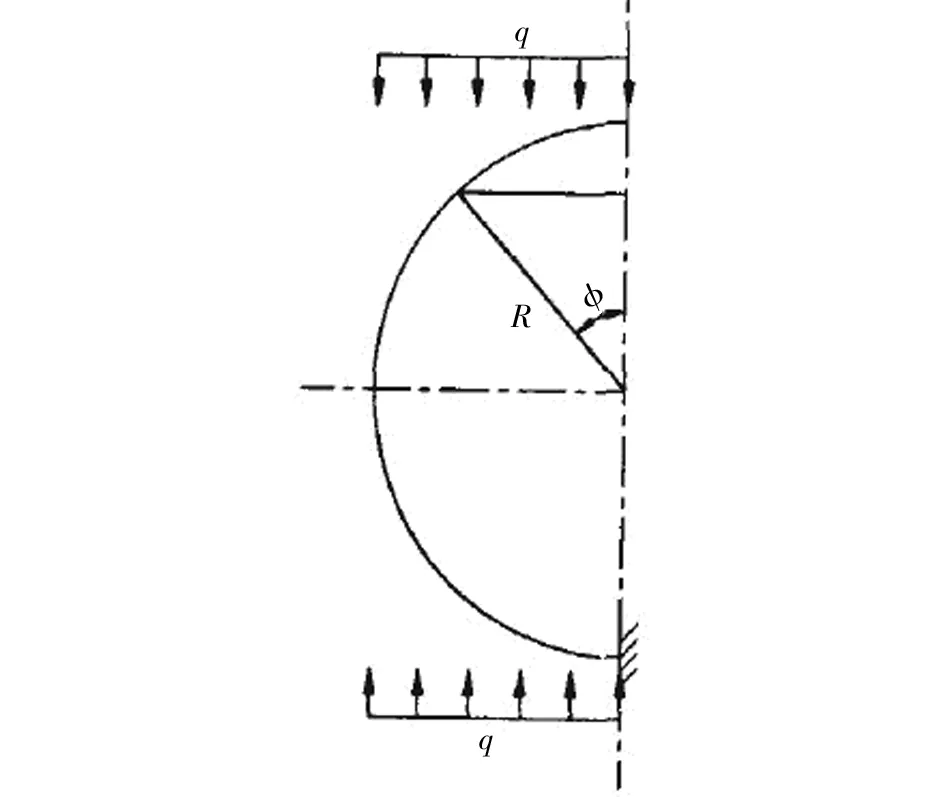
圖4　管片受豎直均布力作用是的結構計算簡圖Fig.4 Lining structure calculation diagram by vertical uniform

(6)

將式(6)代入式(3)可求得：

(7)

將式(7)代入式(5)可求得豎直均布力作用下的內力為：

(8)

同理，可計算其它荷載作用下的Mp，Np，Qp，X1和X2，然后計算得到相應荷載作用下的內力M、N、Q。下面分別給出其它荷載作用下的計算結果：

1)水平均布荷載e：

(9)

2)水平三角形分布荷載△e：

(10)

3)自重g：

(11)

當 0≤φ≤π/2 時：

(12)

當π/2≤φ≤π時：

(13)

4)拱背土壓力：

(14)

當0≤φ≤π/2時：

(15)

當π/2≤φ≤π時：

(16)

式(15)和(16)中：γ (kN/m3)為襯砌環拱背土體的容重。

5)水壓力：

(17)

當 0≤φ≤π/2 時：

(18)

當π/2≤φ≤π時：

(19)式(17)和(18)中：γω(kN/m3)為水的容重；h為水頭。

6)三角形水平地基抗力：

按照(修正)慣用法水平地基抗力的假定，抗力區內任一截面的水平地基抗力為：

(20)

式中：k為地基抗力系數；δ為襯砌環水平直徑點的水平位移；θ為截面與水平直徑的夾角。

由于該荷載與水平直徑呈對稱分布，因此當π/2≤φ≤π時襯砌環內力可按0≤φ≤π/2時的內力計算公式對稱計算，下面給出0≤φ≤π/2時的內力計算公式及0≤φ≤π的地基抗力所產生的彎矩：

(21)

當 0≤φ≤π/4 時：

(22)

當π/4≤φ≤π/2 時：

(23)

當π/2≤φ≤3π/4 時：

(24)

當3π/4≤φ≤π時：

(25)

襯砌環水平直徑點的水平位移 δ可以認為是主動外荷載作用下產生的水平位移 δ1和水平地基反力作用下產生的水平位移 δ2兩部分組成，其值均可由結構力學的力法原理求得。這里僅以豎向均布荷載為例說明計算原理，由于軸力和剪力對變形的影響很小，位移主要由彎曲引起。由上面的推導可知，豎向均布荷載作用下襯砌圓環彎矩可由下式計算得到：

(26)

(27)

同理可求得其它荷載(不考慮襯砌自重和拱背土壓力)及水平地基反力作用下襯砌環水平直徑點的水平位移為：

(28)

由式(28)可計算得到：

(29)

考慮剛度修正，襯砌環水平直徑點的水平位移的計算公式為：

(30)

考慮襯砌自重和拱背土壓力作用時，計算公式可變為：

(31)

2盾構管片內力計算

模型采用管片環外直徑6 000mm，內直徑5 400mm，管片幅寬1 500m，管片厚度250mm。每環襯砌環分為6塊，封頂環為22.5°，其余五環67.5°。荷載見表1。

表1　荷載計算表

表2　各種模型實驗統計

采用均質圓環法得出的最大正彎矩M=285kN·m，對應的軸力為N=1 944kN；最大負彎矩M=263kN·m，對應的軸力N=1 496kN。

2.1國內外管片間抗彎剛度模型

接頭性能對襯砌環的受力和變形有一定影響, 這是襯砌設計中必須考慮的因素。表征接頭性能最重要的參數是接頭抗彎剛度Kθ，它定義為接頭產生單位轉角所需的彎矩。目前，Kθ的取值尚無公式或規范可循，一般是根據接頭受力試驗確定的。對接頭剛度模型研究得到了許多研究者的重視，提出了許多模型，并得到了經驗公式，見表2。

1)張厚美等[14]在《圓形隧道裝配式襯砌接頭剛度模型研究》中得出在接頭構造、螺栓預緊力等確定的條件下，接縫轉角θ只與軸力N和彎矩M有關，可用回歸分析方法得到θ與M和N的關系。

θ=b0+b1M+b2N+b3MN

(32)

(33)

式中：M為彎矩，kN·m；N為軸力，kN；Kθ為接頭抗彎剛度，kN·m/rad。b0，b1，b2和b3為回歸系數，見表3。

表3接頭剛度模型回歸系數及統計值

Table3Jointstiffnessmodelofregressioncoefficientsandthestatisticalvalue

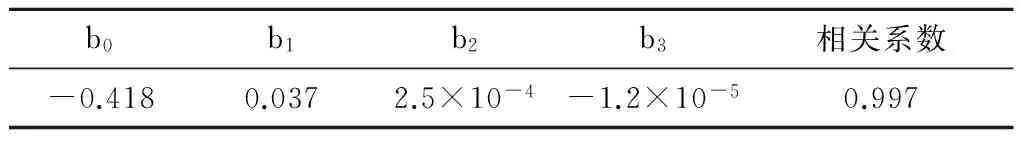
b0b1b2b3相關系數-0.4180.0372.5×10-4-1.2×10-50.997

2)周海鷹、陳廷國、李立新[15]在《地鐵區間盾構隧道襯砌縱向接頭抗彎剛度試驗研究》中考慮不同的偏心距、預壓力和襯墊尺寸后做了一系列模型實驗，提出了經驗公式：

(34)

式中：k1，k2，k3和k4為回歸系數，其單位分別為kN·m/rad，kN·m/rad，kN·m，kN·m/rad和kN·m/rad2。取值見表4。

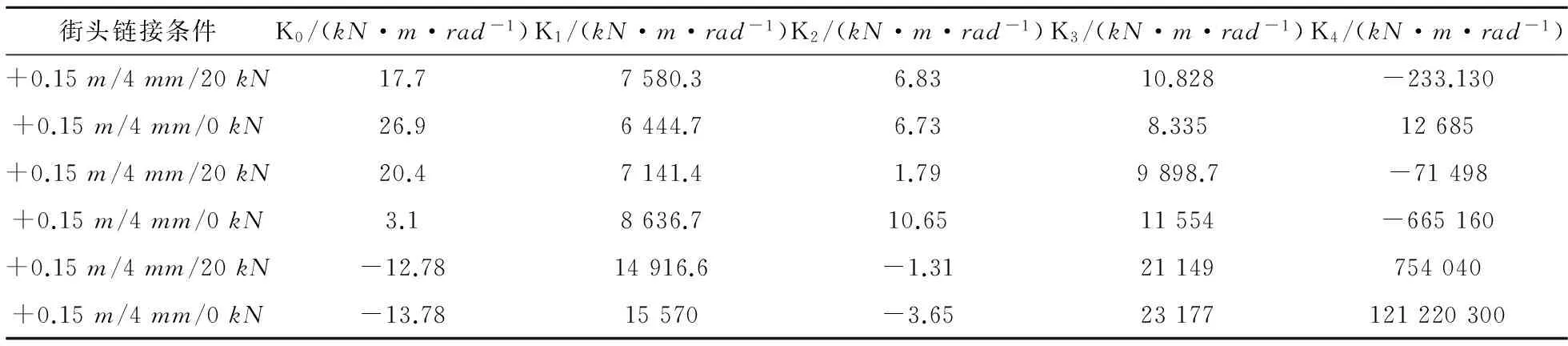
表4　不同條件下接頭轉角與彎矩試驗數據擬合結果

3)曾東洋、何川[16]在《地鐵盾構隧道管片接頭抗彎剛度的數值計算》中提出的經驗公式為：

正彎曲：

負彎曲：

式中：彎矩M的單位為kN·m;軸力N的單位為MN;轉角θ的單位為10-5rad。

2.2管片間抗彎剛度取值

由于周海鷹、陳廷國、李立新在《地鐵區間盾構隧道襯砌縱向接頭抗彎剛度實驗研究》中提出的經驗公式只是列舉了幾種偏心距、襯墊尺寸、預壓力下的經驗公式，本文選取另外兩種模型實驗的經驗公式進行對比。

1)將均質圓環法求出的彎矩與軸力代入張厚美在文獻《圓形隧道裝配式襯砌接頭剛度模型研究》提出的公式得：

正彎矩處：

=7.2×104kN·m/rad

負彎矩處：

=5.3×104kN·m/rad

2)將均質圓環法求出的彎矩與軸力代入曾東洋、何川在文獻《地鐵盾構隧道管片接頭抗彎剛度的數值計算》中提出的經驗公式得：

正彎矩處：

=4.82×104kN·m/rad

負彎矩處：

=3.48×104kN·m/rad

參照國內外有關試驗研究結果，接頭抗彎剛度的值通常為104～105kN·m/rad，按2種經驗公式計算得到的接頭抗彎剛度都在這一范圍內，所以都是可行的。而張厚美模型實驗提出的經驗公式相對簡單明了，因而采用其計算得出的數值用于模型計算

環間彈簧徑向剛度取為彈簧的抗壓剛度786 000kN/m，環間彈簧切向剛度取為彈簧的剪切剛度114 900kN/m。

2.3修正慣用法模擬計算

彈簧的剛度取值算好后，用修正慣用法來進行模擬。梁—彈簧模型中的彈簧形式可見圖5。在修正管用法中分別取η=0.8、ξ=0.8，計算模型見圖6。

計算結果見圖7。從圖中可得到用修正慣用法計算得到的最大正彎矩是258.314kN·m，最大負彎矩為240.322kN·m。對比分析文獻[14]，可看出用修正慣用法得出的設計彎矩比梁-彈簧模型得到的值要大，因此采用修正慣用法進行管片設計是安全的。

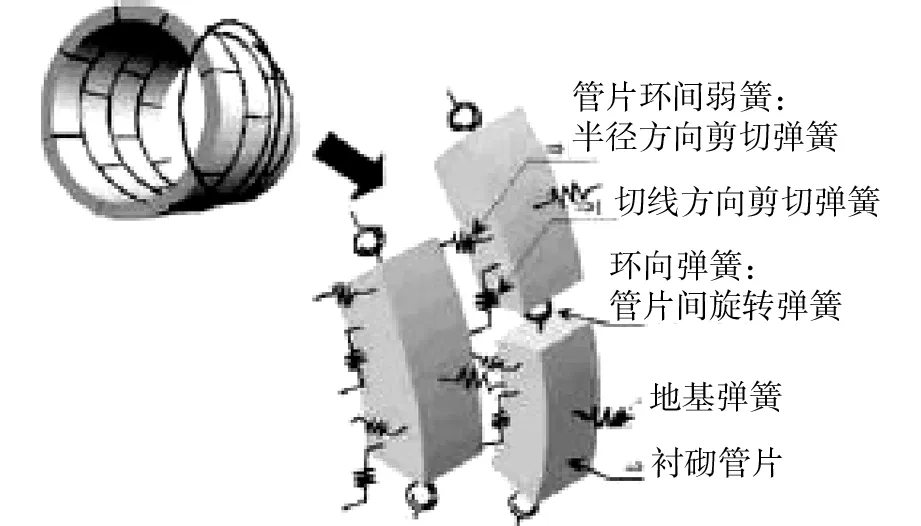
圖5　梁-彈簧模型中的彈簧形式Fig.5 Spring beam spring model

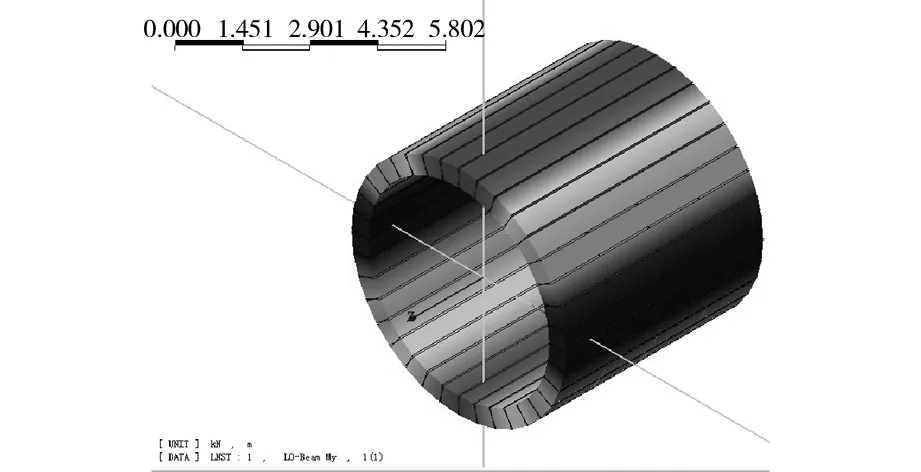
圖6　修正慣用法模型Fig.6 Fixed usage model

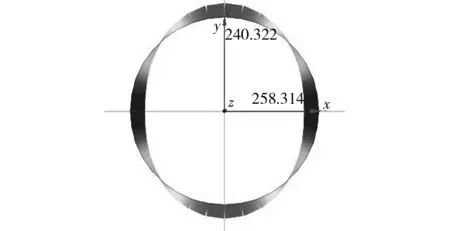
圖7　修正慣用法的彎矩圖Fig.7 Bending moment diagram of the modified routine method

3計算結果分析

3.1不同接頭抗彎剛度的計算結果

為分析不同管片間接頭抗彎剛度下襯砌結構的力學特性，將接頭力學基本參數中的管片間接頭抗彎剛度按一定范圍進行變化。計算時環間剛度不變，將抗彎剛度按0.167，0.33，0.67，1，1.33，1.67和2倍進行變化。具體計算結果見表5。不同接頭抗彎剛度對比分析如下：

表5不同接頭抗彎剛度下內力變化表

Table5Theflexuralrigidityoftheinternalforceunderthechangesofdifferentjointsurface

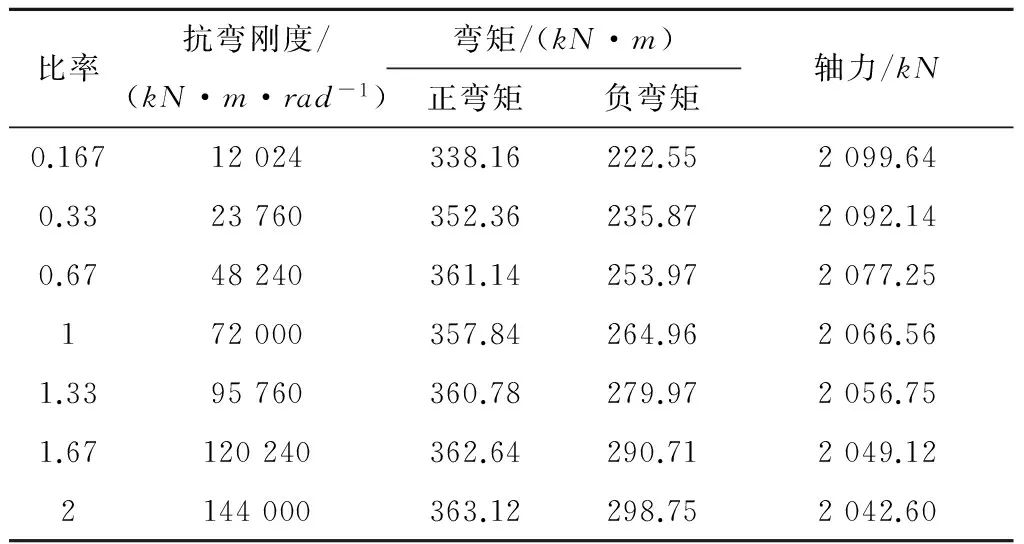
比率抗彎剛度/(kN·m·rad-1)彎矩/(kN·m)正彎矩負彎矩軸力/kN0.16712024338.16222.552099.640.3323760352.36235.872092.140.6748240361.14253.972077.25172000357.84264.962066.561.3395760360.78279.972056.751.67120240362.64290.712049.122144000363.12298.752042.60

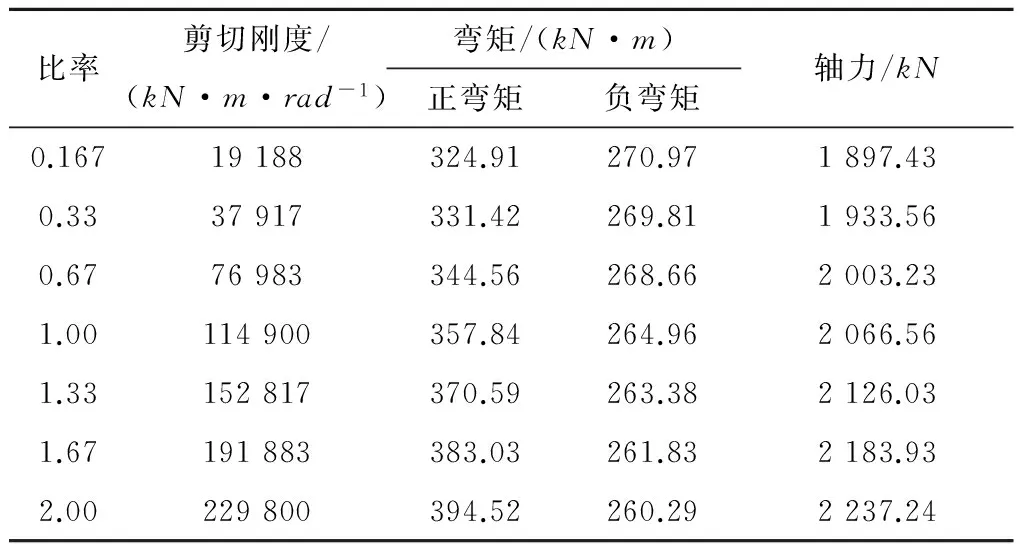
表6　不同環間剪切剛度下內力變化表

1)在荷載和管片襯砌結構條件完全相同的情況下，隨著管片間接頭抗彎剛度的增大，襯砌環軸力最大值在逐漸變小，但是變化的幅度都不大。在管片間接頭抗彎剛度變化范圍內(Kθ=12 024～144 000kN·m/rad)，軸力最大值減小不到3%。究其原因，主要是在土體自重作用下，管片僅承受壓力，因而管片間接頭抗彎剛度對軸力的影響不大。

2)管片間接頭抗彎剛度對襯砌環彎矩的影響較大。在相同條件下，隨著管片間接頭抗彎剛度增大，襯砌環彎矩最大值和最小值都增大，最大負彎矩逐漸增大，近于線性關系，而襯砌環最大正彎矩增大，抗彎剛度小時變化較大，繼而趨勢變小，最后近于線性。在管片間接頭抗彎剛度變化范圍內，襯砌環負彎矩最大值增大了7.4%，而正彎矩最大值增大了34.2%。管片間接頭抗彎剛度對管片環彎矩影響最大的部位是在封頂塊位置，隨著管片間接頭抗彎剛度的增大該部位的彎矩最大值區域顯著增大。

3)在彈簧接頭剛度很小的情況下，接頭處彎矩并不趨于0，這是因為在錯縫的條件下由于錯縫效應存在，彎矩并不是全部都經由管片接頭傳遞，其一部分是利用環間接頭縱向螺栓的剪切阻力傳遞給錯縫拼裝起來的鄰接管片。

3.2不同環間剛度的計算結果

計算時接頭抗彎剛度不變，將環間剪切剛度按0.167，0.33，0.67，1，1.33，1.67和2倍進行變化。具體計算結果見表6。不同環間剛度對比分析如下：

1)在荷載和管片襯砌結構條件完全相同的情況下，隨著管片環間剪切剛度的增大，襯砌環軸力最大值在逐漸變大。

2)在相同條件下，隨著管片環間剪切剛度的增大，襯砌環最大負彎矩逐漸減小，近于線性關系，但是影響較小，變化僅4%；襯砌環最大正彎矩逐漸增大，在環間剪切剛度小時，變化小，隨著環間剪切剛度的增大，變化趨勢增大，最后近于線性。管片環間剪切剛度對最大正彎矩影響較大，變化了21.4%。

4結論

1)采用修正慣用設計法計算模型簡單，在設計過程中只要彎曲剛度有效率η及彎矩增大率ξ通過試驗結果和工程類比，取值合理，計算結果是完全能滿足工程需要的；

2)針對不同接頭剛度、環間剛度的工況作用時，對比分析了內力狀況，本文的研究成果可為管片設計提供了參考。

參考文獻：

[1] 郭璇，孫文波，張曉新，等．地下圓形隧道自由變形法的力法推導及例證[J]．鐵道學報，2014，36(9)：85-91.

GUOXuan,SUNWenbo,ZHANGXiaoxin,etal.DeductionandexampleillustrationofcalculationstructuralmechanicsforcesofundergroundpressurearchliningwithFFDnethod[J].JournaloftheChinaRailwaySociety, 2014，36(9)：85-91.

[2] 姚超凡，晏啟祥，何川，等．地下圓形隧道自由變形法的力法推導及例證[J]. 鐵道標準設計, 2013(12)：95-99.

YAOChaofan,YANQixiang,HEChuan,etal.Comparativestudyoninternalforceanalysismethodsofshieldtunnel[J].RailwayStandardDesign, 2013(12)：95-99.

[3] 丁文其，朱令，彭益成，等．基于地層-結構法的沉管隧道三維數值分析[J]. 巖土工程學報, 2013, 35(增2)：622-626.

DINGWenqi,ZHULing,PENGYicheng,etal. 3Dnumericalanalysisofimmersedtunnelsbasedonstratum-structuremethod[J].ChineseJournalofGeotechnicalEngineering, 2013, 35(Suppl2)：622-626.

[4] 彭益成，丁文其，閆治國，等．修正慣用法中彎曲剛度有效率的影響因素分析及計算方法[J]. 巖土工程學報, 2013, 35(增1)：496-500.

PENGYicheng,DINGWenqi,YANZhiguo,etal.Analysisandcalculationmethodofeffectivebendingrigidityratioinmodifiedroutinemethod[J].ChineseJournalofGeotechnicalEngineering, 2013, 35(Suppl1)：496-500.

[5] 丁軍霞，馮衛星，張保儉．盾構隧道管片襯砌內力計算[J]. 石家莊鐵道學院學報, 2004, 17(2)：66-69.

DINGJunxia,FengWeixing,ZhangBaojian.Internalforcecalculationofshieldtunnelsegment[J].JournalofShijiazhuangRailwayInstitute, 2004, 17(2)：66-69.

[6] 張常光，趙均海，張慶賀．基于統一強度理論的深埋圓形巖石隧道收斂限制分析[J]. 巖土工程學報, 2012, 34(1)：110-114.

ZHANGChangguang,ZHAOJunhai,ZHANGQinghe.Convergence-confinementanalysisofdeepcircularrocktunnelsbasedonunifiedstrengththeory[J].ChineseJournalofGeotechnicalEngineering, 2012, 34(1)：110-114.

[7] 黃清飛，袁大軍，王夢恕．水位對盾構隧道管片結構內力影響研究[J]. 巖土工程學報, 2008, 30(8)：1112-1120.

HUANGQingfei,YUANDajun,WANGMengshu.Influenceofwaterleveloninternalforceofsegmentsofshieldtunnels[J].ChineseJournalofGeotechnicalEngineering, 2008, 30(8)：1112-1120.

[8] 張美聰．圓形盾構隧道襯砌管片的計算分析[J]. 現代隧道技術, 2009, 46(5)：23-27.

ZHANGMeicong.Analysisofliningsegmentsforcircularshieldtunnels[J].ModernTunnellingTechnology, 2009, 46(5)：23-27.

[9] 王志良，申林方，劉國彬．基于彈性極限理論的盾構隧道收斂變形研究[J]. 鐵道學報, 2012, 34(2)：100-103.

WANGZhiliang,SHENLinfang,LIUGuobin.Researchonconvergencedeformationofshieldtunnelwithelasticlimittheory[J].JournaloftheChinaRailwaySociety, 2012, 34(2)：100-103.

[10] 曾東洋，何 川．地鐵盾構隧道管片接頭抗彎剛度的數值計算[J]. 西南交通大學學報, 2004, 22(6)：744-748.

ZENGDongyang,GHEChuan.Numericalsimulationofsegmentjointbendingstiffnessofmetroshieldtunnel[J].JournalofSouthwestJiaotongUniversity, 2004, 22(6)：744-748.

[11] 夏才初，曾格華，卞躍威．盾構隧道管片環縱向接頭抗彎剛度值的不動點迭代確定方法[J]. 巖石力學與工程學報, 2014, 33(5)：991-912.

XIACaichu,ZENGGehua,BIANYuewei.Methodfordeterminingbendingstiffnessofshieldtunnelsegmentringslongitudinaljointbasedonfix-pointiteration[J].ChineseJournalofRockMechanicsandEngineering, 2014, 33(5)：991-912.

[12] 侯公羽，楊 悅，劉 波．盾構管片設計改進慣用法模型及其內力解析解[J]. 巖土力學, 2008, 29(1)：161-166.

HOUGongyu,YANGYue,LIUBo.Improvedjointmodelwithroutinemethodandananalyticalsolutionofitsinnerforces[J].RockandSoilMechanics, 2008, 29(1)：161-166.

[13] 黃昌富．盾構隧道通用裝配式管片襯砌結構計算分析[J]. 巖土力學, 2003, 25(3)：322-325.

HUANGChangfu.Analysisandcomputationonuniversalassemblingsegmentliningforshieldtunnel[J].RockandSoilMechanics, 2003, 25(3)：322-325.

[14] 張厚美，過 遲，付德明．圓形隧道裝配式襯砌接頭剛度模型研究[J]. 巖土工程學報, 2000, 22(3)：309-313.

ZHANGHoumei,GUOChi,FUDeming.Astudyonthestiffnessmodelofcirculartunnelprefabricatedlining[J].ChineseJournalofGeotechnicalEngineering, 2000, 22(3)：309-313.

[15] 周海鷹，陳廷國，李立新．地鐵區間盾構隧道襯砌縱向接頭抗彎剛度試驗研究[J]. 工業建筑, 2010, 40(7)：59-62.

ZHOUHaiying,CHENTingguo,LILixin.Studyonjointbendingstiffnessandinfluencingfactorsofmetroshieldtunnelinglining[J].IndustrialConstruction, 2010, 40(7)：59-62.

[16] 曾東洋，何 川．地鐵盾構隧道管片接頭剛度影響因素研究[J]. 鐵道學報, 2005, 27(4)：90-95.

ZENGDongyang,HEChuan.Studyonfactorsinfluentialinmetroshieldtunnelsegmentjointbendingstiffness[J].JournaloftheChinaRailwaySociety, 2005, 27(4)：90-95.

Internal force analysis of underwater shield segment based on modified routine method

SUN Bo1，FU Helin2，ZHANG Jiabing2

(1.ShenzhenMetroGroupCo.,Ltd.Shengzhen518000,China;2.SchoolofcivilEngineering,CentralSouthUniversity,Changsha410075,China)

Abstract:The design of shield segment is a very important task. Moreover, underwater shield is more demanding because the hydrological and geological environments are more complex. The traditional method of internal force analysis of shield segment was the beam-spring method. Internal forces of shield segment under water were analyzed with the modified routine method in this study. According to the condition of rigidity of joints between different ring configurations, comparison and analysis of the internal force status were presented. The research findings presented in this paper can provide useful references for the design of similar shield segments.

Key words：segment design; modified routine method; internal force; analysis

收稿日期：2015-11-12

基金項目：國家自然科學基金資助項目(51578500/E080506);國家自然科學重點基金資助項目(51538009)

通訊作者：傅鶴林(1965-)，男，江西人，教授，從事隧道、巖土工程學研究工作；E-mail：517336864@qq.com

中圖分類號：TU 471.8

文獻標志碼：A

文章編號：1672-7029(2016)05-0929-09