基于自定義本構模型的盾構隧道開挖面極限支護力研究

黃阜，李在藍，朱亮，楊歡

(1.長沙理工大學 土木與建筑學院，湖南 長沙 410114；2.長沙理工大學 橋梁工程安全控制技術與裝備湖南省工程技術研究中心，湖南 長沙 410114)

基于自定義本構模型的盾構隧道開挖面極限支護力研究

黃阜1,2，李在藍1，朱亮1，楊歡1

(1.長沙理工大學 土木與建筑學院，湖南 長沙 410114；2.長沙理工大學 橋梁工程安全控制技術與裝備湖南省工程技術研究中心，湖南 長沙 410114)

摘要:為了分析巖土體的非線性破壞特性對盾構隧道的開挖面極限支護力的影響，利用FLAC3D提供的二次開發(fā)平臺，開發(fā)基于非線性Mohr-Coulomb破壞準則的自定義本構模型。調用該本構模型對盾構隧道的施工過程進行數(shù)值模擬，得到非線性M-C破壞準則作用下盾構隧道開挖面極限支護力的數(shù)值解。利用切線法將非線性Mohr-Coulomb破壞準則引入上限分析的能耗計算中，獲得非線性破壞準則作用下盾構隧道開挖面支護力的上限解。通過將數(shù)值解和上限解進行對比，證明采用自定義本構模型計算的盾構隧道開挖面極限支護力是正確的。

關鍵詞：開挖面極限支護力；非線性破壞準則；數(shù)值模擬；極限分析上限定理

自20世紀60年代我國開始籌備地鐵建設至今，地鐵建設在我國已經(jīng)歷了半個世紀的發(fā)展歷程。由于地鐵具備快速、環(huán)保、安全的優(yōu)點，被視為解決城市交通擁堵和大氣污染等問題的有效途徑。因此，地鐵成為目前我國基礎設施建設中的熱點項目，各大城市都在積極規(guī)劃建設以地鐵為主體的城市軌道交通體系。為了保證地鐵區(qū)間隧道的開挖能夠在確保安全的前提下滿足工期要求，大部分地鐵區(qū)間隧道都采用盾構法進行施工。盾構隧道掘進過程中，必須在開挖面上施加一個合理的支護力以保證盾構機平穩(wěn)、安全地推進。當隧道開挖面即將發(fā)生失穩(wěn)破壞時，作用在開挖面上的臨界支護力被稱為極限支護力。確定極限支護力可以為實際掘進過程中開挖面支護力大小的選擇和優(yōu)化提供依據(jù)。因此，盾構隧道開挖面極限支護力的研究也就成為了盾構隧道穩(wěn)定性研究中的一個熱點問題，國內(nèi)外已經(jīng)有許多學者采用各種方法對這一課題進行了卓有成效的研究。

黃正榮等[1]基于數(shù)值模擬技術，根據(jù)盾構隧道開挖面水平位移隨支護力變化的關系，提出了開挖面極限支護力的確定方法，并利用這一方法研究了地下水位和土層參數(shù)對極限支護力的影響。隨后，高健等[2]采用極限平衡法結合數(shù)值模擬技術對滲透力作用下的盾構隧道開挖面穩(wěn)定性進行了研究。王浩然等[3]利用有限元軟件，分析了盾構隧道滲流條件下的開挖面破壞模式，并在此基礎上構建了開挖面的上限破壞機制，得到了滲流條件下開挖面支護力的上限解。鄭永來等[4]通過構建高水壓作用下的隧道開挖面破壞機制，得到了開挖面極限支護力的上限解，為越江盾構隧道支護力的確定提供了依據(jù)。Salvador等[5]在前人的研究基礎上構建了一種曲線型破壞機制，在通過數(shù)值模擬技術驗證了這種破壞機制的有效性之后，他們用這種破壞機制計算了盾構隧道在分層土中掘進時所需要的開挖面極限支護力。

上述針對盾構隧道開挖面極限支護力的研究都是基于線性的破壞準則進行的。然而，大量已有研究成果表明，巖土材料在破壞時，最大和最小主應力的變化遵循非線性關系。在實際工程中，采用線性破壞準則對巖土體進行研究有可能會低估土工結構的位移，因此許多學者開始采用非線性破壞準則對邊坡[6-7]，地基承載力[8]，錨板[9]和土壓力[10]等巖土構筑物的穩(wěn)定性問題進行研究。然而，目前在相關研究中還未見采用非線性Mohr-Coulomb破壞準則構建的自定義本構模型對土工構筑物穩(wěn)定性進行數(shù)值模擬的報導。因此，本文首次開發(fā)了基于非線性Mohr-Coulomb破壞準則的自定義本構模型，并通過在盾構隧道掘進的數(shù)值模擬過程中調用該本構模型，得到了非線性破壞準則作用下的盾構隧道開挖面極限支護力。然后采用極限上限法計算了盾構隧道開挖面極限支護力的上限解，通過將數(shù)值解和上限解進行對比分析，證明了將自定義本構模型應用于盾構隧道開挖面極限支護力研究的有效性。

1非線性Mohr-Coulomb本構模型

1.1非線性Mohr-Coulomb破壞準則

Agar等[11]在不同的側限條件下對油砂進行了三軸試驗，試驗結果表明該砂土在破壞時，最大和最小主應力之間的非線性關系可以用下式表示：

(1)

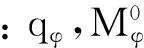
(2)其中，c0，σt和m均為土體參數(shù)，可由三軸試驗確定。1.2非線性Mohr-Coulomb本構模型的力學方程

由于非線性Mohr-Coulomb破壞準則是一個描述最大和最小主應力之間關系的冪指數(shù)型非線性函數(shù)，而廣義Hoek-Brown破壞準則同樣采用了冪指數(shù)型非線性函數(shù)表示最大、最小主應力之間的關系。因此，根據(jù)FLAC說明手冊中Hoek-Brown本構模型的開發(fā)過程[12]，得到了用于編程的非線性M-C本構模型的力學表達式。

1.2.1基本方程

初始應力可以由彈性增量理論計算得到：

(3)

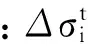
(4)

此本構模型得到的最終應力與應變增量的彈性分量有關，由此得到：

(5)

(6)

假設模型遵循如下流動法則：

(7)

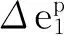
(8)

模型發(fā)生屈服時的最終應力關系式為：

(9)

1.2.2流動法則

根據(jù)相關聯(lián)流動法則，塑性應變率矢量應該與屈服面正交，因此：

(10)

將式(3)代入式(4)，得到了主應變增量的塑性分量，將其代入式(7)，得到：

(11)

2非線性Mohr-Coulomb本構模型在FLAC中的開發(fā)

2.1基于非線性Mohr-Coulomb破壞準則的自定義本構模型開發(fā)流程

本文利用FLAC二次開發(fā)平臺VC++將非線性Mohr-Coulomb破壞準則的力學關系式嵌入到FLAC自帶的本構模型的源程序中，然后生成動態(tài)鏈接庫文件(.DLL文件)。將此文件加載到FLAC程序安裝文件的根目錄下，并在主程序中添加相應的調用語句，則可以隨時在計算過程中根據(jù)用戶指令對此本構模型進行調用。此外，用戶自定義的本構模型在調用過程中與FLAC中內(nèi)置的本構模型處于同一個優(yōu)先級，因此采用自定義本構模型的計算效率和采用內(nèi)置本構模型的計算效率一致。

2.2開發(fā)的編程概要

為了方便用戶進行二次開發(fā)，F(xiàn)LAC軟件向用戶提供了內(nèi)置本構模型的C++源代碼，因此自定義本構模型可以在軟件內(nèi)置本構模型的上進行修改，而無需重新編寫一個完整的自定義本構模型源程序。根據(jù)陳育民和劉漢龍[13]開發(fā)鄧肯-張自定義本構模型的經(jīng)驗，本文在H-B本構模型的基礎上將非線性M-C破壞準則的力學關系嵌入到FLAC內(nèi)置的本構模型中，得到了基于非線性M-C破壞準則的自定義本構模型。自定義本構模型源程序編寫的主要內(nèi)容包括對內(nèi)置本構模型頭文件(.h)和源文件(.cpp)的修改[14]。為方便敘述，本文將自定義的本構模型命名為NonModel。

將頭文件處理過程如下：

1)定義枚舉函數(shù)ModelNum中的模型編號，由于FLAC軟件中內(nèi)置的模型較多，為避免重復，一般將模型編號取大于100。將調用模型函數(shù)以及打印輸出函數(shù)中的本構模型名稱均改為NonModel。

2)定義private中的私有變量。私有變量一般包括模型本身所需要的參數(shù)以及理論敘述中所使用的關鍵變量。考慮自定義本構模型的實際情況，將模型中的參數(shù)和重要中間變量寫入其中。

編寫源文件主要內(nèi)容如下：

1)通過C++程序的查找功能找出源文件中含有原本構模型名稱的語句并全部替換為NonModel。

2)按照頭文件中的私有變量對ConstitutiveModel()函數(shù)進行相應的修改，并對頭文件的私有變量賦值，通常賦值為0。

3)在properties()函數(shù)中依次將自定義本構模型的參數(shù)編寫在其中，并按相同的順序把參數(shù)寫入Getproperties()函數(shù)與Setproperties()函數(shù)以及Copy()函數(shù)中。

4)根據(jù)自定義的本構模型特點，定義Initialize()函數(shù)中的關鍵中間變量，本函數(shù)的變量均與σ3無關，與σ3相關的變量全部寫入Run()函數(shù)中。

5)確定Run()函數(shù)是整個編程中的重點與難點，其中最關鍵的步驟是對材料破壞準則與屈服函數(shù)的修改，具體實現(xiàn)過程依據(jù)前述的非線性M-C本構模型的數(shù)學表達式進行。

3基于非線性本構模型的盾構隧道開挖面極限支護力

3.1盾構隧道開挖面極限支護力的確定

為了計算非線性破壞準則作用下的盾構隧道開挖面極限支護力，利用FLAC3D構建了盾構隧道的模型，如圖1所示。隧道直徑6m，埋深20m，上邊界取至地面，下邊界取至隧道底部以下12m，橫向邊界取隧道兩側22m，隧道縱向長度為40m。將前述自定義本構模型的動態(tài)鏈接庫文件復制到FLAC3D程序安裝文件的根目錄下，并在主程序中對這個自定義本構模型進行調用，實現(xiàn)非線性本構模型作用下盾構隧道開挖過程的模擬。

計算過程中，隧道一次性開挖20m，已經(jīng)開挖的斷面上立即施做拼裝式管片襯砌，同時在開挖面上施加水平向前的支護力，并記錄開挖面中心點處的水平位移。黃正榮等[1]認為，開挖面支護力不足將導致開挖面發(fā)生向盾構機壓力艙的水平位移。因此，可以通過研究支護力和開挖面水平位移的關系得到開挖面的極限支護力。計算表明，開挖面的水平位移會隨支護力的減小而逐漸增大，當支護力減小到某一臨界點的時候，開挖面水平位移的增幅會突然變大，導致開挖面發(fā)生失穩(wěn)破壞。當土體參數(shù)σt=24.7kPa，c0=10kPa，m=1.1，γ=20kN/m3時，將不同支護力對應的開挖面中心點最大水平位移記錄下來，繪制成曲線圖，如圖2所示。從圖中可以發(fā)現(xiàn)，當支護力減小到36.5kPa的時候，開挖面水平位移曲線出現(xiàn)了一個拐點，如果支護力繼續(xù)減小，水平位移急劇增大導致計算不能收斂。可以認為，這個拐點對應的支護力就是維持開挖面穩(wěn)定的極限支護力。

圖1　盾構隧道模型Fig.1 Model of shield tunnel

圖2　隧道開挖面支護力與中心點最大水平位移關系圖Fig.2 Relationship between support pressure of tunnel face and the maximal horizontal displacement of center point for tunnel face

4驗證計算

4.1基于非線性破壞準則的盾構隧道開挖面支護力上限解

極限分析上限定理利用構建的機動許可速度場中外力功率和內(nèi)能耗散功率的關系推導出所研究問題的上限目標函數(shù)，然后通過優(yōu)化計算得到該問題的最優(yōu)上限解。由于上限法無需通過繁瑣的彈塑性力學分析即可得到一個接近真實解的極限荷載，因而被許多學者用于盾構隧道開挖面的極限支護力研究[3, 15, 16]。為了得到主動破壞模式下盾構隧道開挖面支護力的上限解，許敬叔等[17]利用對數(shù)螺旋線構建了一種曲線型破壞機制。這種雙對數(shù)螺旋線的開挖面破壞機制由兩條對數(shù)螺旋線AE和BE從隧道的頂端和底部延伸到開挖面上方的土層中，交匯于E點，形成一個曲線型的二維塌落體ABE，如圖3所示。O點為這個塌落體的旋轉中心，該塌落體繞O點以一定的角速度ω轉動。此塌落體和開挖面前方未發(fā)生位移的土體之間發(fā)生相對滑動，導致在螺旋線AE和BE上由于摩擦產(chǎn)生能量損耗，從而可以利用外力功率和損耗功率求解支護力的上限解。

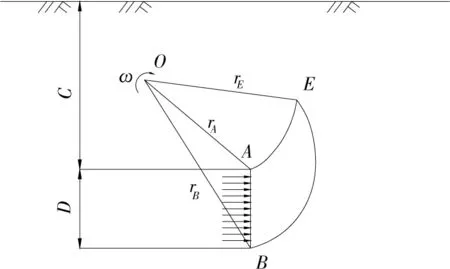
圖3　隧道開挖面對數(shù)螺旋線型破壞機制Fig.3 Logarithmic spiral failure mechanism of tunnel face

然而，許敬叔等[17]的解答是基于線性M-C破壞準則進行的，沒有考慮土體非線性破壞特性對支護力上限解的影響。為了得到非線性破壞準則作用下的隧道開挖面支護力上限解，基于上述對數(shù)螺旋線型破壞機制，本文采用切線法[18-19]將非線性破壞準則引入上限定理的能耗計算過程中，得到非線性破壞準則作用下的開挖面支護力上限表達式。然后利用序列二次規(guī)劃算法對該上限表達式進行優(yōu)化計算，最終得到開挖面支護力的最優(yōu)上限解。

圖4　M-C非線性破壞準則中的切線法Fig.4 Generalized tangential technique for M-C nonlinear failure criterion

切線法可以闡述如下：在非線性破壞準則的強度包絡線上任一點M處作一條切線，則此切線在縱軸上的截距ct和其對應的傾角φt可以視為與線性破壞準則下c和φ等價的參數(shù)代入能耗計算中。圖4中任一點的切線方程可由下式表示：

τ=ct+σn·tanφt

(12)

而ct和tanφt的表達式如下：

(13)

(14)

式中：c0，σt和m等參數(shù)的含義與式(2)中所示的參數(shù)一致。由于切線法中經(jīng)過強度包絡線M點的切線是任意的，因此在上限計算過程中，將φt視為一個變量代入上限破壞機制的能耗方程中，通過優(yōu)化計算可以得到最優(yōu)上限解對應的φt值和對應的切線方程。

計算開挖面支護力σT的上限解，首先要計算破壞機制中的外力功率Pe和內(nèi)能耗散功率Pv，其中外力功率Pe由土體重力功率Pγ和支護力功率PT組成。利用積分運算，可以得到上述各功率的解析表達式，然后根據(jù)虛功率方程，得到隧道開挖面支護力σT上限解的表達式：

(15)

式中：ω為機動速度場中速度間斷面繞旋轉中心O點轉動的角速度；rB為B到O點的距離；f是一個以旋轉角θ為變量的函數(shù)。將式(15)視為一個目標函數(shù)，采用序列二次規(guī)劃算法編制程序搜索該函數(shù)在滿足相應約束條件的情況下的最大值，得到非線性破壞準則作用下的最優(yōu)上限解。

4.2開挖面支護力數(shù)值解和上限解對比分析

為了驗證本文采用數(shù)值模擬計算的盾構隧道開挖面支護力的正確性，將數(shù)值模擬結果和上限解進行對了比分析。利用前面所敘述的方法，當盾構隧道直徑D=6m，埋深C=20m，土體參數(shù)σt=24.7kPa，c0=10kPa，γ=20kN/m3，非線性參數(shù)m=1.1～1.5時，分別計算了開挖面支護力的數(shù)值解和上限解，如下表所示：

表1開挖面支護力數(shù)值解和上限解對比

Table1Comparisonofnumericalsolutionandupperboundsolutionofsupportpressurefortunnelface

支護力σTm值1.11.21.31.41.5數(shù)值解/kPa36.545566982上限解/kPa40.550.2761.774.2387.91差值9.88%10.48%9.24%7.05%6.72%

圖5　盾構隧道開挖面支護力σT隨非線性參數(shù)m變化規(guī)律Fig.5 Variation law of support pressure σT for tunnel face with nonlinear parameter m

從上表中可以看出，本文計算的數(shù)值解和上限解比較吻合，最大差值為10.48%。此外，圖5所示的支護力隨非線性參數(shù)變化規(guī)律表明，支護力數(shù)值解和上限解隨非線性參數(shù)的變化趨勢相同，都隨m值的增大而增大。數(shù)值解和上限解的一致性，證明利用本文所開發(fā)的自定義本構模型對盾構隧道開挖面極限支護力進行求解這一方法是正確和有效的。

5結論

1)根據(jù)非線性Mohr-Coulomb破壞準則的力學關系，利用FLAC3D提供的二次開發(fā)平臺，開發(fā)了基于非線性M-C破壞準則的自定義本構模型。調用該本構模型，對盾構隧道的開挖進行數(shù)值模擬，得到了非線性M-C破壞準則作用下隧道開挖面的極限支護力。

2)采用切線法將非線性M-C破壞準則引入極限分析上限定理的能耗計算，獲得了非線性M-C破壞準則作用下的盾構隧道開挖面支護力上限解。將數(shù)值模擬解和上限解進行了對比，結果表明，兩者十分吻合，證明本文采用自定義本構模型計算得到的盾構隧道開挖面極限支護力是正確的。

3)參數(shù)分析表明，基于自定義本構模型計算的隧道開挖面的極限支護力，隨非線性參數(shù)m的增大而增大。

參考文獻：

[1] 黃正榮，朱偉，梁精華，等. 盾構法隧道開挖面極限支護壓力研究[J]. 土木工程學報， 2006， 39(10): 112-116.

HUANGZhengrong，ZHUWei，LIANGJinghua，etal.Astudyonthelimitsupportpressureatexcavationfaceofshieldtunneling[J].ChinaCivilEngineeringJournal， 2006， 39(10): 112-116.

[2] 高健，張義同，喬金麗. 滲透力對隧道開挖面穩(wěn)定性影響分析[J]. 巖土工程學報， 2009， 31(10): 1547-1553.

GAOJian，ZHANGYitong，QIAOJinli.Facestabilityanalysisoftunnelswithconsiderationofseepageforce[J].ChineseJournalofGeotechnicalEngineering， 2009， 31(10): 1547-1553.

[3] 王浩然，黃茂松，呂璽琳，等. 考慮滲流影響的盾構隧道開挖面穩(wěn)定上限分析[J]. 巖土工程學報， 2013， 35(9): 1696-1704.

WANGHaoran，HUANGMaosong，LüXilin，etal.Upper-boundlimitanalysisofstabilityofshieldtunnelfaceconsideringseepage[J].ChineseJournalofGeotechnicalEngineering， 2013， 35(09): 1696-1704.

[4] 鄭永來，馮利坡，鄧樹新，等. 高水壓條件下盾構隧道開挖面極限上限法研究[J]. 同濟大學學報(自然科學版)， 2013， 41(8): 1179-1184.

ZHENGYonglai，F(xiàn)ENGLipo，DENGShuxin，etal.Studyonupper-boundlimitmethodoffacestabilityofshieldtunnelwithhigh-waterpressure[J].JournalofTongjiUniversity(NaturalScience)， 2013， 41(8): 1179-1184.

[5]SalvadorS,RafaelJ.Atunnelfacefailuremechanismforlayeredground,consideringthepossibilityofpartialcollapse[J].TunnellingandUndergroundSpaceTechnology, 2015(47):182-192.

[6]YANGXG,CHISC.Upperboundfiniteelementanalysisofslopestabilityusinganonlinearfailurecriterion[J].ComputersandGeotechnics. 2013(54):185-191.

[7]ZHAOLH,YANGF,ZHANGYB,etal.Effectsofshearstrengthreductionstrategiesonsafetyfactorofhomogeneousslopebasedonageneralnonlinearfailurecriterion[J].ComputersandGeotechnics, 2015(63):215-228.

[8] 張國祥，李麗民，張成平，等. 非線性破壞準則下巖石地基承載力的影響因素[J]. 土木建筑與環(huán)境工程， 2010， 32(5): 16-22.

ZHANGGuoxiang，LILimin，ZHANGChengping，etal.Factorsofbearingcapacityforrockfoundationbasedonthenonlinearfailurecriterion[J].JournalofCivil,Architectural&EnvironmentalEngineering， 2010， 32(5): 16-22.

[9] 趙煉恒，李亮，楊小禮，等. 非線性破壞準則下法向受力條形淺錨抗拔力上限計算方法[J]. 中南大學學報(自然科學版)， 2009， 40(5): 1444-1450.

ZHAOLianheng，LILiang，YANGXiaoli，etal.CalculatingmethodofupperboundforultimatepulloutcapacityofverticallyloadedstripplateanchorsbasedonnonlinearMohr-Coulombfailurecriterion[J].JournalofCentralSouthUniversity(ScienceandTechnology)， 2009， 40(5): 1444-1450.

[10]YANGXL,YINJH.Estimationofseismicpassiveearthpressureswithnonlinearfailurecriterion[J].EngineeringStructures. 2006, 28(3): 342-348.

[11]AgarJG,MorgenstemNR,SeottJ.Shearstrengthandstress-strainbehaviourofAthabascaoilsandatelevatedtemperaturesandpressure[J].CanadianGeotechnicalJournal. 1985, 24(1): 1-10.

[12]ItascaConsultingGroup.FastLagrangiananalysisofcontinuain3dimensions[M].MN,USA:ItascaConsultingGroup,Minneapolis, 2002.

[13] 陳育民，劉漢龍. 鄧肯-張本構模型在FLAC～(3D)中的開發(fā)與實現(xiàn)[J]. 巖土力學， 2007， 28(10): 2123-2126.

CHENYumin，LIUHanlong.DevelopmentandimplementationofDuncan-ChangconstitutivemodelinFLAC3D[J].RockandSoilMechanics， 2007， 28(10): 2123-2126.

[14] 陳育民，徐鼎平.FLAC/FLAC3D基礎與工程實例[M]. 北京: 中國水利水電出版社, 2013: 1-259.

CHENYumin，XUDingping.FLAC/FLAC3Dfoundationandengineeringexample[M].Beijing:ChinaWater&PowerPress, 2013:1-259.

[15] 張箭，楊峰，劉志，等. 淺覆盾構隧道開挖面擠出剛性錐體破壞模式極限分析[J]. 巖土工程學報， 2014， 36(7): 1344-1349.

ZHANGJian，YANGFeng，LIUZhi，etal.Three-dimensionallimitanalysisofblow-outfailuremodesofshallowshieldtunnels[J].ChineseJournalofGeotechnicalEngineering， 2014， 36(7): 1344-1349.

[16] 宋春霞，黃茂松，呂璽琳. 非均質地基中平面應變隧道開挖面穩(wěn)定上限分析[J]. 巖土力學， 2011， 32(09): 2645-2650.

SONGChunxia，HUANGMaosong，LüXilin.Upperboundanalysisofplanestraintunnelinnonhomogeneousclays[J].RockandSoilMechanics， 2011， 32(9): 2645-2650.

[17] 許敬叔，潘秋景. 盾構隧道開挖面支護力上限分析[J]. 鐵道科學與工程學報， 2014， 11(4): 80-84.

XUJingshu，PANQiujing.Upperboundanalysisofsupportingpressureforshieldtunnelfaces[J].JournalofRailwayScienceandEngineering， 2014， 11(4): 80-84.

[18]YANGXL.SeismicdisplacementofrockslopeswithnonlinearHoek-Brownfailurecriterion[J].InternationalJournalofRockMechanicsandMiningSciences. 2007, 44(6): 948-953.

[19] 趙煉恒，羅強，李亮，等. 水平矩形淺錨極限抗拔力分析[J]. 巖土工程學報， 2009， 31(09): 1414-1420.

ZHAOLianheng，LUOQiang，LILiang，etal.Ultimatepulloutcapacityofhorizontalrectangularplateanchors[J].ChineseJournalofGeotechnicalEngineering， 2009， 31(09): 1414-1420.

The study of ultimate support pressure of shield tunnelface subjected to user-defined constitutive model

HUANG Fu1,2, LI Zailan1, ZHU Liang1, YANG Huan1

(1.SchoolofCivilEngineeringandArchitecture,ChangshaUniversityofScience&Technology,Changsha410004,China;2.HunanProvinceResearchCenterforSafetyControlTechnologyandEquipmentofBridgeEngineering,ChangshaUniversityofScience&Technology,Changsha410004,China)

Abstract:To study the influence of nonlinear failure characteristics on the ultimate support pressure of shield tunnel face, the user-defined constitutive model subjected to nonlinear failure criterion was developed by using the further developing platform in FLAC3D. By invoking the constitutive model to simulate the excavation of a shield tunnel, the numerical solution of ultimate support pressure subjected to nonlinear failure criterion was obtained. Furthermore, the nonlinear failure criterion was introduced into the energy calculation by generalized tangential technique, and the upper bound solution of ultimate support pressure for shield tunnel was derived. By comparing the numerical solution and upper bound solution, the validity of ultimate support pressure calculated by user-defined constitutive model was proved.

Key words:ultimate support pressure of tunnel face; nonlinear failure criterion; numerical simulation; upper bound theorem of limit analysis

收稿日期：2015-11-25

基金項目：國家自然科學基金資助項目(51308072,51278071);長沙理工大學橋梁工程安全控制技術與裝備湖南省工程技術研究中心開放基金資助項目(13KC04)；湖南省科技計劃重點項目經(jīng)費資助項目(2014FJ2005)

通訊作者：黃阜(1983-)，男，湖南岳陽人，講師，博士，從事隧道與地下工程的穩(wěn)定性研究；E-mail:hfcsu0001@163.com

中圖分類號：TU921

文獻標志碼：A

文章編號：1672-7029(2016)05-0891-07