外傾式拱梁組合橋梁的穩定性研究

傅金龍，黃天立，夏智

(中南大學 土木工程學院，湖南 長沙 410075)

外傾式拱梁組合橋梁的穩定性研究

傅金龍，黃天立，夏智

(中南大學 土木工程學院，湖南 長沙 410075)

摘要:外傾式拱梁組合橋梁是一種新穎的橋梁形式，然而其外傾式拱肋的穩定性問題十分突出。以一座實橋為背景建立空間有限元模型，并以現有的拱橋穩定性分析理論為指導，對該橋在成橋狀態下和吊桿張拉施工過程中的結構穩定性進行分析，通過對比分析得出：該橋的失穩模態主要表現為拱肋面外失穩；幾何非線性和材料非線性對該橋的穩定性有顯著影響；采用內、外吊桿交替張拉的方式可顯著提高張拉過程中的結構穩定性；外吊桿對該橋的穩定性影響顯著，采用空間多索面體系有利于提高該橋的穩定性。另外，通過大量計算揭示拱肋矢跨比、外傾角及截面剛度等參數對該橋穩定性的影響，并從中得到一些有益的結論，可供同類工程參考。

關鍵詞：外傾式拱肋；穩定性分析；彈性屈曲；非線性；成橋狀態；吊桿張拉過程；參數分析

外傾式拱梁組合橋梁又被稱為蝴蝶拱橋[1]，是一種新穎的橋梁形式，其外觀優美、造型別致，近年來多被用于城市景觀橋梁的建設。該橋型的最為顯著特點就是其外傾式拱肋，即兩片拱肋橫橋向的間距從拱腳處到拱頂處逐漸變大，通常兩片拱肋之間不設置橫向支撐，因而它們之間無法形成整體，然而單片拱肋的側向抗彎剛度和抗扭剛度有限[2]，并且外傾式拱肋本身承受了較大的面外荷載，導致外傾式拱肋的橫向穩定性[3-7]通常較差，容易發生面外失穩，因而有必要對外傾式拱梁組合橋梁的穩定性問題進行研究。本文以江西省南昌市艾溪湖大橋為研究對象，該橋為一座典型的外傾式拱梁組合橋梁，本文首先對該橋在成橋狀態下的空間穩定性進行了分析，而后從吊桿張拉施工過程的結構穩定性的角度考慮，對不同的吊桿張拉方案進行了比選，最后對外傾式拱肋的矢跨比、外傾角以及截面剛度等參數與結構穩定性之間的關系進行了分析，并從中得出了一些有益的結論，可為同類工程的設計與施工提供參考。

1拱橋穩定性分析理論及相關規范要求

拱橋的穩定性問題可以分為2類[8]：第1類穩定問題和第2類穩定問題。第一類穩定問題的力學概念清晰明確，求解相對容易，而且在許多情況下其臨界荷載可近似代表第2類穩定問題的臨界荷載上限。但是，實際的拱橋結構不可避免地存在不同程度的初始彎曲、殘余應力以及偏心等缺陷，因此拱橋在實際工程中的穩定問題通常都表現為第2類穩定問題。實際工程中的拱橋的失穩均發生于彈塑性變形階段，這就需要考慮結構變形和材料彈塑性對結構穩定性的影響，按照幾何非線性和材料非線性來求解拱橋的極限承載力。

1.1有限元分析理論

1.1.1第1類穩定問題的有限元分析理論

在結構發生失穩前，結構滿足線性假設，處于初始構形線性平衡狀態：

([K]0+[K]σ){Δu}={ΔP}

(1)

式中:[K]0為彈性剛度矩陣；[K]σ為幾何剛度矩陣；{Δu}為位移向量；{ΔP}為荷載向量。

當結構處于臨界狀態時，即使{ΔP}→0，{Δu}也應有非零解，因此，可得：

|[K]0+[K]σ|=0

(2)

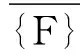
(3)

于是式(2)可寫成：

(4)

式(4)就是第一類穩定問題的控制方程，這樣就將穩定問題轉化為數學上求解特征值的問題。求解方程得到的最小特征值λ即為荷載穩定安全系數，相應的特征向量即為失穩模態[9]。

1.1.2結構極限承載力(第2類穩定問題)有限元分析理論

從力學分析角度看，分析橋梁結構極限承載力的實質就是通過不斷計入幾何非線性和材料非線性對剛度矩陣的影響，求解平衡方程，尋找其極限荷載的過程。結構在不斷增加的外荷載作用下，剛度不斷發生變化，當外荷載產生的壓應力或剪應力使得結構切線剛度矩陣趨于奇異時，結構承載能力就達到了極限，此時的外荷載即為極限荷載[9]。

全過程分析通過逐級增加工作荷載集度來考察結構的變形和受力特征，一直計算至結構發生破壞。通常采用荷載增量法來求解出結構在承受荷載全過程中的荷載—位移(P-Δ)曲線，從而確定結構的極限荷載。整個結構的增量方程為：

(0[K]0+0[K]σ+0[K]L){Δu}i={ΔP}i

(5)

式中:0[K]0，0[K]σ和0[K]L分別為t=0時刻的結構的彈性剛度矩陣、幾何剛度矩陣和初位移剛度矩陣，{Δu}i為第i次加載 {ΔP}i時產生的節點位移增量。

1.2現行規范對拱橋結構穩定的要求

現行規范通常要求拱橋的彈性特征值安全系數不小于4，而對于非線性穩定安全系數并沒有非常明確的規定。規范[10]要求對鋼管混凝土拱橋進行空間穩定性分析，且其彈性特征值安全系數不應小于4.0；對于特大跨徑的鋼管混凝土拱，由于其材料非線性或幾何大變形或雙重非線性對結構整體穩定影響較大，一般還應進行考慮非線形的極值點穩定計算。規范[11]與規范[10]關于彈性特征值穩定安全系數的規定基本相同，但規范[11]同時還對非線形整體穩定安全系數提出參考安全值，一般要求其不小于2.0。規范[12]要求對拱肋(拱圈)平面內的穩定性進行檢驗，按照其承受最大水平推力的中心受壓桿件進行檢算，其穩定安全系數不得小于4～5，必要時還應檢算拱肋平面外的穩定性。另外，文獻[13]指出，對于跨徑大于200m的鋼管混凝土拱橋，其整體彈性穩定系數不小于4.0；其穩定極限承載能力要考慮材料的非線性和幾何非線性的影響，極限承載能力與設計荷載之比不宜小于2.0。

實際工程中的橋梁結構失穩多屬于第二類穩定問題，但無論是第一類失穩還是第二類失穩，對于相同受力狀態下的同一結構，兩類失穩對應的可靠指標應是一致的，且應保證結構可靠指標不小于目標可靠指標[14]。另外，文獻[14]還指出，第1類穩定安全系數取4時，并不能保證結構實際發生的第2類失穩的可靠指標達到目標可靠指標，因此，若采用第一類失穩模式進行結構穩定性驗算，相應的穩定安全系數的取值應重新審視。

2工程實例

本文以艾溪湖大橋為工程實例，該橋為一座三跨連續外傾式拱梁組合橋梁，全長168m，中間主跨的跨徑為108m，兩邊跨的跨徑均為30m。主跨的車行道全寬為31m，兩側非機動車道道寬由端部的5m按曲線漸變至跨中的7.5m。圖1和圖2分別為艾溪湖大橋的平面圖和立面圖。

該橋的主梁為鋼箱結構，分為主跨和副跨兩部分，即機動車道的鋼箱梁為主跨，兩側非機動車道的鋼箱梁為副跨。鋼箱拱肋由主拱和裝飾拱組成，兩者的拱軸線均為拋物線，裝飾拱不參與結構受力；主拱的橫截面為變截面，截面尺寸由拱腳處的2.5m×2m(寬×高)漸變至拱頂處的1.5m×1.3m；拱肋平面向外傾斜，斜度為3:1，兩片傾斜拱肋之間不設置橫向支撐。吊桿分為內吊桿和外吊桿兩種類型，內、外吊桿的縱向間距均為4m；內吊桿共計25對，與車行道鋼箱梁上的吊點相連，參與承擔恒載及車行活載；外吊桿共計21對，與人行道鋼箱梁上的吊點相連，參與承擔恒載及人行活載；需要指出的是，該橋的內吊桿和外吊桿均與拱肋平面成一定夾角。系桿布置在車行鋼箱主梁內部，用于平衡拱肋拱腳處的水平推力，共計4組系桿，每片拱肋兩組。

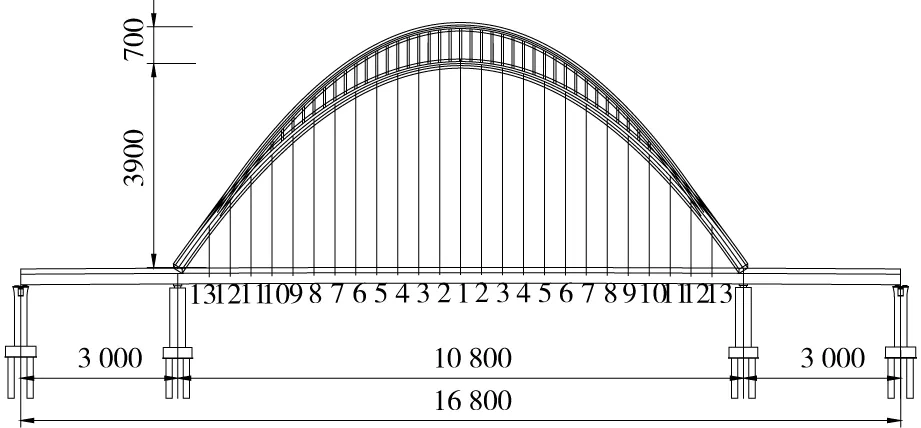
單位：cm圖1　艾溪湖大橋立面圖Fig.1 Elevation of Aixi Lake bridge

單位：cm圖2　艾溪湖大橋平面圖Fig.2 Plan of Aixi Lake bridge

3橋梁結構穩定性分析

本文應用有限元分析軟件ANSYS建立了艾溪湖大橋的空間有限元模型，其鋼箱拱肋采用梁單元Beam188進行模擬，該類型單元可考慮大轉角、大應變及剪切效應等因素的影響，適宜進行非線性分析[15]；由于鋼箱主梁的寬度較大，故將其分成8片分梁，采用梁格法建模，各分梁均采用梁單元Beam188進行模擬；主梁橫隔板采用集中質量單元Mass21進行模擬，并計入其質量和質量慣性矩；吊桿和系桿均采用link10單元進行模擬，當出現壓應力時，剛度為零，可較好地模擬柔性索的力學性能。

3.1成橋狀態時的結構穩定性分析

3.1.1第一類穩定分析

通過有限元分析計算，得到了艾溪湖大橋成橋狀態時在6種荷載工況作用下的彈性特征值穩定安全系數，如表1所示。該6種荷載工況作用下的全橋一階屈曲模態均為拱肋單波面外失穩，圖3為工況荷載1作用下的前三階屈曲模態，可供參考。另外，本文按照基本風速為27.2m/s來計算風荷載，僅考慮主梁和拱肋所受靜風荷載中的迎風阻力，忽略了升力和扭矩的影響，相關計算可參考規范[16]。

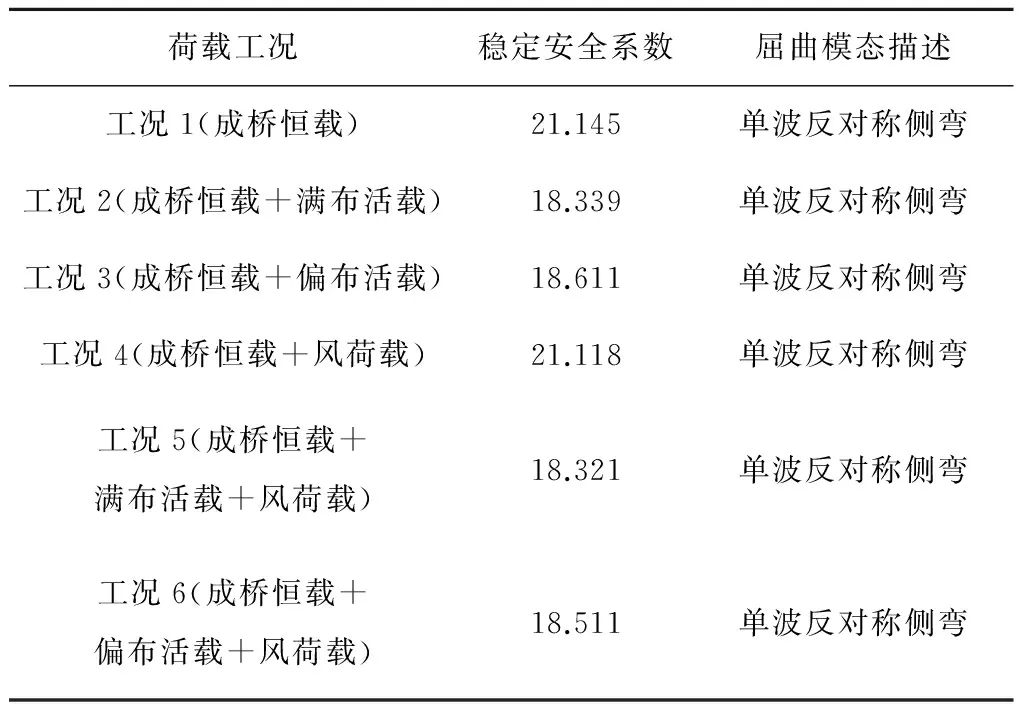
表1　彈性特征值穩定安全系數

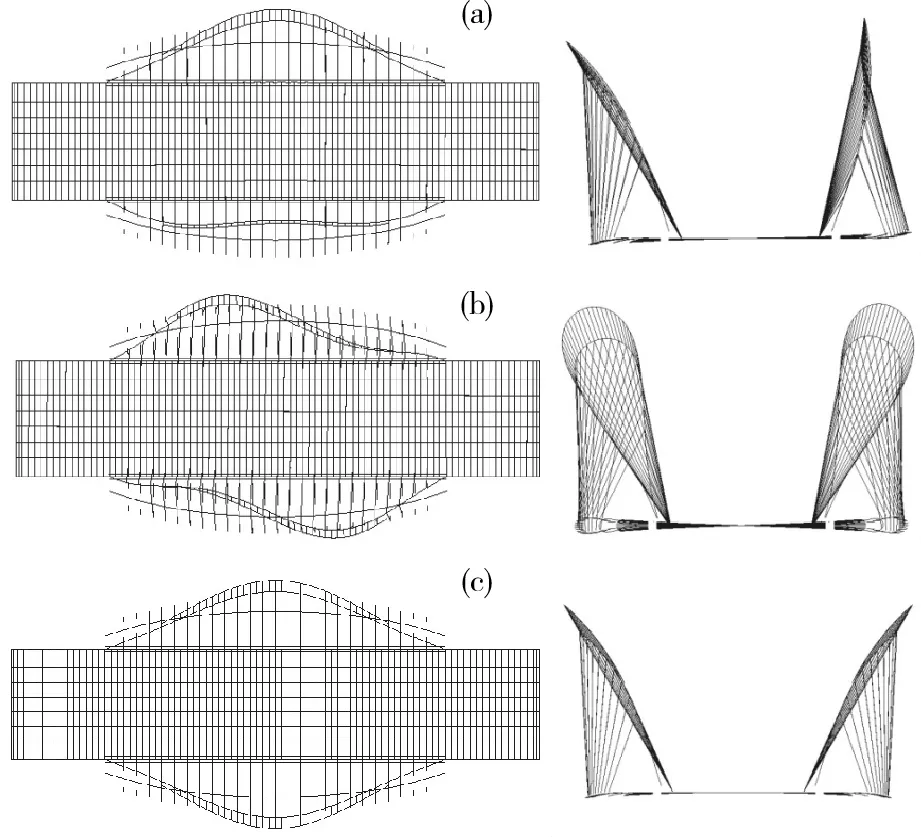
(a)一階失穩模態；(b)二階失穩模態；(c)三階失穩模態圖3　工況荷載1作用下的全橋屈曲模態Fig.3 Bridge buckling modes under load condition 1

由表1中的計算結果可以看出，以上6種荷載工況作用下的成橋穩定安全系數均在18以上，滿足通常拱橋第一類穩定安全系數不小于4～5的要求；在成橋恒載的基礎上再考慮風荷載的作用時，橋梁的穩定安全系數變化不大，可見風荷載對本橋的第一類穩定計算結果影響不大；在成橋恒載的基礎上再考慮活載的作用時，該橋的穩定安全系數明顯降低，表1中荷載工況2對應的安全穩定系數比荷載工況1降低了13.3%，表明活載對橋梁結構的穩定性影響較大。

3.1.2第二類穩定分析

第1類穩定理論建立在理想的線彈性、小位移理論基礎之上，雖然其理論清晰，計算方便，但其計算得到的臨界荷載值通常高于結構失穩的實際臨界荷載值。而第2類穩定分析理論建立在結構非線性、大位移理論基礎之上，它考慮了結構變形和材料彈塑性對結構穩定性的影響[9,17]。本文利用第3類穩定分析理論，分別考慮了幾何非線性因素和材料非線性因素的影響，對艾溪湖大橋的進行了極限承載力分析。

采用非線性有限元理論對艾溪湖大橋主橋進行幾何非線性分析，只考慮拱橋恒載作用，得到了拱頂處面外位移的P-Δ曲線，如圖4中曲線a所示，圖中λ為荷載系數，它是所施加的荷載與設計荷載之間的比值，其最大值即為穩定安全系數K。

由P-Δ曲線(曲線a)可以看出，曲線起始段的荷載(系數)與位移之間呈線性關系，隨著荷載的不斷增加，非線性關系逐漸顯現，在接近極限荷載時，位移迅速增加，曲線基本呈水平狀。考慮幾何非線性后的穩定安全系數為17.911，而彈性特征值穩定安全系數為21.145，相比下降了15.3%，由此可知，對于本文算例而言，幾何非線性因素對結構穩定性計算具有重要影響。

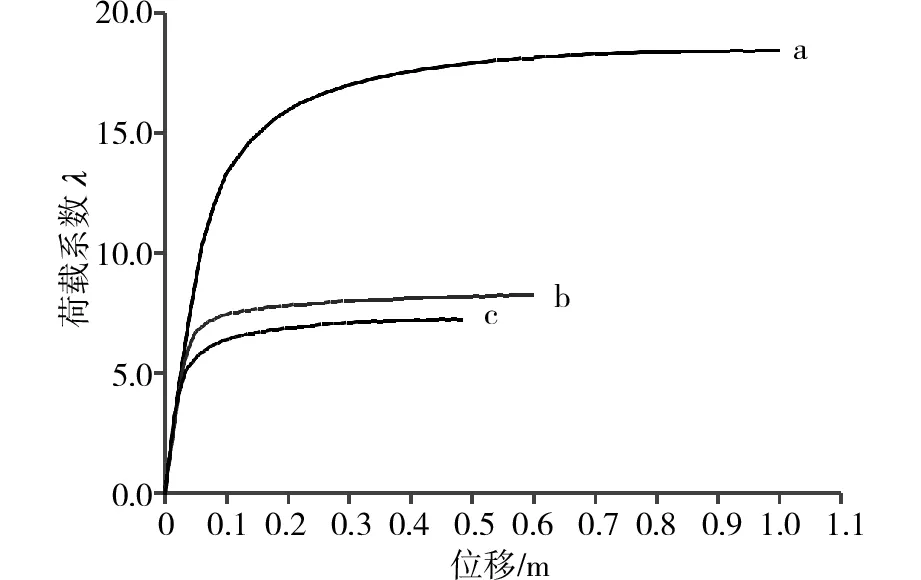
圖4　荷載—位移曲線(P-Δ曲線)Fig.4 Load-displacement curves (P-Δcurves)

由于艾溪湖大橋的前三階屈曲模態均為拱肋面外失穩，因而在進行材料非線性分析時，只需考慮鋼箱拱肋的材料非線性。考慮材料非線性因素對結構穩定性的影響，其主要問題就是材料本構關系的選取。鋼箱拱肋采用Q345D鋼材，其屈服強度fy=345MPa，本文采用雙線性理想彈-塑性模型來模擬鋼材的本構關系[2]，其應力-應變關系為：

(6)

式中：fy為鋼材屈服應力；εy為鋼材屈服時對應的應變。

利用上述拱肋鋼材的本構關系模型，對艾溪湖大橋進行材料非線性分析，只考慮拱橋恒載作用，得到拱頂處面外位移的P-Δ曲線，如圖4中的曲線b所示。考慮材料非線性后的穩定安全系數為8.041，相比彈性特征值穩定安全系數下降了62%，由此可知，對于本文算例，材料非線性因素的對結構穩定性分析結果影響巨大，比幾何非線性因素更為顯著，不可忽略。

通過以上分析得知，幾何非線性因素和材料非線性因素對結構穩定的分析結果均有重要影響，因此在對結構穩定性進行分析時，應同時考慮雙重非線性的影響。對艾溪湖大橋進行雙重非線性分析，只考慮拱橋恒載作用，得到拱頂處面外位移的P-Δ曲線，如圖4中曲線c所示。考慮雙重非線性后的穩定安全系數為7.265，相比彈性特征值穩定安全系數下降了65.6%，由此可知，一定要同時考慮材料非線性因素和幾何非線性因素的影響，才能得到較為可靠的穩定分析結果。

3.2吊桿張拉施工過程中的結構穩定性分析

對于吊桿張拉施工而言，選擇合理的張拉方案至關重要，合理的吊桿張拉方案應使張拉過程結構所經歷的一切中間狀態均滿足結構的內力、變形及機具承載力的要求，并最終達到預先要求的目標設計狀態，簡而言之，它是一條達到指定目標狀態的合理(最優)路徑。但是，僅考慮吊桿張拉過程中結構的受力和變形是不夠的，結構穩定性也應充分考慮，尤其是拱肋的穩定性。對于橋梁工程而言，結構的最不安全狀態不一定出現在成橋運營階段，相反起控制作用的結構狀態往往出現在施工階段，而且很多情況下，結構在施工過程中的穩定性要低于成橋的穩定性，因此，有必要對艾溪湖大橋在吊桿張拉施工過程中的結構穩定性進行分析[18]。

本文假定艾溪湖大橋可在不設置拱肋間臨時橫撐或支架支護的情況下進行吊桿張拉施工，并選取了3種不同的吊桿張拉方案進行對比分析，此3種吊桿張拉方案分別是：

1)張拉方案1：由拱頂區至拱腳區依次對稱張拉吊桿；2)張拉方案2：由拱腳區至拱頂區依次對稱張拉吊桿；3)張拉方案3：由四分區開始交替對稱張拉吊桿。

此3種吊桿張拉方案均采用先張拉內吊桿，而后張拉外吊桿的模式，共需張拉24組次吊桿。此3種張拉方案對應的具體的吊桿張拉順序和吊桿施工張拉力分別下表2所示，吊桿編號見上圖1，另外，表2中的“N”表示內吊桿，“W”表示外吊桿。

通過有限元建模來模擬吊桿張拉過程，并計算得到了每一組次吊桿張拉完成后的結構穩定安全系數，如圖5和表3所示。圖5和表3中的“0吊桿張拉組次”表示吊桿張拉前的結構狀態，即裸拱狀態，作為吊桿張拉的起點，3種張拉方案在裸拱狀態下的穩定安全系數同為27.624。

由圖5可見，吊桿張拉方案1，方案2和方案3對應的結構穩定安全系數變化曲線的前半段均呈單調遞減趨勢，表明隨著內吊桿的張拉，結構的穩定性逐漸變差，并在內吊桿張拉完畢時(對應吊桿張拉組次13)結構穩定安全系數達到最小值；3種吊桿張拉方案對應的結構穩定安全系數變化曲線的后半段均為單調遞增趨勢，表明隨著外吊桿的張拉，結構的穩定性逐漸變好，并在外吊桿張拉完畢時(對應吊桿張拉組次24)結構穩定安全系數達到最大值。由此可知，雖然外吊桿的索力值相對較小(不及內吊桿的索力值的0.1倍)，但由于其與拱面之間的夾角較大，張拉外吊桿后的結構穩定安全系數顯著提高，可見，對于外傾式拱梁組合橋梁而言，外吊桿必不可少，因而發展成為空間多索面體系也成為必然。

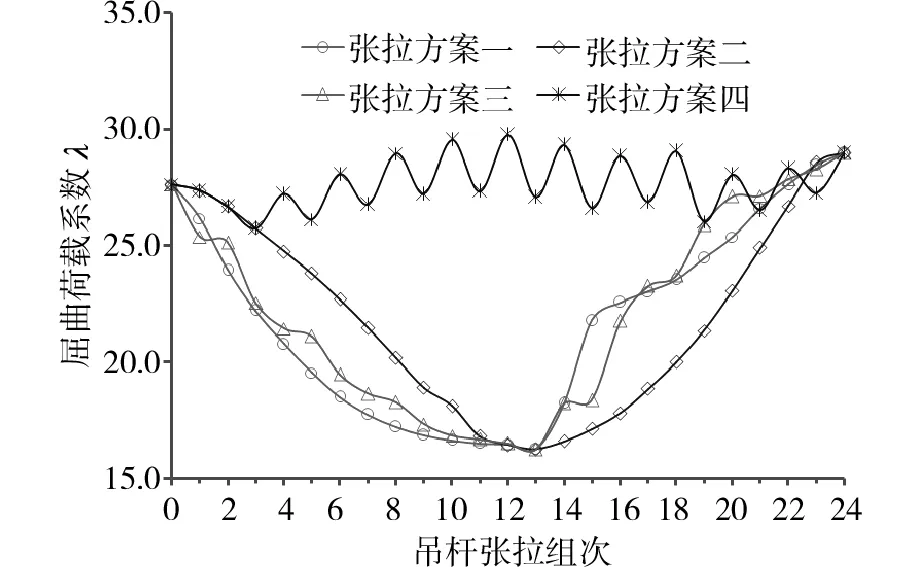
圖5　吊桿張拉過程中的結構穩定安全系數變化曲線Fig.5 Curves of stability safety coefficients during the suspenders tensioning processes

認真觀察圖5還可發現，張拉方案一對應的穩定安全系數變化曲線隨著內吊桿的張拉先快速下降，但下降速度逐漸變慢，而后隨著外吊桿的張拉快速上升，但上升速度逐漸減慢，結合張拉方案一對應的吊桿張拉順序可知：吊桿越靠近跨中，張拉該組次吊桿對結構的穩定性影響就越大。張拉方案二對應的穩定安全系數變化曲線隨著內吊桿的張拉先慢速下降，但下降速度逐漸加快，而后隨著外吊桿的張拉先慢速上升，但上升速度逐漸加快，這種現象同樣支持上述觀點。張拉方案三對應的穩定安全系數變化曲線大致上呈階梯狀，曲線中的快速下降段和快速上升段都對應于拱頂區的吊桿張拉，這種現象依然支持上述觀點。

基于以上分析可知，不同的吊桿張拉方案對吊桿張拉施工過程中的結構穩定性有相當程度的影響，張拉方案1、方案2和方案3均采用“先將內吊桿張拉完畢，再進行外吊桿張拉”的模式，導致內吊桿張拉完畢時結構的穩定安全系數降至最低。 本文嘗試采用“將內吊桿和外吊桿相互交替張拉”的模式，其具體的吊桿張拉順序和吊桿施工張拉力如上表2中的張拉方案4所示。張拉方案4對應的張拉過程中的結構穩定系數可見于上表3和圖5，在吊桿張拉過程中，結構的穩定安全系數并沒有呈現單調遞減或遞增的現象，而是在27.5附近上下波動，其穩定安全系數的最小值為25.74(對應于吊桿張拉組次3)，比前3種吊桿張拉方案對應的穩定安全系數最小值提高了58.6%，使得吊桿張拉施工過程中結構穩定性顯著提高。因此從結構穩定性的角度考慮，吊桿張拉方案4優于張拉方案1、方案2和方案3。

表3吊桿張拉過程中的結構穩定安全系數

Table3Stabilitysafetycoefficientsduringthesuspenderstensioningprocesses

吊桿張拉組次穩定安全系數張拉方案1張拉方案2張拉方案3張拉方案4027.62427.62427.62427.624126.16127.34725.36827.347223.93626.66825.11726.668322.19725.74022.53525.740420.75024.74321.42527.219519.52023.78521.08626.118618.47422.68119.44528.051717.72821.46018.61926.750817.19520.15118.25228.956916.82518.87417.2927.2121016.61618.08716.82129.5531116.47916.79516.65527.3271216.40516.40916.47729.7651316.23116.22516.22827.0711418.20516.56918.19829.3201521.76317.10418.35326.5981622.55517.78821.74728.8491723.01118.82423.26326.8581823.51219.96923.69929.0621924.45921.33525.88126.0312025.36023.04927.11928.0352126.60424.89627.13626.5102227.62326.69327.84628.3172328.45528.56428.28327.2722428.98228.97828.98428.976

以上4種吊桿張拉方案對應的張拉過程中的所有結構暫態的彈性特征值穩定安全系數均滿足相關規范不小于4～5的要求，單從此第一類穩定分析的結果考慮，可認為在以上4種吊桿張拉方案對應的張拉過程中的外傾式拱肋穩定性是滿足要求的。為安全起見，本文還對吊桿張拉過程的各結構暫態進行了第2類穩定分析，圖6為張拉方案1、方案2和方案3對應的第13組次吊桿張拉完畢(即僅內吊桿張拉完畢)時的結構暫態的雙重非線性分析結果，其穩定安全系數為5.625，而且其他各結構暫態的第2類穩定安全系數也均滿足相關規范不小于2的要求。由此可知，本文考慮的4種張拉方案均滿足結構穩定性要求，但以方案4為最優；同時也證明了本橋算例在吊桿張拉過程中無需設置拱肋間的臨時橫撐或支架等張拉輔助設施。

圖6　雙重非線性分析得到的P-Δ曲線(K=5.625)Fig.6 P-Δcurve of double nonlinear analysis results (K=5.625)

4穩定性影響因素的參數分析

4.1拱肋矢跨比的影響

對于外傾式拱梁組合體系而言，拱肋的矢跨比是一個重要的參數[19]，矢跨比對橋梁的穩定性具有重要影響。保持艾溪湖大橋拱肋的外傾角和跨度不變，通過改變拱肋矢高來改變矢跨比，計算得到恒載作用下拱肋矢跨比與穩定安全系數之間的關系曲線，如圖7所示。

由圖7中的曲線可知，存在最優的矢跨比使得橋梁的穩定安全系數達到極大值，該最優矢跨比介于0.20和0.25之間。當拱肋矢跨比較小時，隨著矢跨比的增大，特定荷載作用下的拱肋軸向壓應力將顯著減小，故而穩定安全系數也隨之增大；而當拱肋矢跨比較大時，隨著矢跨比的增大，拱肋軸向壓應力減小不明顯，計算長度反而隨之顯著增大，故而穩定安全系數隨之減小。然而，艾溪湖大橋采用的拱肋矢跨比為0.381，顯然偏離最優矢跨比較多，從結構穩定安全的角度考慮這并不合理。基于橋梁美學方面的原因，艾溪湖大橋通過采用較大的矢跨比來突出外傾式拱肋的別致造型，但同時這也提高了橋梁的整體造價，造成了景觀與效益之間的矛盾。

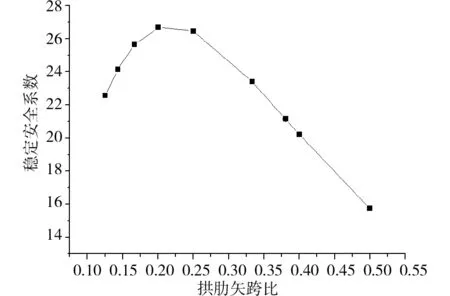
圖7　拱肋矢跨比與穩定安全系數之間的關系Fig.7 Relationship between ratios of height and span and stability safety coefficients

4.2拱肋外傾角的影響

由前文已知，艾溪湖大橋的失穩模態主要是拱肋面外失穩，而拱肋外傾角是引起拱肋承受面外荷載的主要原因之一，因而其對拱肋穩定性有重要影響[20]。保持艾溪湖大橋拱肋的矢高和跨度不變，僅改變其拱肋外傾角度，計算得到了恒載作用下拱肋外傾角度與橋梁穩定安全系數之間的關系曲線，如下圖8所示。

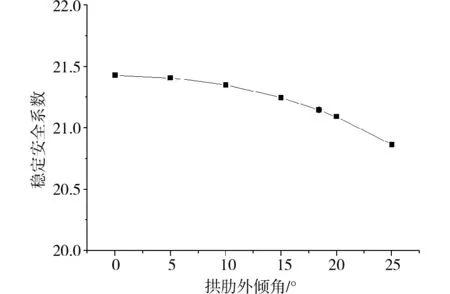
圖8　拱肋外傾角與穩定安全系數之間的關系Fig.8 Relationship between camber angles of arch rib and stability safety coefficients

由圖8中的曲線可知，隨著拱肋外傾角的不斷增大，橋梁的穩定安全系數隨之下降，而且下降速度不斷加快。由此可知，拱肋的外傾角對其穩定性并無積極影響，該橋之所以設置18.435。的外傾角度，完全是基于橋梁美學方面的原因。

4.3拱肋剛度的影響

對于外傾式拱梁組合橋梁而言，為了達到其美學效果，拱肋的矢跨比和傾角通常難以進行過多的優化，因而只能從拱肋的截面特性著手來改善結構的穩定性[19]。本文通過改變艾溪湖大橋拱肋的剛度，計算得到了恒載作用下拱肋剛度與橋梁穩定安全系數之間的關系曲線，如下圖9所示。

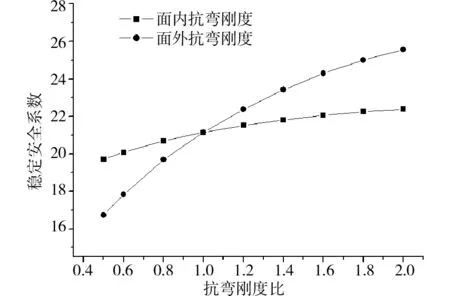
圖9　拱肋剛度與穩定安全系數之間的關系Fig.9 Relationship between section rigidities of arch rib and stability safety coefficients

由圖9中的曲線可知，隨著拱肋面內抗彎剛度的增大，穩定安全系數隨之增大，但增幅并不明顯，當拱肋面內剛度增大至原來的2倍時，橋梁的穩定安全系數僅僅增大了5.9%；隨著拱肋面外抗彎剛度的增大，穩定安全系數也隨之增大，且增幅較為明顯，當拱肋面內剛度增大至原來的2倍時，橋梁的穩定安全系數增大了20.1%。由此可知，可通過增加拱肋面外抗彎剛度的方法來改善結構穩定性，但隨著拱肋面外抗彎剛度的增大，其對穩定性的影響越來越不明顯。

5結論

1)艾溪湖大橋的彈性特征值穩定安全系數滿足通常規范不小于4～5的要求，由于其外傾式拱肋承受了較大的面外荷載且橋面系的剛度較大，橋梁的失穩模態主要表現為拱肋面外失穩。

2)對于外傾式拱梁組合橋梁而言，空間多索面形式是使外傾式拱肋穩定的有力保障，艾溪湖大橋的拱肋在內、外吊桿的共同作用下，其穩定性顯著提高。

3)在吊桿張拉施工過程中，選擇不同的吊桿張拉方案對張拉施工過程中結構穩定性有較大影響，艾溪湖大橋的外吊桿對結構穩定性影響較大，采用內吊桿和外吊桿相互交替張拉的吊桿張拉方案可顯著提高張拉施工過程中的結構穩定性。

4)由于橋梁美學方面的原因，艾溪湖大橋的拱肋采用了外傾形式和較大的矢跨比，但是這些對其結構的穩定性均產生了不利影響，可通過提高拱肋剛度的方式，尤其是拱肋面外抗彎剛度，來改善其結構穩定性。

參考文獻：

[1] 易云焜. 梁拱組合體系設計理論關鍵問題研究[D]. 上海：同濟大學, 2007.

YIYunkun.Key-problemstudyfordesigntheoryofbeam-archassociationbridges[D].Shanghai:TongjiUniversity, 2007.

[2] 譚紅霞,陳政清,封周權. 剛構-單拱肋組合橋梁的穩定性研究[J]. 振動與沖擊, 2008,27(12):122-125.

TANHongxia,CHENZhengqing,FENGZhouquan.Stabilityofcombinativebridgewithrigidframeandsingle-ribbedarch[J].JournalofVibrationandShock, 2008, 27(12):122-125.

[3]RenWeixin,ZhaoTong,IssamE.Analysisofsteelarchbridge[J].JournalofStructureEngineering, 2004,130(1):1022-1031.

[4]DouC,GouYL,ZhaoSY.Elasticout-of-planebuckingloadsofcircularsteeltubulartrussarchesincorporatingshearingeffects[J].EngineeringStructure, 2013, 52:697-706.

[5] 季日臣,石明星. 大跨度鐵路鋼管混凝土系桿拱橋穩定性分析[J]. 振動與沖擊, 2011,30(8):87-91.

JIRichen,SHIMingxing.StabilityanalysisoflongspanrailwayCESTtied-archbridge[J].JournalofVibrationandShock, 2011, 30(8):87-91.

[6] 陳淮,楊磊. 湛河提籃式拱橋空間彈性穩定性分析[J]. 鐵道科學與工程學報, 2013,10(2):1-4.

CHENHuai,YANGLei.SpatialelasticstabilityanalysisoftheZhanheX-stylearchbridge[J].JournalofRailwayScienceandEngineering, 2013, 10(2):1-4.

[7] 王艷,陳淮. 大跨徑鋼管混凝土桁架拱橋穩定性分析[J]. 鐵道科學與工程學報, 2010,7(1):7-10.

WANGYan,CHENHuai.Stabilityanalysisoflongspanconcretefiledsteeltubulartrussarchbridge[J].JournalofRailwayScienceandEngineering, 2010, 7(1):7-10.

[8] 李國豪. 橋梁結構穩定與振動[M]. 北京：中國鐵道出版社, 2003.

LIGuohao.Stabilityandvibrationofbridgestructure[M].Beijing:RailwayPublishingHouseofChina, 2003.

[9] 項海帆. 高等橋梁結構理論[M]. 北京：人民交通出版社, 2013.

XIANGHaifan.Advancedtheoryofbridgestructure[M].Beijing:ChinaCommunicationPress, 2013.

[10]GB50923—2013,鋼管混凝土拱橋技術規范[S].

GB50923—2013,Technicalspecificationforconcretefilledsteeltubulararchbridge[S].

[11]CQJTG/TD66—2011,公路鋼管混凝土拱橋設計規范[S].

CQJTG/TD66—2011,Designspecificationforhighwayconcretefilledsteeltubulararchbridge[S].

[12]TB10002.1—2005,鐵路橋涵設計基本規范[S].

TB10002.1—2005,Basicspecificationfordesignofrailwaybridgeandculvert[S].

[13] 牟廷敏,莊衛林,梁健,等. 公路鋼管混凝土橋梁設計與施工指南[M].北京：人民交通出版社,2008.

MOUTingmin,ZHUANGWeilin,LIANGJian,etal.Guidefordesignandconstructionofhighwayconcretefilledsteeltubulararchbridge[M].Beijing:ChinaCommunicationPress, 2008.

[14] 童小龍,方志. 基于可靠度指標的橋梁結構穩定安全系數研究[J]. 鐵道學報, 2014,36(10):102-108.

TONGXiaolong,FANGZhi.Studyonstabilitysafetyfactorofbridgestructurebaseduponreliabilityindex[J].JournaloftheChinaRailwaySociety,2014,36(10): 102- 108.

[15] 王元清,姜波,石永久. 大跨度鋼管混凝土拱橋施工穩定性分析[J]. 鐵道科學與工程學報, 2006, 3(5):1-5.

WANGYuanqing,JIANGBo,SHIYongjiu.Analysisofstabilityoflong-spanconcretefilledsteeltubearchedbridgeinconstruction[J].JournalofRailwayScienceandEngineering, 2006,3(5):1-5.

[16]JTGD60—2004,公路橋涵設計通用規范[S].

JTGD60—2004,Generalspecificationfordesignofhighwaybridgesandculverts[S].

[17] 崔軍,王景波,孫炳楠. 大跨度鋼管混凝土拱橋非線性穩定分析[J]. 哈爾濱工業大學學報,2003,35(7):876 -878.

CUIJun,WANGJingbo,SUNBingnan.Nonlinearbuckinganalysisforlargespanconcretefilledsteeltubearchbridge[J].JournalofHarbinInstituteofTechnology, 2003,35(7):876-878.

[18] 應明,鄭一峰,王德軍. 吊桿張拉過程中的拱肋穩定性分析[J]. 哈爾濱工業大學學報, 2011,43(4) :142- 144.

YINGMing,ZHENGYifeng,WANGDejun.Stabilityanalysisofarchribintheprocessofdrawingboom[J].JournalofHarbinInstituteofTechnology, 2011,43(4):142-144.

[19] 李雅香. 城市非對稱外傾拱肋鋼拱橋受力特性研究[D]. 成都：西南交通大學,2011.

LIYaxiang.Amechanicalcharacteristicsstudyonurbansteelarchbridgeswiththeasymmetrictiltarch[D].Chengdu:SouthwestJiaotongUniversity, 2011.

[20] 陳淮,孫應桃. 斜靠式拱橋拱肋傾角變化對穩定性能的影響[J]. 鐵道科學與工程學報, 2009,6(1) :21- 24.

CHENHuai,SUNYingtao.VariationalslopingangleofarchribinfluencedonthestabilityofdoubleX-shapedarchbridge[J].JournalofRailwayScienceandEngineering, 2009,6(1):21-24.

Stability analysis of external slanted arch-beam combination bridges

FU Jinlong,HUANG Tianli,XIA Zhi

(School of Civil Engineering, Central South University, Changsha 410075, China)

Abstract:The external slanted arch-beam combination bridge is a new type of bridge, and the stability problem of its external slanted arch is significant. This paper took the Aixi Lake Bridge located in Nanchang city as the real-world engineering project and established the spatial finite element model of the bridge accordingly. In combination with the existing stability analysis theories for arch bridges, the stability of the Aixi Lake Bridge was analyzed with the process of suspenders tension and the completed bridge state taken into account. The analysis results indicate that the bucking mode of the bridge is mainly shown by out-plane bucking of the arch rib, and that the influence of geometrical nonlinearity and material nonlinearity on the stability of the bridge is significant. Adopting the pattern of tensioning inner-suspenders and outer-suspenders sequentially can improve the stability level of the bridge during the process of suspender tension. The outer-suspenders have positive impacts on the stability of the bridge; therefore, adopting the form of spatial multi suspenders system can improve the stability level significantly. Furthermore, through a number of calculations and analyses, the effects of geometrical parameters of arch rib, such as the ratio of height to span, camber angle and section rigidity, on the stability of the bridge are revealed with several insightful conclusions drawn. The findings in this paper can provide useful reference and guidance for similar projects.

Key words：external slanted arch rib; stability analysis; elastic buckling; nonlinearity; completed bridge state; suspenders tensioning process; parameters analysis

收稿日期：2015-11-29

基金項目：國家自然科學基金資助項目(51478472);湖南省自然科學基金資助項目(2015JJ2176);英國牛頓基金資助項目(Reference NRCP/1415/14)

通訊作者：黃天立(1977-)，男，湖南長沙人，副教授，博士，從事橋梁工程研究；E-mail: htianli@csu.edu.cn

中圖分類號：U448.22

文獻標志碼：A

文章編號：1672-7029(2016)05-0853-10