基于GM(1,1)冪模型的凍脹區高速鐵路軌面不平順發展預測

郭毅，高建敏

(西南交通大學 牽引動力國家重點實驗室,四川 成都 610031)

基于GM(1,1)冪模型的凍脹區高速鐵路軌面不平順發展預測

郭毅，高建敏

(西南交通大學 牽引動力國家重點實驗室,四川 成都 610031)

摘要:根據凍脹區高速鐵路軌面不平順的發展特征，應用灰色系統理論，建立以凍脹區高速鐵路軌面不平順檢測數據為時間序列的非等時距GM(1,1)冪模型，優化模型的初始值和背景值以提高預測精度；利用粒子群智能算法求解冪指數，并采用諧波變換生成的周期性函數與正弦函數相結合的方法對殘差進行組合修正，以更好地擬合不平順發展中的隨機性成分。在此基礎上，應用所建立的模型對某凍脹區高速鐵路軌面不平順在路基凍脹發育過程中的發展進行擬合預測。研究結果表明：所建立的模型能夠較好地反應凍脹區高速鐵路軌面不平順在路基凍脹發生期間隨時間的隨機變化過程，模型能夠利用40 d左右的不平順數據較為準確的預測未來10～20 d不平順變化情況，擬合值的平均相對誤差為約5.64%，預測值的平均相對誤差為約6.47%。研究結果可為凍脹區高速鐵路軌面不平順的養護維修提供參考。

關鍵詞：高速鐵路；軌面不平順；路基凍脹；GM(1,1)冪模型；發展預測

我國季節性凍土區約占國土面積的55%，已建、在建和擬建的高速鐵路與快速客運專線三分之一以上均位于深季節凍土地區[1-2]。寒區高速鐵路路基凍脹是困擾高速鐵路建設和運營的關鍵技術難題之一。路基凍脹具有普遍性、不確定性和難以避免等特點，將嚴重破壞軌面的整體平順狀態[3]。軌面幾何不平順作為輪軌系統的激擾源，是引起機車車輛產生振動和輪軌動作用力的主要原因[4]，當高速車輛通過凍脹區域時，由于路基凍脹變形引起的軌面幾何狀態的變化一方面將造成較大的輪軌附加動荷載，導致車輛運行品質下降，對行車安全性和舒適性產生威脅；另一方面，由于軌下基礎的凍脹變形，造成鋼軌和軌下基礎受力狀態變化，進而導致鋼軌和軌下基礎變形和傷損加劇，反過來又會惡化軌面幾何狀態，加劇輪軌相互作用，如此形成惡性循環，嚴重影響高速鐵路線路的服役狀態與使用壽命。針對季節性凍土地區的路基凍脹問題，目前己經釆取了多種防凍脹措施，但在實際運營中依然存在一定的凍脹變形，破壞了軌面的平順狀態，影響高速行車的動力性能。根據哈大高速鐵路2012年全線凍脹觀測數據，全線凍脹變形量大于零的測點數占總測點數的75.7%，凍脹量大于5 mm的測點數占總測點數的19.5%[3]。吉琿客運專線在2013-2014年監測到的數據顯示，路基凍脹量大于零的測點占總監測點的80.12%，大于12 mm的監測點占全部監測點數的6.01%[5]。目前大量的研究工作圍繞路基凍脹產生的原因、變化規律及其防治等開展，對于由于路基凍脹而引起的軌面不平順變化規律及其動力影響的研究較少。基于上述背景，有必要結合實際情況，開展高速鐵路路基凍脹引起的軌面不平順特征及其變化規律的研究，掌握凍脹區高速鐵路軌面幾何不平順的特點及其發展變化規律，進而建立合理的線路狀態預測模型，分析與預測凍脹區高速鐵路軌面幾何狀態變化的未來趨勢與形態，以期為凍脹區高速鐵路軌道養護維修計劃的制訂提供參考。在基于實測數據預測模型研究方面，鄧聚龍在1982年創立的灰色系統理論，以部分信息已知、部分信息未知的小樣本、貧信息不確定性系統為研究對象，通過對部分已知信息的生成、開發，提取有價值點的信息，實現對系統運行行為、演化規律的正確描述和有效監控[6]。目前在鐵路行業，灰色系統理論已經用于軌道質量預測、路基沉降變形預測等領域，曲建軍等[7-8]基于灰色GM(1,1)模型，建立了非等時距的修正模型和軌道幾何狀態中長期時變參數預測模型，進行了軌道質量的預測；張玉芝等[9]利用灰色GM(1,1)模型建立了動態灰色新陳代謝預測模型群，并將其用于高速鐵路路基沉降變形的實時預測；郭然等[10]利用灰色GM(1,1)模型建立了具有更新機制的鐵路軌道不平順灰色預測模型，用于軌道不平順的劣化預測。然而，GM(1,1)模型在形式上是線性模型[11]，凍脹區軌面幾何不平順受諸多因素的影響，具有較強的非線性特征。GM(1,1)冪模型的灰色作用量中的冪指數能夠較好地反映原始數據的非線性特征，可用于描述和預測事物非線性發展態勢[12-13]。基于此，本文結合某季節性凍土區高速鐵路軌面不平順實測數據，針對其在路基凍脹初始波動、快速發展以及凍脹穩定3個階段的發展規律進行研究，建立了用于凍脹區高速鐵路軌面幾何不平順發展預測的GM(1,1)冪模型，求解了模型的冪指數、優化了初始值和背景值并進行了殘差修正，最后，結合實測數據資料，進行了預測模型的驗證和分析。

1高速鐵路凍脹區軌面不平順發展特征

路基凍脹將引起軌下基礎的變形和破壞，進而影響軌面幾何狀態的變化。通過對我國某高速鐵路2012～2013年70處監測點軌面幾何不平順數據隨時間變化趨勢的分析表明，路基凍脹引起的軌面幾何不平順具有大致相同的變化趨勢。圖1所示為該線路某一典型區段路基凍脹引起的軌面不平順幅值的發展變化情況。由圖1可見，在一個凍脹周期內，高速鐵路凍脹區軌面幾何不平順隨時間的發展歷程大致可分為凍脹初始波動、快速發展、凍脹穩定、快速回落4個階段。該監測點在2012年11月29日至2013年1月29日這2個月內，受氣溫波動的影響，路基開始發生凍脹變形，由此使得軌面不平順隨之發展變化，其幅值變化范圍在1.5 mm以內。而在2013年的1月29日至3月3日期間，隨著氣溫的持續下降，路基凍深增加，凍脹變形加快發展，軌面不平順隨之快速增加，在約一個月的時間內，幅值快速增長至4.8 mm。進入3月份初期，氣溫有所回升，但是路基依然凍結，在該階段，持續時間較短，軌面不平順在0.2 mm的范圍內波動。隨著氣溫的持續升高，凍結的路基開始融化，軌面不平順幅值隨之快速回落，僅用13 d的時間，就隨時間近似呈線性關系由4.98 mm回落至1.12 mm。

圖1　路基凍脹引起的軌面不平順發展特征Fig.1 Development characteristics of track irregularity caused by subgrade frost heaving

為了全面描述該線路由路基凍脹引起的軌面不平順隨時間的發展情況，圖2給出了該高速線路70處監測點在4個階段軌面不平順變化率的統計情況。由圖2(a)可以看出，在凍脹初始波動階段，高速鐵路路基剛開始凍結，軌面不平順幅值波動較小，不平順發展率主要集中在-0.02～0.025 mm/d。隨著氣溫的持續下降，路基的凍脹變形進入快速增長階段，導致軌面不平順隨時間快速增加，其發展變化率集中在0.05～0.2 mm/d(見圖2(b))，較第一階段明顯增大。在凍脹穩定階段，路基表層的凍脹變形基本穩定，軌面不平順幅值在較小的區間內波動，其不平順的發展變化率集中在-0.025～0.04 mm/d(圖2(c))，不平順發展變化率與第一階段類似。隨著氣溫的逐漸升高，路基出現融沉，軌面不平順與時間近似呈線性關系急劇回落，變化率約為-0.4～-0.1 mm/d，如圖2(d)所示。

(a)凍脹初始波動階段;(b)凍脹快速發展階段;(c)凍脹穩定發展階段;(d)快速回落階段圖2　凍脹區軌道不平順變化率分布圖Fig.2 Variation rate distribution of track irregularity in frozen ground region

由此可見，與常規線路不平順的發展惡化趨勢相比，由路基凍脹引起的軌面幾何不平順具有發展速率快，發育、消亡周期短等特點，其發展變化具有明顯的非線性、隨機性特征。高速鐵路凍脹區軌面不平順的形成和發展受路基土質情況及其含水量、大氣溫度、荷載、軌道結構等諸多因素的共同作用[1]，無法確定和量化各因素對軌面幾何不平順發展的隨機作用。而灰色系統理論恰好針對此類部分信息已知、部分信息未知的不確定性系統，僅利用系統行為數據序列建立預測模型，深入挖掘數據的發展規律，實現對系統運行行為演化規律的正確描述，進而實現對其未來變化的定量預測。因此，作者采用灰色系統理論，建立預測模型，進行凍脹區高速鐵路軌面幾何不平順發展預測研究。

2灰色GM(1,1)冪模型的建立與求解

所采用的灰色GM(1,1)冪模型[6]對數據進行了前處理以提高數列的光滑度，利用單位時段差系數修正法將非等時距數列變化為等時距數列，然后利用粒子群智能算法求解了冪指數并優化了初始值和背景值，并對殘差進行了組合修正，具體步驟如下。

2.1灰色GM(1,1)冪模型

2.1.1數據前處理

設凍脹區高速鐵路軌面不平順的檢測數據為

Y(0)={y(0)(t1)、y(0)(t2),...,y(0)(tn)}

(1)

式中，y(0)(ti)非負。

(2)

然后進行函數cotx變化得到非等時間數據序列

X(0)={x(0)(t1)、x(0)(t2),...,x(0)(tn)}

(3)式中，x(0)(ti)=cot(y(0)′(ti)),i=1,2,...,n。

2.1.2等時間間隔處理

傳統的GM(1,1)冪模型是以等時間間隔數據序列為基礎，但是在實際的工程中，由于軌檢車的數據采集時間不固定，所采集的軌面不平順數據是非等時距數列，即所對應的時間序列間距Δti=ti+1-ti≠const,i=1,2,...,n。本文利用單位時段差系數修正法[15,16]對建模數據進行處理從而得到等時間間隔的數據序列

X1(0)={X1(0)(1)、X1(0)(2)，…，X1(0)(N)}

(4)

2.1.31-AGO序列生成

對經過處理的等時間間隔數據點做一次累加生成1-AGO序列

X(1)={x(1)(1)、x(1)(2),...,x(1)(n)}

(5)

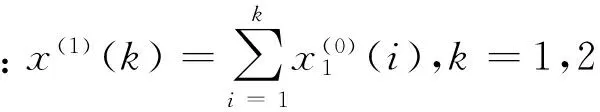
2.1.4初值優化

傳統的灰色建模過程中認為擬合曲線經過初始值x(0)(1)，即用建模的第1個數據作為初值，但是在實際的預測模型中，最優的擬合曲線不一定經過建模數據的某一個點。因此，本文采取給初值一個待優化的初始激擾φ，即用x1(1)=x0(1)+φ作為優化模型的初值。

2.1.5模型方程建立

對生成后的x(1)(k)建立GM(1,1)冪模型的灰色微分方程：

x(0)(k)+az(1)(k)=b(z(1)(k))γ

(6)

式中:z(1)(k)為灰導數背景值；a為發展系數，體現模型的發展態勢；b為灰色作用量，反映數據變化的不確定關系。

2.1.6背景值優化

模型的擬合與預測精度取決于冪指數γ、發展系數a和灰色作用量b，而這三者的求解又與背景值z(1)(k)的構造形式有關，使得背景值成為影響模型精度的關鍵因素。傳統模型中背景值的求解是取兩點的平均值。但是，這種近似降低了GM(1,1)冪模型的精度，為了提高灰色模型精度，本文以

z(1)(k+1)=ψ*x(1)(k+1)+

(1-ψ)*x(1)(k),ψ?(0,1)

(7)

為背景值建立新的模型，其中ψ為背景值待優化系數。

2.1.7時間響應序列求解

對灰色微分方程做最小二乘估計可得參數列

(8)

其中

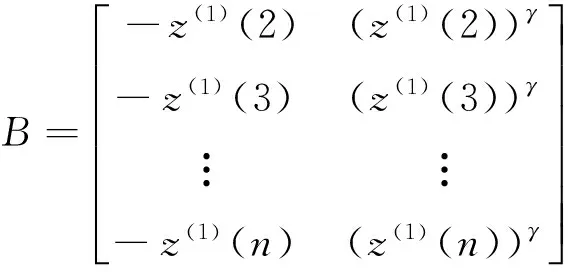
(9)

將式(8)展開可得到γ與a，b的關系式[13]：

a=

(10)

b=

(11)

式(6)的時間響應式

(12)

還原為非等間距數列中與時間t有關的函數

(13)

故可得到各時點的模擬、預測值：

(14)

式中：Δt0為平均時間間隔。

將得到的各時點的模擬、預測值還原到標準化數據：

(15)

最后，將標準化值還原至非標準化值，即為軌面不平順的實際擬合、預測值

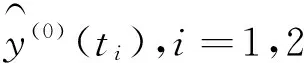
(16)

2.2基于粒子群算法的GM(1,1)冪模型參數

優化

粒子群算法是一種基于群體的隨機優化技術，具有群體智能、迭代格式簡單、可快速收斂到最優解所在區域等優點[17]。根據2.1節所建立的模型，可知共有3個待求解模型參數，即冪指數γ、初值優化激擾φ以及背景值優化系數ψ。為了利用粒子群優化算法求解GM(1,1)冪模型中的模型參數，定義該模型的平均相對誤差函數為：

(17)

這樣GM(1，1)冪模型中參數優化問題可變為利用粒子群算法求解minf(γ,φ,ψ)。

2.3殘差序列的修正

利用上述灰色GM(1,1)冪模型可對軌面不平順的發展趨勢進行擬合預測，但擬合出的趨勢曲線通常是光滑的，不具有波動特征。而其殘差序列通常在零值附近波動，具有不太規律的周期性，說明原始數據隱含有一定的周期性成分和隨機成分。采用諧波變換生成的周期性函數能反映出隨機波動中的大部分周期性成分，正弦函數則反映出隨機波動中殘留的小部分隨機波形成分[7]。本文為提高模型的預測精度，采用諧波變換生成的周期性函數與正弦函數相結合[8]對殘差進行組合修正。

設殘差序列為：

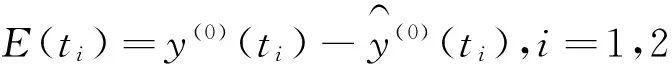
(18)

利用諧波變換生成的周期序列函數對E(ti)進行擬合

i=1,2...,n

(19)

利用殘差序列波形平均特征構造正弦殘差修正周期函數，其模型為

(20)

引入權重系數α和β對式(19)和(20)進行權重組合得到殘差的組合修正模型為

(21)

式中: α+β=1，α和β的取值以同樣模型數據的平均相對誤差最小為原則確定。

最終得到的GM(1，1)冪修正模型為：

(22)

2.4模型的后驗差檢驗

為檢驗所建立模型的準確性和可靠性，用后驗差檢驗方法[18]對其進行精度檢驗和預測值精度估計。一般，根據小誤差概率P和均方差比值C的大小，將預測精度分為4類，如表1所示。

表1　精度檢驗等級參照表

3算例分析

應用2012年11月至2013年1月某高速鐵路K147.548 km處軌面不平順實際檢測數據，進行了基于GM(1,1)冪模型的高速鐵路凍脹區軌面不平順發展預測分析，借此驗證了模型的可行性與可靠性。所選用的軌面不平順原始數據如表2所示。

取前15組數據樣本建立模型，將原始數據經過標準化(開4次方)處理，按照上述步驟求解得到冪指數γ=1.332 1，背景值優化系數ψ=0.469 5，初值優化激擾φ=-0.002 8。最后計算得到的擬合結果如圖3和表3所示。

圖3　軌面不平順實測值與擬合值曲線對比Fig.3 Curve comparison between tested values and fitted values of track irregularity

由圖3和表3可以看出，所建立的GM(1,1)冪模型能夠模擬凍脹區軌面不平順隨時間的變化情況，擬合精度較高。預測模型的后驗差檢驗結果為：均方差比值C=0.074 1，小誤差概率P=1，精度等級為一級，擬合值的平均相對誤差為1.46%，擬合值平均絕對誤差為0.028。由此說明，該模型擬合精度較高，能夠用于外推預測。

利用所建立的預測模型對上述所選取路段2013年1月14至2013年1月29日所檢測的5組數據進行了預測，并與實測數據進行了對比，其結果如表4所示。由表4結果可見，預測值的平均相對誤差為4.56%，平均絕對誤差為0.212，模型的預測值與實測值較為接近，預測精度較高。

表2　高速鐵路凍脹區軌面不平順實測值

表3軌面不平順實測值與擬合值的數值比較

Table 3 Numerical comparison between tested values and fitted values of track irregularity

序號相對時間實測數據擬合數據殘差相對誤差102.112.0970.0130.62%292.372.3580.0120.51%3111.891.897-0.0070.37%4131.841.7960.0442.39%5151.641.640006171.751.7260.0241.37%7191.641.678-0.0382.32%8211.361.385-0.0251.84%9251.221.226-0.0060.49%10291.921.8420.0784.06%11321.911.8300.0804.19%12341.962.000-0.0402.04%13362.172.174-0.0040.18%14402.862.875-0.0150.52%15433.073.0380.0321.04%

表4軌面不平順實測值與預測值的比較

Table 4 Comparison between tested values and predictive values of track irregularity

序號相對時間實測數據擬合數據殘差相對誤差16463.443.454-0.0140.41%17494.13.8000.3007.32%18524.484.1780.3026.74%19595.314.9550.3556.69%20615.415.3210.0891.65%

此外，將該高速線路70余處凍脹監測點的不平順數據按時間序列生成128組有效數據樣本，利用所建立的GM(1,1)冪模型對這些樣本數據進行了擬合和預測。圖4所示為這128組樣本數據的擬合和預測值平均相對誤差的統計情況。由圖4結果可以看出，擬合值的平均相對誤差集中在1%～8%之間，平均值約為5.64%；預測值的平均相對誤差集中在2%～8%之間，平均值約為6.47%。由此進一步說明，本文所建立的模型具有較高的擬合與預測精度，可以用于凍脹區高速鐵路軌面不平順發展預測之用。

(a)擬合值平均相對誤差;(b)預測值平均相對誤差圖4　擬合和預測值平均相對誤差分布圖Fig.4 Mean relative error distribution of fitted values and predictive values

上述計算和分析結果表明，所建立的GM(1,1)冪模型能夠利用高速鐵路凍脹區40 d左右的不平順數據較為準確地預測未來10～20 d的不平順變化情況，如此可為高速鐵路凍脹區軌道的養護維修提供一定的緩沖時間，有助于工務部門合理的制訂和實施養護維修計劃。

4結論

1)凍脹區高速鐵路路基凍脹引起的軌面幾何不平順與常規線路軌面幾何不平順相比具有發展速率快，發育、消亡周期短等特點，其發展變化具有明顯的非線性、隨機性特征。

2)采用基于粒子群算法的GM(1,1)冪模型，能夠模擬和預測路基凍脹從發生到穩定這一過程中，軌面不平順在諸多影響因素共同作用下隨時間的發展惡化過程。

3)模型中的冪指數能夠較好的模擬軌面不平順在路基凍脹過程中的非線性發展態勢。

4)本模型為解決凍脹區高速鐵路軌面不平順發展因素的不確定性因果關系和對軌面不平順發展進行中短期預測提供了一種方法。在保障高速鐵路的安全運營、實現預防性計劃維修等方面能夠為工務部門提供參考。

參考文獻：

[1] 杜曉燕, 葉陽升, 張千里, 等. 季節性凍土區高速鐵路路基凍深研究[J]. 中國鐵道科學, 2015, 36(2): 11-17.

DU Xiaoyan, YE Yangsheng, ZHANG Qianli, et al. Freezing depth of high speed railway subgrade in seasonally frozen ground region[J]. China Railway Science, 2015, 36(2): 11-17.

[2] 王天亮. 寒區路基改良土力學特性分析[M]. 北京: 中國鐵道出版社, 2014.

WANG Tianliang. Mechanical properties analyses of the roadbed improved soil in cold regions[M]. Beijing: Chinese Railway Press, 2014.

[3] 張先軍. 哈大高速鐵路路基凍脹規律及影響因素分析[J]. 鐵道標準設計, 2013, (7): 8-12.

ZHANG Xianjun. Analysis of frost heave laws in subgrade on Haerbin-Dalian high-speed railway and its influence factors[J]. Railway Standard Design, 2013, (7): 8-12.

[4] 羅林. 輪軌系統軌道平順狀態的控制[M]. 北京:中國鐵道出版社, 2006.

LUO Lin. Control of track irregularity state of wheel / rail system[M]. Beijing: Chinese Railway Press, 2006.

[5] 黃新文, 崔俊杰, 易菊香. 吉琿客運專線路基凍脹變形及影響因素分析[J]. 鐵道標準設計, 2015, 59(8): 39-42.

HUANG Xinwen, CUI Junjie, YI Juxiang. Analysis of frost heave deformation of the subgrade on Jilin-Hunchun dedicated passenger railway line[J]. Railway Standard Design, 2015, 59(8): 39-42.

[6] 黨耀國. 灰色預測與決策模型研究[M]. 北京: 科學出版社, 2009.

DANG Yaoguo. Research on grey prediction and decision-making model[M]. Beijing: Science Press, 2009.

[7] 曲建軍, 高亮, 張新奎, 等. 基于灰色GM(1,1)非等時距修正模型的軌道質量預測[J]. 中國鐵道科學, 2009, 30(3): 5-8.

QU Jianjun, GAO Liang, ZHANG Xinkui, et al. A prediction method for track quality based on grey GM(1,1) non-equal time interval correction model[J]. China Railway Science, 2009, 30(3): 5-8.

[8] 曲建軍, 高亮, 田新宇, 等. 基于灰色理論的軌道幾何狀態中長期時變參數預測模型的研究[J]. 鐵道學報, 2010, 32(2): 55-59.

QU Jianjun, GAO Liang, TIAN Xinyu， et al. Study on the mid&long term prediction model of track geometry state based on the grey time-varying parameters theory[J]. Journal of the China Railway Society, 2010, 32(2): 55-59.

[9] 張玉芝, 杜彥良, 孫寶臣. 改進的動態灰色模型在高鐵路基變形預測中的應用[J]. 鐵道科學與工程學報, 2013, 10(2): 56-61.

ZHANG Yuzhi, DU Yanliang, SUN Baochen. Application of improved dynamic grey model in high-speed railway bed settlement prediction[J]. Journal of Railway Science and Engineering, 2013, 10(2): 56-61.

[10] 郭然, 韓寶明, 李得偉, 等. 具有更新機制的鐵路軌道不平順灰色預測模型[J]. 中南大學學報(自然科學版), 2013, 44(10): 4334-4341.

GUO Ran, HAN Baoming, LI Dewei, et al. Grey prediction model for track irregularity with update mechanism[J]. Journal of Central South University(Science and Technology), 2013, 44(10): 4334-4341.

[11] 王正新, 黨耀國, 劉思峰,等. GM(1,1)冪模型求解方法及其解的性質[J]. 系統工程與電子技術, 2009, 31(10): 2380-2383.

WANG Zhengxin, DANG Yaoguo, LIU Sifeng, et al. Solution of GM(1,1) power model and its properties[J]. Systems Engineering and Electronics, 2009, 31(10): 2380-2383.

[12] 李軍亮, 肖新平, 廖銳全. 非等間隔GM(1,1)冪模型及應用[J]. 系統工程理論與實踐, 2010, 30(3): 490-495.

LI Junliang, XIAO Xinping, LIAO Ruiquan. Non-equidistance GM(1,1) power and its application[J].Systems Engineering-Theory&Practice, 2010, 30(3): 490-495.

[13] 王正新, 黨耀國, 劉思峰. 非等間距GM (1,1)冪模型及其工程應用[J]. 中國工程科學, 2012, 14(7): 98-102.

WANG Zhengxin, DANG Yaoguo, LIU Sifeng. Non-equidistant GM(1,1) power model and its application in engineering[J]. Engineering Sciences, 2012, 14(7): 98-102.

[14] 李翠鳳, 戴文戰. 基于函數cotx變換的灰色建模方法[J]. 系統工程, 2005, 23(3): 110-114.

LI Cuifeng, DAI Wenzhan. An approach of the grey modelling based on cotxtransform action[J]. Systems Engineering, 2005, 23(3): 110-114.

[15] 黃聲享, 李志成. 工程建筑沉降預測的非等間距灰色建模[J]. 地理空間信息, 2004, 2(1): 41-43.

HUANG Sengxiang, LI Zhicheng. Grey modeling of non-equidistant data sequent for forecasting subsidence of the engineering buildings[J]. Geospatial Information, 2004, 2(1): 41-43.

[16] 梅紅, 孫澤信. 非等間距GM(1,1)模型的改進及預測分析[J]. 河海大學學報(自然科學版), 2010, 38 (5): 569-574.

MEI Hong, SUN Zexin. Improvement and prediction of non-equal interval GM(1,1) model[J]. Journal of Hehai University(Natural Sciences), 2010, 38(5): 569-574.

[17] 高飛. Matlab智能算法超級學習手冊[M]. 北京:人民郵電出版社, 2014.

GAO Fei. Super learning manual of Matlab intelligent algorithm [M]. Beijing: Posts&Telecom Press, 2014.

[18] 羅佑新. 灰色系統理論及其在機械工程中的應用[M]. 長沙: 國防科技大學出版社, 2001.

LUO Youxin. Grey system theory and its application in mechanical engineering[M]. Changsha: National University of Defense Technology Press, 2001.

Track irregularity evolution prediction for high speed railways in frozen ground region based on GM(1,1) power model

GUO Yi, GAO Jianmin

(State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China)

Abstract：According to the evolving characteristics of track irregularity of high speed railway in frozen ground region, the non-equal interval GM(1,1) power model was established based on the grey system theory. When establishing the GM(1,1) model, the track irregularity test data of high speed railway in frozen ground region were treated as the time series. The initial values and background values of the model were optimized to improve the prediction accuracy. The power exponent was solved by using particle swarm intelligence algorithm. In order to fit the random components of track irregularities better, periodic functions generated by harmonic transform and sine function were introduced to modify the residual error. Accordingly, the track irregularity evolution of high speed railway in frozen ground region during the process of the subgrade frost heaving was predicted. The results show that the model can well reflect the time-dependent random fluctuation characteristics of track irregularity evolution of high speed railway in frozen ground region. The average relative error of the fitted values is 5.64% and the average relative error of the predictive value is 6.47%. This model may provide references for the maintenance of track irregularity of high speed railway in frozen ground region.

Key words：high speed railway；track irregularity；subgrade frost heaving；GM(1,1) power model；development prediction

收稿日期：2015-11-12

基金項目：國家重點基礎研究發展計劃(973計劃)項目(2013CB036205，2013CB036206)；中國鐵路總公司科技研究開發計劃資助項目(2014G001-1)；中央高校基本科研業務費專項資金資助項目(2682015CX045)；牽引動力國家重點實驗室自主研究資助項目(2014TPL_T01)

通訊作者：高建敏(1981-)，女，河北南和人，副研究員，博士，從事鐵路軌道不平順及其管理研究；E-mail：jmgao@swjtu.edu.cn

中圖分類號：U212.2

文獻標志碼：A

文章編號：1672-7029(2016)05-0791-09