初中數學幾何教學證明中“基本圖形”的作用分析

汪德

中圖分類號：G633.6 文獻標識碼：B文章編號：1672-1578（2016）06-0244-01

在初中階段，學習幾何基本知識至關重要，要引導學生學習基本的幾何定義、公理等，借助"基本圖形"，逐漸培養學生邏輯思維能力、抽象思維能力等，提高他們分析、解決問題的能力，促進他們的全面發展。以此，改變初中數學教學現狀，提高課堂教學效率與質量。

1.簡化教師幾何教學方法，拓展學生思維

在初中幾何教學中，想要提高學生解題效率，縮短幾何題證明時間，必須準確了解不同類型的幾何圖形，要引導學生把基本圖形從復雜圖形中分解出來，記住必要的基本圖形性質，便能把復雜的圖形簡單化，降低題目難度。在初中幾何教學中，"互為鄰補角的兩個角品分線互相垂直"這一結論是學生必須正確理解、掌握的。同時，在適當延伸、拓展基本圖形的基礎上，能夠進一步拓展學生思維，也能在一定程度上簡化教師的幾何教學方法。在"基本圖形"作用下，關于角平分線題目思路也會更加清新，解題過程更加簡單，具有較好的化難為易的作用，學生也能準確理解、掌握新的知識點。

例如：∠AOB、∠BOC為鄰補角，OD、OE為∠AOB、∠BOC的平分線，得出OD⊥OE。下面是相關的圖形。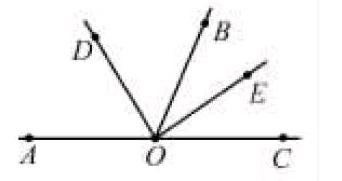

在角平分線教學中，教師可以借助該基本圖形來簡化相關的證明過程，迅速找到解題的突破口，提高解題速度與準確率。

例如：小東根據提示，畫出了45度的角，即：需要先做出兩條相互垂直的直線MN、PQ，點A、B是直線MN、PQ上的任意一點，需要作出∠ABP的平分線，即BD，并將其反向延長，和∠OAB平分線相交于點C，而∠C就是所求的45度角。請問是否正確，并進行證明。下面是相關的圖形。

對于這道題來說，圖形復雜化，題中的條件也非常零亂，但仔細審題，便能發現題目中的核心條件，即兩條角平分線，這就是解題的關鍵所在。在解答該題的時候，學生可以根據相關定理的基本圖形，適當簡化圖形，并借助圖形變換，加入一些關鍵性圖形，解題思路也更加清晰，迅速找到突破口，提高解題正確率。還能拓展學生的思維，做到舉一反三，學以致用，不斷培養他們的數學思維。

2.巧妙引入其他知識點，培養學生創新素養

例如：B是直線DF上的某點，∠ABC和Rt∠相等，以A、C兩點為基點，做直線的垂線，D、E是對應垂足。那么，△ABD ∽△BCE，如果AB和BC相等，△ABD ≌△BCE。下面是相關的圖形。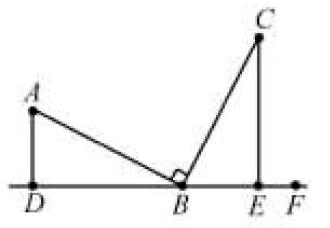

對于該圖形來說，學生大都非常熟悉，分別在全等三角形、相似三角形中出現，只是沒有兩線段相等的相關條件。在反復練習中，大部分學生都能靈活應用該基本圖形。在此基礎上，教師需要根據學生掌握情況，把其他相關知識點巧妙地融入到該圖形中，使其相互融合，引導學生進一步深入思考，為培養他們的創新思維做好鋪墊。

例如：已知正三角形ABC的邊長為8，其中BD為3，角ADF的度數為60度，請求出AE的長度。下面是相關的圖形。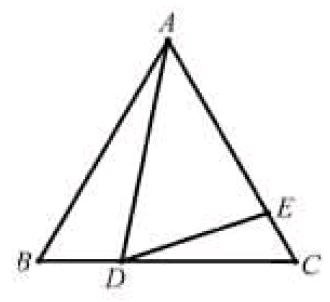

就該題來說，該圖形是在基本圖形基礎上得出的，基本圖形中的直角三角形已經變為等邊三角形，也就是說將對應角從90度變為60度，其他條件都沒有任何變化，和原題有著相同的解題思路。簡單來說，學生只要掌握了基本圖形的解題方法，便能迅速找到解答該題的突破口，正確解答該題。為此，在幾何知識教學中，教師要讓學生充分意識到基本圖形的重要性，準確理解、掌握相關知識點，并巧妙地應用到各類變形題中，基本圖形拓展題中，把知識學活，轉化為自己的知識點。

3.結語

總而言之，在初中幾何教學中，教師要對"基本圖形"引起重視，要優化利用不同類型的"基本圖形"，不斷深入研究各類基本圖形，結合初中生的興趣愛好、個性特征、心理特征等，優化幾何教學方法，巧妙地引入其他相關知識，和圖形有機融合，不斷拓展學生思維，引導他們積極思考，培養他們的創新素養，逐漸提高學生靈活運用各類基本圖形有效解決對應的幾何問題。以此，更好地發揮"基本圖形"在初中幾何課堂教學中所起的作用，提高課堂教學有效性。