壓印機入口坯餅柔性分散機構的開發研究

丘盛昌,　安　琦

(華東理工大學機械與動力工程學院,上海 200237)

壓印機入口坯餅柔性分散機構的開發研究

丘盛昌,安琦

(華東理工大學機械與動力工程學院,上海 200237)

摘要：針對壓印機在生產過程中出現的坯餅團聚問題,開發了一種利用彈簧為攪拌元件的柔性分散機構,通過豎直懸掛的若干個彈簧對硬幣的彈撥作用,實現坯餅的有效分散功能。通過力學建模,建立了這種柔性分散機構的碰撞分離模型以及彈簧尺寸參數的優化模型,結合一個壓印機的具體結構參數,采用懲罰函數法(SUMT)對優化模型進行了數值模擬優化,得到分散機構工作彈簧的最佳尺寸參數,實驗證明該分散機構具有良好的分散效果。

關鍵詞：壓印機; 坯餅團聚; 分散機構; 參數優化; 懲罰函數法

硬幣的生產事關國家的經濟命脈,硬幣生產的關鍵設備是壓印機。壓印機在實際工作中常常出現輸餅轉盤中坯餅的團聚現象,坯餅以層疊的形式隨著轉盤轉動，由于在滑道的入口處存在高度限制,這些層疊的坯餅無法順利進入滾道,因此可能出現堵塞滑道入口現象,進而影響生產的正常進行。目前有許多學者對壓印機進行了研究,包括壓印機的結構設計及運動仿真[1-2]、壓印精度的提高[3-4]、壓印機的動力系統[5]等,但鮮見對坯餅進口的團聚現象進行研究。

通過調研發現,現有的一些分離機構并不能很好地滿足對團聚的坯餅的有效分離[6-8]。因此本文構建了一種用彈簧作為柔性攪拌元件的柔性攪拌機構,并通過對彈簧的優化設計,實現了壓印機入口硬幣的有效分散。

1坯餅團聚現象分析

圖1所示為某企業進行硬幣生產所采用的某型號臥式壓印機,其工作原理見圖2。在工作時,一批坯餅傾倒在旋轉的輸餅轉盤上,由于離心力的作用,坯餅被甩到輸餅轉盤的邊緣并被外殼體限制徑向位置;坯餅在輸餅轉盤的邊緣和轉盤一起運動,當到達外殼體上的出口也即滑道入口時,坯餅被甩離轉盤進入滑道,順著滑道下滑進入壓印模具,在中圈承受來自左模和右模的壓力產生變形,壓印完成后由旋轉的中圈將成品送到出口,進入后續的輸送部件。

圖1　某型號壓印機結構圖

圖2　壓印機工作原理圖

在生產過程中常常發現輸餅轉盤中的坯餅聚集成堆而難以分離,并且始終以層疊的方式隨著轉盤轉動。由于在滑道的入口處存在高度限制,這些層疊的坯餅無法順利進入滾道,并且可能出現圖3所示的堵塞滑道入口的情況,從而影響生產的正常進行。為此需要構建坯餅進口分散機構,確保坯餅在轉盤上的有效分散。

2分散機構的構建原理

為了解決壓印機入口處坯餅團聚問題,本文根據坯餅的堆積情況,構建了一種利用彈簧的彈撥作用而形成的一種柔性打散機構，具體方案如圖4所示。將壓縮彈簧用支架固定在輸餅轉盤的上方,彈簧與機架固定,彈簧底端與轉盤的距離始終保持在介于一個坯餅和兩個坯餅之間的厚度,坯餅在摩擦力的作用下隨著轉盤運動,并與彈簧碰撞,彈簧由于坯餅的作用,始終處于往復振動狀態,對坯餅不斷擊打,從而實現坯餅的分離。這樣的原理類似于一個攪拌器,彈簧類似于其中的攪拌槳,這種攪拌是一種柔性攪拌過程。

圖3　滑道入口堵塞情況示意圖

圖4　分散機構原理圖

3機構建模及性能參數優化

3.1分散機構等效圖及尺寸參數

本文設計的柔性攪拌機構能否實現最有效的分散功能,關鍵在于彈簧參數的選取,包括彈簧圈數、簧絲直徑、節距、彈簧中徑等參數。為此,通過力學建模和數值模擬優化,對彈簧參數進行了深入研究。

本文所構建的柔性攪拌機構的核心元件是彈簧,其工作原理及坯餅尺寸如圖5所示。圖中v為轉盤外緣的線速度,L為彈簧長度,me為彈簧自由端等效質量,mp為坯餅質量,dp為坯餅直徑,h為坯餅厚度。坯餅與轉盤之間由于摩擦力作用無相對運動,取x方向為矢量的正方向。

3.2確定彈簧自由端等效質量

圖4所示是一種非線性振動的彈簧質量系統。根據文獻[9],彈簧的高度越高,彈簧質量系統的振動越接近簡諧振動。本文中彈簧具有相當的高度,且僅需考慮1/2個周期,因此將其按簡諧振動處理。假設做簡諧振動的彈簧質量系統中彈簧的總質量為m,則彈簧的等效質量me為[10-13]

圖5　分散機構等效圖及尺寸參數

(1)

其中:ρ為彈簧鋼密度；d為彈簧絲徑；D2為彈簧中徑；n為彈簧圈數；α為彈簧螺旋升角。

3.3第1次碰撞

假設分散機構開始工作時,彈簧處于豎直靜止狀態,坯餅隨著轉盤以一定的速度vp(vp=v)撞上彈簧自由端。假設發生的碰撞為完全彈性碰撞,且能夠使堆積的坯餅分離。碰撞后彈簧自由端產生向左的速度ve1,坯餅速度為vp1,碰撞產生動載荷為Fd1，如圖6所示。

圖6　第1次碰撞過程示意圖

根據動量和能量守恒定律,可得

(2)

碰撞后的彈簧滿足能量守恒,可得

(3)

式中：x1為第1次碰撞彈簧達到最大變形量時自由端的位移；自由端橫向剛度KH=k(x)是自由端位移的函數,也可以根據文獻[14]表示為橫向作用力FH的函數。

坯餅與彈簧之間由于碰撞產生的動載荷為

(4)

式中:g為重力加速度;P為靜載荷,P=mpg;Δst為彈簧在P作用下的靜位移。聯立式(2)和式(3),可得

(5)

3.4第2次碰撞

第1次碰撞結束后,坯料被分離,后續坯餅繼續與彈簧發生碰撞,假設碰撞發生于彈簧回彈到豎直狀態時,則坯餅恰好運動到彈簧的豎直位置。假設碰撞時坯餅速度為vp,彈簧自由端速度為-ve1,碰撞后彈簧自由端得到速度ve2,坯餅速度變為vp2,碰撞產生動載荷為Fd2,碰撞過程如圖7所示。

圖7　第2次碰撞過程示意圖

根據動量及能量守恒定律,可得到第2次碰撞的力學關系為

(6)

不考慮碰撞過程的能量損失,碰撞后的彈簧滿足能量守恒定律

(7)

式中,x2為第2次碰撞彈簧達到最大變形量時自由端的位移。

第2次碰撞產生的沖擊動載荷為

聯立式(6)和式(7)可得

(8)

3.5第3次碰撞

第2次碰撞結束后,坯料被分離,后續坯料繼續與彈簧發生碰撞,同樣假設碰撞發生于彈簧回彈到豎直狀態,這時坯餅恰好運動到彈簧的豎直位置。同樣假設碰撞時坯餅速度為vp,彈簧自由端速度為-ve2,碰撞后彈簧自由端得到速度ve3,坯餅速度變為vp3,碰撞產生動載荷Fd3,如圖8所示。

圖8　第3次碰撞過程示意圖

根據動量及能量守恒定律,可得

(9)

碰撞后的彈簧滿足能量守恒定律

(10)

式中,x3為第3次碰撞彈簧達到最大變形量時自由端的位移。

第3次碰撞產生的動載荷為

聯立式(9)和式(10)可得

(11)

3次碰撞之后,機構將進入穩定的重復運行階段。

由于彈簧自由端從最大位移x3回到平衡位置時的運動是變加速運動,為計算這段位移需要的時間,將這段位移作有限段的等分,每個微段看作勻加速直線運動,可求得彈簧回到平衡位置需要的時間為

(12)

3.6模型優化

要使機構能夠正常工作,第1次碰撞產生的動載荷Fd1應大于坯餅之間的咬合力F,可得優化邊界條件1如下：

根據彈簧絲徑d小于或等于節距p的特征,可得優化邊界條件2如下：

綜上,優化問題的數學模型為

(13)

針對上述模型,采用適當的優化方法進行優化計算。

3.7懲罰函數法

針對式(13)給出的約束優化問題,可用懲罰函數法進行優化計算。懲罰函數法的基本原理是將約束優化問題中的不等式和等式約束函數經過加權轉化后,和原目標結合形成新的目標函數——懲罰函數,并求解該新目標函數的無約束極小值,以期得到原問題的約束最優解[15-16]。由于懲罰函數法具有對方程初始解要求低、迭代收斂速度快的優點[17],簡單實用,在優化計算中具有廣泛的應用。

根據約束形式和構造的函數及懲罰函數因子的不同,懲罰函數法分為內點懲罰函數法、外點懲罰函數法和混合型懲罰函數法3種,其中外點懲罰函數法由于能夠同時解決含有等式和不等式的約束優化問題,而且懲罰函數的構造、初始點的選擇沒有區域限制,具有收斂速度快的優點[18-19],所以本文采用外點懲罰函數法進行優化計算。

4算例分析

某型號的壓印機,由于是在現有的機器上進行改進,使用彈簧的高度L受輸餅轉盤處空間限制只能取70 mm,彈簧的中徑D2受坯餅直徑限制只能取8 mm。根據機器參數及實測數據,轉盤外緣的線速度v=1.87 m/s,坯餅直徑dp=25 mm,厚度h=2.15 mm,質量mp=6.05 g,坯餅之間的咬合力F=0.6 N。現根據前文建立的優化模型,對彈簧的絲徑d,圈數n進行優化,使機構能在最佳狀態下運行。為便于計算,本文中彈簧的圈數n取整數。

根據文獻[20],彈簧的螺旋升角滿足

(14)

18≤n≤31(n∈Z)

因此得2.2≤p≤3.98,根據文獻[20],可得符合要求的絲徑d的取值范圍為

d={0.3，0.35，0.4，0.45，0.5，0.6，0.7，0.8，0.9，

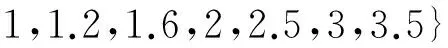
采用外點懲罰函數法對式(13)所示的優化模型進行改寫,可得帶懲罰約束項的目標函數為[19]

(15)

式中,r為懲罰因子。

取懲罰因子r=1 000,根據式(15),按前文求得的圈數及絲徑的取值范圍取不同的絲徑d及圈數n,通過MATLAB編寫計算程序,求得最終結果為:當n=21,d=1.2 mm時,fmin=2.35×10-4s。即當彈簧絲徑為1.2 mm,中徑為8 mm,圈數為21圈時,目標函數最小,此時的尺寸參數為最優值。彈簧最佳尺寸參數如表1所示。按照該組參數設計的壓印機坯餅進口分散機構,目前已經通過實驗驗證,證實具有很好的分散效果,實現了預期的功能。

表1　最佳彈簧幾何參數表

5結論

(1)針對壓印機工作過程中入口存在的坯餅團聚問題,設計了一種利用彈簧為攪拌元件的柔性分散機構,通過豎直懸掛的若干個彈簧對硬幣的彈撥作用,實現坯餅的有效分散功能。

(2)對所構建的壓印機入口坯餅柔性分散機構進行研究,通過力學建模,建立了坯餅和分散機構的碰撞分離模型,并建立了彈簧尺寸參數的優化模型，采用懲罰函數法對優化模型進行了數值模擬優化,得到分散機構工作彈簧的最佳尺寸參數。實驗證實本文設計的柔性分散機構具有良好的分散效果。

參考文獻：

[1]王洪珍.基于Autodesk Inventor11的壓印機結構設計及運動仿真[J].機械研究與應用,2011(6):76-78.

[2]王江濤,周炳海.福格森凸輪曲線的測定與分析[J].機械制造,2006,44(10):69-72.

[3]嚴樂,盧秉恒,丁玉成,等.高精度步進壓印機熱誤差的建模分析[J].西安交通大學學報,2005,39(5):526-530.

[4]嚴樂,盧秉恒,丁玉成,等.高精度壓印機熱誤差補償中溫度變量的辨識[J].西安交通大學學報,2006,40(7):827-830.

[5]張建新.高頻換向快動型壓印機液壓系統的研究[J].山西機械,2001 (3):40-41.

[6]BENSON R B,COURTEAU W J,PAUL S T，etal.Unstacking Machine:4252484(A)[P].1981-2-24.

[7]許健健,王耕耘,王義林.基于NX7.0的一種自動化沖壓生產線板料分離機構的設計[J].鍛壓裝備與制造技術,2012(1):13-16.

[8]彭國慶,陳柏金.基于氣動機械手的自動化沖壓生產線的設計[J].鍛壓技術,2012,37(3):85-88.

[9]黃焱,何松林.彈簧質量系統非線性振動的實驗研究[J].昆明學院學報,2014,36(6):66-68.

[10]丁履成,司明揚.有質量的彈簧的振動問題[J].大學物理,1985(9):15-19.

[11]羅蔚茵.關于彈簧振子固有頻率的進一步討論[J].大學物理,1985(11):9-11.

[12]孫春峰.彈簧的質量、材料及其幾何性質對彈簧諧振子角頻率的影響[J].大學物理,1993(12):20-21.

[13]劉大鵬,關榮華.彈簧質量對彈簧諧振子圓頻率的影響[J].大學物理,1995(10):22-24.

[14]丘盛昌,安琦.圓柱螺旋彈簧橫向剛度的計算方法研究[J].華東理工大學學報(自然科學版),2015,41(6):846-851.

[15]安琦,顧大強.機械設計[M].北京:科學出版社,2008:400-420.

[16]孫靖民,梁迎春.機械優化設計[M].北京:機械工業出版社,2006:145-151.

[17]HAN S P,MANGASARIAN O.Exact penalty functions in nonlinear programming[J].Mathematical Programming,1979,17(1):251-269.

[18]何力,王琴芳.懲罰函數法在發動機性能計算中的應用[J].南京航空航天大學學報,2001,33(4):338-341.

[19]殷曉飛,任曉丹.基于VB外點懲罰函數法的實現[J].裝備制造技術,2011(3):64-66.

[20]MOHAMMAD R T,FEREIDOUN A.Optimizing structural active control force using the exterior penalty function method[J].AIP Conference Proceedings,2008,1020(1):1245-1252.

Blank Dispersing Mechanism for Stamping Machine

QIU Sheng-chang,AN Qi

(School of Mechanical and Power Engineering,East China University of Science and Technology,Shanghai 200237,China)

Abstract:Stacking blank in stamping machine was studied and a blank dispersing mechanism using springs hanged above the stacking blank to disperse was developed.The model of the collision between the blank and the spring was established through the mechanical analysis.Based on the collision model,the optimized model for selecting spring was established,and on the basis of the parameters of a stamping machine,the SUMT was used to numerically calculate the optimized model and the optimum parameters of the spring which was used in the dispersing mechanism were obtained.The developed blank dispersing mechanism was proved to work well through experiment.

Key words:stamping machine; stacking of blank; dispersing mechanism; parameter optimization; SUMT

收稿日期：2015-06-15

作者簡介：丘盛昌(1990-),男,福建人,碩士生,研究方向為機械設計及理論。 通信聯系人：安琦,E-mail:anqi@ecust.edu.cn

文章編號：1006-3080(2016)02-0291-06

DOI:10.14135/j.cnki.1006-3080.2016.02.022

中圖分類號：TH135+.1

文獻標志碼：A