多軸應力條件下壓力管道的熱棘輪極限

張紅才,　鄭小濤,　彭紅宇,　軒福貞,　王正東

(1.華東理工大學承壓系統與安全教育部重點實驗室,上海 200237;2.武漢工程大學機電工程學院,武漢 430205; 3.中國石化湖北化肥分公司,湖北 枝江 443200)

多軸應力條件下壓力管道的熱棘輪極限

張紅才1,3,鄭小濤2,彭紅宇2,軒福貞1,王正東1

(1.華東理工大學承壓系統與安全教育部重點實驗室,上海 200237;2.武漢工程大學機電工程學院,武漢 430205; 3.中國石化湖北化肥分公司,湖北 枝江 443200)

摘要：通過非循環理論方法推導出了多軸應力條件下壓力管道的熱棘輪極限解析解,并討論了軸向壓縮應力對棘輪極限的影響,提出了相應的設計方法,并采用簡化有限元方法進行了驗證。結果表明,軸向壓縮應力會顯著降低多軸載荷下壓力管道的棘輪極限,本文的理論解與有限元分析結果吻合良好,與只考慮內壓引起的環向應力和軸向應力情況相比,本文的解析解更加精確。這說明本文設計方法可用于評估壓力管道及類似工況下結構的棘輪極限,具有一定的工程價值。

關鍵詞：棘輪極限; 壓力管道; 多軸載荷; 非循環方法

熱棘輪是循環熱-機械載荷下核電及化工壓力管道的主要失效模式之一。近年來,基于失效模式的分析設計方法逐漸被認可并被推廣應用,限制棘輪失效的棘輪極限設計方法顯得日益迫切。Bree[1]將薄壁圓筒簡化為僅考慮環向應力的單軸模型,首次建立了薄壁圓筒熱棘輪設計方法,即Bree圖。隨后,Bree進一步推導了考慮雙軸應力下的薄壁管道的熱棘輪極限[2]。但上述方法僅能分析軸向拉伸應力的情況,并不包括軸向壓縮應力情況。已有研究[3]表明,軸向壓縮載荷會顯著降低結構的熱棘輪極限,但研究結果均為有限元解[3-4],尚缺乏精確的理論解。近來。Reinhardt和Adibi-Asi[5]針對單軸載荷和多軸問題[6-7]提出了非循環方法,可用于研究復雜條件下結構的棘輪極限。本文在此基礎上,推導了多軸條件下壓力管道棘輪極限解析解,并提出了相應的設計方法。

1理論基礎

假設壓力管道為理想彈塑性材料,在承載過程中服從小應變和von Mises屈服條件。在本文分析過程中,將循環載荷組合分為穩態載荷和隨時間變化的循環載荷[5],則通過結構橫截面的剩余等效承載力以及在剩余強度條件下對穩態載荷的極限承載能力分別如式(1)和式(2)所示。

(1)

(2)

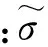
2棘輪極限理論分析

2.1兩端封閉壓力管道棘輪極限分析

假定壓力管道承受的組合載荷可分為穩定內壓載荷Pi、軸向壓縮載荷Pc和循環線性溫度梯度載荷ΔT,Ro和Ri分別是管道外半徑與內半徑，如圖1(a)所示，如圖1(b)示出了壓力管道的載荷工況。

在穩定內壓載荷Pi和循環的線性溫度梯度載荷ΔT作用下兩端封閉的壓力管道承受著Pi和ΔT的組合載荷。假設承受線性溫度梯度兩端封閉的壓力管道呈等雙軸應力狀態，當循環熱應力沿整個厚度保持彈性,環向應力和軸向應力為

(3)

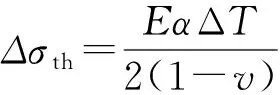
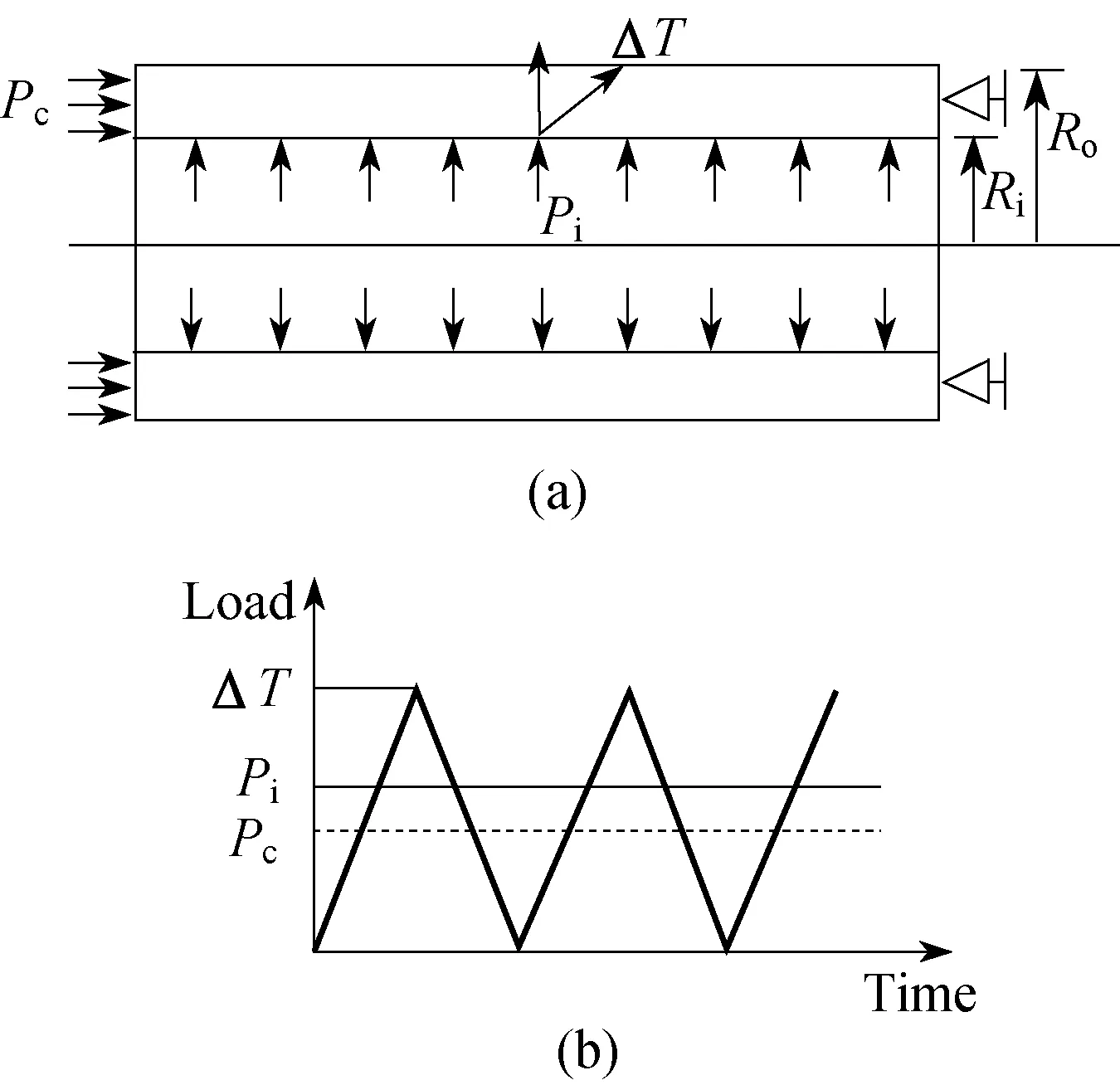
圖1　壓力管道的載荷工況

隨著線性溫度梯度的增加,圓筒的內、外表面會首先出現屈服,且屈服區域隨溫度梯度的增加而增大。當發生屈服時,圓筒的熱應力分布如下:

(4)

式中,rep為外纖維屈服的厚度。

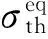
當循環熱應力沿整個厚度保持為彈性時,相應的等效應力為

(5)

當發生屈服時,相應的等效應力為

(6)

(7)

(8)

當熱循環應力沿整個厚度保持彈性時,將式(5)和式(8)代入式(1)和式(2),則有

(9)

因此,在這種情況下棘輪邊界為

(10)

(11)

當外纖維屈服時,將式(6)和式(8)代入式(1)和式(2),則有

(12)

其棘輪邊界為

(13)

特別地,若k約等于1,則式(13)可以簡化為

(14)

值得注意的是,當k趨近于1時,式(10)和式(13)與薄壁壓力管道的熱棘輪極限Bree解一致。本節解析解可用于兩端封閉壓力管道的熱棘輪極限設計。

2.2考慮軸向壓力時壓力管道的棘輪極限

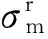
(15)

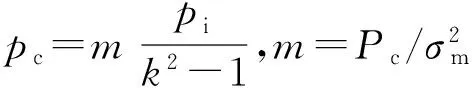
采用Tresca準則進行分析,可分為以下兩種情況:

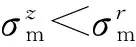
Tresca等效應力為

(16)

當熱循環應力保持彈性,將式(5)和式(16)代入式(1)和式(2)則有

(17)

因此,棘輪邊界可表示為

(18)

當外纖維屈服時,將式(6)和式(16)代入式(1)和式(2),有

(19)

棘輪邊界為

(20)

將式(18)和式(20)等效成Mises等效應力下的棘輪邊界，有

(21)

(22)

由式(21)和式(22)可得到通過不同軸向壓力條件下的棘輪極限,如圖2所示。

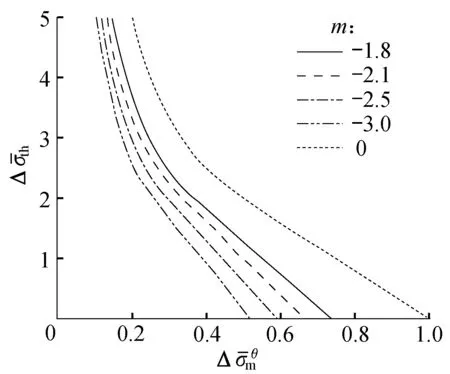
圖2　軸向壓縮對承壓圓筒棘輪極限的影響

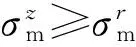
考慮到該情況下計算Tresca等效應力與兩端封閉條件下相同,其棘輪邊界也相同，故該條件下壓力管道的棘輪邊界可用式(10)和式(13)表示。本節解析解可用于考慮軸向壓力下壓力管道的熱棘輪極限設計。

3有限元計算方法及驗證

假定壓力管道的幾何尺寸為:Ri=200 mm,Ro=210 mm,L=1 mm。承受循環熱-機械載荷下壓力管道的應力狀態具有軸對稱性,本文采用Plane 42單元和軸對稱模型進行分析,并沿厚度方向劃分10個網格模型(如圖3),材料參數如表1。

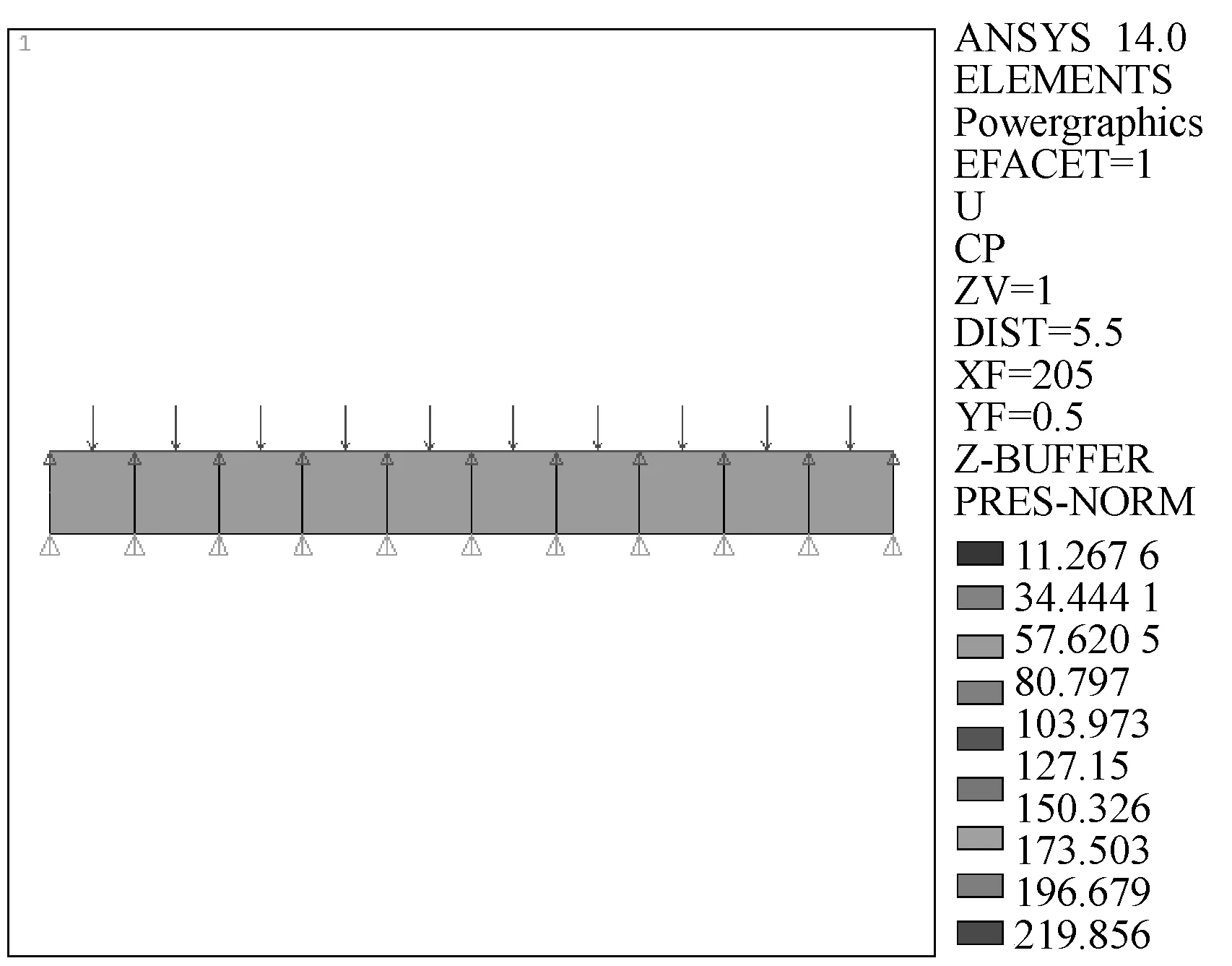
圖3　有限元模型

圖4比較了有限單元法和本文解析解計算的棘輪極限,結果表明了二者吻合良好,最大誤差為3.58%,驗證了本文結果的正確性。

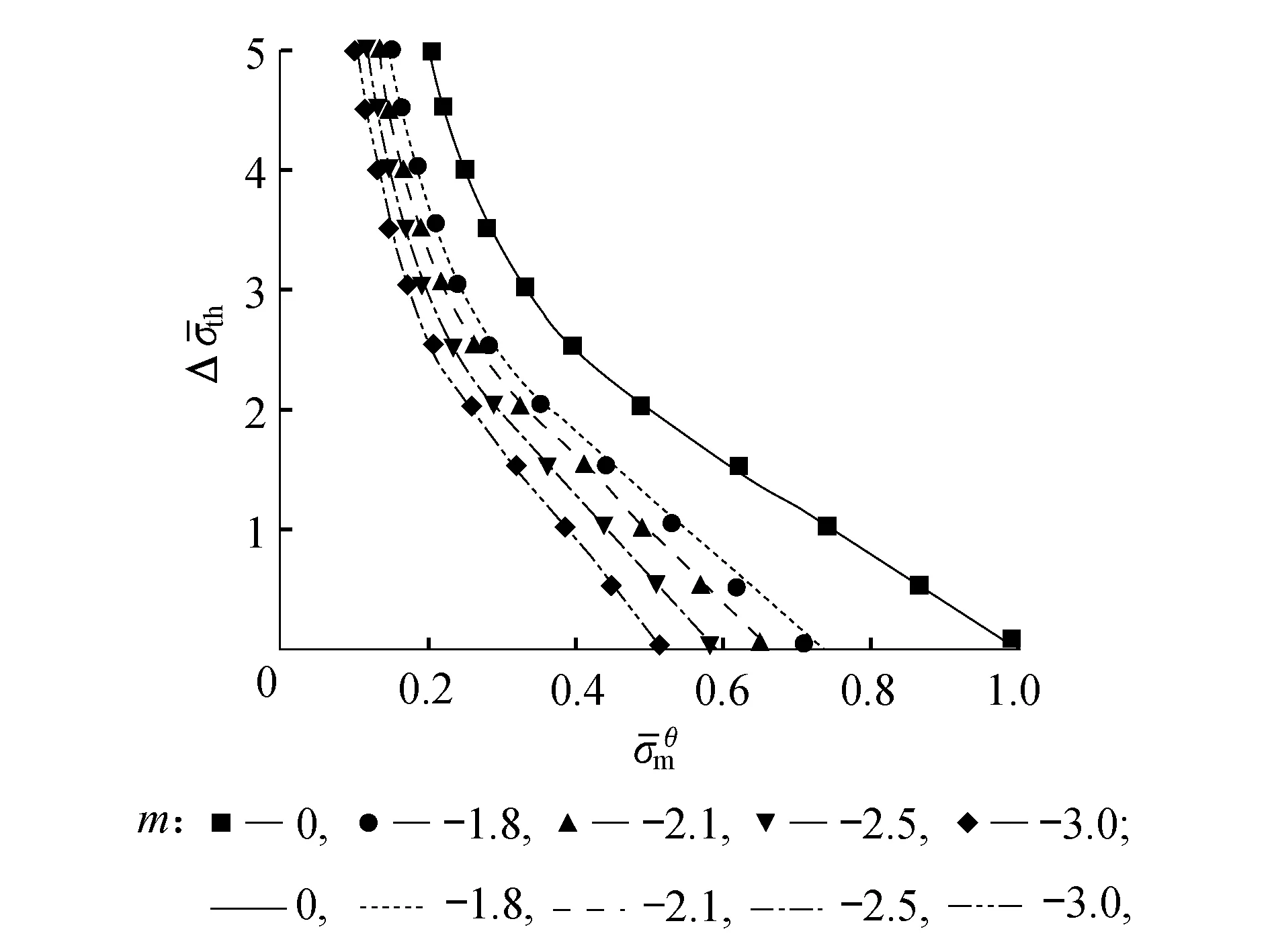
圖4　理論解(線條)與有限元(圖標)結果比較

α/℃νE/MPaσs/MPa1.17×10-50.32.1×105200

4結論

(1)推導了循環熱機械載荷的考慮多軸載荷下壓力管道的熱棘輪極限解析解,進行了有限元驗證,并提出了相應的工程設計方法。

(2)軸向壓應力顯著降低壓力管道的熱棘輪極限,按傳統的Bree理論進行設計時偏于危險,本文為類似復雜載荷下壓力管道的熱棘輪極限設計提供了理論依據。

參考文獻：

[1]BREE J.Elastic-plastic behaviour of thin tubes subjected to internal pressure and intermittent high-heat fluxes with application to fast-nuclear-reactor fuel elements[J].The Journal of Strain Analysis for Engineering Design,1967,2(3):226-238.

[2]BREE J.Plastic deformation of a closed tube due to interaction of pressure stress and cyclic thermal stresses[J].International Journal of Mechanical Science,1989,11(31):865-892.

[3]ZHENG Xiaotao,XUAN Fuzhen.Shakedown of thick cylinders with radial openings under thermo-mechanical loadings[J].Journal of Pressure Vessel Technology,2012,134(1):0112051-0112057.

[4]CHEN Gang,DING Xinwei,HE Kuangguo.Mechanism of biaxial thermal racheting deformation in thin-walled cylindrical shells[J].Engineering Mechanics,1992,9(4):58-69.

[5]REINHARDT W.A non-cyclic method for plastic shakedown analysis[J].Journal of Pressure Vessel Technology,2008,130(3):0312091-0312096.

[6]ADIBI-ASL R,REINHARDT W.Non-cyclic shakedown/ratcheting boundary determination：Part 1.Analytical approach[J].InternationalJournal of Pressure Vessel and Piping,2011,88(8/9):311-320.

[7]ADIBI-ASL R,REINHARDT W.Non-cyclic shakedown/ratcheting boundary determination：Part 2.Numerical implementation[J].International Journal of Pressure Vessel and Piping,2011,88(8/9):321-329.

Ratchet Limit of Pressurized Pipes under Multiaxial Stresses

ZHANG Hong-cai1,3,ZHENG Xiao-tao2,PENG Hong-yu2,XUAN Fu-zhen1,WANG Zheng-dong1

(1.Key Laboratory of Pressurized Systems and Safety,Ministry of Education,East China University ofScience and Technology,Shanghai 200237,China; 2.School of Mechanical and Electrical Engineering,Wuhan Institute of Technology,Wuhan 430205,China; 3.SINOPEC Hubei Chemical Fertilizer Branch,Zhijiang 443200,Hubei，China)

Abstract:Analytical thermal ratchet limit of the pressurized pipes under multiaxial stress condition was deduced based on the non-cyclic method.The effect of axial compressive stress on the ratchet limit was stressed intensively.The corresponding design method was proposed and the closed-form solutions were validated by finite element method.Results revealed that the axial compressive stress will significantly decrease the ratchet limit under multiaxial loading.Moreover,the proposed ratchet limits are in very well agreement with those FEM results.The design method in this paper can be used to evaluate the ratchet limit of the pressurized pipes or other cylindrical structures under similar conditions,which has good engineering significance.

Key words:ratchet limit; pressurized pipes; multiaxial loadings; non-cyclic method

收稿日期：2014-12-10

基金項目：國家自然科學基金 (51305310)

作者簡介：張紅才(1968-),男,高級工程師,從事壓力管道和容器設計及結構完整性方面的研究工作。E-mail:Zhanghc.hbhf@sinopec.com

文章編號：1006-3080(2016)02-0277-04

DOI:10.14135/j.cnki.1006-3080.2016.02.020

中圖分類號：TQ050.2

文獻標志碼：A