自旋波在十字交叉形磁性納米線中的微磁模擬研究

張佳超 王瑞方

摘要：由鐵磁性納米線組成的自旋波導線路將不可避免地發生線路交叉。在交叉區域磁矩呈現明顯不均勻分布，它對自旋波的散射作用可以等效地視為一個自旋波“勢壘”。文章通過微磁模擬方法研究了在不同交變頻率外場激發的自旋波在十字交叉形坡莫合金納米線中的傳播特性，發現勢壘對自旋波傳播的影響與場源頻率有關。

關鍵詞：自旋波；十字交叉形；磁性納米線；勢壘；微磁模擬 文獻標識碼：A

中圖分類號：TQ31 文章編號：1009-2374（2016）17-0013-03 DOI：10.13535/j.cnki.11-4406/n.2016.17.006

1 微磁模擬

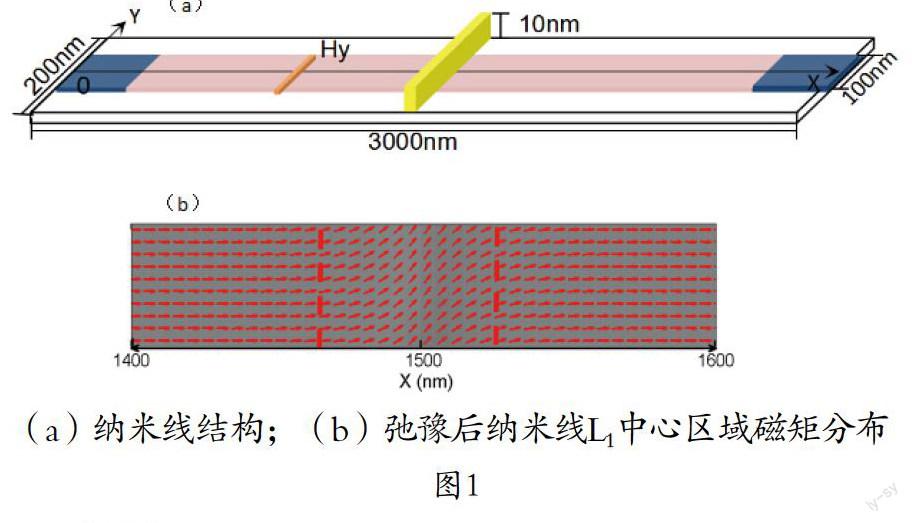
我們設計的十字交叉納米線如圖1（a）所示。底部的坡莫合金納米線（以下簡稱L1）長l1為3000nm，寬w1為100nm，厚度h1為5nm。在x=1500nm處，在L1上疊放一個長度l2=200nm、寬度w2=10nm、厚度h2=10nm的坡莫合金納米線（以下簡稱L2）。兩條納米線夾角為90度。我們設置納米線L1的初始態磁矩沿+x方向，而納米線L2中磁矩沿+y方向。然后樣品在零場條件下弛豫到穩定狀態。達到穩態時，納米線L1中心區域的磁矩分布如圖1（b）所示。在以交叉部位為中心、寬度約200nm范圍內形成了一個磁疇壁（如圖中虛線區域所示）。我們利用微磁模擬軟件LLG Simulator對樣品的磁矩動力學進行數值計算。計算中材料的磁性參數設置為坡莫合金的常用值，即交換作用常數Aes=1.3×1011J/m、飽和磁化強度Ms=800×10-3A/m、吉爾伯特衰減常數α=0.01、磁晶各向異性為零。元胞尺寸為2.5×5×5nm3。在納米線L1兩端250nm區域內，阻尼常數α從0.01逐漸增加到1，以避免自旋波在納米線邊界的反射。

2 結果

為了觀察自旋波在不同頻率下的傳播圖樣，我們在處施加方向的局域振蕩磁場以激發自旋波。其中，激勵場振幅H0=500oe，總模擬時間設定為2ns，激勵場頻率范圍為5～20GHz。當波源頻率高于納米線L1的截止頻率時，自旋波向波源兩邊分別沿+x和-x方向傳播。經過1.9ns的傳播之后，自旋波的波形逐漸達到穩定，如圖2所示：

圖2顯示當自旋波頻率f=5GHz時，自旋波很難在納米線中傳播，磁矩振蕩局限在波源處。當頻率增加至f=8GHz時，自旋波可以在納米線中較為穩定地傳播，并保持較好的波形。自旋波在傳播過程中由于坡莫合金的阻尼作用，使得振幅隨傳輸距離延長而不斷衰減。當自旋波頻率增加至f=12GHz時，穿越勢壘的波形發生了明顯扭曲，自旋波以“之字形”狀態向前傳播。

低頻情況下，波源只激發了基態n=1，自旋波可以在納米線中較為穩定傳播。

而在高頻時，場源除了可以激發基態n=1，還可以激發更高階的對稱模態（如n=3等），這些對稱模態之間會產生自聚焦現象。當自聚焦自旋波到達勢壘時，就會激發偶數模態（如n=2，4等）。所以在勢壘后（即3000nm>X>1500nm）至少存在三種模態，不同模態之間會發生干涉。

3 分析與討論

為了研究這些模態是如何形成的，我們得到了納米線中自旋波的色散關系曲線，如圖3所示。

如圖3（a）所示，在勢壘之前自旋波的振動模式為的奇數模態，截止頻率分別為6.8GHz，15.5GHz，27.5GHz，43.8GHz。而在勢壘之后，出現奇數模態的同時，偶數模態也被激發。圖3（b）中11.1GHz，25.2GHz，35.7GHz分別對應于n=2，4，6模態的截止頻率。

值得注意的是，模態的階數越高即n越大，則對應模態的截止頻率就越高。在低頻段，場源僅激發了n=1模態，自旋波可以在納米線中較為穩定地傳播。中頻段，場源仍然只激發了n=1的模態，但自旋波在勢壘區域受到散射并激發出了n=2模態。因此在勢壘之后的波是對L1中線（y=0）對稱的n=1模態和非對稱的n=2模態的疊加，從而發生自旋波波形扭曲。而在高頻段，更高階的模態被激發，不同模態間相互疊加，形成了干涉圖樣（如圖2中16GHz時的傳播圖樣）。

納米線中，不考慮衰減，第n階模態的磁矩振幅的空間分布可以表示為：

式中：是納米線的有效寬度；表示波源激發頻率；為該頻率下激發的n階模態的自旋波軸向傳播波矢；為激發波源的初始相位；是相對勵磁效率。取在一個周期內取平均值，可以得到第n個模態的強度分布。以f=16GHz，為例，得到模態n=1和n=3的強度分布，如圖4（a）、（b）所示。不同模態間會疊加，振幅的空間分布可以表述為：

不考慮波強的衰減，從理論上得到的波強分布如圖4（c）所示，而微磁模擬得到的納米線波強分布如圖4（d）所示，可以看到兩者大致吻合。這說明波源激發的波包含兩種模態n=1和n=3。同樣f=12GHz時，當自旋波通過勢壘可以激發n=2的非對稱模態。對比微磁模擬結果，得到如圖4（e）、（f），兩者大致也吻合。這恰恰也說明，在圖2中看到的中高頻段波形的扭曲，是由于對稱模態和非對稱模態之間的疊加，從而使自旋波以“之字形”狀向前傳播。

另外，圖2顯示當外加場源的頻率不同時，經過勢壘之后的自旋波的振幅也發生了不同的變化。當自旋波傳播到勢壘區域時，一部分波會被勢壘所反射；另一部分自旋波則會發生透射，繼續向+x方向傳播。不同頻率下，自旋波穿透勢壘的能力不同。如圖5所示為透射系數和反射系數與頻率f之間的關系。反射系數和透射系數可通過下式得到：

式中：MI為自旋波在穿過勢壘前的入射振幅；MT為自旋波穿過勢壘時的透射振幅；MR為被勢壘反射的自旋波振幅。計算多個時刻的反射系數和透射系數，并取平均值得到和。由圖5所知，在f=12GHz時透射系數最大，接近等于1；在f=17GHz時，透射系數最小。從計算結果看，。

同時我們發現磁疇壁的寬度隨著頻率也是振蕩變化的。磁疇壁的寬度可以表示為：

式中：L1、L2分別表示磁疇壁左右邊界所在的位置。

我們設定Mx=0.95的位置為磁疇壁邊界。在特定頻率的交變外場的作用下，一開始，自旋波還未傳播到勢壘區域，所以疇壁寬度保持不變。當自旋波傳播到勢壘區域之后，疇壁的邊界位置隨之發生振蕩，因此根據式（4）疇壁寬度也隨時間發生振蕩。磁疇壁存在兩種不同的振蕩模式。在f=11GHz，疇壁左右邊界以相同相位振動；而在場源頻率在17GHz時，左右邊界呈反相振動。磁疇壁的兩種振蕩模式可能會影響自旋波在勢壘處的反射系數和透射系數，但這背后的物理機制尚待進一步的研究。并且隨著外加場源頻率的增加，疇壁寬度振幅逐漸減小。這是因為隨著頻率增大，磁振子的能量越大，從而勢壘對自旋波的阻礙作用相對較小而造成的。

4 結語

我們采用微磁模擬方法研究了自旋波在十字形坡莫合金納米線中的傳播特性。低頻波源僅激發出n=1的模態，自旋波可以在納米線以穩定波形傳播。高頻自旋波在受到十字交叉區域的勢壘散射作用后，激發出偶數模態使得透射出去的自旋波以“之字形”傳播。我們還研究了不同頻率下自旋波在勢壘處的反射系數與透射系數，發現在f=12GHz時透射系數最大，而f=17GHz時透射系數最小。在自旋波作用下疇壁區域產生兩種振蕩模式，一種為左右邊界同相振動，另一種為左右邊界反相振動。自旋波透射系數與頻率的關系以及它和疇壁振動模式間的關系的物理機制尚待進一步研究。

參考文獻

[1] V.V.Kruglyak，et al.J.Phys.D：Appl.Phys.43，264001，2010.

[2] A.Khitun，et al.J.Phys.D：Appl.Phys.43，264005，2010.

[3] Hertel，R.，Wulfhekel，W.&Kirschner，J.Domain-wall induced phase shifts in spin waves.Phys.Rev.Lett.93，257202，2004.

[4] Schneider，T，et al.Realization of spin-wave logic gates.Appl.Phys.Lett.92，022505，2008.

[5] International Technology Roadmap for Semiconductors（ITRS）2009 edition.Emerging Research Devices，2009.

作者簡介：張佳超（1990-），女，浙江紹興人，廈門大學物理與機電工程學院在讀碩士，研究方向：低維磁性納米材料。

（責任編輯：黃銀芳）