T.Figiel定理及其應(yīng)用

馬玉梅

(大連民族大學(xué) 理學(xué)院，遼寧 大連116605)

?

T.Figiel定理及其應(yīng)用

馬玉梅

(大連民族大學(xué) 理學(xué)院，遼寧 大連116605)

摘要：等距延拓問(wèn)題是幾何和泛函分析領(lǐng)域的重要課題。在Mazur-Ulam定理基礎(chǔ)上，給出了T.Figiel定理的一個(gè)等價(jià)命題以及它在等距逼近問(wèn)題中的應(yīng)用。

關(guān)鍵詞：等距；等距逼近；連通集

等距算子及其延拓問(wèn)題的研究在幾何泛函分析領(lǐng)域占有重要位置。80多年來(lái)一直是研究的熱點(diǎn)問(wèn)題[1-13]。 1932年Mazur-Ulam定理給出兩個(gè)賦范空間之間的滿等距映射必為仿射變換。1968年T.Figiel考慮將Mazur-Ulam定理中的“滿映射”改為“嵌入映射”給出了一個(gè)一般性的著名定理[1]：

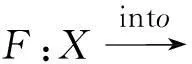
為了證明T.Figiel定理，該作者首先給出了以下兩個(gè)引理：

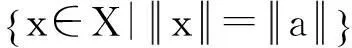
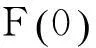
本文推廣了引理1，同時(shí)也給出了一個(gè)與T.Figiel定理等價(jià)的命題。

此外，本文還考慮了非線性Lipschitzε-等距逼近問(wèn)題：映射T:E→F為L(zhǎng)ipschitzε-等距，如果對(duì)任何x,y∈E，有

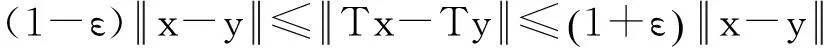
對(duì)于這類(lèi)ε-等距映射T是否存在等距逼近一直是許多數(shù)學(xué)家從事的課題[2-10]。

1T.Figiel引理的推廣

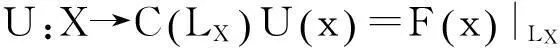
證明首先，定理2?T.Figiel定理顯然成立。

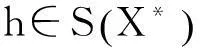
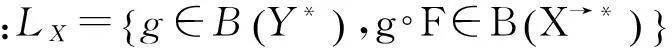
再令：

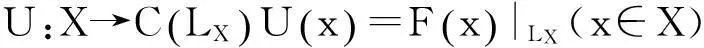
2T.Figiel引理的應(yīng)用

作為T(mén).Figiel定理的一個(gè)應(yīng)用，下面考慮Lipschitzε-等距逼近問(wèn)題，這里的證明方法是通過(guò)改進(jìn)P.M.Gruber[11]的方法(絕對(duì)誤差的ε-等距逼近問(wèn)題的證明過(guò)程中的方法)得到的。

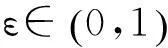
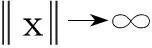
(2)T(0)=U(0)=0，

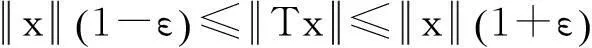
(1)

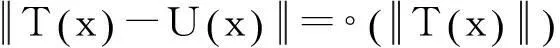
(2)

下面證明

(3)

事實(shí)上，由于T是滿射，?y∈Y，?x∈X，使得Tx=y，從而對(duì)于?λ>0,?xλ∈X使得

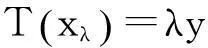
(4)

根據(jù)式(1)得到

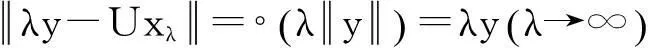
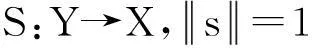
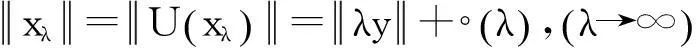
(5)

由于

(6)

于是由式(4)(5)得到

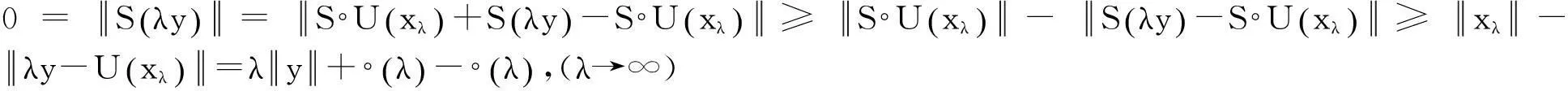
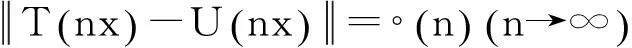
當(dāng)反過(guò)來(lái)考慮上面的命題時(shí)可以得到當(dāng)空間為有限維時(shí)的以下定理。

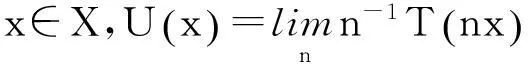
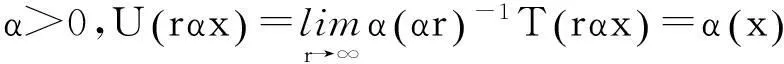
下面證明

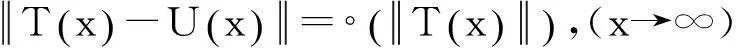
(7)

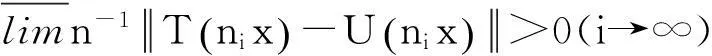
(8)

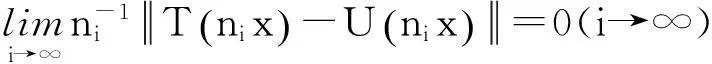
此式與式(8)矛盾。這樣完成了命題的證明。

注：從這個(gè)命題可以發(fā)現(xiàn)這一結(jié)果不十分理想，沒(méi)有得到U(x)為等距映射。

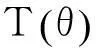
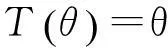
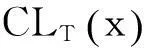
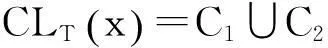
下面證明存在N，使得當(dāng)r≥N時(shí)，

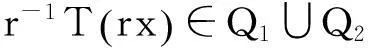
(9)

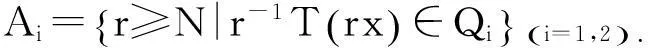
參考文獻(xiàn)：

[1]FIGIELT.Onnonlinearisometricembeddingsofnormedlinearspaces,[J].BullAcadPolonSciserSciMathAstronomphys,1968, 16: 185-188.

[2]LIXinbaoCHENGLixin,CHENGQingjin,etal.Onuniversallyleft-stabilityof-isometry[J].ActaMathematica,SinicaEnglishSeries, 2013, 29(11):2037-2046.

[3]HYERSDH,ULAMSM.Onapproximateisometries[J].BullAmerMathSoc, 1945, 51:288-292.

[4]GERIVTZJ.StabilityofisometriesonBanachspaces[J].ProcAmerMathSoc, 1983, 89(4):633-636.

[5]OMLADICM,SEMRLP.Onnonlinearperturbationsofisometrles[J].MathAnn1995,303:617-628.

[6]LOVBLOMGM.Isometriesandalmostisometriesbetweenspacesofcontinuousfunctions[J].IsraelJournalMathematics,1986,56(2):143-159.

[8]DINGGuanggui.IsometrieandalmostisometrieoperatorsofB(L1-L∞) [J].ActaMathSinica, 1985,1(2):126-140.

[9] 定光桂.關(guān)于幾乎等距嵌入的一個(gè)注記[J]. 數(shù)學(xué)學(xué)報(bào), 2001, 44(2): 273-279.

[10] 定光桂. 等距算子的延拓、逼近及相關(guān)問(wèn)題 [J]. 數(shù)學(xué)進(jìn)展, 2003, 5: 529-536.

[11]BOURGINDG.Approximateisometries[J].BullAmerMathSoc, 1946(52)：704-714.

[12]MAYumei.TheAleksandrovproblemandTheMazue-Ulamtheoremonlinearn-normedspace[J].BulletinoftheKoreanMathematicalSociety, 2013 (50)：1631-1637.

[13]MAYumei.Isometryonlinearn-normedspaces[J].AnnalesAcademiScientiarumFennicMathematica,2014, 39: 973-981.

(責(zé)任編輯鄒永紅)

T.Figiel′s Theorem and Its Application

MA Yu-mei

(School of Science, Dalian Minzu University, Dalian Liaoning 116605, China)

Abstract:The extension problem on isometry is an important issue in the field of geometry and functional analysis. Base on Mazur-Ulam theorem, we give an equavilent proposition of T.Figiel' s theorem and its applications on isometric approximate problems.

Key words:isometry；isomatric approximation；connected set

收稿日期：2015-06-30；最后修回日期：2106-01-05

基金項(xiàng)目：中央高校基本科研業(yè)務(wù)費(fèi)專(zhuān)項(xiàng)資金資助項(xiàng)目(DC201502050301)。

作者簡(jiǎn)介：馬玉梅(1962-)， 女，遼寧海城人，教授，博士，主要從事泛函分析相關(guān)問(wèn)題研究。

文章編號(hào)：2096-1383(2016)03-0224-02

中圖分類(lèi)號(hào)：O177.3

文獻(xiàn)標(biāo)志碼：A