半線性橢圓最優(yōu)控制問題插值系數(shù)混合有限元解的先驗(yàn)誤差估計(jì)

曹龍舟，魯祖亮，2，李林

（1.重慶三峽學(xué)院非線性科學(xué)與系統(tǒng)重點(diǎn)實(shí)驗(yàn)室，重慶404100；2.天津財(cái)經(jīng)大學(xué)數(shù)學(xué)與經(jīng)濟(jì)研究中心，天津300222）

半線性橢圓最優(yōu)控制問題插值系數(shù)混合有限元解的先驗(yàn)誤差估計(jì)

曹龍舟1，魯祖亮1，2，李林1

（1.重慶三峽學(xué)院非線性科學(xué)與系統(tǒng)重點(diǎn)實(shí)驗(yàn)室，重慶404100；2.天津財(cái)經(jīng)大學(xué)數(shù)學(xué)與經(jīng)濟(jì)研究中心，天津300222）

利用插值系數(shù)混合有限元方法求解半線性最優(yōu)控制問題，采用插值系數(shù)的思想去處理方程中的非線性項(xiàng)，建立了半線性橢圓最優(yōu)控制問題插值系數(shù)混合有限元的離散格式，將狀態(tài)方程和對(duì)偶狀態(tài)方程利用低階的Raviart-Thomas混合有限元空間離散，控制變量利用分片常函數(shù)逼近，最后獲得狀態(tài)變量和控制變量的L2范數(shù)和H（div）范數(shù)的最優(yōu)階先驗(yàn)誤差估計(jì).

半線性橢圓；最優(yōu)控制問題；插值系數(shù)混合有限元解；先驗(yàn)誤差估計(jì)

1 引言

最優(yōu)控制問題的數(shù)值模擬是科學(xué)與工程計(jì)算中一個(gè)重要的研究領(lǐng)域.最早是Falk[1]和Geveci[2]研究了橢圓最優(yōu)控制問題的有限元方法.接下來有很多專家學(xué)者研究了最優(yōu)控制問題的各種有限元離散格式.插值系數(shù)混合有限元方法是經(jīng)濟(jì)有效的方法，Zlamal[3]最先分析半線性拋物問題插值系數(shù)混合有限元方法.接著，Larsson，Tomee[4]研究了非線性熱方程的半離散插值系數(shù)混合有限元方法.國(guó)內(nèi)學(xué)者陳艷萍和熊之光[5，6]研究了半線性橢圓問題有限元的超收斂.本文，我們主要研究一般的半線性橢圓最優(yōu)控制問題插值系數(shù)混合有限元方法，獲得狀態(tài)和控制變量的L2范數(shù)和H（div）范數(shù)的先驗(yàn)誤差估計(jì).

我們考慮如下半線性橢圓問題：

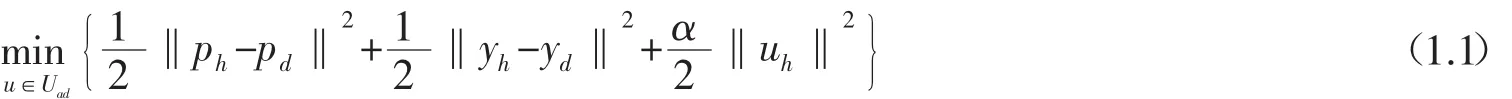
其狀態(tài)方程為

邊值條件為

這里Ω是一個(gè)矩形區(qū)域，pd和yd是目標(biāo)函數(shù)，p和y是狀態(tài)變量，u是控制變量，α是正常數(shù).假設(shè)f∈L2（Ω），B是L2（Ω）→L2（Ω）上的連續(xù)線性算子.控制變量的約束集Uad定義如下：

下面我們給出系數(shù)矩陣A（x）和函數(shù)φ的假設(shè).

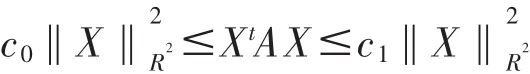
2 插值系數(shù)混合有限元方法

這一節(jié)，通過插值系數(shù)算子Ih代替非線性項(xiàng)φ（yh），利用插值系數(shù)混合有限元方法求解半線性橢圓最優(yōu)控制問題.現(xiàn)在我們討論最優(yōu)控制問題（1.1）-（1.4）的插值系數(shù)混合有限元離散格式.令W=L2（Ω），

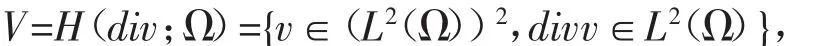
其范數(shù)為：

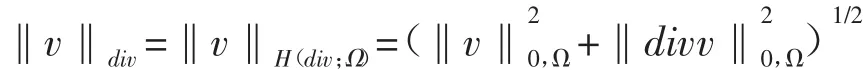
這時(shí)最優(yōu)控制問題（1.1）-（1.4）的弱形式為：尋找（p，y，u）∈V×W×U使得

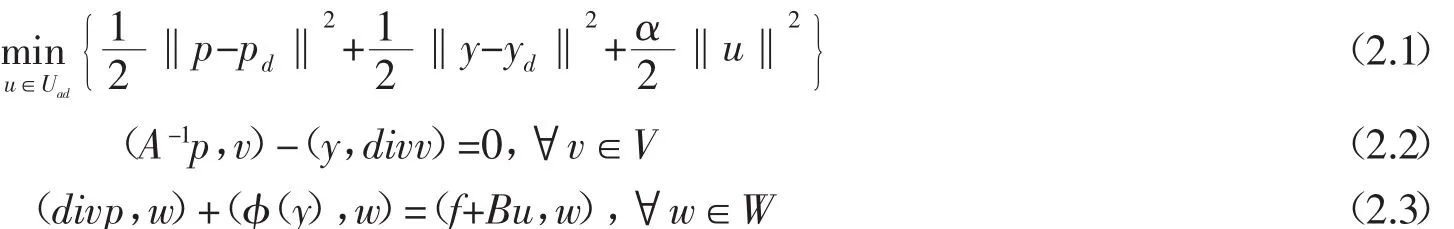
眾所周知，問題（2.1）-（2.3）至少有一個(gè)解（p，y，u），而且（p，y，u）∈V×W×U是問題（2.1）-（2.3）的解的充分必要條件是存在（q，z）∈V×W使得（p，y，q，z，u）滿足如下的最優(yōu)性條件：

這里B*是B的共軛算子.

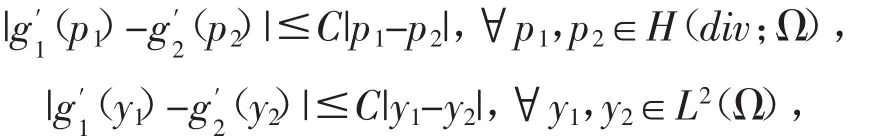
且存在一個(gè)正常數(shù)c，使得

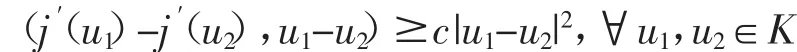
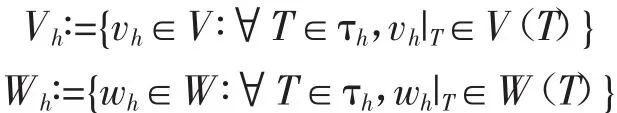
為了逼近控制變量，我們定義Uad為分片常函數(shù)有限元子空間：

問題（2.1）-（2.3）的混合有限元逼近形式為：尋找（ph，yh，uh）∈Vh×Wh×Uh使得

定義插值算子Ih：C（Ω）→Wh使得

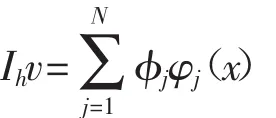
并且有如下插值誤差估計(jì)[4]：當(dāng)0≤m≤r，1≤p≤∞時(shí)，有

這里對(duì)于所有的T∈τh有v∈C（Ω）∩Wr，p（τh）.在式子（2.11）里用Ihφ（yh）代替φ（yh），則最優(yōu)控制問題（2.9）-（2.11）至少存在一個(gè)解（ph，yh，uh），并且如果（ph，yh，uh）是（2.9）-（2.11）的解，那么總存在一個(gè)對(duì)偶狀態(tài)變量（qh，zh）∈Vh×Wh使得（ph，yh，qh，zh，uh）滿足如下最優(yōu)性條件：

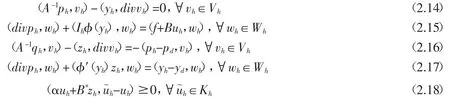
令Qh∶U→Uh是一個(gè)標(biāo)準(zhǔn)L2（Ω）-正交投影，且滿足對(duì)于任意的u~∈U，有

對(duì)于φ∈Wh，我們可以寫成

這里

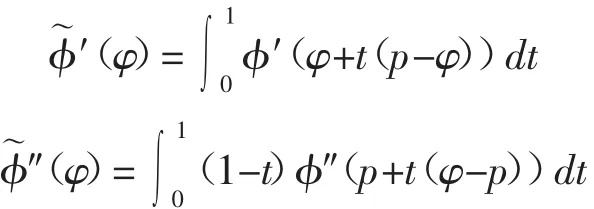
是Ω上的有界函數(shù)[10].

3 先驗(yàn)誤差估計(jì)

這一節(jié)，我們將討論半線性橢圓最優(yōu)控制問題插值系數(shù)混合有限元逼近解的先驗(yàn)誤差估計(jì).首先引入中間變量，對(duì)于任意控制函數(shù)u~∈Uad，定義狀態(tài)方程的離散解（ph（u~），yh（u~），qh（u~），zh（u~））使得

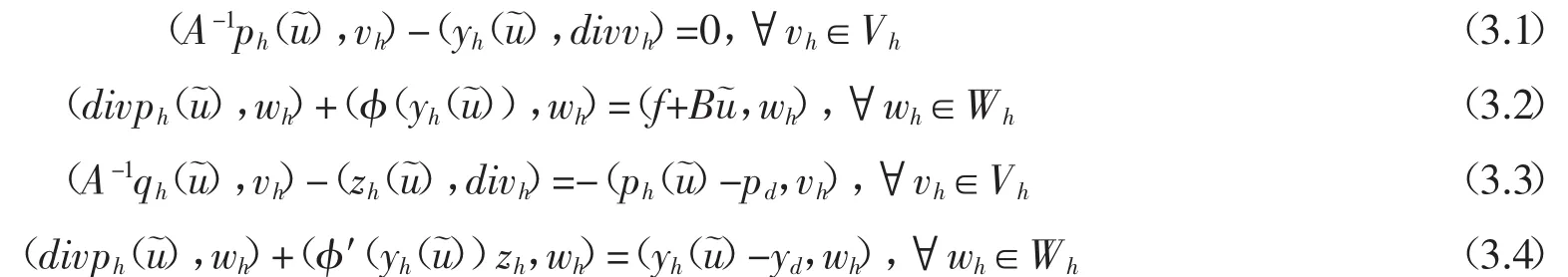
定義中間誤差：

為了估計(jì)中間變量的誤差，利用公式（2.21），結(jié)合（2.4）-（2.7）和（3.1）-（3.4），并選擇u~=u得到：

這里vh∈Vh，wh∈Wh.

類似于文獻(xiàn)[11]的證明思路，結(jié)合（3.7）-（3.10），我們可以得到如下引理.

引理3.1假設(shè)（A1）-（A2）均滿足，則存在一個(gè)與h無關(guān)的正常數(shù)C使得

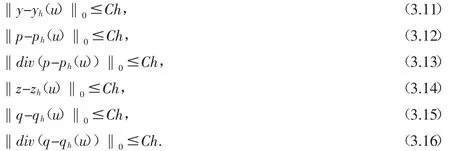
引入中間誤差變量，我們能夠?qū)⒄`差分解為：

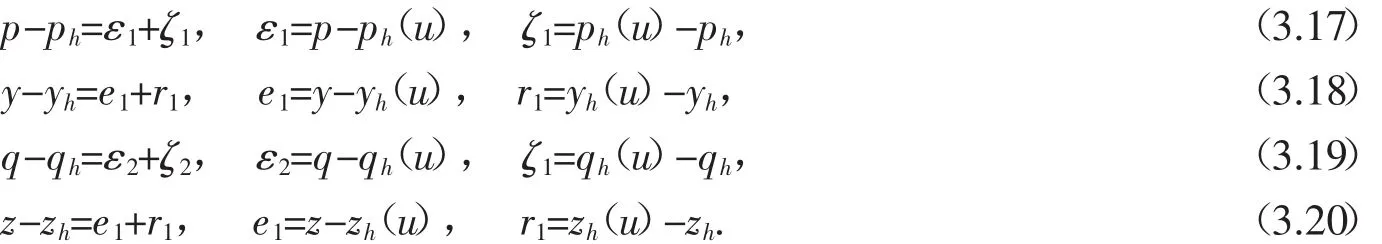
利用混合有限元方法的穩(wěn)定性結(jié)論，我們可以得到如下結(jié)果.

定理3.1假設(shè)（A1）-（A2）均滿足，則存在一個(gè)與無關(guān)的正常數(shù)使得

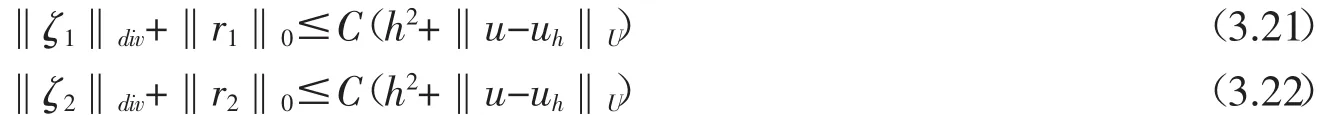
證明：根據(jù)（2.14）-（2.17），（3.1）-（3.4）和（2.21），我們有如下誤差方程：

令

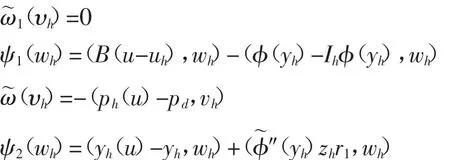
對(duì)于插值算子Ih通過使用插值誤差估計(jì)（2.13），我們有

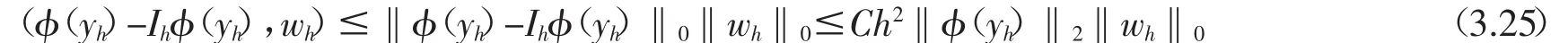
利用（3.25）和連續(xù)的線性算子B的性質(zhì)，有

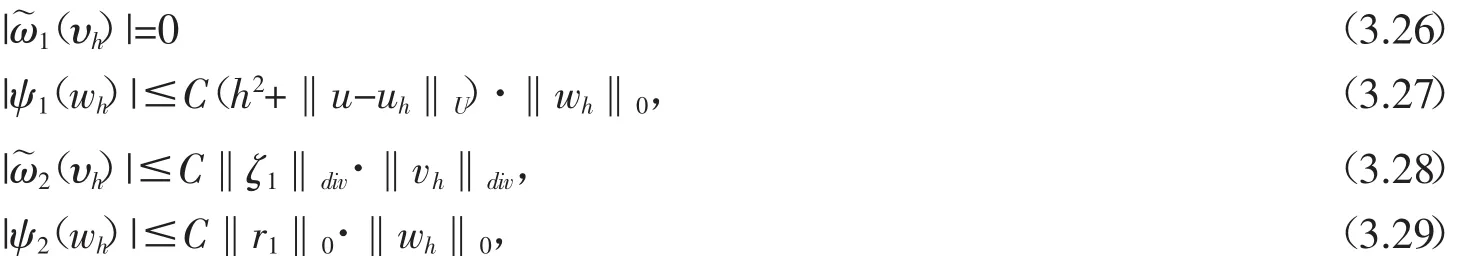
從（3.23）和（3.26）-（3.27）可以得到

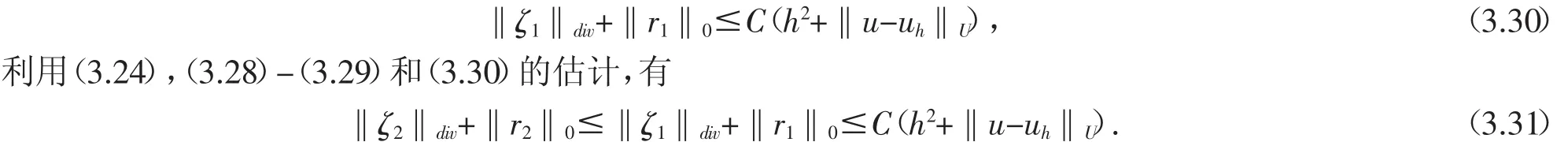
證明完畢.

令（p（u），y（u））和（ph（u），yh（u））分別為（2.2）-（2.3）和（3.1）-（3.2）的解，再令J（·）∶U→R2是一個(gè)G微分凸泛函的近似解u滿足如下形式：

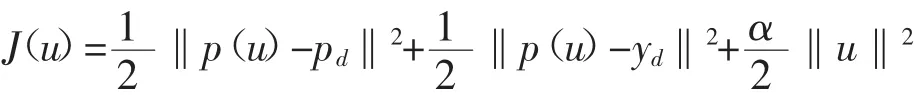
假設(shè)有如下凸泛函序列Jh∶U→R2滿足

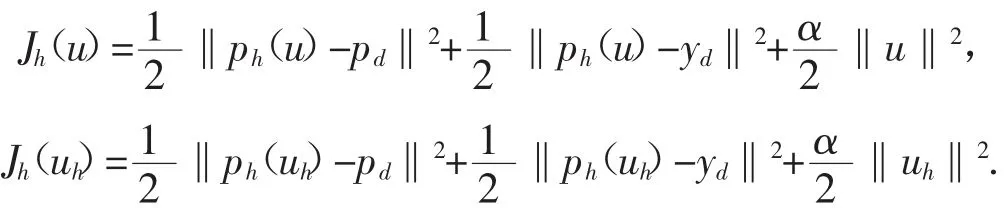
容易得到

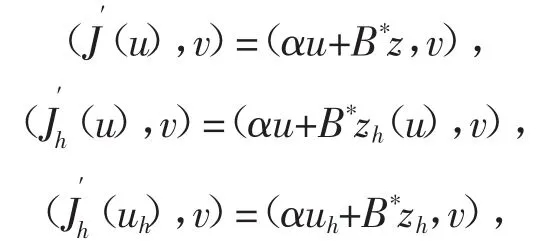
接下來，我們來估計(jì)‖u-uh‖.假設(shè)目標(biāo)函數(shù)J在解u的某個(gè)小鄰域內(nèi)是嚴(yán)格一致凸泛函，即對(duì)于解u存在一個(gè)小鄰域使得J在該鄰域上是凸函數(shù)，也就是說存在一個(gè)獨(dú)立于h的正常數(shù)c使得

定理3.2假設(shè)（A1）-（A2）都滿足，令（p，y，q，z，u）∈（V×W）2×U以及（ph，yh，qh，zh，uh）∈（Vh×Wh）2×Uh分別為（2.14）-（2.18）和（2.14）-（2.18）的解，假設(shè)（αu+B*z）∈H1（Ω），這時(shí)有

和

注意到在（3.37）中Qhu-uh=Qhu-u+u-uh，結(jié)合（3.36）-（3.37），有

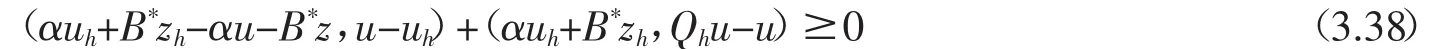
由（3.38）可以得到

應(yīng)用（3.32）和（3.39），有

現(xiàn)在我們估計(jì)（3.40）的右端項(xiàng)，由算子B的連續(xù)性和定義（3.1）可以得到

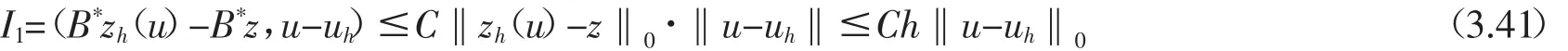
因?yàn)閖′是局部Lipschitz連續(xù)，利用δ-Caunchy不等式和（2.20）中投影算子Qh的逼近性質(zhì)，容易得到

對(duì)于任意的δ＞0成立.由（2.20），（3.11）和算子B的連續(xù)性，我們有

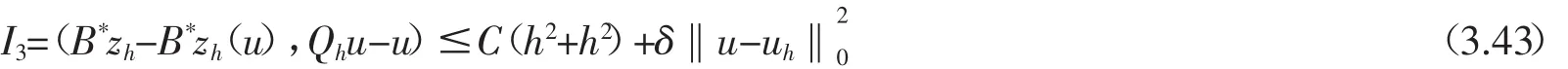
和

然后利用定理3.2的假設(shè)和（2.20）的逼近性質(zhì)，有

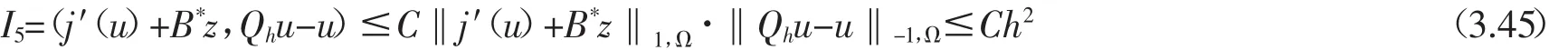
利用（3.41）-（3.45）和（3.40），可以證明（3.33）.再結(jié)合引理3.1和定理3.1，我們得到（3.34）-（3.35）.

[1]F.S.Falk.Approximation ofa class ofoptimal control problems with order ofconvergence estimates[J].J.Math.Anal.Appl.，44（1973）：28-47.

[2]T.Geveci.On the approximation ofthe solution ofan optimal control problemgoverned byan elliptic equation[J].R.A.I.R.O.Numer.Anal.，1979（13）：313-328.

[3]M.Zlamal.Afinite element solution ofthe nonlinear heat equation[J].R.A.I.R.O.Numer.Anal.，1980（14）：203-216.

[4]S.Larsson，V.Tomee.Interpolation ofcoefficients and transformation ofdependent variable in Element methods for the nonlinear heat equation [J].Math.Methods Appl.Sci.，1989（11）：105-124.

[5]Z.Xiong，Y.Chen.Arectangular finite volume element for a semilinear elliptic equation[J].J.Sci.comp.，2008（36）：177-179.

[6]Z.Xiong，Y.Chen.Finite volume element method with interpolation cofficients for two-point boundaryvalue problemofsemilinear differential equation[J].Comput.MethodsAppl.Mech.Engrg.，2007（196）：3798-3804.

[7]張宏偉，劉衍瓊.對(duì)流占優(yōu)擴(kuò)散微分方程的最小二乘特性有限元方法[J].懷化學(xué)院學(xué)報(bào)，2008，27（11）：1-4.

[8]張宏偉，何敬偉.一類對(duì)流擴(kuò)散方程的耦合解法[J].懷化學(xué)院學(xué)報(bào)，2010，29（2）：1-5.

[9]P.A.Raviart，J.M.Thomas.Amixed finite element method for 2nd order elliptic problems，Math.Aspects ofthe Finite Elment method[J]. Lecture Notes in Math，2012（2）：292-315.

[10]Y.Kwon，F(xiàn).A.Milner.-error estimates for mixed methods for semilinear second-order elliptic equation[J].SIAMJ.Control Numer.Anal.，1988（25）：46-53.

[11]Z.Lu，Y.Chen.-error estimates oftriangular mixed finite element methods for optimal control problemgovern bysemilinear elliptic equation [J].Numer.Anal.Appl.，2009（12）：77-86.

[12]F.Brezzi，M.Fortin.Mixed and hybrid finite element methods[J].Springer，Berlin，1991.

Interpolation Coefficients Mixed Finite Element Solutions For Semilinear Elliptic Optimal Control Problems Priori Error Estimates

CAO Long-zhou1，LU Zu-liang1，2，LI Lin1
（1.Key Laboratory for Nonlinear Science and System Structure，Chongqing Three Gorges University，Chongqing 404000；2.Research Center for Mathematics and Economics，Tianjin University of Finance and Economics，Tianjin 300222）

In this paper，the authors extend the excellent idea of interpolation coefficients for semilinear optimal control problems to the mixed finite element methods.By using the interpolation coefficients thought to process the nonlinear term of equations，we present the mixed finite element approximation with interpolation coefficients for general optimal control problems governed by semilinear elliptic equations.The state and the co-state are discretized by the lowest order Raviart-Thomas mixed finite element space and the control is discretized by piecewise constant elements.We derive a priori error estimates in L2norm and H（div）norm for the coupled state and control variables with optimal convergence order h2.

semilinear elliptic；optimal control problems；interpolation coefficients mixed finite element solutions；priori error estimates

O241.82

A

1671－9743（2016）11－0021－06

2016-06-18

國(guó)家自然科學(xué)基金（11201510，11171251）；中國(guó)博士后科學(xué)基金（2015M580197）；重慶市科委項(xiàng)目（cstc 2015 jcyjA20001）；教育部春暉計(jì)劃（Z2015139）.

曹龍舟，1994年生，男，重慶開縣人，碩士研究生，研究方向：偏微分方程數(shù)值解；魯祖亮，1980年生，男，湖南常德人，教授，博士，碩士生導(dǎo)師，研究方向：偏微分方程數(shù)值解；李林，1992年生，男，重慶萬州人，碩士研究生，研究方向：偏微分方程數(shù)值解.