多元多項式的最大公因式

劉金旺，何秀秀

（湖南科技大學數學與計算科學學院，湖南湘潭411201）

多元多項式的最大公因式

劉金旺，何秀秀

（湖南科技大學數學與計算科學學院，湖南湘潭411201）

主要討論多項式環上兩個多元多項式的最大公因式的求解問題，通過探討理想的交、最大公因式和最小公倍式三者之間的關系，采用Gr?bner基的理論和方法，總結出理想的交與最小公倍式之間的關系，進而給出求解最大公因式的有效方法與算法，最后給出具體實例說明該方法的可行性.

多元多項式；多元多項式環；最大公因式

1 引言

多項式理論是代數學的重要內容，尋找兩個多項式的最大公因式問題是多項式理論中非常困難的問題.求解兩個一元多項式的最大公因式一般是先把兩個多項式分解成一些不可約多項式的乘積，我們知道分解因式特別困難.目前，已有不少學者對其進行了較多的研究，關于一元多項式的最大公因式問題得到了一些較好的結果，常用的方法有毆幾里德算法，系數矩陣的初等變換法等，都從不同的角度對其進行了研究.但是，對于多元多項式的最大公因式問題并沒有得到比較好的解決，而且有關這方面的理論也比較少.其中，文獻[2]討論了兩個二元多項式的最大公因式的存在性，并且給出了相應的證明，也得出一系列性質.文獻[3]對兩個二元多項式的最小公倍式進行了探討，也得出相應的結論.文獻[5]討論了多元多項式可約性的相關性質.

本文主要致力于研究兩個多元多項式最大公因式問題，通過引進Gr?bner基的理論與方法，探討理想、最小公倍式、最大公因式三者之間的關系，給出尋找最大公因式的有效方法和算法.

本文主要是在多元多項式環k[x1，…，xn]上進行探討，下面給出相關的定義：

定義1[1]設f（x1，…，xn），g（x1，…，xn），h（x1，…，xn）∈k[x1，…，xn]，如果h（x1，…，xn）滿足：

（1）h（x1，…，xn）整除f（x1，…，xn），g（x1，…，xn）；

（2）如果p（x1，…，xn）是f（x1，…，xn），g（x1，…，xn）的公因式，則p（x1，…，xn）整除h（x1，…，xn）.則稱h（x1，…，xn）是f（x1，…，xn），g（x1，…，xn）的最大公因式，記作GCD（f（x1，…，xn），g（x1，…，xn））.

定義2[1]設f（x1，…，xn），g（x1，…，xn），h（x1，…，xn）∈k[x1，…，xn]，若h（x1，…，xn）∈k[x1，…，xn]滿足：

（1）f（x1，…，xn），g（x1，…，xn）整除h（x1，…，xn）；

（2）h（x1，…，xn）整除f（x1，…，xn），g（x1，…，xn）的每個公倍式.則稱h（x1，…，xn）是f（x1，…，xn），g（x1，…，xn），的最小公倍式，記作LCM（f（x1，…，xn），g（x1，…，xn））.

定義3[1]設其中I是有限集，令表示f（x1，…，xn）中出現的所有單項式的集合，令中所有項的集合.假設≤是T上的單項式序，對于非零的多項式f∈k[x1，…，xn]，稱（T（f），≤）中的最大項為f的首項，用HT（f）表示；稱（M（f），≤）中的最大項為f的首單項式，用HM（f）表示；首單項式HM（f）的系數稱為首系數，用HC（f）表示.顯然有HM（f）=HC（f）HT（f）.

定義4[1]對于固定的單項式序，非零理想I?k[x1，…，xn]的有限子集G={f1，f2，…，ft）稱為I的Gr?bner基，如果他們滿足

定義5[1]設G是理想I的Gr?bner基，如果G滿足下列條件：

（1）?f∈G，HC（f）=1；

（2）對任意f∈G，f模G{f}是不可約的.

則稱G是I的既約Gr?bner基.

定義6[1]設J=＜f1，f2，…，fs＞?F[x1，…，xn]，則第m個消元理想Jm是F[xm+1，…，xn]中的理想，記為Jm=J∩F [xm+1，…，xn]，消元理想Jm包含了方程組f1=f2=…=fs=0消去變元x1，…，xk后所能推出的所有多項式.

定義7[1]對于i≠j有如下記法：

2 主要結論

首先給出相關引理以及計算理想的交的基本算法：

引理1[1]設I1，I2，…，Im是多項式環k[x1，…，xn]上的理想，令y1，…，ym是一組新的變元，在多項式環k[y1，y2，…，ym，x1，x2，…，xn]上定義理想

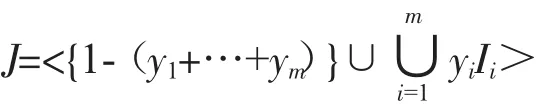
其中k[y1，y2，…，ym，x1，x2，…，xn]上的單項式序為字典序，滿足

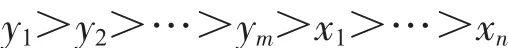
引理2[1]設J?F[x1，…，xn]是一個理想，設G是理想J的Gr?bner基，單項式序是字典序，并且滿足x1＞x2＞…＞xn，則對于每一個0≤k≤n，集合Gk=G∩F[xk+1，…，xn]是第k個消元理想Jk的Gr?bner基.

關于計算兩個理想的交的算法如下：

輸入：理想I，J∈k[x1，x2，…，xn]且I=＜f（x1，x2，…，xn）＞，J=＜g（x1，x2，…，xn）＞.

輸出：I∩J.

第一步：分別求出理想I和J的Gr?bner基：{f（x1，x2，…，xn）}，{g（x1，x2，…，xn）}；

第二步：引入新變元y1，y2，并在k[y1，y2，x1，…，xn]上構造新的理想

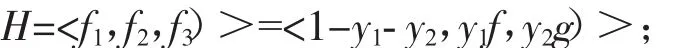
第三步：利用Gr?bner基的算法[4]求的Gr?bner基，具體操作如下：令G=H；B={（i，j）｜1≤i＜j≤13}；t=3；如果B≠0，則執行下列語句：取（i，j）∈B，如果LCM（HT（fi），HT（fj））≠HT（fi）· HT（fj）且Crit（fi，fj，B）=false，則h0=S（fi，fj）G；如果h0≠0；則t=t+1；ft=h0；G=G∪{ft}；B=B∪{（i，j）｜1≤i≤t-1}；B=B-{（i，j）}；結束（其中Crit（fi，fj，B）=true當且僅當存在k?{i，j}，使得[i，k]，[j，k]?B且HT（fk）|LCM（HT（fi），HT（fj））），則最終G為所求的Gr?bner基.

第四步：通過上述辦法所求得的Gr?bner基G，則G∩k[x1，…，xn]為I∩J的Gr?bner基.

定理1設f（x1，…，xn），g（x1，…，xn）∈k[x1，…，xn]，則

我們看到要求解f（x1，…，xn）與g（x1，…，xn）的最大公因式，我們可以先求出兩個理想的交的既約Gr?bner基，它就是f（x1，…，xn）與g（x1，…，xn）的最小公倍式，再根據定理2我們可以直接求出f（x1，…，xn）與g（x1，…，xn）的最大公因式.

下面通過一個例子來檢驗本文的方法.

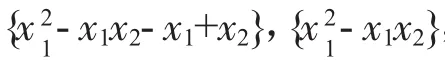
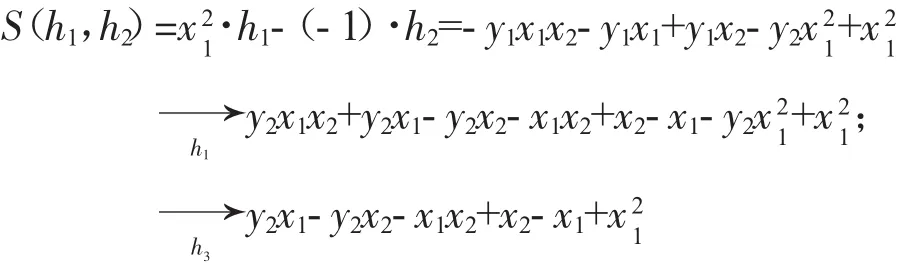
[1]何青.計算代數[M].北京：北京師范大學出版社，1997.

[2]譚宜家，陳錦松.關于多元多項式的最大公因式[J].上饒師范學院學報，2006（6）：9-11.

[3]李立.關于多元多項式的最小公倍式[J].哈爾濱商業大學學報（自然科學版），2008，24，12：123-126.

[4]B.Buchberger，G.E.Collins and R.G.K.Loos editors.Computer Algebra.Symbolic and Algebraic Computation[J].Springer Verlag，1982.

[5]樊愷.關于多元多項式可約性的討論[J].武漢教育學院學報，1998，17（6）：6-8.

The Greatest Common Factors of Polynomials in Several Indeterminates

LIU Jin-wang，HE Xiu-xiu
（School of Mathematics and Computation Science，Hunan University of Science and Technology，Xiangtan，Hunan 411201）

In this paper，the authors explores how to solve the greatest common factorsof two polynomials in several indeterminates over polynomial rings.The authors studied the association among the intersection of ideals，the greatest common factors and the least common multiple.Based on the theory and methods of basis，the authors summed up the relationship between the intersection of ideals and the least common multiple.Then，the authors give effective methods and algorithm of solving the greatest common factors.In the end of this paper，a numerical example is given to illustrate the effectiveness of our method.

polynomials in several indeterminates；multivariate polynomial rings；the greatest common factors

O15

A

1671－9743（2016）11－0010－04

2016-09-23

2016年湖南省研究生科研創新項目（CX2016B533）.

劉金旺，1964年生，男，教授，博士，博導，研究方向：線性代數.何秀秀，湖南科技大學數學與計算科學學院碩士研究生.