實現(xiàn)離散Hilbert變換所需階數(shù)的分析

陳 喆, 王 睿, 李小兵, 郭成安, 馬曉冬

(1. 大連理工大學(xué) 信息與通信工程學(xué)院， 遼寧 大連 116023) (2 . 富士通元器件科技發(fā)展有限公司， 遼寧 大連 116023)

實現(xiàn)離散Hilbert變換所需階數(shù)的分析

陳 喆1, 王 睿1, 李小兵1, 郭成安1, 馬曉冬2

(1. 大連理工大學(xué) 信息與通信工程學(xué)院， 遼寧 大連 116023) (2 . 富士通元器件科技發(fā)展有限公司， 遼寧 大連 116023)

連續(xù)信號與離散信號的Hilbert變換之間存在偏差，不利于學(xué)生理解。本文從理論上分析了信號的最高頻率、采樣頻率、想要達到的信噪比與離散Hilbert變換項數(shù)之間的關(guān)系，給出了離散Hilbert變換的特性及適用于實驗的項數(shù)確定依據(jù)。數(shù)值仿真表明了相關(guān)結(jié)論的正確性。

Hilbert變換；數(shù)字信號處理

0 引言

Hilbert變換是信號分析與處理中的有力工具，在信號處理、時頻分析等領(lǐng)域得到了廣泛應(yīng)用[1, 2]。在隨機信號分析類課程中，Hilbert變換也是主要講授內(nèi)容之一。為了強化學(xué)生對Hilbert變換的理解，特別是其在窄帶信號處理中的作用，常常輔之以實驗或數(shù)值計算結(jié)果作為演示。目前，Hilbert變換的具體實現(xiàn)多基于離散時間數(shù)據(jù)，用Matlab編程來實現(xiàn)。

連續(xù)時間信號x(t)的Hilbert變換定義為

(1)

其中，‘*’表示卷積。理論上，Hilbert變換可等效為x(t)通過一單位沖激響應(yīng)為h(t)=1/πt的濾波器的輸出，這里h(t)的Fourier變換為

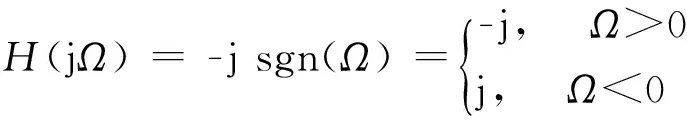
(2)

上述連續(xù)時間信號的Hilbert變換物理概念清晰，在國內(nèi)外相關(guān)教材中都有較為詳細的介紹[1, 2]。與上述H(jΩ)類似，離散Hilbert變換等效濾波器h(n)的離散時間Fourier變換定義為[3, 4]

(3)

h(n)的單位脈沖響應(yīng)為

(4)

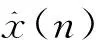
(5)

與h(t)類似，h(n)也是非因果濾波器，兩者皆在物理上不可實現(xiàn)，因此在實際應(yīng)用時……