雙陷波補償算法在火箭推力矢量控制中的擴展應用

孫 毅，幺志剛，盧紅影，李 昌，周海強

?

雙陷波補償算法在火箭推力矢量控制中的擴展應用

孫 毅，幺志剛，盧紅影，李 昌，周海強

（北京精密機電控制設備研究所，北京，100076）

針對單陷波補償算法濾波帶寬較窄的問題，提出將雙陷波補償算法應用于單諧振點發動機伺服機構控制并建立了數學模型。仿真結果表明，雙陷波補償算法能夠在較寬范圍內相對有效地抑制諧振峰，且其低頻段相角與單陷波補償算法相比滯后并不明顯。為驗證分析的正確性，在試驗臺上對伺服機構進行陷波補償算法試驗，為雙陷波補償算法在火箭推力矢量控制中的擴展應用奠定基礎。

伺服機構；雙陷波補償；諧振峰

0 引 言

物質的固有頻率與其振動頻率接近時，容易發生共振現象。火箭發動機也是如此，但其諧振現象更加復雜，因為火箭發動機不僅剛度分布不均且轉動慣量較大，只能由伺服機構承擔抑制諧振的任務（通過伺服機構掃頻測試，得到角位移與線位移輸出頻率特性，再進行比較運算，即可得到發動機的諧振特性）[1~3]。對伺服機構采用陷波補償控制算法或采用具有動壓反饋的伺服閥是常用的抑制負載諧振的有效手段[4~6]。與動壓反饋相比，陷波補償算法能夠省去壓差傳感裝置，不僅具有成本控制的優勢，而且參數調節靈活，采用陷波補償算法抑制負載諧振是未來發展的方向。

在運載火箭的研制過程中，發現有些火箭發動機的頻率值在某一范圍內僅有一個諧振峰，即僅具有一個固有頻率，而有些液體火箭發動機的頻率值在某一范圍內會出現2個諧振峰，即具有2個固有頻率，對于后者而言，如果采用單陷波的凹口補償算法已不能對具有2個諧振峰的諧振進行很好地抑制，于是出現了雙凹口的陷波補償算法[1]；對于具有雙諧振點的發動機而言，仿真和試驗證明雙陷波補償算法更適于伺服機構的諧振抑制，可以有效地控制不同頻段的幅值和相角。

然而將雙陷波補償算法擴展應用于僅具有單個諧振峰的火箭發動機的伺服機構負載諧振抑制中會產生何種效果，尤其是在單陷波補償算法因濾波帶寬較窄而無法在大范圍頻段內有效抑制諧振峰的情況下，對于這一問題國內外較少研究。本文以此為出發點，對僅具有單個諧振點的發動機伺服機構的控制分別進行單點陷波和雙點陷波補償算法的仿真和試驗，并對二者造成的影響進行分析和比較，為雙陷波補償算法在火箭推力矢量控制中的擴展應用奠定基礎。

1 控制模型

某Ⅰ級大功率伺服機構與發動機負載模擬臺的聯接方式如圖1所示。由圖1可知，箭上計算機將控制指令發送至伺服機構，伺服機構的活塞桿根據控制指令要求產生位移（伸、縮），驅動發動機噴管（或模擬負載）擺動，改變推力矢量方向，實現姿態穩定與控制。

圖1 伺服機構與發動機的聯接方式

圖2為采用單陷波補償算法的火箭發動機伺服機構的控制回路模型。由圖2可知，箭上計算機輸入位置指令至控制器，位置指令在控制器中進行算法補償并轉換成電流信號，電流信號作用于伺服閥并控制伺服閥的輸出流量，從而驅動伺服機構的活塞運動。反饋電位計將活塞的位移轉換為電壓信號，反饋到數字伺服控制器，由伺服控制器完成輸入指令與位移反饋信號的綜合，實現數字閉環，控制伺服作動器執行相應動作[7,8]。

圖2中采用的是最基本的單陷波補償環節，傳遞函數為

陷波補償的原理是將式（1）中零、極點替換，即把低阻尼比的一對極點和替換為較高阻尼比的另外一對極點和，從而改善系統的穩定性[1]。

采用雙陷波補償算法時，對應的傳遞函數為

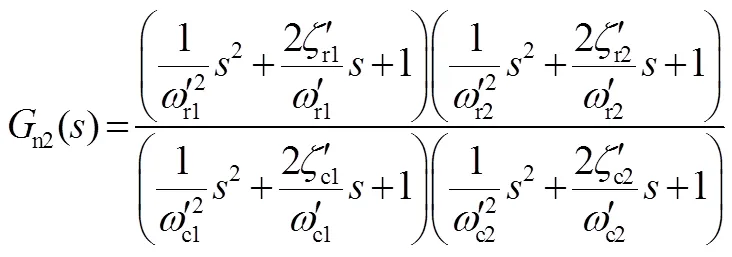
雙陷波補償算法的伺服機構控制回路模型如圖3所示。比較圖3與圖2可以看出，除了補償算法的區別外，圖3和圖2只有作動器的負載效應和發動機的負載特性不同。若將雙陷波補償算法應用于僅具有單個諧振峰的火箭發動機的伺服機構控制回路中，則此時的模型如圖4所示。

圖2 單陷波補償算法在單諧振點發動機伺服機構控制中的模型

圖3 雙陷波補償算法在雙諧振點發動機伺服機構控制中的模型

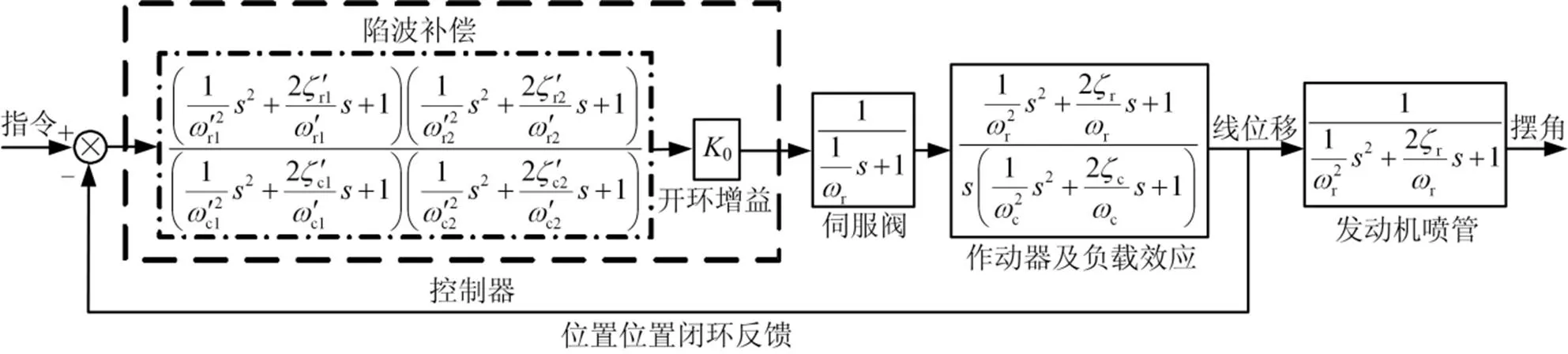
圖4 雙陷波補償算法在單諧振點發動機伺服機構控制中的模型

2 仿真分析

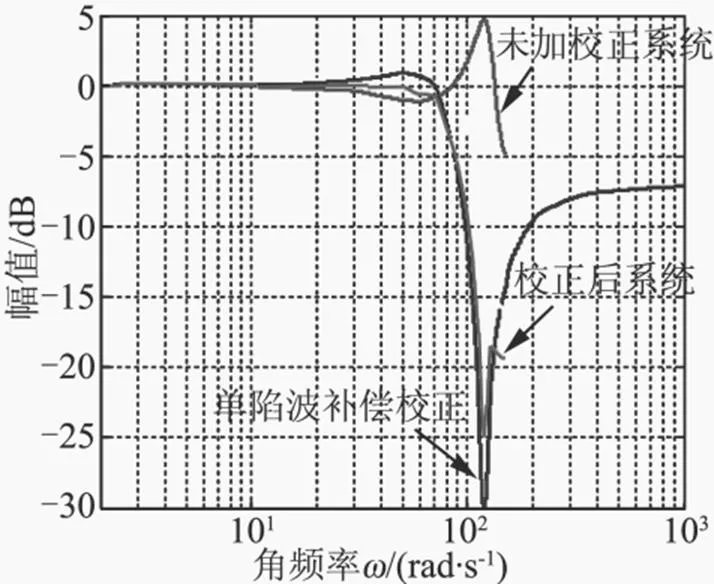
根據上述伺服機構控制模型，對僅具有單個諧振峰的火箭發動機的伺服機構頻率特性進行仿真，并將加入單陷波補償前、后伺服機構的頻率特性曲線進行比較，如圖5所示。

a）幅頻

b）相頻

圖5 加入單陷波補償前、后伺服機構的頻率特性

由圖5a可看出，未加校正系統的幅值在低頻段時基本保持不變，之后略有下降，再出現一個明顯凸起的諧振峰，單陷波補償校正的作用是在出現諧振峰的頻段區通過產生一個幅值凹陷點抵消諧振峰，可以看出校正后的系統在高頻段的幅值得到明顯地抑制。由圖5b可看出，在加入單陷波補償算法后系統相角較未加補償前出現不同程度的滯后，說明單陷波補償算法對相位特性有負面影響。由此可見，將單陷波補償算法應用于僅具有單個諧振峰的火箭發動機的伺服機構負載諧振中的方法有效，但不能同時改善相角和幅值。

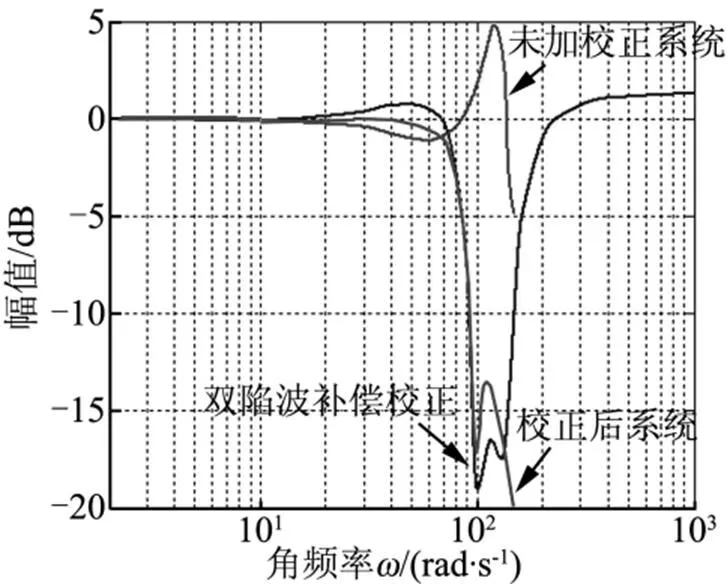
圖6為加入雙陷波算法補償校正前、后伺服機構帶載的頻率特性曲線。由圖6可以看出，雙陷波算法補償校正的原理與單陷波算法補償校正相似，同樣是在諧振峰對應的頻段范圍內以幅值凹陷的形式抵消諧振峰，但與單陷波補償不同的是凹陷區有2個凹點，并且相位曲線中有2個明顯的凸起滯后點。

a）幅頻

b）相頻

圖6 加入雙陷波補償前、后伺服機構的頻率特性

為了對單陷波補償和雙陷波補償的效果更直觀地比較，將單陷波補償與雙陷波補償算法放在一起進行區分，如圖7所示。

從圖7a可以看出，雙陷波補償算法有2個凹點，且凹陷區最底端由2個凹點形成的寬度要明顯大于單諧振補償算法的凹陷區由一個凹點形成的寬度，這說明相同條件下雙陷波補償算法能夠在更寬的頻段范圍內對系統的幅值進行抵消和抑制。但由于2個凹點的深度均較單陷波補償算法的單凹點淺，因此就諧振頻率點的補償效果而言，雙陷波不如單陷波補償算法。從圖7b可以看出，當低頻段時單、雙陷波補償算法的區別不大，但當進入中頻段之后雙陷波補償比單陷波補償的相角滯后會有所增加，此時單陷波補償算法的相角指標較雙陷波補償變優，高頻段時雙陷波補償和單陷波補償的相角均大幅上揚，此時不具有應用意義。

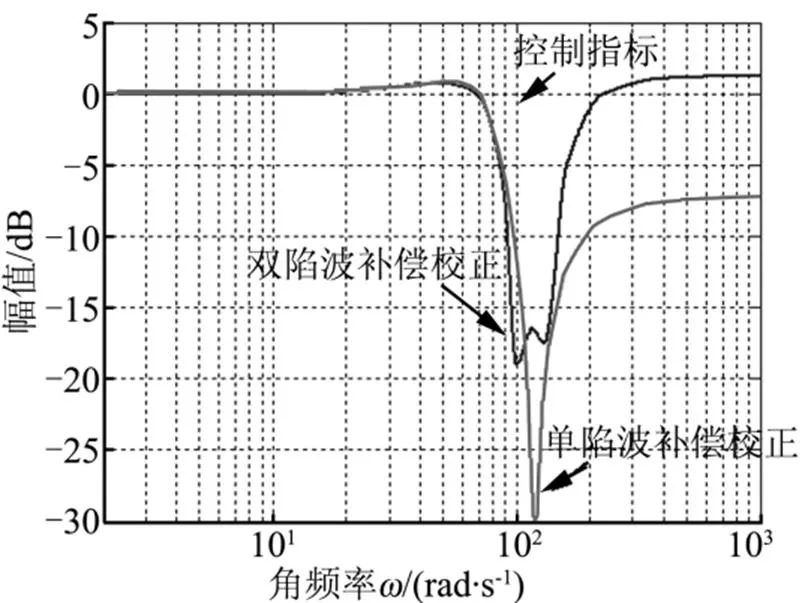
a）幅頻

b）相頻

圖7 單、雙陷波補償對伺服機構的頻率特性

3 試驗驗證

為驗證理論分析和仿真的正確性，利用發動機噴管負載模擬臺對單諧振點負載條件下的伺服機構控制算法進行試驗，分別采用單陷波補償算法和雙陷波補償算法并對二者進行比較，得到負載模擬臺實測角位移頻率特性試驗曲線，如圖8所示。

a）幅頻

b）相頻

圖8 角位移頻率特性

由圖8可以看出，經過陷波補償算法后的幅值在高頻段的衰減較仿真曲線更明顯，說明實際陷波補償中對幅值的抑制作用比仿真中的還要明顯。這是因為對伺服機構控制模型中的某些模塊進行了簡化，并且個別參數設置的準確性還有待進一步提高，但總的來說試驗曲線和仿真曲線的趨勢是一致的。

雙陷波補償較單陷波補償能夠在更寬的范圍內對系統諧振點附近的幅值產生抑制作用，但就諧振點而言，單陷波補償的抑制效果比雙單陷波補償明顯；在相位的滯后性上，單陷波補償優于雙陷波補償，但二者在低頻段的區別并不明顯。

4 結 論

針對單諧振點發動機難以將諧振點準確定位的問題，提出將雙陷波補償算法應用于單諧振點發動機伺服機構控制的研究方法，擴展了雙陷波補償算法在火箭推力矢量控制中的應用范圍，建立了雙陷波補償算法在單諧振點發動機伺服機構控制中的數學模型，并就雙陷波和單陷波的補償效果進行了仿真和試驗。結果表明：雙陷波補償較單陷波補償能夠在更寬的范圍內對系統諧振點附近的幅值產生抑制作用，但就諧振點而言，雙陷波補償的抑制效果不如單陷波補償明顯，在相位的滯后性方面，單陷波補償優于雙陷波補償，但二者在低頻段的區別并不明顯。

[1] 尹傳威, 趙守軍, 陳克勤. 雙諧振點發動機推力矢量控制伺服機構算法優化研究[J]. 導彈與航天運載技術, 2013(1): 21-26.

[2] 黃效國, 程建中, 崔勇. 使用軟件動壓反饋提高大慣性負載液壓伺服系統穩定性[J]. 液壓與氣動, 1994(4): 10-13.

[3] 趙迎鑫. 大運載助推級伺服機構真實發動機負載動態模型的獲取和辨識[C]. 北京: 第五屆全國流體傳動與控制學術會議, 2008.

[4] 蔡璞, 許化龍, 夏克寒. 導彈液壓伺服系統中陷波器的原理與設計[J]. 導彈與制導學報, 2006, 26(2): 148-149.

[5] 黃翔東, 王兆華, 呂衛. 陷波頻率點可精確控制的高效FRM陷波器設計[J]. 系統工程與電子技術, 2009, 31(10): 2320-2322.

[6] 黃效國, 程建中, 崔勇. 使用軟件動壓反饋提高大慣性負載液壓伺服系統穩定性[J]. 液壓與氣動, 1994(4): 10-13.

[7] 葉宏, 曾廣商. 三余度數字伺服控制系統建模與動靜態特性研究[J]. 固體火箭技術, 2003, 26(1): 71-75.

[8] 曾廣商, 沈為國, 石立, 張曉莎. 高可靠三冗余伺服機構系統[J]. 航天控制, 2005(1): 35-40.

Research on Extended Application of Double-notch Compensation Algorithm for Rocket Thrust Vector Control

Sun Yi, Yao Zhi-gang, Lu Hong-ying, Li Chang, Zhou Hai-qiang

(Beijing Institute of Precision Mechatronics and Control Equipment, Beijing, 100076)

Aiming at the problem of single-notch with narrow bandwidth, a double-notch compensation algorithm was applied to the servo-mechanism of single resonance engine. The mathematical model of the double-notch filter was established. Simulation results showed that the resonance peak was effectively inhibited, and the phase delay was improved compared to the single-notch filter. Experiments on notch compensation algorithm were carried out at test rig to verify the simulation model, and laid the foundation for the application of double-notch compensation algorithm on rocket thrust vector control.

Servo-mechanism; Double-notch compensation; Resonance peak

1004-7182(2016)03-0077-04

10.7654/j.issn.1004-7182.20160318

V433

A

2016-01-05；

2016-03-15

孫 毅（1979-），男，博士，工程師，主要研究方向為液壓元件與系統的優化設計