解析高中數學中的基本函數
彭勇
【摘 ? ?要】基本初等函數,是高中學習的主要內容之一,同時,也是高中學習的重點之一。基本初等函數包括:指數函數、對數函數、冪函數,三大函數之間的聯系與區別便是學生要掌握的要點。數學老師在函數的教學計劃中都分配了較多的課時,誠然,函數的學習是數學的重點,那么解析基本初等函數就能在一定程度上幫助學生更加深入的理解數學理論。
【關鍵詞】高中數學 ?基本初等函數 ?解析 ?考點 ?理論
中圖分類號:G4 ? ?文獻標識碼:A DOI:10.3969/j.issn.1672-0407.2016.03.084
函數是高中階段數學學習的重點內容之一,其運算的復雜性讓很多學生難以掌握,對學生的全面發展造成了一定的影響。在此,我將結合自身的教學經驗對高中的基本函數進行相關的解析,希望對大家有所幫助。
一、初等函數的學習要求
1.能進一步體會函數是描述變量之間的依賴關系的重要數學模型,在此的基礎上學習用集合與對應的語言來刻畫函數,體會對應的關系,刻畫函數概念中的作用。此外,了解構成函數的要素,會求一些簡單函數的定義域和值域。同時,了解與學習函數時,也要了解映射的概念,這樣觸類旁通式的學習,才能讓數學的教學變得更加簡捷。
2.學生能在實際情景中,根據不同的需要選擇恰當的方法。例如,圖像法、列表法、解析法等表示函數,會求解函數的基本表達式,以及表達式中參數所表示的意義。
3.了解簡單的分段函數的定義、形式、結構,并且能根據已經了解到的知識,進行具體的實際操作。
4.能夠通過已經學習過的函數,特別是像二次函數,理解函數的單調性、最大值、最小值以及它們的幾何意義,還能結合具體函數,了解奇偶性的含義。
5.學會運用函數圖像理解和研究函數的性質。函數既是解決問題的方法,同時,也是解決問題的手段,面對不同的問題,會有不一樣的方法來解決。一般能用函數解決的問題,都會是用函數來解決,不僅因為函數的直觀可見,而且函數能形象地將問題反映在一張圖表上。讀者想要的答案,就在圖表隱藏的位置,只要稍微地動動腦筋,答案便就出來了。誠然,函數的學習是重要的。教師培養學生看圖、讀圖、解圖“三步走”的能力,同時,也是培養學生轉換思維的能力。
二、指數函數
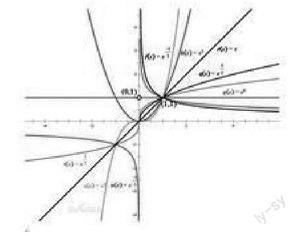
指數函數是數學中重要的函數之一。它的一般的形式為:y=a^x(a>0且a≠1)(x∈R)。此外,還會應用到e上的這個函數寫為exp(x),還可以等價寫為e,這里的e是數學常數,就是自然對數的底數,近似等于2.718281828,稱為歐拉數。下面是指數函數的圖像:
對于初等函數中指數函數的學習,特別要掌握指數函數的圖形,以及它的基本表達式的寫法,因為,指數函數的圖像是屬于比較復雜的一類。由上圖可知:它的圖像關于y軸對稱,不同a的大小,圖形曲線的表達形式也不一樣。需要分類討論即:
1.由指數函數y=a^x與直線x=1相交于點(1,a)。在y軸的右側,圖像從下到上相應的底數由小變大。
2.由指數函數y=a^x與直線x=-1相交于(-1,1\a)。在y軸左側,圖像從下到上相應的底數由大變小。
3.指數函數的a一定是大于零,當a>1時,指數函數對于x的負數值非常平坦,對于x的正數值迅速攀升,在x等于0的時候y等于1。
當然,指數函數只是一種解決問題的方法或者稱為手段,歸為本質的便是:回歸課本,解決課本中的問題,卷子的試題,解決在實際生活中遇到的數學問題。最主要的還是,學生自身對知識的不斷積累與拓展,最終使得自己在同一學習環境中出類拔萃,同時在高考中出類拔萃,斬獲高分。
對此,了解指數函數的實際應用能幫助學生更好地學習函數的具體應用,在教師的教學中,學生也能配合教師的教學計劃,將課堂更好地利用。指數函數的實際應用是非常廣泛的。例如,細胞的分裂、考古中所用的c的衰減、藥物在人體內殘留量的變化等。具體的問題具體分析,對于不同的實際問題,學生要學會歸納與總結,將同一類的問題歸一為一個具體的模型,以便以后再遇到此問題時,能很快速地解決問題。
三、對數函數
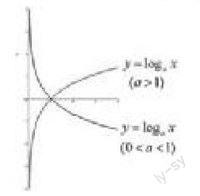
一般如果a(a大于0,且a不等于1)的b次冪等于N(N>0),那么數b就叫做以a為底N的對數。記作logaN=b。對數函數的圖像為:
對數函數的實際應用沒有指數函數那么多,相反的,對數函數的題型更多的是,掌握對數函數的性質的應用,會利用對數函數的性質,解決變形的題目,達到邏輯思維的高度訓練;不斷鍛煉學生自己縝密的解題思路,從而做到細節完美化。
對于對數函數的性質,是高中函數教學計劃中必須掌握的內容。對數函數最多的題型是:利用其性質轉換題型,然后解題。誠然,性質的學習、理解、掌握是第一步,根據對數函數的運算性質,可以很快速地得出兩個函數值之間的大小關系。如果底數一樣,真數越大,函數值越大。(a>1時)如果底數一樣,真數越大,函數值越小。(0 當a>0且a≠1時,M>0,N>0,那么: (1)log(a)(MN)=log(a)(M)+log(a)(N); (2)log(a)(M/N)=log(a)(M)-log(a)(N); (3)log(a)(M^n)=nlog(a)(M) (n∈R). 四、冪函數 冪函數的基本形式為:y=x^a(a為常數),即以底數為自變量,冪為因變量,指數為常量的函數稱為冪函數。冪函數與指數函數,不外乎就是將底數與指數進行轉換,因此,指數函數與冪函數的聯系最為密切,通過指數函數的圖像,可以類比推出冪函數的圖像。對于每一個函數的學習,圖像是能直觀與形象地展示函數性質的最好的表達形式之一,誠然,圖像的學習也是在教學大綱中,被教師經常提及的。以下便是冪函數的圖像: 對于冪函數,教師較為注重的是:冪函數的常數a,因為不同的a對應的函數的圖形存在差異,因此,冪函數的圖像是三個初等函數中,最為復雜的一個。同時,冪函數的應用最多的也是不同a值所對應的圖形,然后利用圖形解決變換問題。 五、三者之間的解析 對于高中數學的學習,不僅是難度的加深,深度的變廣,范圍的擴大,更是一種思維的訓練。像數學中的集合、空間幾何體、點、直線、平面之間的位置關系、圓與方程等等知識的范圍越來越多。學習的難度越來越深,對于函數的學習,也是如此。正確把握函數之間的關系與邏輯思維,掌握解題的思路與技巧,函數之間的聯系與區別,將函數的模型運用到實際的生活問題當中來,無論是指數函數、對數函數還是冪函數,它們的運用價值都是極其大。 將指數函數、對數函數、冪函數的圖像,進行分析、對比然后總結出各個圖像之間存在的差異,以及它們之間的聯系,會從它們基本的形式結構、函數的單調性、奇偶性、周期性、連續性、凹凸性等不同的指標,正確分析每一個函數的特點,然后能準確掌握,并運用。 近幾年,隨著課改腳步的推進,數學的學習越發變得緊張。高中面臨的問題,畢竟是高考,所以教師需要在了解改革體制的同時,加強教育教學模式,不斷進取、不斷創新、不斷開拓,為學生的學習提供更加優秀的教學計劃。

