軸重30 t重載列車作用下新黃土區隧道適應性及強化措施研究

劉聰，彭立敏，雷明鋒，施成華

(中南大學 土木工程學院，湖南 長沙 410075)

?

軸重30 t重載列車作用下新黃土區隧道適應性及強化措施研究

劉聰，彭立敏，雷明鋒，施成華

(中南大學 土木工程學院，湖南 長沙 410075)

摘要:以在建的蒙華鐵路典型隧道結構型式為基礎，針對新黃土區重載鐵路隧道結構動力響應、疲勞壽命以及合理強化措施等問題，采用數值模擬的方法進行研究。結果表明：隨著軸重和運量的增加，既有鐵路隧道無法滿足30 t軸重列車長期安全運營的要求，應采取強化措施。而單一的系統錨桿注漿加固強化能力有限，須采用系統錨桿與隧底地基加固(加固深度4 m及其以上)的聯合強化措施方能滿足其疲勞壽命要求。通過研究，指出30 t軸重列車荷載作用下隧底結構疲勞易損位置，即二次襯砌仰拱中心、初期支護仰拱與邊墻連接處，并得到滿足100 a設計使用年限，新黃土區隧道二次襯砌、初期支護混凝土結構在軸重30 t列車荷載作用下的疲勞上限強度，分別為1.30和1.62 MPa，可為設計參考。

關鍵詞：30 t軸重；重載鐵路隧道；適應性；疲勞壽命；強化措施

重載鐵路以其高運量、低成本的優點，越來越受到世界各國鐵路建設者的青睞。相比于普通鐵路，重載列車的軸重更大，線下結構承受的動力沖擊也更大，這無疑增加了基底病害的發生概率。在重載鐵路隧道中，隧底結構在重載列車作用下更容易產生疲勞累積損傷，以致影響行車安全。據調查，我國重載鐵路—大秦線自開通以來，隨著軸重及運量的增加，多座隧道出現了不同程度的基底破損和翻漿冒泥等病害，且有逐年加重的趨勢[1]。可見，既有鐵路隧道對列車軸重增加的適應能力尚有待提升。也正因為如此，近年來，國內外眾多學者對該問題開展了廣泛研究。在病害調查分析方面，牛亞彬[1]對朔黃重載鐵路77座隧道病害進行統計，并采用數值計算、現場試驗等手段分析相關病害的形成機理和發展規律，給出了相應的處治對策。馮冀蒙等[2]對不同時期、不同地質條件下隧道的病害產生規律進行統計分析。在數值模擬研究方面，王秀英等[3]采用有限元方法分析得到軸重30 t列車荷載作用下隧道二次襯砌的動力響應特征。在現場動力實測方面，付兵先等[4]對朔黃重載鐵路三家村隧道進行了現場測試，獲得不同圍巖區段填充層頂面處的動壓應力幅值。在隧道結構長期服役性能研究方面，黃娟[5]從疲勞累積損傷的角度出發，研究引起鐵路隧道結構產生疲勞損傷的主要原因，指出圍巖條件對二次襯砌仰拱的動力響應和動力損傷影響較顯著。Lei等[6]針對列車長期反復荷載作用下巖溶地基的累積沉降變形問題進行了分析，指出經處理后的巖溶區隧底結構累積變形值不會對列車長期運營安全造成破壞性影響。晏偉光[7]采用數值模擬方法分析不同軸重、不同設計參數對隧底疲勞壽命的影響。徐新利等[8-9]分別以朔黃重載鐵路隧道工程為背景，研究軸重30 t列車荷載作用下基底吊空、欠密實病害對隧底結構受力的影響。諸如此類的研究還有很多[10]，相關研究成果也為我國重載鐵路建設提供了有益參考。但縱觀這些研究成果，尚沒有見到新黃土區重載鐵路隧道的相關成果報道，而我國在建及規劃中的重載鐵路就存在穿越大片黃土區域的情況，可以預見，未來幾年中將有大量的黃土區重載鐵路隧道需要修建。與常規軟弱圍巖相比，新黃土動力性能差，在長期反復重載作用下，更容易出現各種結構病害。因此，針對黃土區重載鐵路隧道的動力特性和疲勞壽命問題開展相關研究具有重要的前瞻意義，可為我國即將或正在興建的黃土區重載鐵路隧道提供參考。

1動力計算模型

1.1典型黃土區重載鐵路隧道結構型式

在建的蒙華重載鐵路沿線經過大量黃土地區，相應的隧道工程具有代表性和典型性，故可作為研究對象。典型的黃土區隧道結構型式如圖1。

1.2數值模型的建立

采用大型有限元軟件建立隧道-圍巖耦合三維計算模型。模型中模擬2節軸重30 t重載列車以72 km/h的速度通過長30 m的隧道，且考慮雙線同時加載。模型范圍水平方向以隧道左右側外邊緣向外延伸50 m，豎直方向自隧道底部向下取75 m，自隧道拱頂向上取至地表，地表埋深按淺埋考慮，埋深取15 m，如圖2。

考慮不同地質年代、孔隙率和含水率等的黃土力學性能差異很大，本文研究中圍巖僅取新黃土，且為服從Mohr-Coulomb屈服準則的彈塑性材料；初期支護、二次襯砌、填充層、底座板、彈性墊層、軌道板和鋼軌等隧道結構均采用實體單元，僅按線彈性材料考慮。相關計算參數取值見表1。

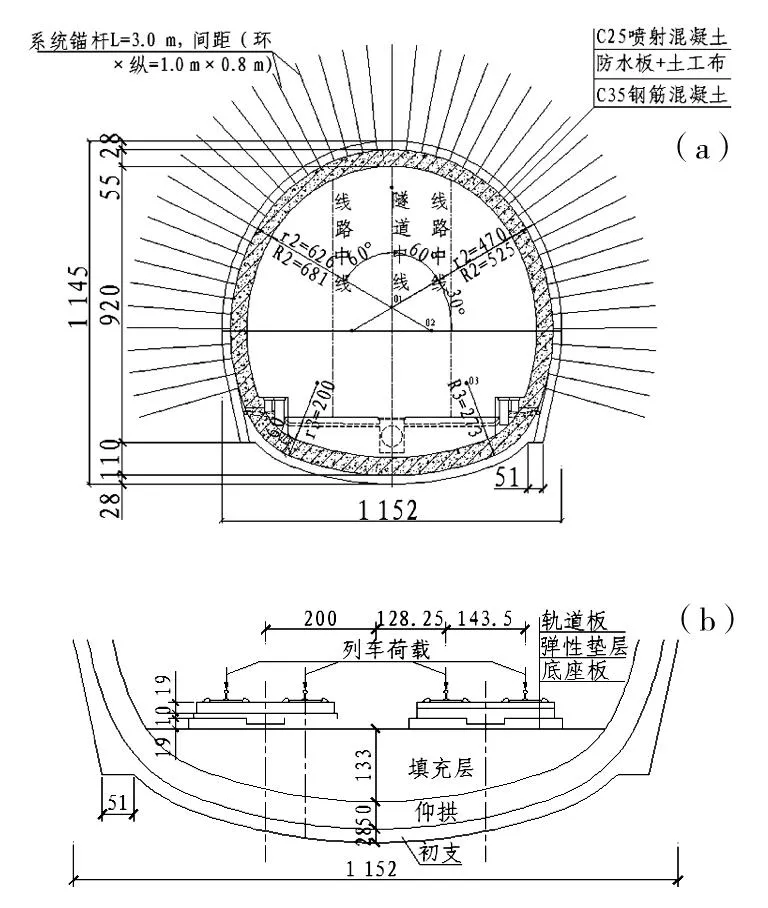
(a)橫斷面；(b)底部結構圖1　蒙華重載鐵路隧道結構設計圖Fig.1 Tunnel supporting structure of Menghua heavy haul railway

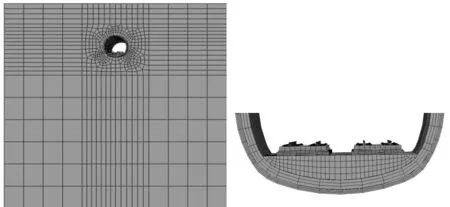
(a)整體模型 ；(b)底部結構圖2　計算模型Fig.2 Calculation model

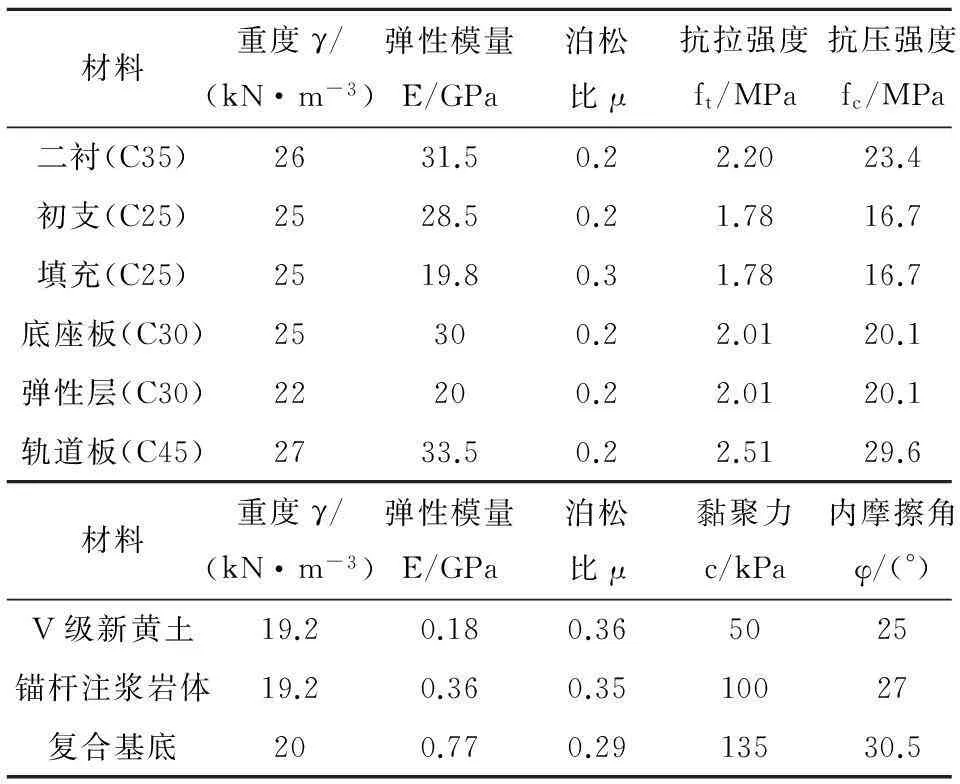
材料重度γ/(kN·m-3)彈性模量E/GPa泊松比μ抗拉強度ft/MPa抗壓強度fc/MPa二襯(C35)2631.50.22.2023.4初支(C25)2528.50.21.7816.7填充(C25)2519.80.31.7816.7底座板(C30)25300.22.0120.1彈性層(C30)22200.22.0120.1軌道板(C45)2733.50.22.5129.6材料重度γ/(kN·m-3)彈性模量E/GPa泊松比μ黏聚力c/kPa內摩擦角φ/(°)V級新黃土19.20.180.365025錨桿注漿巖體19.20.360.3510027復合基底200.770.2913530.5

1.3重載列車荷載模擬

列車荷載作用于鋼軌表面，考慮車速、軌道幾何不平順及車輪扁疤等因素導致的隨機振動帶來的附加作用力后，可近似用以下激勵函數來模擬：

F(t)=P0+P1sin(ω1t)+P2sin(ω2t)+

P3sin(ω3t)

(1)

式中:P0為車輛靜載；P1，P2和P3均為振動荷載；ωi為不平順控制條件下的振動圓頻率，對應的典型值可參見文獻[11]。

列車為軸重30 t煤炭敞車，如圖3。于是，可得到30 t軸重列車通過隧道時軌下反力時程曲線即列車荷載譜曲線，如圖4。

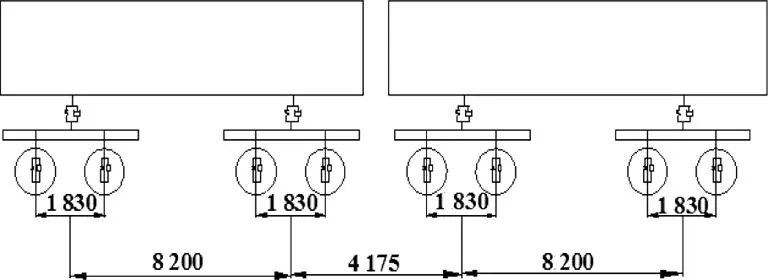
圖3　30 t軸重車輛軸距圖Fig.3 Wheelbase of 30 t axle train

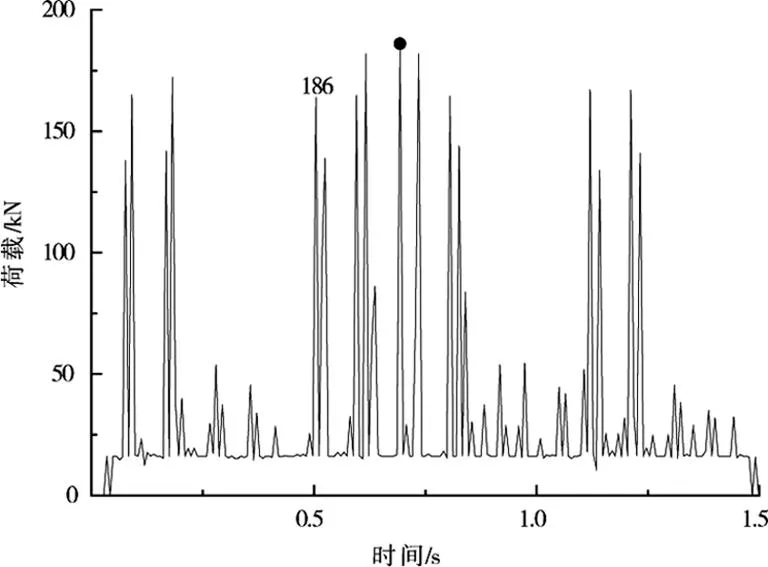
圖4　30 t軸重列車荷載譜Fig.4 Load spectrum of 30t axle train

1.4混凝土疲勞壽命曲線

疲勞壽命曲線(即S-N曲線)是以試驗數據為基礎，統計某種等幅應力循環作用下直至結構產生疲勞破壞所能經受的最大循環次數，S代表材料或結構的應力水平，可以用最大應力水平Smax和最小應力水平Smin等來表示，如Smax=σmax/fc；N表示疲勞壽命，即疲勞失效時的循環加載次數，一般可用lgN來表示，典型的混凝土疲勞壽命曲線如圖5所示。

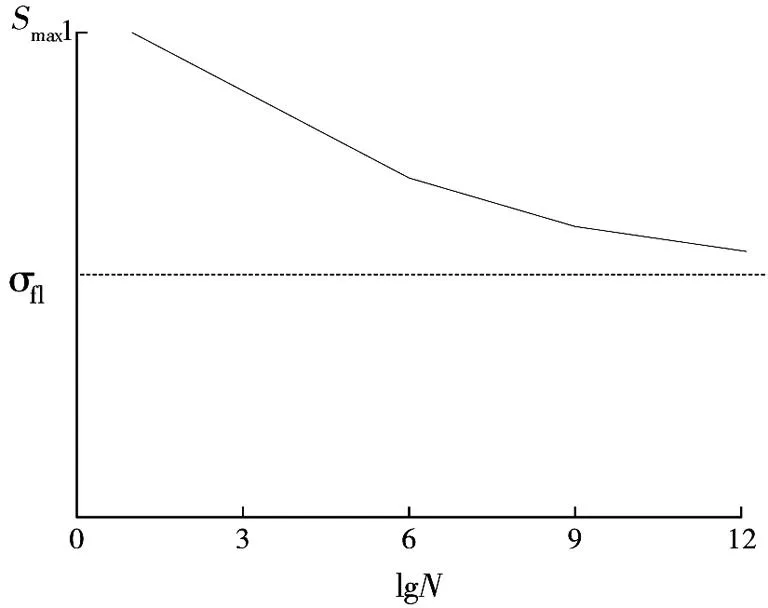
圖5　疲勞壽命曲線(S-N曲線)Fig.5 Fatigue life curve (S-N curve)

我國混凝土結構設計規范對混凝土結構疲勞壽命僅作了定性要求[12]，而歐美等發達國家通過大量的混凝土疲勞試驗，給出了相對成熟且詳盡的疲勞壽命曲線[13]。對于處于純拉狀態下的素混凝土：當0≤St,min≤0.8時，在等應力幅度作用下的混凝土疲勞壽命(Ncf)通過式(2)確定；當St,min>0.8時，可采用St,min=0.8時的S-N曲線。

(2)

其中：

1) 若lgN1≤6，則lgNtf=lgN1；

2) 若lgN1>6，且ΔSc≥0.3-0.375St,min，則lgNtf=lgN2；

3) 若lgN1>6，且ΔSt≤0.3-0.375St,min，則lgNtf=lgN3。

式中：St,max為混凝土最大拉應力水平；St,min為混凝土最小拉應力水平；ΔSt為混凝土應力幅度。上述公式同樣適用于計算拉-壓或純壓狀態下素混凝土的疲勞壽命[13]。

1.5疲勞累積損傷

計算得到結構的動力響應后，需要對其應力循環進行統計，并結合Miner累積損傷理論來對隧底結構的疲勞損傷情況。Miner線性疲勞累積損傷理論認為各應力循環作用所產生的損傷互不相關，每種應力循環所產生的疲勞損傷只與其循環次數有關，與加載順序無關，各種不同應力循環產生的損傷可以線性疊加，當累積值超過某一定值時，結構將發生破壞，不同應力循環產生的累積損傷值可按下式進行計算：

(3)

式中：D為疲勞累積損傷值；Ni為某一應力水平下產生疲勞破壞的循環次數；ni為結構經受該應力水平的循環次數。

以蒙華鐵路遠期設計為例，該線路每列列車運量為2萬t，年運量2億t，設計使用年限為100 a，總的運量為200億t，則隧道在設計使用年限內將1×106列列車通過，可得到隧道100 a內經受的總應力循環次數。當隧道在100 a內經受的總的應力循環所產生的疲勞累積損傷值不大于1時，則能適應重載列車在設計使用期內的安全運營。

2隧底結構動力響應分析

2.1僅考慮列車動載的隧底結構動力響應

盡管市場不斷擴大、業務不斷增長，IoT仍處于技術發展的初期，依舊面臨一系列的安全隱患，龐大的數量和自身的脆弱性使得IoT設備極易成為黑客的首選目標。電影《速度與激情8》中數以萬計的智能車輛被“天眼”系統惡意操控，進而組成“僵尸車聯網”圍剿國防部長；再如，2016年下半年，Mirai病毒控制超過30多萬臺的IoT設備對Dyn公司、OVH公司發動大規模分布式拒絕服務（DDoS）攻擊，致使164個國家或地區受到影響。因此，IoT產業化的日益加速與技術的安全可信之間的矛盾成為該領域急需解決的重要問題，也是推動新型IoT技術發展的重要因素之一。

圖6～7為僅考慮列車動載作用下隧底結構的動力響應時程曲線。從中分析可見，轉向架通過時隧底引起的結構動應力最大，單個輪對通過時次之。列車轉向架兩相鄰輪對通過時，會產生4個應力峰值，單個輪對通過時產生2個應力峰值。

進一步提取軌下斷面填充頂部點A1，二次襯砌仰拱頂部點A2，初期支護仰拱頂部點A3以及隧底圍巖處點A4的動力響應數據，具體點位選取如圖8，得到隧底結構動應力沿軌下深度變化規律，如圖9。

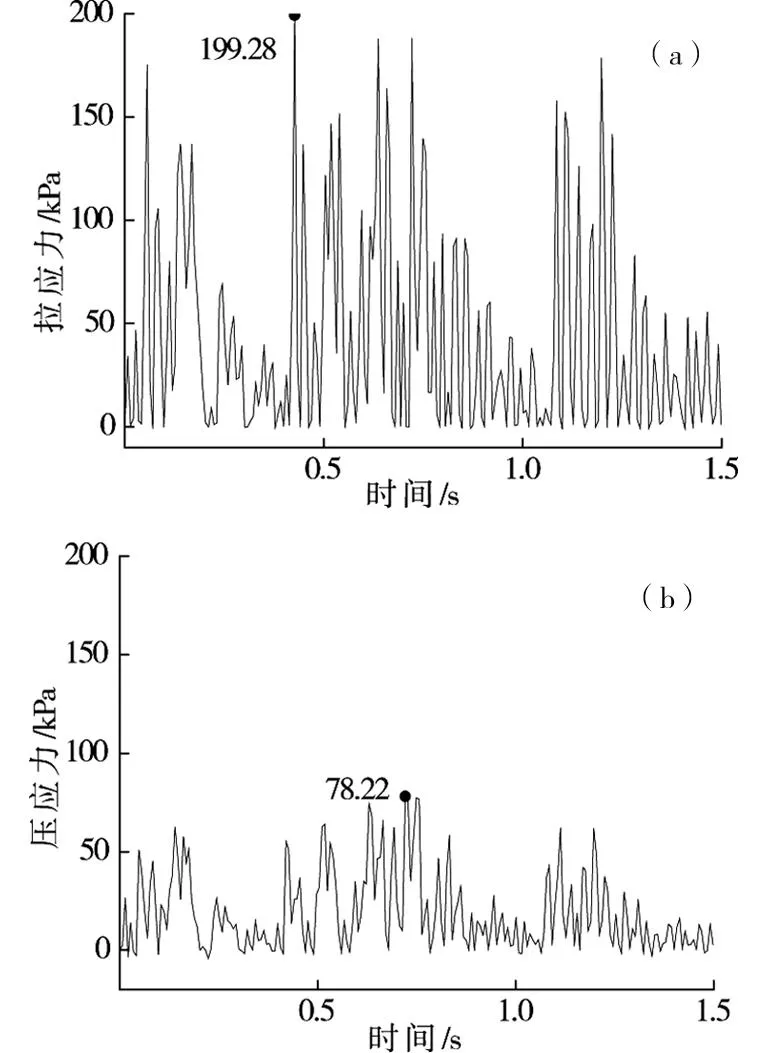
(a)拉應力；(b)壓應力圖6　隧道軌下二襯頂面應力時程曲線Fig.6 Dynamic stress time-history curves of secondary lining under the rail

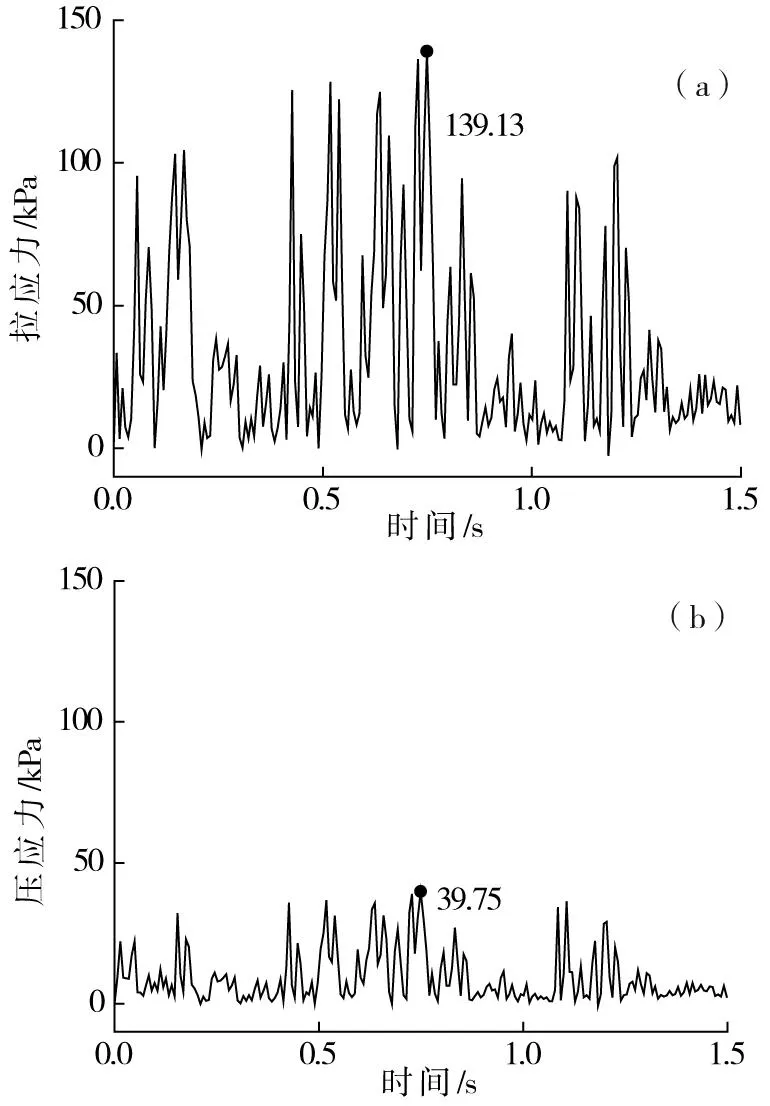
(a)拉應力；(b)壓應力圖7　隧道軌下初支頂面應力時程曲線Fig.7 Dynamic stress time-history curves of initial support

從中分析可知：1)動拉應力隨深度先增加后減小，在二次襯砌仰拱中達到峰值199.28 kPa，初期支護中拉應力次之，初期支護與土的交界面處衰減為二次襯砌仰拱隧中最大動拉應力的3.35%。2)壓應力隨深度呈線性減小，填充層頂面最大壓應力為133.5 kPa，而初期支護與土體交界面處迅速衰減為填充頂最大動壓應力的8.91%。

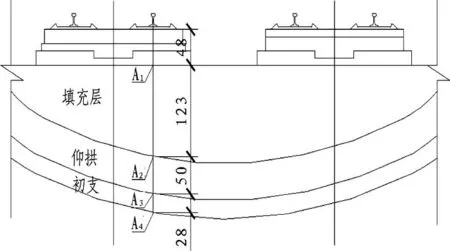
圖8　軌下斷面點位Fig.8 Points under the rail

圖9　隧底動應力沿軌下深度傳遞規律Fig.9 Dynamic stress transmission mechanism of bottom structures under the rail

2.2考慮動靜荷載耦合作用的隧底結構動力響應

隧道開挖后，圍巖壓力靜載作用將使隧道襯砌結構產生應力及變形，與列車荷載作用下的動力響應相互耦合，隧道結構在兩者耦合作用下的應力云圖如圖10～11。

(a) 拉應力;(b) 壓應力圖10　動靜荷載耦合作用下新黃土隧道二襯應力云圖Fig.10 Coupled stress contour of secondary lining after loess tunnel excavation

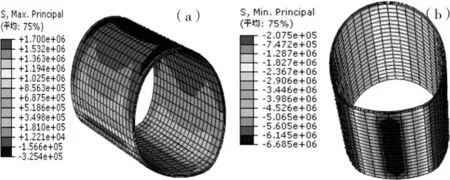
(a) 拉應力;(b) 壓應力圖11　動靜荷載耦合作用下新黃土隧道初支應力云圖Fig.11 Coupled stress contour of initial support after

結果分析表明：1)相比于重載列車作用對結構產生的應力，圍巖應力釋放對結構所產生的應力貢獻更大。2)二次襯砌與初期支護的最不利位置為仰拱與邊墻連接處及仰拱中心位置，二次襯砌仰拱中心及初期支護連接處兩部位的拉應力較大，二次襯砌仰拱與邊墻連接處及初期支護仰拱中心分別為兩者的壓應力最大位置。

綜合上述分析可見，二次襯砌仰拱中心及初期支護邊墻與仰拱連接處兩者的拉應力水平較大(圖13)，為隧道結構的疲勞關鍵位置，二次襯砌及初期支護的壓應力水平相較于其抗壓強度小，遠小于0.5ft，非結構疲勞破壞控制因素，壓應力水平不會產生疲勞問題。

3隧底結構疲勞壽命及疲勞極限

強度

由上述分析可知，列車轉向架通過時引起的應力最大，而隧道疲勞壽命主要是受大幅值應力循環的影響，小的應力波動無規律且對疲勞壽命影響很小，可以忽略，因此，可將列車轉向架通過時的應力時程曲線簡化為3種主要的應力循環，采用雨流計數原理對其進行統計，應力循環統計簡化如圖14。從中可得，每個轉向架通過，即每節車廂通過時，最大應力循環為1個(1-2-7)，列車車輪通過時達最大拉應力，靜力狀態下為最小拉應力值。次級應力循環1個(4-5-6)，為每個輪對通過時引起的應力循環。低應力循環為2個(2-3-4)，為同一輪對兩相鄰車輪通過時引起的應力循環。

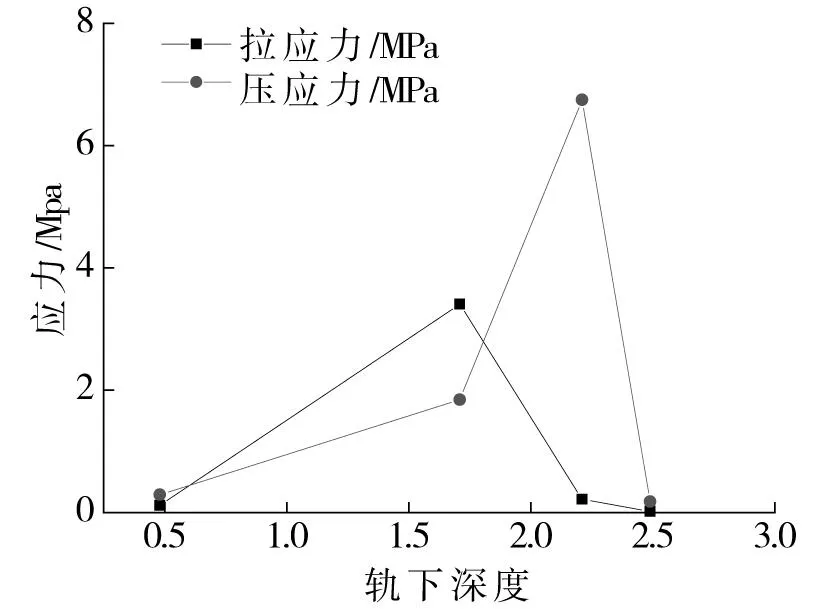
圖12　隧底耦合應力沿軌下深度變化曲線Fig.12 Coupled stress of bottom structures under the rail

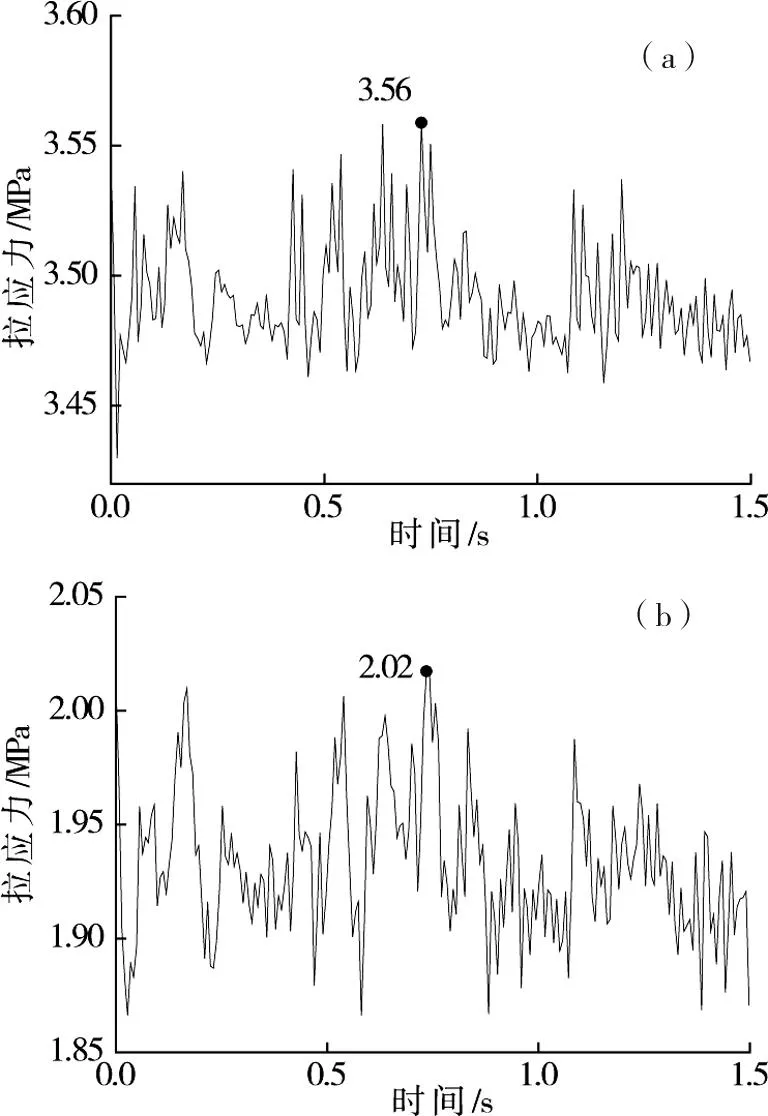
(a)二襯隧底中心;(b)初支連接處圖13　隧底結構最大拉應力時程曲線Fig.13 Maximum tensile stress time-history curves of bottom structures in tunnel

軸重30 t煤炭重載敞車每節車廂載重97 t，每列206節車廂，于是可統計得到一列2萬t列車通過時將產生1次大應力循環，207次中應力循環和412次低應力循環。

圖14　應力循環簡化圖形Fig.14 Simplify counting figue of stress cycle

由此，可根據動力響應結果及疲勞壽命計算理論得到St,max和ΔSt等參數，代入S-N曲線公式可分別計算各處應力水平達到疲勞破壞時的應力循環次數Ni，如表2。同樣已知容許的應力循環次數，也可求出相應的疲勞上限強度σfu，即初期支護C25噴射混凝土、二次襯砌仰拱C35混凝土對應的受拉疲勞上限強度分別為1.30和1.62 MPa。

表2　疲勞破壞時的應力循環次數

而根據第3節的計算結果，二次襯砌仰拱中心處拉應力最大為3.56 MPa，初期支護仰拱與邊墻連接處最大拉應力為2.02 MPa，均超過抗拉疲勞上限強度，無法滿足長期運營要求，須采取加固措施。

4重載鐵路隧道適應性強化

當前關于隧底強化措施主要有系統錨桿注漿和地基處理(土擠密樁、灰土擠密樁)。本文對上述2種措施分別建立數值模型，探討經強化處理后的隧道結構動力響應及疲勞壽命情況，以評價對應強化措施的有效性。

系統錨桿注漿加固后土體參數參照文獻[14-15]選取。地基處理(土擠密樁加固)后的地層參數可按E=mEp+(1-m)Es計算[16]，式中，E為復合地基彈性模量；Ep為擠密樁彈性模量；Es為土體彈性模量;m為置換率。強化后的數值計算模型如圖15。

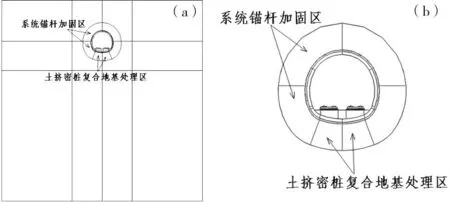
(a) 整體加固模型;(b) 加固處理區圖15　加固模型Fig.15 Strengthening model

4.1單一系統錨桿強化后的計算結果分析

圖16～17分別為系統錨桿加固長度取3及5 m時，二次襯砌仰拱中心及初期支護仰拱與邊墻連接處等疲勞關鍵部位的應力時程曲線。從中分析可見：

1)隧底結構疲勞關鍵部位的應力峰值數據較無強化措施時有較大程度的減小，錨桿加固長度分別為3和5 m時，二次襯砌仰拱中心最大拉應力值比無強化措施時減小20.6%和28.5%，初期支護仰拱與邊墻連接處分別減小32.5%和36.9%。2)強化后，相應部位最大拉應力值統計于表3，系統錨桿長度為3 m時，應力減小為1.36 MPa，仍大于受拉疲勞上限強度；而長度達5 m時，初期支護最大拉應力減小為1.27 MPa，小于疲勞上限強度，二次襯砌仰拱中心部位的最大拉應力仍有2.54 MPa，無法滿足二次襯砌疲勞壽命要求，可見采用單一系統錨桿注漿對隧底結構應力水平減小有限。

表3系統錨桿注漿后隧底結構拉應力最大值

Table 3Maximum tensile stress of bottom structures after system anchoring bolt grouting

MPa

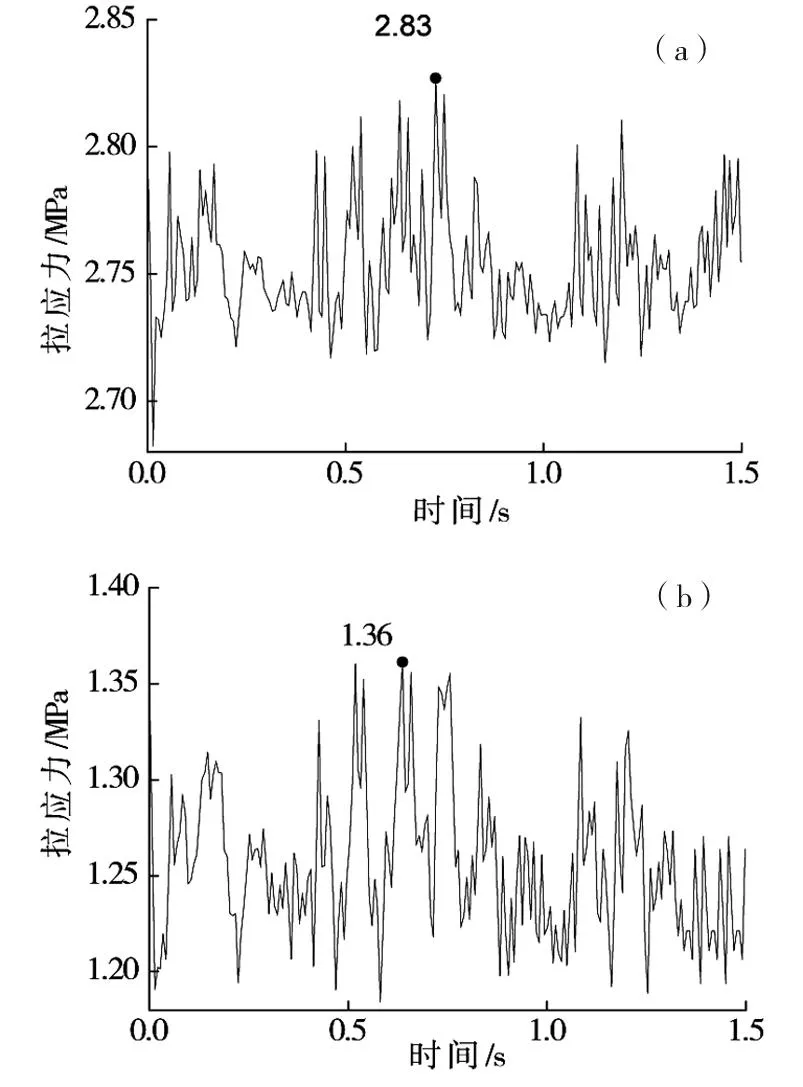
(a) 二襯仰拱隧中；(b) 初支連接處圖16　錨桿注漿3 m時隧底結構應力時程曲線Fig.16 Stress time-history curves of buttom structures when the length of system anchoring bolt is 3 m

(a)二襯仰拱隧中；(b)初支連接處圖17　錨桿注漿5 m時隧底結構應力時程曲線Fig.17 Stress time-history curves of buttom structures when the length of system anchoring bolt is 5 m

4.2系統錨桿和地基處理聯合強化后計算結果

分析

以系統錨桿加固長度3 m為基礎，地基處理深度分別取3和4 m，得到二次襯砌仰拱中心及初期支護仰拱與邊墻連接處等疲勞關鍵部位的應力時程曲線如圖18～19。

從中分析可知：1)經復合強化處理后，隧底結構疲勞關鍵部位的應力峰值數據較不加固時有顯著的降低，基底加固深度分別為3和4 m時，二次襯砌仰拱中心最大拉應力值比不加固時減小49.1%和56.4%，初期支護仰拱與邊墻連接處分別減小59.8%和61.2%。2)進一步提取隧底結構的最大拉應力值如表4，從中可見，系統錨桿注漿加固同時采用基底處理區域長度為4 m時二次襯砌仰拱中心、初期支護仰拱與邊墻連接處應力水平均小于受拉疲勞上限強度，此時在軸重30 t重載列車作用下，黃土隧道結構能滿足100 a設計壽命期內服役性能的要求。

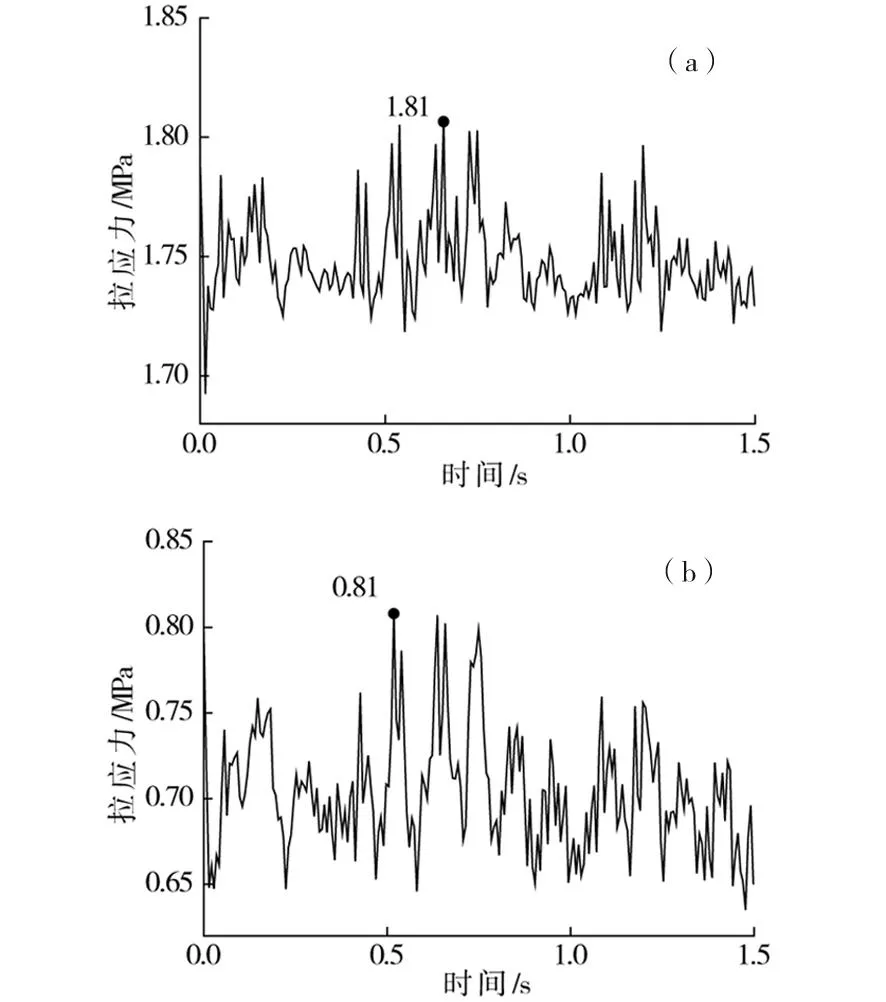
(a)二襯仰拱隧中;(b)初支連接處圖18　錨桿注漿與地基處理半徑為3 m時隧底結構拉應力時程曲線Fig.18 Stress time-history curves of bottom structures when the length of system anchoring bolt combined with ground treatment is 3 m

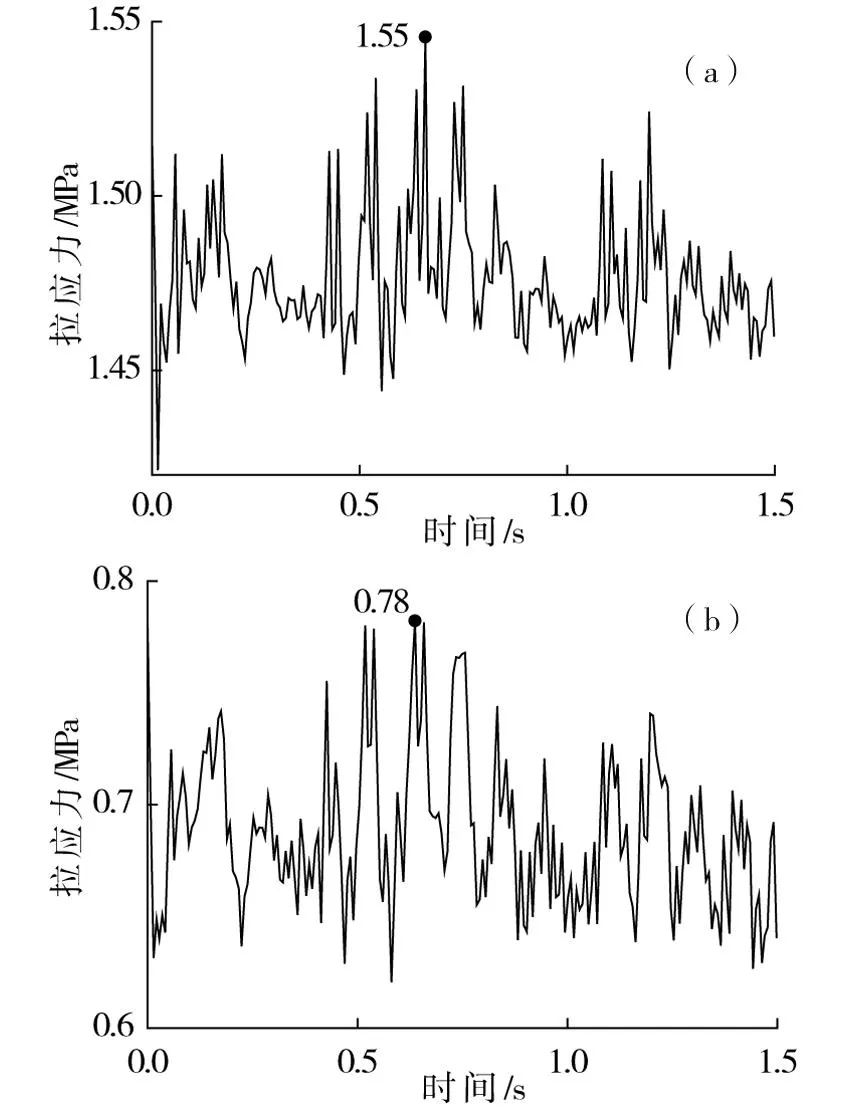
(a)二襯仰拱隧中;(b)初支連接處圖19　錨桿注漿與地基處理半徑為4 m時隧底結構拉應力時程曲線Fig.19 Stress time-history curves of bottom structures when the length of system anchoring bolt combined with ground treatment is 4 m

Table 4 Maximum tensile stress of bottom structures after ground treatment

MPa

5結論

1)軸重30 t重載列車作用下，隧底結構動拉應力隨深度先增大后減小，在二次襯砌仰拱中達到峰值，初期支護中拉應力次之，隨后迅速衰減；動壓應力在填充層頂面最大并隨深度呈線性減小。

2)圍巖應力與列車荷載耦合作用下，隧底結構拉壓應力均先隨軌下深度先增大后減小；隧底結構拉應力在二次襯砌仰拱中達到最大，壓應力初期支護中達到最大，其中二次襯砌仰拱中心與初期支護仰拱與邊墻連接處兩者為疲勞損傷的最不利位置，且不能滿足重載列車長期安全運營的要求。

3)根據重載鐵路年運量、使用年限及疲勞壽命分析理論，可得新黃土隧道在30 t軸重荷載作用下，初期支護C25噴射混凝土、二次襯砌仰拱C35混凝土受拉疲勞上限強度分別為1.30和1.62 MPa。

4)單一的系統錨桿注漿加固對隧底結構應力水平降低的作用有限，錨桿長度達5 m時仍無法滿足軸重30 t重載列車運行的適應性要求；而當采用系統錨桿加固和地基處理，基底應力水平的降低顯著，處理深度達4 m時，可滿足軸重30 t重載鐵路新黃土隧道100 a設計運營期內服役性能的要求。

參考文獻：

[1] 牛亞彬. 重載鐵路隧道病害機理及整治技術研究[D]. 北京: 中國鐵道科學研究院, 2013.

NIU Yabin. The heavy haul railway tunnel diseases mechanism and remediation technology research [D]. Beijing: China Academy of Railway Sciences, 2013.

[2] 馮冀蒙, 仇文革, 王玉鎖, 等. 既有隧道病害分布規律及圍巖環境等級劃分研究[J]. 現代隧道技術,2013, 50(4): 35-41.

FENG Jimen, QIU Wenge, WANGYusuo, et al. Study of defect distribution regularity in existing tunnels and the classification of tunnel environments[J]. Modern Tunnelling Technology, 2013, 50(4): 35-41.

[3] 王秀英, 龔增進, 劉維寧. 30 t軸重條件下隧道技術標準研究[J]. 鐵道工程學報, 2009, 128(5): 54-58.

WANG Xiuying, GONG Zengjin, LIU Weining. Research on the tunnel technical standard under 30t axis load [J]. Journal of Railway Engineering Society, 2009, 128(5): 54-58.

[4] 付兵先, 馬偉斌. 重載列車作用下隧道基底荷載特征及動力學響應分析[J]. 鐵道建筑技術, 2013(8): 1-5.

FU Bingxian, MA Weibin. Base load characteristics and dynamic response analysis of tunnel under heavy haul train[J]. Railway Construction Technology, 2013 (8): 1-5.[5] 黃娟. 基于損傷理論的高速鐵路隧道結構振動響應分析及疲勞壽命研究[D]. 長沙: 中南大學, 2010.

HUANG Juan. Study on the vibration response and fatigue life of high- speed railway tunnels based on damage theory [D]. Changsha: Central South University, 2010.[6] LEI Mingfeng, OMER Joshua. Study on train vibration response and cumulative deformation of double arch tunnel in Kast foundation [J]. Geotechnical and Geological Engineering, 2015, 33(3): 549-558.

[7] 晏偉光. 重載鐵路隧底結構動力響應及疲勞壽命研究[D]. 長沙: 中南大學, 2013.

YAN Weiguang. Research on dynamic response and fatigue life in bottom structure of heavy haul railway tunnel [D]. Changsha: Central South University, 2013.

[8] 徐新利. 30 t軸重重載列車作用下隧底脫空對基底結構受力的影響[J]. 鐵道建筑，2015(4): 44-49.

XU Xinli. Influence of separation from tunnel's bottom on bearing capacity of base structure under train loading of 30 t axle load [J]. Railway Engineering, 2015 (4): 44-49.

[9] 薛繼連. 30t軸重下隧底密實度對隧底結構受力的影響及隧底加固效果分析[J]. 中國鐵道科學, 2015, 36(1): 90-95.

XUE Jilian. Analysis of the influence of tunnel bottom compactness on structure stress and strengthening measures under 30t axle load train [J]. China Railway Science, 2015, 36(1): 90-95.

[10] 丁祖德, 杜永剛, 彭立敏, 等. 基底圍巖性狀對高速鐵路隧道結構動力響應的影響分析[J]. 現代隧道技術, 2015, 52(3): 88-94.

DING Zude, DU Yonggang, PENG Limin, et al. Influence of tunnel base rock mass properties on the dynamic response of high-speed railway tunnels[J]. Modern Tunnelling Technology, 2015, 52(3): 88-94.

[11] 梁波, 蔡英. 不平順條件下鐵路路基的動力分析[J]. 鐵道學報, 1999, 21(2): 84-88.

LIANG Bo, CAI Ying. Dynamic analysis on subgrade of high speed railways in geometric irregular condition[J]. Journal of the China Railway Society, 1999, 21(2): 84-88.

[12] GB 50010—2010， 混凝土結構設計規范[S].

GB 50010—2010， Code for design of concrete structrues[S].

[13] CEB-FIP Model Code 2010, First Complete Draft [S]. Switzerland: Thomas Telford Services Ltd, 2010.

[14] 雷進生. 碎石土地基注漿加固力學行為研究[D]. 武漢: 中國地質大學, 2013.

LEI Jinsheng. Research on mechanical behavior of grout in gravelly soil foundations[D]. Wuhan: China University of Geosciences, 2013.

[15] 秦愛芳, 李永圃, 陳有亮. 上海地區基坑工程中的土體注漿加固研究[J]. 土木工程學報, 2000, 33(1): 69-72,82.

QIN Aifang, LI Yongpu, CHEN Youliang. Study on stabilizing grout of excavation pits in Shanghai district[J]. China Civil Engineering Journal, 2000, 33(1): 69-72,82.

[16] JGJ79—2012,建筑地基處理技術規范[S].

JGJ79—2012, Technical code for ground treatment of buildings[S].

Adaptability and strengthening research of 30 t axle heavy haul railway tunnel in new loess areaLIU Cong, PENG Limin, LEI Mingfeng, SHI Chenghua

(School of Civil Engineering, Central South University, Changsha 410075, China)

Abstract：Based on the typical tunnel structure of Menghua railway which is still under construction, a numerical study was performed, mainly focusing on the dynamic response, fatigue life and strengthening measures of loess heavy haul railway tunnel. The results show that: with an increase of axle load and railway freight transport volume, the existing railway tunnel cannot meet the long-term safety requirement without strengthening measures. The adaptability of loess heavy haul railway tunnel cannot be improved effectively by using sole systematic bolt, system anchoring bolt combined with ground treatment should be adopted (the length should reach to 4 m or more). Then the safety operation requirement of the heavy haul train can be satisfied. The research indicates that the centre of secondary lining of inverted arch, and sidewall and inverted arch joint of initial support are the most unfavorable load positions of the tunnel’s bottom structures under the action of 30 t axle heavy haul train. In order to satisfy the 100 a safety design service life of tunnel structures under the operation of 30 t axle heavy haul train, the upper-limit fatigue strength of initial and secondary lining of new loess tunnel were deduced, which are 1.30 MPa and 1.62 MPa, respectively. The results can provide reference for present design of heavy haul tunnel structures.

Key words：30 t axle; heavy haul railway tunnel; adaptability; fatigue life; strengthening measurements

中圖分類號：U 25

文獻標志碼：A

文章編號：1672-7029(2016)04-0730-10

通訊作者：雷明鋒(1982-)，男，湖南祁東人，博士，講師，從事隧道與地下工程方面的教學與科研工作；E-mail:124520238@qq.com

基金項目：國家自然科學基金資助項目(U1361204，51278494)；湖南省創新平臺與科技人才項目(2015RS4006)

收稿日期：2016-02-02