基于模糊失效準則的橋梁易損性分析方法

蔣崇文，易偉建，龐于濤

(1.湖南大學 土木工程學院，湖南 長沙 410000；2.中國地質大學(武漢) 工程學院，湖北 武漢 430070)

?

基于模糊失效準則的橋梁易損性分析方法

蔣崇文1，易偉建1，龐于濤2

(1.湖南大學 土木工程學院，湖南 長沙 410000；2.中國地質大學(武漢) 工程學院，湖北 武漢 430070)

摘要:目前，大多數易損性分析方法采用的損傷等級的取值都是確定的，然而，在實際的工程中，結構損傷域的邊界不明確，具有一定的模糊性。為此，本文在傳統易損性分析的基礎上，結合模糊數學與傳統可靠度計算方法，考慮模糊準則下的結構易損性。并以一座單塔斜拉橋為例，建立結構的概率地震需求模型，分析考慮模糊準則與不考慮模糊準則2種情況下，4個關鍵部位的易損性曲線。研究結果表明：在考慮模糊準則與不考慮模糊準則2種情況下的結構的地震易損概率明顯不同，因而，有必要在地震風險評估中考慮模糊失效準則的影響。

關鍵詞：模糊失效準則；地震易損性；斜拉橋；可靠度

在橋梁結構的地震損傷分析中，經常伴有很多不確定性因素，主要包括地震本身的不確定性與結構本身的不確定性。關于這2部分的不確定性對結構的影響，已經得到國內外研究的重視。就目前總的研究趨勢來看，主要的難點還在于如何更好地考慮不確定性因素以及減少相應的計算量[1-3]。從隨機統計學科的角度而言，不確定性主要有2種：隨機性和模糊性。隨機性是指結構實測信息不夠充分而導致的結果誤差[4-5]。模糊性是指由于排中律的缺失，結果本身并沒有明確的界限。在系統與體系失效領域中，模糊性經常表現為失效模式的多樣化，而結構損傷領域，模糊性經常體現為損傷等級的漸變以及損傷等級的重疊。對于結構損傷分析而言，所給定的損傷指標的取值往往固定，代表了結構從非破壞狀態到破壞狀態，輕微破壞狀態到嚴重破壞狀態的突變，這與實際情況往往是不相符的，在實際中結構的損傷與損傷等級的取值表現為漸變的過程，在這種情況下，結構損傷域的邊界其實是不明確的。目前的研究也大多集中考慮結構的隨機性和荷載的隨機性的影響，而對于模糊性的研究并不多見。由于目前結構的損傷分析一般以易損性曲線的形式表達，本文引入模糊隨機理論，用隸屬函數來簡化考慮損傷邊界的漸變性，并結合經典可靠度的理論方法，推導相應的模糊失效準則，并以一座單塔斜拉橋為例，進行了易損性分析，并與傳統的易損性曲線進行了對比，得到了一些有意義的結果。

1模糊失效準則

對于功能函數Z=g(X)，且失效域為{x|gX(x)≤0}，那么經典可靠度理論求解的失效概率為

(1)

(2)

(3)

模糊隨機事件的概率為其隸屬函數的數學期望。

在結構易損性分析中，失效準則的模糊性使功能函數Z=g(X)的值具有模糊性。設結構失效模糊隨機事件可表示為

(4)

設Z的概率密度函數為fZ(z)，根據式(3)，結構的失效概率為

(5)

設基本隨機變量X的聯合概率密度函數為fX(x)，結構失效概率可表達為

(6)

直接進行式(6)的多重積分的計算通常是有困難的，本文采取下列的處理方法，這種方法類似于一次二階矩方法中的映射變換法[8]。

(7)

式中，新的隨機變量K的累積分布函數和概率密度函數分別為

(8)

(9)

根據式(7)，基于模糊失效準則的隨機可靠度問題的失效域為{x|gX(x)≤k}，對于易損性損傷準則而言，判斷一個構件的失效與否的功能函數為

(11)

式中：D為地震作用下結構的需求；C為地震作用下結構的能力；ri根據各個損傷等級不同來取值。根據前文所陳述的方法，式(11)的功能函數轉化為

(12)

對于式(12)，可用傳統可靠度方法計算失效概率[6-7]，本文采用蒙特卡洛方法來進行計算。

2算例

2.1模型描述

本文所選某座獨塔雙索面斜拉橋，跨徑布置為150+125 m。主梁為工字鋼和混凝土板的組合梁，主塔為A形鋼筋混凝土塔。橋塔全部采用C30混凝土，縱向鋼筋采用二級鋼筋。圖1為結構的非線性有限元模型及關鍵截面配筋情況。斜拉橋的非線性有限元模型采用OpenSees[9]程序建立，主梁以及主塔橫梁采用彈性梁柱單元模擬，墩柱與主塔采用非線性梁柱單元模擬，圖1給出了關鍵截面的纖維劃分與OpenSees模擬的彎矩-曲率曲線。在非線性梁柱單元的纖維截面中，核心混凝土與保護層混凝土都采用了concrete01模型[10-11]，且均不考慮混凝土的抗拉性能。鋼筋采用steel01雙線性滯回模型，有限元模型采用集中質量矩陣。選取的3類場地共56條地震波，地震持時均為30 s，圖2為56條波阻尼為5%的偽加速度反應譜曲線，黑色粗線代表平均線[12]。另外，本文并沒有考慮樁土相互作用，墩底采用了固結的形式。

圖1　結構的非線性有限元模型Fig.1 Non-linear finite element model of the structure

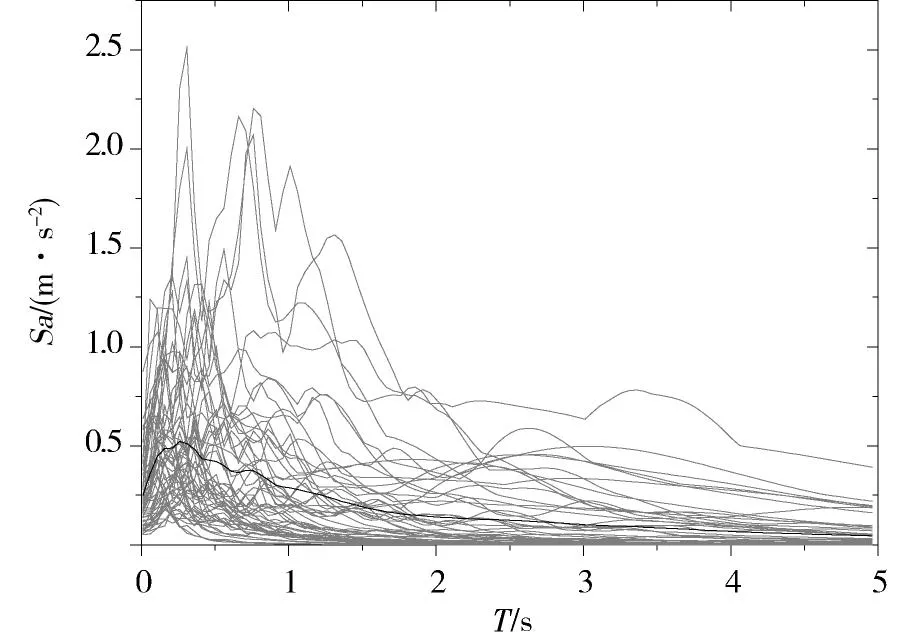
圖2　60條波的偽加速度反應譜曲線Fig.2 Pseudo-acceleration response spectrum of the 56 wave curve

2.2基于云圖法的地震易損性分析

對于地震易損性而言，有2種主要方法，一種采用云圖法進行非線性時程分析，并根據冪指數法則對地震需求結果進行擬合，得到概率需求模型，并與構件能力一起通過經典可靠度理論計算得到構件的失效概率[10]，另外一種方法是IDA方法，對所用的地震波進行放縮，并在相應的地震動參數上進行概率分布函數擬合，通過蒙特卡洛方法得到結構的失效概率。在本文云圖法的計算中，地震易損性分析計算包括2部分：計算結構的概率地震需求以及建立地震易損性曲線。在地震需求計算部分，結合非線性時程分析方法，通過收集的60條地震波，建立在地震作用下的結構概率地震需求模型PSDM。圖3為斜拉橋的幾個關鍵部位的概率地震需求模型(關鍵部位由圖1給出)。表1為PSDM中的擬合曲線與相應的方差。而在建立易損性曲線的過程中，需要定義結構損傷的衡量指標。本文參考HAZUS-MH MR3關于結構性能的劃分標準如下所示：1)輕微損傷；2)中等損傷；3)嚴重損傷；4)倒塌；本文使用結構曲率延性系數φε來定義損傷階段[8-9]，曲率延性系數φε取為地震反應下的結構曲率與首次屈服曲率的比值。

2.3模糊失效準則

在易損性分析中，判斷結構構件或關鍵截面的損傷的功能函數可表示為

Zi=ri-φε

(13)

上文所闡述4個損傷等級(輕微損傷；中等損傷；嚴重損傷；倒塌)定性描述為，鋼筋屈服，核心混凝土到達峰值強度，混凝土保護層退出工作，核心混凝土到達極限應變。根據這些定性描述，進行截面的彎矩曲率分析，計算得到其相應的曲率延性系數。將這些系數與相應的文獻進行比較[5-6]，最后確定ri取值分別為1.0，2.0，4.0和7.0，i對應4個損傷等級。結構單元的損傷域為Z≤0。引入模糊準則以后，判斷各個單元損傷的功能函數為

Zi=ri-φε-K

(14)

(a)塔中橫梁處截面；(b)塔底截面；(c)左岸截面；(d)右岸截面圖3　斜拉橋的幾個關鍵部位的概率地震需求模型(關鍵部位由圖1給出)Fig.3 Probability of several key parts of the cable-stayed bridge seismic demand model

響應位置PSDM方差ln(φε)G10.9377*ln(PGA)-8.59310.51232ln(φε)G20.8544*ln(PGA)-8.95470.83335ln(φε)G31.2435*ln(PGA)-6.24620.52306ln(φε)G41.2704*ln(PGA)-6.21130.55621

(15)

式中，γ表征了模糊性的大小。當γ取0.5時，本文比較了式(14)的計算與式(6)的多重積分的計算結果，如圖4(a)所示。從圖4(a)可以看出，式(14)與式(6)的多重積分的計算結果擬合較好，說明了式(14)的推導正確，并且說明了本文簡化算法的準確性。從圖4(b)可以看出，不同γ值可能導致地震易損概率的不同。由于γ值跟損傷邊界所表征的模糊性有關，因而γ值的確定需要試驗數據的支撐，在本文中，γ值取為適中的0.5[13-15]。之后采用式(14)即可計算失效概率。

本文使用Monte Carlo法來計算結構的失效概率，從而形成易損性曲線。具體過程如下：采用表1中的PSDM模型，得到不同PGA下的響應的對數正態分布參數，并使用Matlab中的隨機數生成程序來生成隨機數，代入式(14)中進行比較(當然，K也是隨機變量，需要進行隨機數的生成)，如果功能函數的值小于0，那么說明結構需求大于能力，最后進行統計功能函數小于0的數量，這個數量除于樣本總數就是結構的失效概率，例如，在計算中，使用了1 000個樣本，而式(14)小于0的數量為100個，那么失效概率為100/1 000=0.1。圖5為考慮模糊準則與不考慮模糊準則2種情況下，4個關鍵部位的易損性曲線。

從圖5可以看出，當地震需求參數取為結構截面曲率時，不考慮模糊準則的結構地震易損超越概率要大于考慮模糊準則的易損超越概率，這可能是由于在模糊損傷準則的條件下，本來已經損傷的樣本數據在模糊定義下并不損傷。這也說明，不考慮損傷邊界模糊性的地震易損性分析可能會高估結構在地震動作用下發生某一損傷等級的超越概率，從而在地震風險評估中得到過高的地震風險，從而提高了結構的應有的性能水準。因而在進行結構的地震易損性分析時，有必要考慮模糊失效準則對易損性的影響。

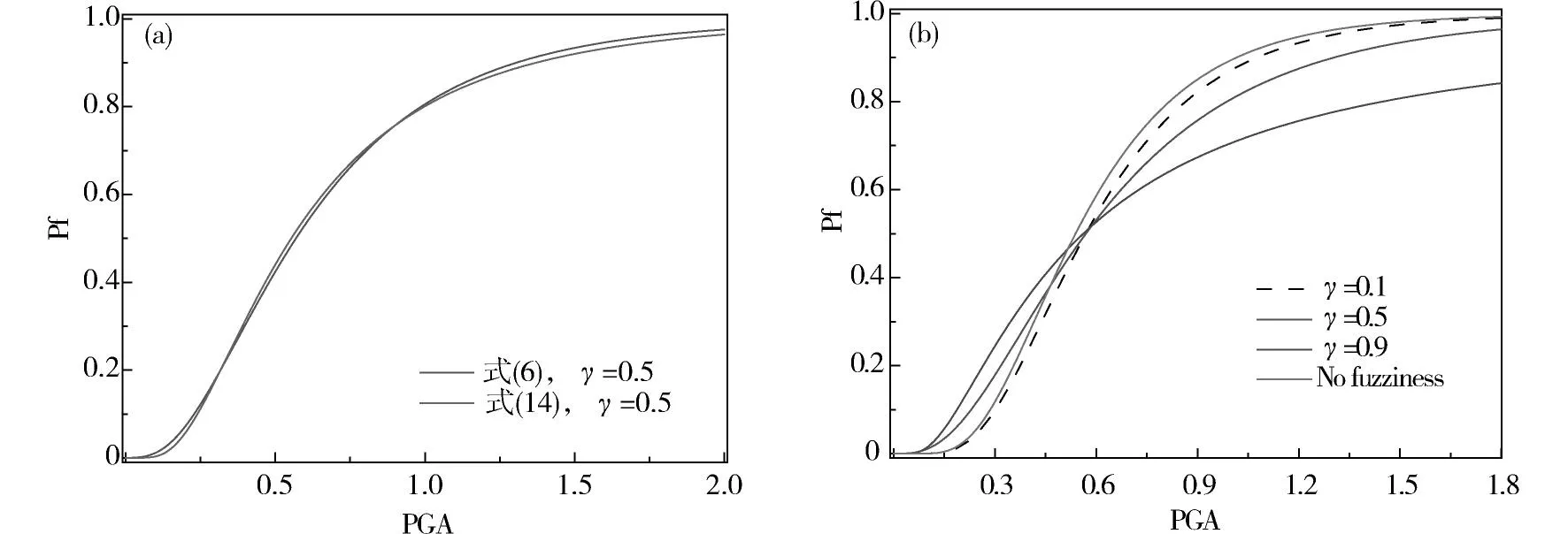
(a)式(14)與式(6)的對比；(b) 不同γ值的影響圖4　模糊失效準則計算模式以及參數γ的影響Fig.4 Fuzzy-stochastic calculation model and the impact of the parameterγ

(a)輕微損傷；(b)中等損傷；(c)嚴重損傷；(d)破壞圖5　考慮模糊準則與不考慮模糊準則2種情況下，4個關鍵部位在4個不同損傷等級下的易損性曲線Fig.5 Fragility curves of four key parts at different levels of damage

3結論

1)模糊準則可以通過在功能函數中引入隨機變量的簡化方式實現，這種方式與多重積分方法的計算結果沒有差距。

2)不考慮模糊準則來進行結構的易損性分析，可能會高估結構的潛在地震危險，且這種影響與模糊性的大小有關，因此有必要在易損性分析中考慮模糊準則對結構失效概率的影響。

參考文獻：

[1] H Hwang, 劉晶波.地震作用下鋼筋混凝土橋梁結構易損性分析[J].土木工程學報，2004，37(6)：47-51.

H Hwang, LIU Jingbo. Seismic fragility analysis of reinforced concrete bridge[J]. China Civil Engineering Journal, 2004,37(6):47-51.

[2] Shinozuka M, Feng M Q, Lee J-H, et .a1. Statistical analysis of fragility curve[J]. Journal of Engineering Mechanics, ASCE, 2000，126 (12):1224-1231.

[3] Karim K R, Yamazaki F. Effect of earthquake ground motions on fragility curves of Highway Bridge piers based on numerical simulation[J]. Earthquake Engineering and Structural Dynamics, 2001, 30(12):1839-1856.

[4] Hwang H H M, Huo J-R. Probabilistic seismic damage assessment of highway bridges[C]// The 6th U.S. National Conference on Earthquake Engineering, Seattle, Washington, June, 1998.

[5] Choi D E, DesRoches R, Nielson B. Seismic fragility of typical bridges in moderate seismic zones[J]. Eng Struct, 2004, 26(2): 187-199.

[6] Yang C S, DesRoches R, Padgett J E. Fragility curves for a typical California box girder bridge[C]// TCLEE 2009: Lifeline Earthquake Engineering in a Multihazard Environment, ASCE, Reston, VA, 2009: 1-12.

[7] 馮清海.特大橋梁地震易損性與地震風險概率分析[D].上海：同濟大學，2008.

FENG Qinghai. The seismic vulnerability and risk probability of super-large bridge[D]. Shanghai: Tongji University, 2008.

[8] 趙國藩,金偉良,貢金鑫.結構可靠度理論[M].北京:中國建筑工業出版社, 2001.ZHAO Guofan, JIN Weiliang, GONG Jinxin. Structural reliability theory[M]. Beijing: China Architecture&Building Press, 2001.

[9] Mazzoni S, Mckenna F. OpenSees Command Language Manual[M]. 2006.

[10] 姜沖虎,楊博聞,李德建,等.獨塔斜拉橋抗震分析及其合理約束體系研究[J].鐵道科學與工程學報, 2014, 11(6)：6-12.

JIANG Chonghu, YANG Bowen, LI Dejian, et al. Seismic analysis and its restraint system feasibility of single pylon cable-stayed bridge[J]. Journal of Railway Science and Engineering, 2014, 11(6):6-12.

[11] Scott B D, Park P, Priestley M J N. Stress-strain behavior of concrete confined by overlapping hoops at low and high-strain rates[J]. J Am Concr Inst, 1982, 79(1):13-27.

[12] 鄭永陽,扶名福.抗震設計反應譜統一計算方法及譜兼容地震波[J].鐵道科學與工程學報, 2014, 11(6)：38-44.

ZHENG Yongyang, FU Mingfu. Unified calculation method of design response spectrum and generation of synthetic earthquake accelerograms compatible with the spectrum[J]. Journal of Railway Science and Engineering, 2014, 11(6):38-44.

[13] Bazzurro P, Comee C A. Seismic hazard analysis for non-linear structures. Ι Methodology[J]. ASCE Journal of Structural Engineering，1994b,120(II)：3345-3365.

[14] 胡聿賢．地震工程學[M]．2版．北京：地震出版社，2006.

HU Yuxian．Earthquake engineering[M]．2nd edition．Beijing：China Earthquake Press，2006.

[15] 蔣麗忠，吳忠河，王臣．框架結構彈性及彈塑性反應譜研究[J]．鐵道科學與工程學報，2009，27(1)：6-9．

JIANG Lizhong，WU Zhonghe，WANG Chen．Elastic reaction and elastoplastieity spectrum of composite steelconcrete frame[J]．Journal of Railway Science and Engineering，2009，27(1)：6-9．

Seismic fragility analysis of bridges using fuzzy-stochastic methodJING Chongwen1, YI Weijian1, PANG Yutao2

(1．College of Civil Engineering, Hunan University, Changsha 410081, China；2.College of Engineering, China University of Geosciences, Wuhan 430070, China)

Abstract:At present, the value of different damage levels is costant in most fragility analysis. However, in actual projects, the boundary of structural damage domains is actually not explicit, and have the characteristic of fuzziness. Therefore, this paper proposes a fuzzy-stochastic method to analyze seismic vulnerabilities of highway bridges on the basis of traditional fragility theory. The fuzzy-stochastic method combines the fuzzy mathematics and the traditional reliability method. The details of this method are illustrated by taking a single pylon cable-stayed bridge as an example. The probabilistic seismic demand model is established to calculate the probability of bridge components, and fragility curves of four key sections in two different cases of are compared to study the influence of the fuzzy rules on the fragility curves. It is found that the fuzzy rules has a significant influence on structure vulnerabilitis and should be taken into account in the potential earthquakes risk assessment.

Key words:fuzzy-stochastic method; seismic fragility analysis; highway gridge; reliability

中圖分類號：P315.9

文獻標志碼：A

文章編號：1672-7029(2016)04-0705-06

通訊作者：易偉建(1954-)，男，湖南黔陽人，教授，從事橋梁抗震方面的研究；E-mail: wjyi@hnu.cn

基金項目：國家自然科學基金資助項目(51578228)

收稿日期：2015-11-29