時速250 km/h鐵路雙線箱梁的畸變效應研究

藺鵬臻，孫理想，冀偉，楊子江

(蘭州交通大學 甘肅省道路橋梁與地下工程重點實驗室，甘肅 蘭州 730070)

?

時速250 km/h鐵路雙線箱梁的畸變效應研究

藺鵬臻，孫理想，冀偉，楊子江

(蘭州交通大學 甘肅省道路橋梁與地下工程重點實驗室，甘肅 蘭州 730070)

摘要:為了分析時速250km/h鐵路32m跨度雙線標準箱梁的畸變效應，基于板殼有限元建立了畸變效應分析的數值模型。采用板殼有限元方法和傳統解析方法，對比計算僅單線活載作用下的畸變應力分布規律。通過定義翹曲比例系數，研究高跨比、寬跨比和壁厚等設計參數對畸變應力的影響規律。研究結果表明:與傳統解析解比較，板殼有限元法更適合于箱梁畸變效應的分析。單線活載偏心作用下，跨中截面箱梁頂板靠近翼緣板邊緣部位的翹曲比例系數可達11.6%；腹板與底板相交處翹曲比例系數最大，可達13.9%。跨中和l/4截面的翹曲比例系數ξ分析表明，現有箱梁設計參數合理，跨中最大翹曲比例系數小于15%，而l/4截面基本為0。箱梁高跨比、寬高比、壁厚等設計參數對畸變效應均有一定影響，總體規律是畸變效應隨高跨比、寬高比和壁厚的增大而減小。

關鍵詞：鐵路箱梁；畸變；翹曲應力；數值分析

客運專線鐵路與我國既有鐵路相比, 具有速度高、對線路平順性要求高等特點, 要求其橋跨結構具有較大的抗彎和抗扭剛度, 整孔雙線簡支箱梁由于受力簡單、明確、形式簡潔、外形美觀、抗扭剛度大，建成后的橋梁養護工作量小以及噪音小等優點, 在許多國家的高速鐵路建設中得到了廣泛應用[1-2]。對雙線鐵路箱梁而言，當僅有單線運行列車時，列車活載相當于箱梁整體縱軸線的偏心荷載，將引起橋梁的扭轉和畸變[1-2]。目前國內現有設計規范中[3-4]，基于箱壁較厚或橫隔板較密的前提假設，認為箱梁畸變應力所占比例較小，設計中忽略畸變應力計算。但隨著橋梁建設中雙線鐵路箱梁的出現、僅在梁端設置橫隔板以簡化構造和方便施工等趨勢的發展，箱梁畸變產生的條件發生了變化，需要分析新時期箱梁結構的畸變效應規律。對于箱形梁畸變的分析，常用的方法有解析法和有限元法2種[1]。解析法將作用于箱形梁截面上的偏心荷載根據等效荷載思想分解成對稱荷載與反對稱荷載，對稱荷載作用時按梁的彎曲理論求解；反對稱荷載作用時根據薄壁桿件扭轉理論分解為剛性扭轉和畸變兩種荷載模式的疊加[5]。畸變應力的解析計算方法，較為常見的分析方法有基于彈性地基梁的比擬法[6-7]和廣義坐標法[8]。解析法通常首先確定畸變荷載，進而根據解析方程求得畸變引起的縱向翹曲正應力、剪應力和橫向彎曲應力，計算過程較為繁瑣。有限單元法基于三維板殼和塊體理論，建立箱梁結構精細的三維有限元數值分析模型，施加箱梁邊界和畸變荷載，求解獲得畸變應力，是當前結構精細化分析的通用和便捷方法。Ghani等[9]應用板殼有限元模型，研究了橫隔板和幾何特征對鋼箱梁畸變效應的影響。本文以時速250 km/h客運專線32 m標準跨度雙線簡支梁為研究對象，通過有板殼限元法數值模擬，研究箱梁的畸變效應。

1畸變效應分析模型

1.1箱梁基本參數

時速250 km/h客運專線32 m標準跨度簡支箱梁跨中截面如圖1所示。橋梁設計標準為雙線，線間距4.6 m。軌道結構采用雙塊式無砟軌道，橋面板上直接鋪設無砟軌道底座板。活載縱向采用ZK標準活載。梁體為C50混凝土，彈性模量按規范取值E=3.55×104MPa。

單位:cm圖1　箱梁跨中截面Fig.1 Box girder section of mid-span

1.2有限單元模型

數值分析模型采用ANSYS軟件SHELL63板殼單元模擬混凝土箱梁。由于本文主要分析箱梁彈性階段的畸變效應，因此建模不考慮鋼筋的影響。有限元模型如圖2所示，模型邊界條件按照簡支梁受力模式施加。

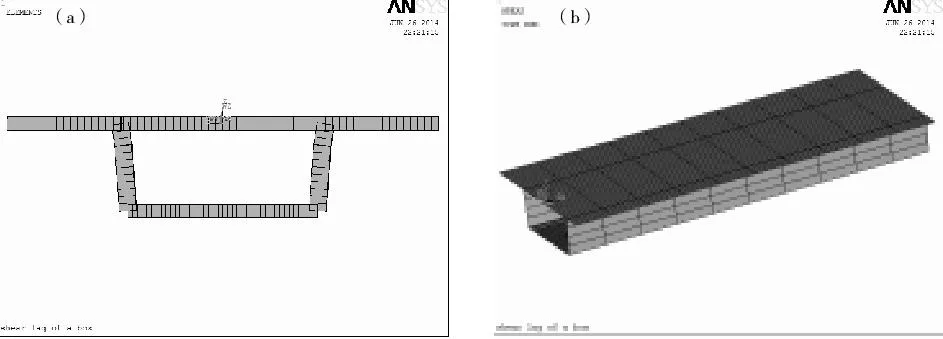
(a)橫截面；(b)空間透視圖2　有限元模型Fig.2 Finite element model

1.3荷載施加

畸變效應是箱梁空間復合受力中的一種變形模式。當箱梁橫截面上作用有偏心距e的荷載ΣP時，如圖3(a)，根據截面荷載等效原則[4]，可分解為3種獨立的變形模式：豎向彎曲，如圖3(d)；剛性扭轉，如圖3(e)；畸變，如圖3(f)。

雙線鐵路箱梁只有雙線列車完全同步行進時符合對稱受力特點，事實上這種完全對稱的情況非常少見。因此上雙線鐵路在運營中絕大多數時候都會存在偏心活載作用，特別是當僅單線通過列車時偏心力矩最大。

根據現有設計規范[11]，客運專線鐵路設計采用ZK活載，沖擊系數取為1.08。對雙線鐵路箱梁，根據規范應該按照特種活載計算畸變效應。僅單線活載作用時由于偏心作用會產生梁體畸變效應，如圖4所示。

由圖3荷載分解方式，依據畸變荷載分解原理[4-5]，可確定出單個特種活載集中力引起的畸變荷載為：

(1)

(2)

(3)

在圖2模型中，通過在研究的最不利位置施加式(1)～(3)計算獲得的畸變荷載，進行求解后得到的縱向應力，即為畸變翹曲應力。

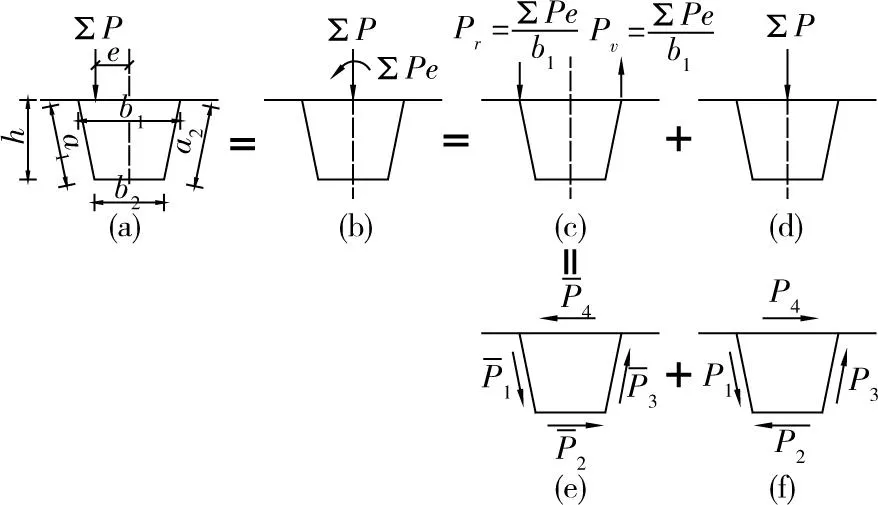
圖3　偏心荷載的分解Fig.3 Decomposition of eccentric load

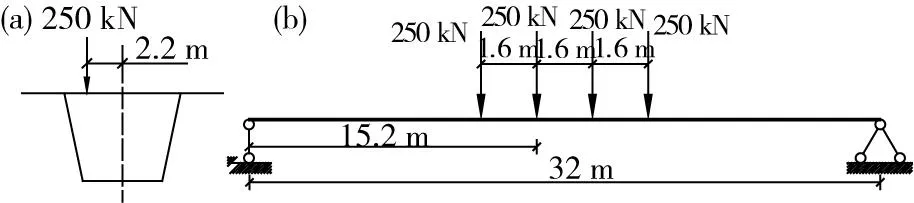
(a)橫向；(b)縱向圖4　加載示意圖Fig.4 Schematic diagram of loading

2鐵路箱梁畸變翹曲應力數值解與理論解對比

2.1跨中截面的畸變效應

對上述的箱梁，計算僅單線活載最不利(按特種活載布置在跨中位置)作用時，單線偏心活載由于畸變產生翹曲正應力。同時，采用傳統畸變效應計算的解析方法[4-5]，計算相應的翹曲縱向正應力，與板殼有限元解進行對比，結果如圖5所示。

從圖5可以看出，基于板殼的有限元解與傳統解析解在數值大小和變化趨勢方面均較為接近，表明有限元方法可以模擬箱梁空間力學特性中的畸變效應。由于傳統解析解是建立在理想的一維歐拉梁理論上的解析方法，應力結果為理想直線規律，這與實際箱梁空間受力特性存在一定偏差。通過板殼有限元方法，可以反映出箱梁空間板系受力特點，其結果更為真實可靠。

注：括號外為板殼有限元解，括號內為理論解析解單位：kPa圖5　跨中截面翹曲應力分布Fig.5 Warping stress distribution on mid-span section

應力結果表明，箱梁在單線活載作用下，跨中截面腹板與底板連接點部位的畸變翹曲應力數值大于截面其余部位，表明對客運專線雙線箱梁，邊腹板和底板相連部位是畸變效應最突出的部位。

2.2鐵路箱梁跨中截面畸變翹曲應力分析

為了比較雙線箱梁翹曲應力的相對大小，引入翹曲比例系數ξ，其表達式為：

(4)

式中：σdw為計算點在偏心活載下產生的畸變翹曲縱向應力；σz為單線活載產生的包括畸變翹曲在內的總的縱向應力。可以看出，翹曲比例系數反映活載畸變效應產生的縱向正應力占總的正應力的百分比。

為了反映箱梁截面上不同部位的畸變程度，將箱梁跨中截面頂板、底板、腹板沿各自板塊均勻分成10等份,分析翹曲比例系數ξ的規律，結果如圖6所示。

從圖6中可以看出，雙線鐵路箱梁在僅單線活載最不利作用時，跨中截面頂板及底板的翹曲比例系數ξ越遠離截面中心越大，且沿板箱梁中線向兩側近似線性增大，頂板翹曲比例系數略大于底板。腹板的翹曲比例系數整體大于頂、底板，這是由于腹板以主要傳遞剪應力為主，因此式(1)中分母較小，故數值偏大。

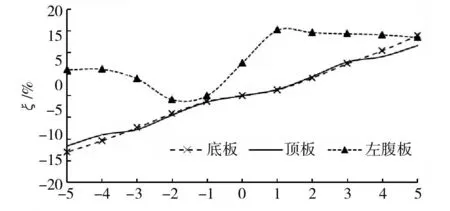
圖6　跨中截面翹曲比例系數ξFig.6 Distortion ratio on mid-span section

數值表明，翹曲比例系數ξ最大的點為：1)頂板翼緣板端部，翹曲比例系數ξ最大達11.6%；2)腹板與底板相交處，翹曲比例系數ξ最大達達13.9%。3)腹板上靠近截面形心位置處，翹曲比例系數ξ最大達15.1%。

3設計參數對畸變翹曲比例系數ξ的影響

3.1高跨比對翹曲比例系數ξ的影響

高跨比(h/l)是箱梁重要的設計參數之一。以圖1所示客專雙線箱梁為例，進一步研究高跨比變化對畸變效應的影響。結合前述分析，選擇箱梁截面上畸變效應突出的3個點，作為應力分析控制點：

1)1號點，位于左腹板與底板的交界部位;

2)2號點，位于左腹板與頂板的交界部位;

3)3號點，位于頂板翼緣板懸臂端部。

計算中，以32 m標準跨度為參照，通過改變橋梁跨度l，實現高跨比的改變。不同高跨比情況下，跨中截面和l/4截面的三個控制點部位的翹曲比例系數ξ的分布規律如圖7所示。

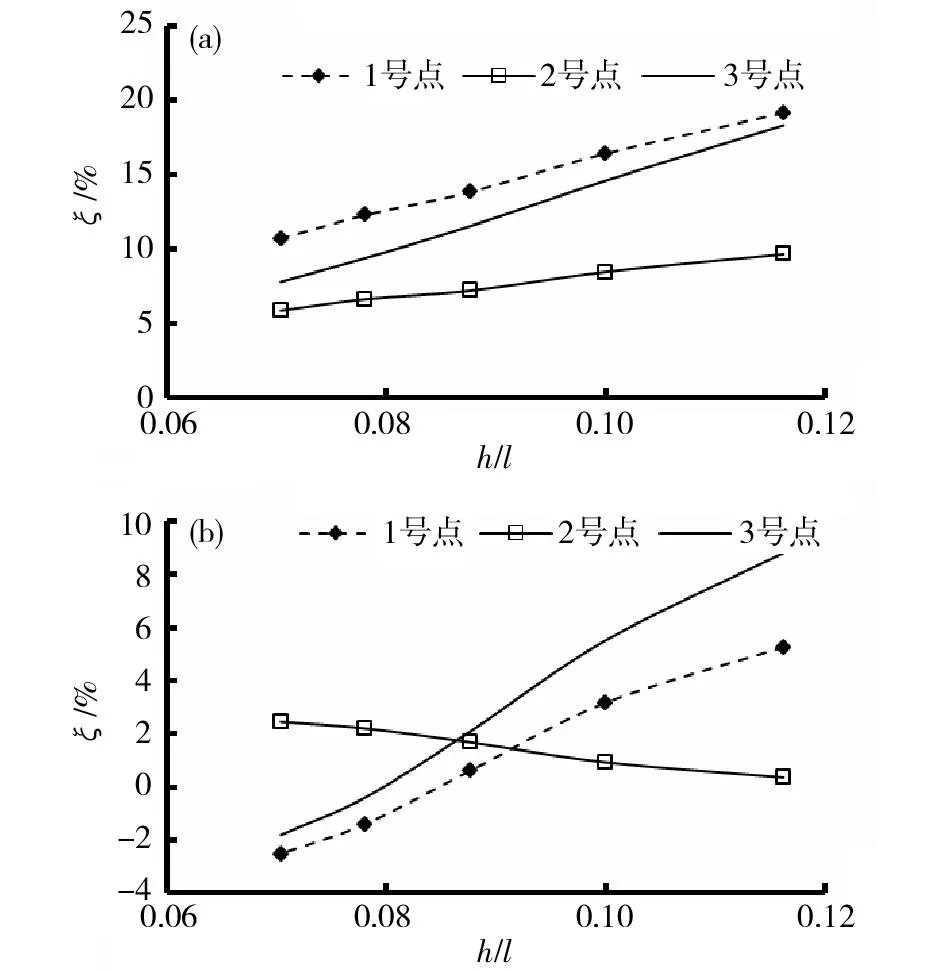
(a)跨中截面；(b)l/4截面圖7　高跨比對翹曲比例系數ξ的影響Fig.7 Effect of high span ratio on distortion ratio

從圖7(a)中可以看出，跨中截面3個點的翹曲比例系數ξ隨高跨比的增大近似呈線性增大，反映出箱梁跨度越小，畸變效應越突出。由曲線斜率可以看出，3號點部位、即頂板懸臂端部的畸變效應受高跨比影響最為突出，其次為1號點，2號點的畸變隨高跨比變化較小。

從圖7(b)中可以看出，l/4截面的畸變效應總體上小于跨中截面。l/4截面1號點和3號點隨高跨比增大時翹曲比例系數ξ增大，而2號點減小。與跨中截面類似，3號點部位、即頂板懸臂端部的畸變效應受高跨比影響最為突出。

綜合而言，對應于32 m標準跨度時的高跨比0.09，跨中截面的翹曲比例系數ξ總體上小于15%，而l/4截面的翹曲比例系數ξ接近于0，說明既有標準設計的高跨比設置對畸變效應不敏感，是非常合理的設計參數取值。

3.2截面參數對畸變翹曲比例系數ξ的影響

截面寬高比(b/h)、截面壁厚δ也是對截面畸變效應有較大影響的參數，在圖1標準設計的基礎上，進一步研究b/h和δ變化對翹曲比例系數的影響。研究中，選擇畸變效應最大的1號點為研究對象。計算跨徑分別取24，32和40 m；箱壁厚度δ主要考慮頂、底板平均厚度，分別取20，30和40 cm；其中寬高比通過保持底板b不變而高度h改變實現。不同跨度下，b/h和δ變化對跨中截面1號點的翹曲比例系數影響趨勢如圖8所示。

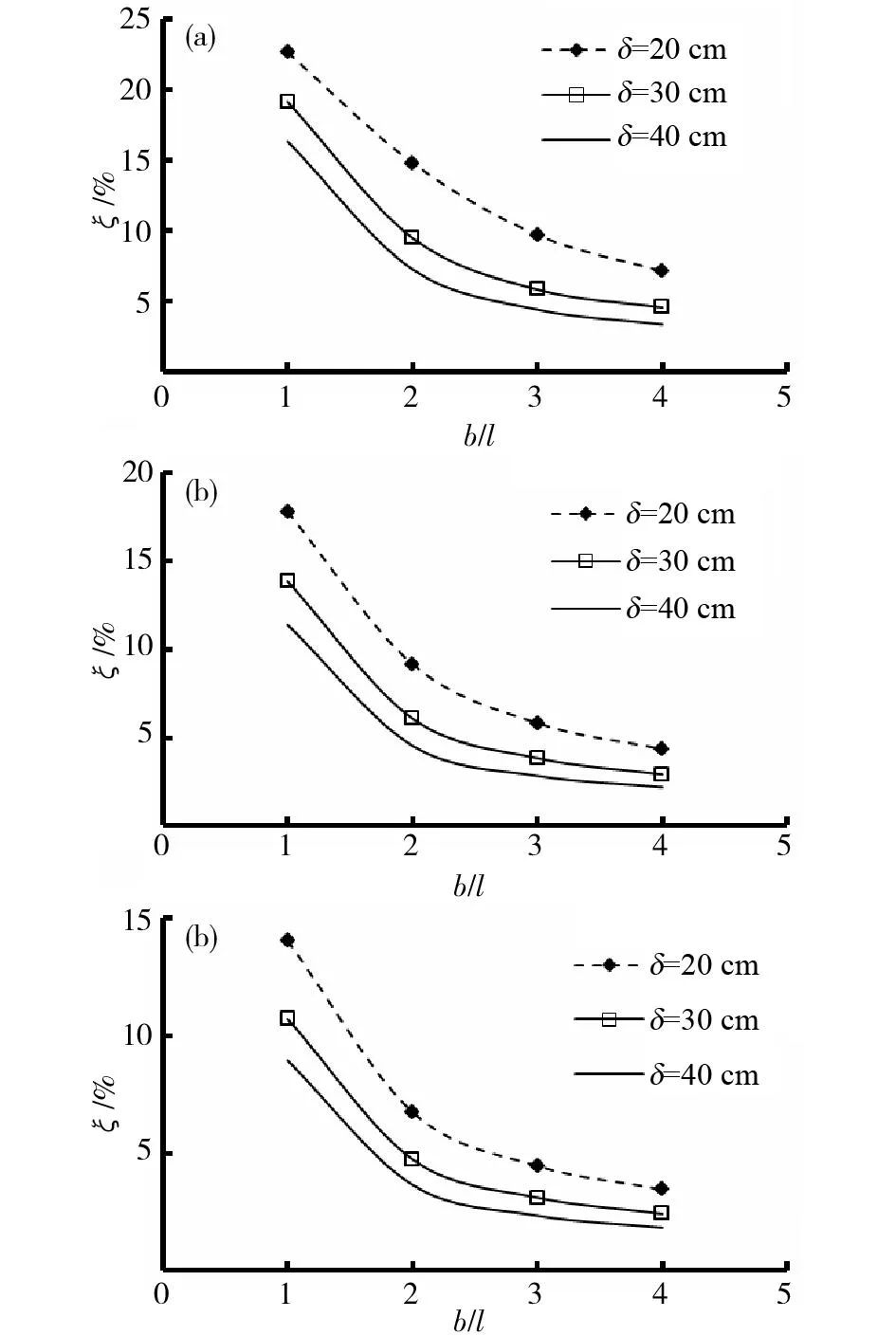
(a)計算跨徑24 m；(b) 計算跨徑32 m；(c)計算跨徑40 m圖8　截面參數對翹曲比例系數ξ的影響Fig.8 Effect of sectional parameters on distortion ratio

由圖8可以看出，不同跨度下的翹曲比例系數對比表明，跨度越大畸變效應越小，這與3.1節規律一致。在箱梁跨徑一定的情況下，翹曲比例系數ξ隨寬高比增大而減小，說明截面高度越大、畸變效應越突出，截面底板寬度越小、畸變效應越突出。不同壁厚結果表明，壁厚越大翹曲比例系數越小，說明增大壁厚增加可抑制畸變效應。

4結論

1)雙線鐵路箱梁在僅單線活載最不利作用時，腹板與底板的交界部位、腹板與頂板的交界部位和頂板翼緣板懸臂端部為翹曲正應力較大部位，其中腹板與底板交界部位應力最大，設計ZK特種活載下的畸變產生的縱向正應力可達總縱向應力的14%。設計中應充分考慮畸變對橋梁受力的影響。

2)現有時速250 km/h鐵路32 m跨度雙線標準箱梁跨中和l/4截面的畸變效應分析表明，既有設計的截面參數對應的高跨比0.09是最優的高跨比，此時跨中最大翹曲比例系數小于15%，而l/4截面的翹曲比例系數ξ接近于0。

3)箱梁高跨比、寬高比、壁厚等設計參數對畸變效應均有一定影響，總體規律是高跨比越大，畸變效應越小；跨高比越大，畸變效應越小；壁厚越大，畸變效應越小。

參考文獻：

[1] 鄭健. 中國高速鐵路橋梁[M]. 北京: 高等教育出版社, 2008.

ZHENG Jian. High-speed bridge engineering in China[M]. Beijing： Higher Education Press, 2008.

[2] 賈衛華. 武廣高速鐵路雙線整孔簡支箱梁預制技術[J]. 鐵道科學與工程學報, 2010,17(2): 74-78.

JIA Weihua. Prefabricating technology of double line whole-span simply supported box girder in Wuguang high speed railway [J]. Journal of Railway Science and Engineering, 2010,17(2): 74-78.

[3] TB10002.3—2005,鐵路橋涵鋼筋混凝土和預應力混凝土結構設計規范[S].

TB10002.3—2005, Code for design on reinforced and prestressed concrete structure of railway bridge and culvert [S].

[4] 項海帆.高等橋梁結構理論[M]．2版.北京: 人民交通出版社, 2013．

XIANG Haifan．The higher bridge structure theory[M]．2nd edition. Beijing: China Communications Press，2013．

[5] 郭金瓊，房貞政，鄭振. 箱形梁設計理論[M]. 2版.北京:人民交通出版社, 2008.

GUO Jinqiong, FANG Zhenzhen, ZENG Zhen.Design theory of box girder[M]. 2nd edition.Beijing:China Communications Press, 2008.

[6] Jonsson J. Distortional theory of thin-walled beams [J]. Thin-Walled Structures, 1999,33(4): 269-303.

[7] 張士鐸, 劉吉柱. 單室薄壁梯形箱梁的畸變應力[J]. 北京工業大學學報, 1987,13(1): 79-92.

ZHANG Shiduo, LIU Jizhu. Distortion stress in a trapezoidal box girder with single-cell [J]. Journal of Beijing Uuniversity of Technology, 1987, 13(1): 79-92.

[8] 徐勛, 強士中. 薄壁箱梁畸變分析理論的研究[J]. 工程力學, 2013, 30(11): 192-201.

XU Xun, QIANG Shizhong.Researchon distortion ananlysis theory of thin-walled box girder[J]. Engineering Mechanics, 2013, 30(11): 192-201.

[9] Ghani Razaqpur A, Li Hangang. Thin-walled multicell box-girder finite element[J].Journal of Structural Engineering,1991, 117(10):2953-2971.

[10] 張莉. 橫隔板及幾何特征對鋼箱梁畸變效應的影響[J]. 鐵道工程學報，2013, 29(8)：68-73.

ZHANG Li. Influences of diaphragm plate and geometric characteristics on distortion effect of steel box girder[J].Journal of Railway Engineering Society, 2013, 29(8):68-73.

[11] TB 10020—2009, 高速鐵路設計規范(試行)[S].

TB 10020—2009, Code for design of high speed railway[S].

Distortion effect of double track railway box girders with speed of 250 km/h

LIN Pengzhen,SUN Lixiang，JI Wei , YANG Zijiang

(Key Laboratory of Road Bridge and Underground Engineering Gansu Province, Lanzhou Jiaotong University, Lanzhou 730070, China)

Abstract:In order to calculate the distortion effect of double track railway box girders at the speed of 250 km/h, a numerical model is established based on shell finite element method. Using finite element method and the traditional analytical method, distortion stress is calculated and analyzed under only single track live load. By defining the parameters of warping ratio, the rules of warping stress influenced by the design parameters of high span ratio, width span ratio and wall thickness are analyzed. Comparing with the traditional analytical solution, the finite element method is more suitable for the analysis in the box girder distortion effect. Under eccentric live load of single track, the value of warping ratio on flange edge of top plate is 11.6%, while it is 13.9% near the intersection of the web and the bottom plate which is the maximum in mid-span section. Analyzing the warping ratio on sections of mid-span and l/4, it is shown that the beam design parameters of existing box is reasonable. The maximum warping ratio on mid-span section is less than 15%, while nearly 0 on l/4 section. The design parameters of high span ratio, width span ratio and wall thickness can influence the sectional distortion of box girder. It is found that the distortion effect decreases with the increase of the high span ratio, width span ratio and wall thickness.

Key words：railway box girder；distortion；warping stress；numerical analysis

中圖分類號：U441+.5

文獻標志碼：A

文章編號：1672-7029(2016)04-0595-05

通訊作者：藺鵬臻(1977-)，男，甘肅甘谷人，甘肅省“飛天學者”特聘教授，博士，從事橋梁結構設計理論的研究；E-mail：pzhlin@mail.lzjtu.cn

基金項目：國家自然科學基金資助項目(51368031);甘肅省基礎研究創新群體項目資助(1506RJIA029)

收稿日期：2015-09-08