基于ε-Voronoi圖的矢量數據自適應簡化方法

張 振 鑫,鄧 浩,寇 一 丹,張 維,劉 嬪

(1.北京師范大學地理學與遙感科學學院遙感科學國家重點實驗室，北京 100875；2.中南大學地球科學與信息物理學院,湖南 長沙 410083；3.中南大學信息科學與工程學院,湖南 長沙 410083)

基于ε-Voronoi圖的矢量數據自適應簡化方法

張 振 鑫1,鄧 浩2,寇 一 丹1,張 維2,劉 嬪3

(1.北京師范大學地理學與遙感科學學院遙感科學國家重點實驗室，北京 100875；2.中南大學地球科學與信息物理學院,湖南 長沙 410083；3.中南大學信息科學與工程學院,湖南 長沙 410083)

針對矢量數據簡化的問題，提出一種基于幀緩存和四叉樹索引的自適應簡化方法，即采用四叉樹索引對矢量數據進行區域劃分，通過評價各個區域地物實體分布密度的指標，判斷各個區域內的矢量數據密度、圖幅寬度，得到各區域ε-Voronoi圖中的ε值，再借助幀緩存技術，自適應地簡化各個區域內的矢量數據。實驗表明，該方法一定程度上提高了簡化質量，為矢量數據可視化應用提供一定的基礎。

四叉樹；幀緩存；自適應；簡化

0 引言

隨著硬件平臺及相關技術的發展，人們獲取空間數據的能力急劇增長，甚至超出計算機存儲能力的增長速度。這些數據包含大量的空間矢量數據，對矢量數據的可視化是矢量數據應用的一個重要方面[1]，矢量數據簡化又是空間數據可視化研究的重要內容。

矢量數據簡化研究源于Douglas與Peuker提出的Douglas-Peuker折線簡化法[2],該方法效率較高，且可保持線要素的重要幾何特征，但在簡化過程中會導致拓撲關系發生改變，造成簡化后的線要素可能出現自相交等拓撲關系不一致錯誤[3]。Guibas等[4]證明:在避免自相交的情況下，保留盡可能少的點是一個NP-hard問題。Estkowski[5]等在Douglas-Peuker算法的基礎上，采用“繞遠之路(detour)”的方式避免簡化后的自相交，該算法的時間復雜度最高為O(n3)，且運行速度較慢；Yang 等[6]采用Visvalingam-Whyattt算法，并結合約束條件的限制，避免了簡化后的自相交，時間復雜度為O(nlogn)，但多分辨率空間編碼帶有一定的冗余，影響了簡化效率。文獻[7，8]采用矢量數據頂點聚類的方式，即選出每個聚類中的一個點來代替每個聚類中的點，但該方法在避免簡化后線段間的自相交方面仍顯不足。Mustafa 等[9]提出了一種基于ε-Voronoi圖的簡化方法，即通過模板深度緩存，將ε-Voronoi區域渲染到模板緩存中，再通過模板測試，剔除ε-Voronoi區域外的點，保證每個要素簡化結果都位于ε-Voronoi區域中，一定程度上可避免要素間的相交，但不能避免要素內部的自相交，因為每個矢量實體的ε值固定，該簡化方法在靈活性和自適應性方面略有欠缺，且沒有考慮待簡化區域地物分布密集程度對簡化的影響。Yang等[10]通過引進單調鏈[11]，提出了一種基于幀緩存和ε-Voronoi圖的簡化方法，通過剔除模板外不合規線段進行簡化，一定程度上避免了簡化后要素間的相交和每個要素內部的自相交，但該方法存在以下問題：1)ε值靈活性不夠，導致不同分布密度的矢量數據都在相同的ε值下簡化，進而導致生成ε-Voronoi圖較困難，甚至一些矢量地物的ε-Voronoi圖將距離較近的其他矢量實體的ε-Voronoi圖完全覆蓋，導致簡化結果出現拓撲錯誤；2)借助幀緩存剔除違規線段，當待簡化的矢量數據數量較多時，一些矢量數據可能映射到較少甚至幾個像素中，會導致剔除違規線段時出現異常，簡化結果出現拓撲錯誤。由于地物空間分布多樣性及復雜性，亟須一種根據矢量地物分布疏密程度的自適應簡化方法以提高簡化質量。

本文提出一種基于幀緩存和四叉樹的矢量數據自適應簡化方法，通過對矢量數據建立四叉樹索引，對區域進行劃分，在評價每個子區域矢量數據密集程度的基礎上，確定每個葉子節點區域的ε值，使每個葉子節點區域簡化與該區域的矢量實體分布的密集程度相適應，提高簡化質量。

1 矢量數據區域劃分

通過建立矢量數據的四叉樹索引進行區域劃分。首先，設定四叉樹葉子節點中矢量地物數目閾值，而后以每個矢量地物(polyline或polygon)的最小外包矩形(MBR)中心點為四叉樹劃分的基本點，進行四叉樹區域劃分。為更好地評價各個子區域的分布密度，需要保證每個葉子節點區域的范圍一致，因此，本研究采用完全四叉樹的方式進行區域劃分。設每個葉子節點中實體數目的閾值為m， 矢量數據完全四叉樹構建的步驟如下：1)遍歷矢量數據，統計位于各個子節點矢量數據MBR中心點的數量γ。2)如果位于所有子節點矢量數據的數目γ都小于m，則完全四叉樹構建完畢；反之，四叉樹深度增加，各個子節點分裂成4個新的子節點，重復執行步驟1)，直到所有子節點中矢量實體的數目都小于m，四叉樹構建完畢，將對應的矢量實體劃歸到各個四叉樹葉子節點中。圖1是閾值為2的完全四叉樹的區域劃分結果。

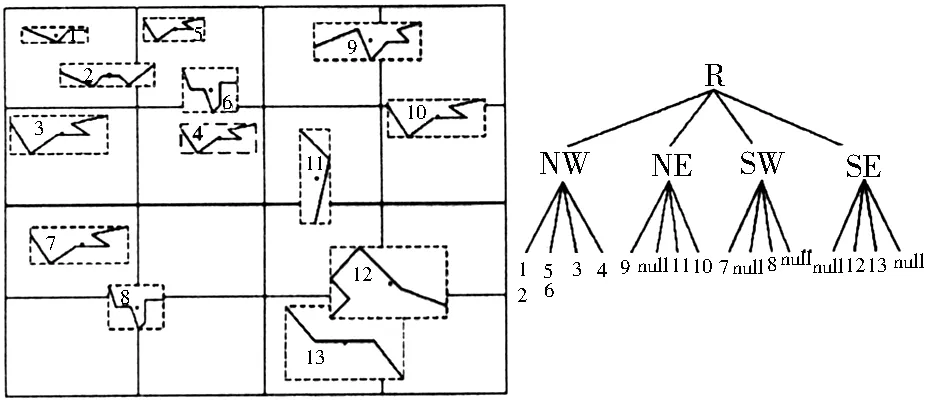
圖1 矢量數據的四叉樹劃分

Fig.1 Dividing the vector data by Quadtree

2 基于幀緩存簡化

2.1 矢量實體的εi-Voronoi圖定義

εi-Voronoi圖即具有距離約束條件εi的Voronoi圖，每個εi-Voronoi圖內的點到其矢量數據對象的最小距離不大于εi值。設矢量數據集合G是由n個矢量實體組成，即g1,g2,…,gn∈G，定義gi的εi-Voronoi圖(簡稱εi-V(gi))為所有到gi的距離不大于εi的點的集合，即εi-V(gi)={p|dist(p,gi)≤dist(p,gj),dist(p,gi)≤εi,i≠j,j=1,2,…,n}，則G的εi-Voronoi圖的集合為εi-V(G)={ε1-V(g1),ε2-V(g2),…,εn-V(gn)}，如圖2所示，ε1、ε2、ε3形成3條矢量地物實體的εi-Voronoi圖的集合。

2.2 自適應參數εi值的計算

本文的自適應簡化方法是通過四叉樹葉子區域的道路分布密度、葉子節點區域寬度和參數自適應地確定εi-Voronoi圖中εi值實現的，過程如下:

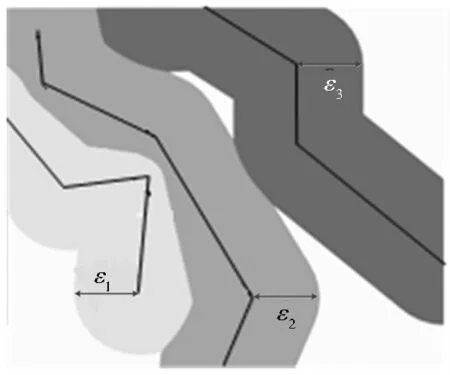
圖2 εi-Voronoi圖示意

Fig.2εi-Voronoi diagram

首先，設計衡量各個葉子節點區域矢量數據密度(σi)的方法：

(1)

其中:ki代表第i個葉子節點包含的所有矢量數據映射到幀緩存后各個矢量數據對應像素的數目總和；Si代表第i個葉子節點區域映射到幀緩存后該區域所覆蓋的像素數目；kimax是第i個葉子節點進一步四分后(圖3虛線分割后的區域)各個子區域像素數目的最大值；kimin是第i個葉子節點四分后，子區域中地物投影到幀緩存后像素數目的最小值。

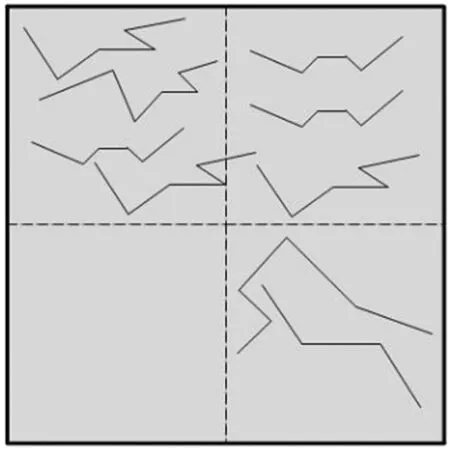
圖3 葉子節點四分示意

Fig.3 Leaf nodes of the quad-tree

接著，取各個葉子節點區域密度的最大值σm,再將每個葉子節點區域的密度與σm的比值作為每個葉子節點區域的相對密度δi，即:

(2)

這樣，每個葉子節點中的各矢量元素的εi值為:

εi=δi×di×α

(3)

α表示提前設定的參數，di是第i個葉子節點的圖幅寬度。δi越大，表示地物越密集。圖4是不同葉子節點下的矢量數據分布密度示意圖。

2.3 矢量數據的簡化

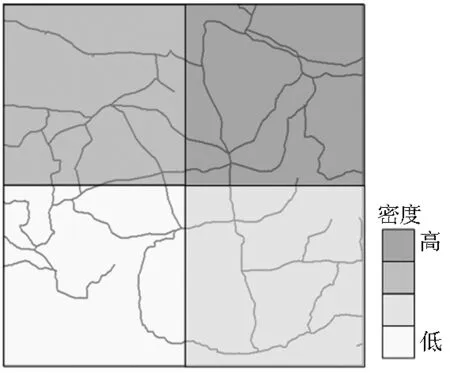
圖4 葉子節點矢量地物分布密度示意

Fig.4 The density of vector data in each leaf node

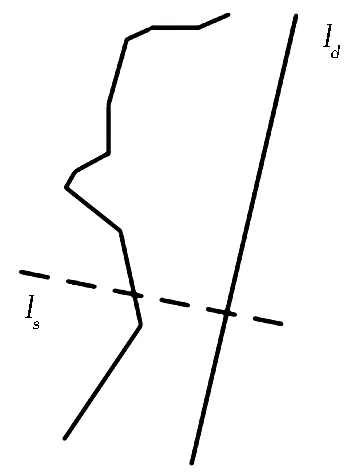
圖5 單調鏈示意

Fig.5 Monotone chain diagram

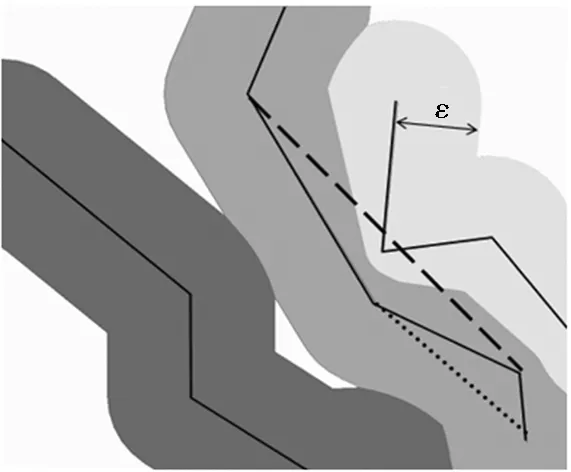
圖6 εi-Voronoi圖區域、合規線段(短虛線)和違規線段(長虛線)

Fig.6εi-Voronoi diagram,compliance line and irregular line

圖7 線要素的簡化過程

Fig.7 The procedure of line object simplification

3 實驗驗證與分析

3.1 數據集

表1是本研究所采用的數據集,該數據集的空間分布存在一定差異性，要素之間存在著較為復雜的拓撲幾何關系。

表1 數據集

Table 1 Datesets

數據集序號名稱類型要素個數節點數目1中國縣級區劃圖polyline113336097322北京市交通圖polyline155155955366

3.2 與其他方法對比

采用本文方法得到簡化結果,并與文獻[10]的方法進行對比(圖8、圖9)。本文方法的四叉樹閾值設為100，α初始值設為0.005。本方法(圖8b)與采用文獻[10]的方法(圖8c)得到的簡化結果相比，更好地保持了簡化前的拓撲關系，在文獻[10]的方法下，一些較復雜區域的簡化出現簡化后相交的拓撲錯誤問題，本文方法可很好地保持原始數據的拓撲關系。對數據集2(圖9a)，在立交橋區域，與文獻[10]的方法(圖9c)得到的結果相比，本文方法(圖9b)能夠更好地保持立交橋的原始形態特征及道路間的連通關系，得到更高質量的簡化結果。

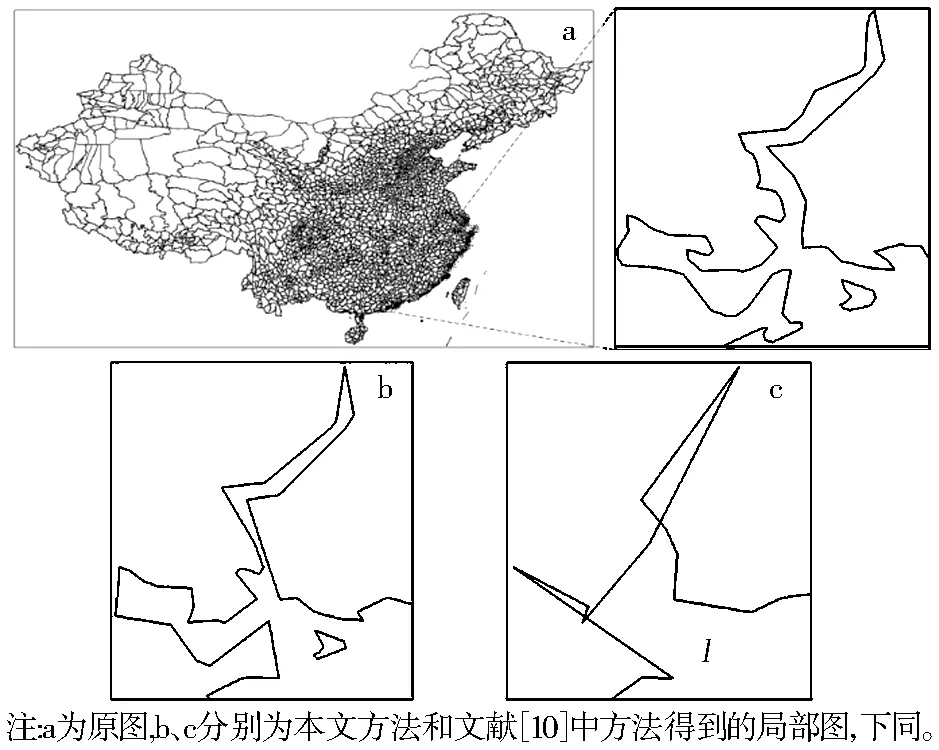
圖8 數據集1的簡化結果及對比

Fig.8 The result and comparison of simplification about dataset 1

上述是從直觀、可視的角度進行的對比，為了全面評價兩種方法的簡化結果，首先，對簡化后的數據出現拓撲異常的情況進行說明，即簡化后各個簡化實體內部或實體間與簡化前不一致，稱之為異常。接著，對簡化后矢量數據發生拓撲異常的實體數目和簡化后的實體節點數目總和進行統計(表2)。從表2可以看出，本文方法分別對數據集1和數據集2簡化后出現的拓撲異常實體數目為33和920，文獻[10]的方法對數據集1和數據集2簡化后出現的拓撲異常實體數目為420和3 370，本文方法在保持實體簡化拓撲正確性方面有明顯優勢；在簡化后剩余節點數方面，本文方法對數據集1和數據集2簡化后的實體節點數目總和分別為423 500和507 873，而文獻[10]的方法對數據集1和數據集2簡化后的實體節點數目總和分別為366 321和429 564，再結合圖8b和圖9b可以看出，本文方法簡化后保留更多節點以避免發生拓撲異常。

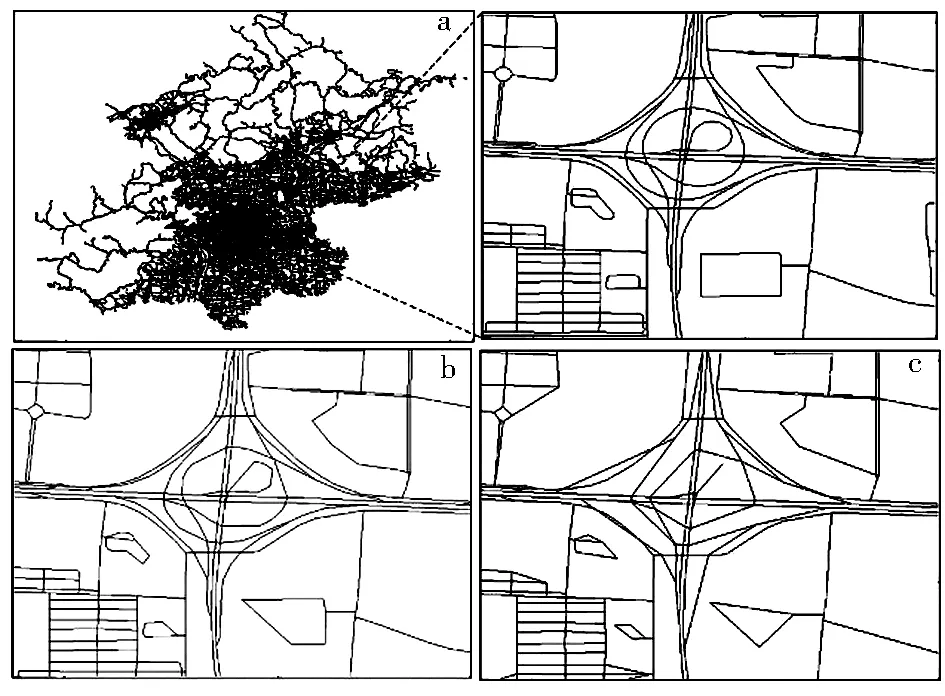
圖9 數據集2的簡化結果及對比

Fig.9 The result and comparison of simplification for dataset 2

表2 兩種方法簡化結果的統計對比

Table 2 Statistical comparison of simplification results using two methods

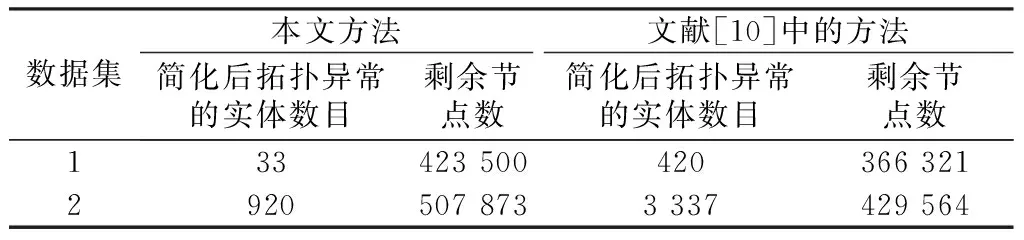
數據集本文方法文獻[10]中的方法簡化后拓撲異常的實體數目剩余節點數簡化后拓撲異常的實體數目剩余節點數13342350042036632129205078733337429564

3.3 算法效率

本算法測試的硬件環境為：Intel Core i7-4770，cpu ：3.4 GHz和8 G的RAM。軟件環境：操作系統為32位的Windows 7，集成開發環境是Visual C2010。對本方法的效率進行了測試，對數據集1的簡化時間為143 s，數據集2的簡化時間為119 s，以上測試是在單機串行的環境下進行的。

3.4 參數的敏感性測試

算法測試采用兩組參數，第一組：四叉樹劃分閾值分別為50、100、150、200，α為0.005；第二組：四叉樹劃分閾值為100，α分別為0.003、0.005、0.007、0.009。本次測試以簡化后矢量數據拓撲的正確率為測試標準，這里，矢量數據出現簡化拓撲錯誤有以下幾種情況：簡化前數據間相交，簡化后不相交；簡化前數據間不相交，簡化后相交；簡化前數據內部不相交，簡化后相交；簡化前數據內部相交，簡化后不相交。從圖10可以看出，當四叉樹索引閾值為100時，得到較高的簡化正確率，說明這兩套數據在四叉樹索引閾值是100時，簡化效果較好。從圖11可得，隨著α值的增大，簡化后具有正確拓撲關系的矢量數據逐漸減少，這是由于隨著α值增加，εi值隨之增加，導致較少的線段被判斷為違規線段，簡化程度較大，出現簡化后拓撲錯誤的矢量數據數目也隨之增加。

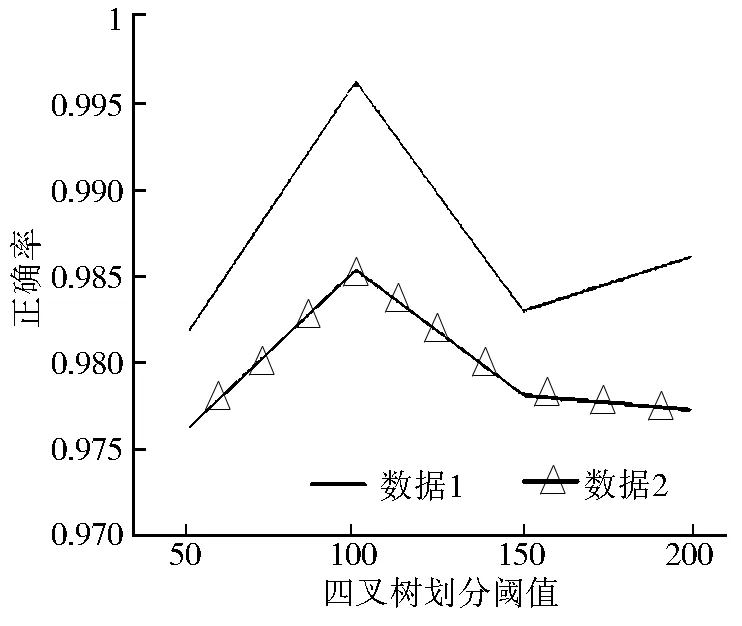
圖10 不同四叉樹劃分閾值下的正確率測試

Fig.10 Accuracy rate test in different thresholds of Quadtree construction

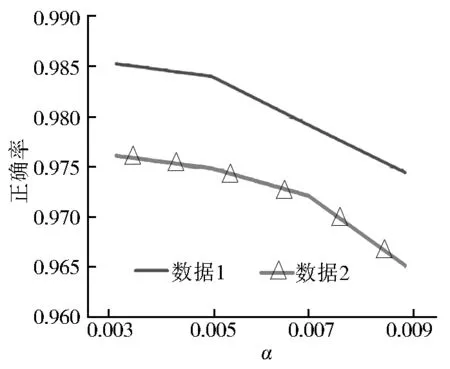
圖11 不同α值下的正確率測試

Fig.11 Accuracy rate test in differentαvalue

4 結論

本研究基于矢量數據的完全四叉樹索引構建子區域，提出了葉子節點子區域的數據分布密度評價指標，各個葉子節點區域根據各自的密度進行自適應簡化，并通過與前人的方法對比可以看出，在簡化質量上，本文方法有一定的提高，尤其是對空間分布差異較大的數據簡化效果更好。后續工作將考慮采用并行方式，通過對并行簡化框架的設計，將本方法進行并行化實驗，進一步提高簡化效率。

[1] GOODCHILD M F.Geographical information science[J].International Journal of Geographical Information Systems,1992,6(1):31-45.

[2] DOUGLAS D H,PEUCKER T K.Algorithms for the reduction of the number of points required to rep resent a digitized line or its caricature[J].The Canadian Cartographer,1973,10(2):112-122.

[3] ZHAN H S,LI G X.Progressive transmission of vector map data based on polygonal chain simp lification[J].Lecture Notes in Computer Science,2006,4282:908-917.

[4] GUIBAS L J,HERSHBERGER J,MITCHELL J,et a1．Approximating polygons and subdivisions with minimum link paths[J]．Lecture Notes in Computer Science,1993(3):383-415.

[5] ESTKOWSKI N,MITCHELL J S B.Simplifying a polygonal subdivision while keeping it simple[A].Proceedings of the 17th ACM Symposium on Computational Geometry[C].2001.40-49.

[6] YANG B,PURVES R,WEIBEL R.Efficient transmission of vector data over the Internet[J].International Journal of Geographical Information Science,2007,21(2):215-237.

[7] RAPOSO P.Scale-specific automated line simplification by vertex clustering on a hexagonal tessellation[J].Cartography and Geographic Information Science,2013,40(5):427-443.

[8] 李進,馬勁松,沈婕,等.一種基于頂點聚類的線要素簡化算法改進[J].測繪科學技術學報,2013,30(5):525-529.

[9] MUSTAFA N,KRISHNAN S,VARADHAN G,et al.Dynamic simplification and visualization of large maps[J].International Journal of Geographical Information Science,2006,20(3):273-302.

[10] YANG L,ZHANG L,MA J,et al.Efficient simplification of large vector maps rendered onto 3D landscapes[J].Computer Graphics and Applications,IEEE,2011,31(2):14-23.

[11] CHANDRU V,RAJAN V T,SWAMINATHAN R.Monotone pieces of chains[J].ORSA Journal on Computing,1992,4(4):439-446.

[12] HOFF III K E,KEYSER J,LIN M,et al.Fast computation of generalized Voronoi diagrams using graphics hardware[A].Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques[C].ACM Press/Addison-Wesley Publishing Co.,1999.277-286.

An Adaptive Simplification Method on Vector Data Based onε-Voronoi

ZHANG Zhen-xin1,DENG Hao2,KOU Yi-dan1,ZHANG Wei2,LIU Bin3

(1.State Key Laboratory of Remote Sensing Science,School of Geography and RS,Beijing Normal University,Beijing 100875;2.School of Geosciences and Info-Physics，Central South University，Changsha 410083;3.School of Information Science and Engineering,Central South University,Changsha 410083,China)

In this paper,an adaptive method that performs simplification of vector data using frame buffer and quad-tree index is presented.Firstly,indicators to evaluate vector data density are proposed,then the tolerance parameter (ε) ofε-Voronoi diagram is gotten by the vector data density and width of each region.In the end,the vector data is adaptively simplified with the technology of frame buffer.The result of experiment indicates that our method improves the quality of simplification quality,and provides some bases for visualization of vector data.

quad-tree;frame buffer;adaptive;simplification

2015-03-20；

2015-10-19

湖南省博士后科研資助專項計劃(2014RS4028);國家自然科學基金項目(41401532)

張振鑫(1986-),男,博士研究生,從事空間信息可視化算法研究。E-mail:zhenxin066@163.com

10.3969/j.issn.1672-0504.2016.01.006

P283；P208

A

1672-0504(2016)01-0029-05