廣義Fitzhugh-Nagumo方程的無(wú)窮序列新解*

伊麗娜包俊東 套格圖桑

（內(nèi)蒙古師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院，呼和浩特 010022）

廣義Fitzhugh-Nagumo方程的無(wú)窮序列新解*

伊麗娜?包俊東 套格圖桑

（內(nèi)蒙古師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院，呼和浩特 010022）

利用輔助方程的幾種結(jié)論，構(gòu)造了廣義Fitzhugh-Nagumo方程的多種無(wú)窮序列新解.步驟一，利用函數(shù)變換與首次積分，給出了輔助方程的新解、B?cklund變換和解的非線性疊加公式.步驟二，通過函數(shù)變換，將廣義Fitzhugh-Nagumo方程的求解問題轉(zhuǎn)化為非線性常微分方程的求解問題.步驟三，利用符號(hào)計(jì)算系統(tǒng)Mathematica與輔助方程的幾種結(jié)論，構(gòu)造了廣義Fitzhugh-Nagumo方程的多種無(wú)窮序列新解.

廣義Fitzhugh-Nagumo方程， 輔助方程， 首次積分， 無(wú)窮序列新解

引言

在孤立子理論中給出試探函數(shù)法、輔助方程法、同倫映射法和B?cklund變換法等方法，構(gòu)造了具任意次非線性項(xiàng)的非線性發(fā)展方程的新精確解［1-7］.比如：文獻(xiàn)［1］用試探函數(shù)法，構(gòu)造了廣義mKdV方程（1）的新解.文獻(xiàn)［2］用同倫映射法，構(gòu)造了任意次非線性項(xiàng)的非線性發(fā)展方程（2）的新精確解

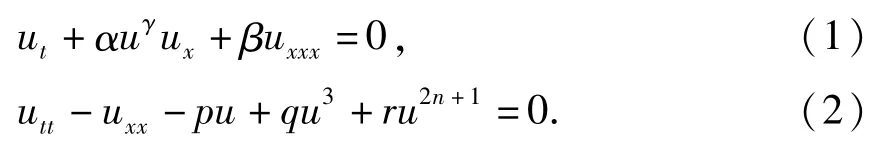
這里α，β，γ是任意非零常數(shù)，p，q，r非負(fù)常數(shù)，n是非零任意常數(shù).

文獻(xiàn)［3-6］用輔助方程法與B?cklund變換法，構(gòu)造了廣義BBM方程和廣義Zakharov-Kuzentsov方程的新精確解

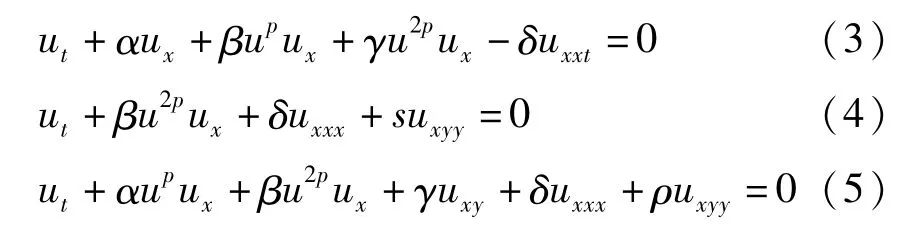
這里α，β，γ，s，δ，ρ是常數(shù)，p是非零常數(shù).

文獻(xiàn)［7］用試探函數(shù)法，構(gòu)造了廣義Fitzhugh-Nagumo方程（6）的指數(shù)函數(shù)型新解這里v，k和p是任意非零常數(shù).

本文用一種輔助方程的幾種結(jié)論，構(gòu)造了廣義Fitzhugh-Nagumo方程的多種無(wú)窮序列新解.步驟一，利用函數(shù)變換與首次積分，給出了輔助方程的新解、B?cklund變換和解的非線性疊加公式.步驟二，通過函數(shù)變換，將廣義Fitzhugh-Nagumo方程的求……