基于擬可積Hamilton系統的鐵路橋梁動力可靠度計算研究

赫中營， 王根會， 葉愛君， 夏修身

（1.河南大學 土木建筑學院，河南 開封 475004；2.蘭州交通大學 土木工程學院，甘肅 蘭州 730070；3.同濟大學 土木工程防災國家重點實驗室，上海 200092）

鐵路橋梁在服役期間，將不可避免的受到諸如地震、風和車輛等動力荷載的作用，動力破壞是其最主要的失效模式之一［1］。由于鐵路橋梁在鐵路運輸網中具有特殊地位，其動力破壞將造成交通運輸中斷，甚至車毀人亡。自1997年以來，我國鐵路運輸大幅度提速增載，使一些既有鐵路橋梁出現振幅和頻率超限問題，橋梁的動力工作性能面臨著巨大的挑戰，迫切需要對鐵路橋梁動力可靠性的分析計算［2］。因此，研究鐵路橋梁結構的動力可靠性將具有十分重要的理論價值和經濟、社會效益。

結構動力可靠性理論是用結構動力學和概率論相結合的方法研究結構在動力隨機荷載作用下的可靠性及相應的設計方法。經過七十余年的發展，國內外結構動力可靠性理論取得了重要成果，并逐步得到完善，其分析方法主要分為以下三類［3］：（1）基于隨機振動理論解析解的動力可靠度計算方法；（2）基于Montecarlo法的動力可靠度計算方法；（3）將動力可靠度問題轉化為系統可靠度問題的計算方法。另外，近年來同濟大學李杰和陳建兵［4－5］基于概率密度演化理論，建立了結構隨機響應分析和動力可靠度分析的廣義概率密度演化方程，可求解線性、非線性及隨機結構的隨機結構反應及動力可靠度，在結構的動力可靠度分析中也得到了一定應用。

由于動力可靠性分析計算的復雜性，對于第一類方法，即使對簡單的首超失效問題，只有Rice S O［6－7］于1945年提出精確解，那也是針對一定前提下的簡單情況。我國工程院院士朱位秋先生等［8－11］提出的隨機動力學與控制的哈密頓理論體系（Hamiltonian system），為研究多自由度體系哈密頓系統的首超問題、估計首超概率及平均首超時間提供了新的思路和解決方法。本文基于哈密頓理論體系中的擬可積Hamilton系統［12－15］，推導出了鐵路橋梁的等價擬可積 Hamilton方程，確定了其在列車荷載作用下的條件可靠度函數及其初始條件和邊界條件，并將理論推導公式應用于一座實際橋梁，對其動力可靠度進行分析，驗證了該方法的合理性和適用性。

1 既有鐵路橋梁的等價擬可積Hamilton系統

所謂等價擬可積Hamilton系統，是指狀態參數（廣義動量、廣義速度等）與相應 Hamilton函數（可積）之間滿足一定關系的物理力學體系。鐵路橋梁的廣義動量、廣義速度與其相應可積Hamilton函數之間滿足的這種物理力學關系（方程）即可稱為其等價擬可積Hamilton系統。

在外荷載激勵下，鐵路橋梁結構體系的振動方程可寫為［16］

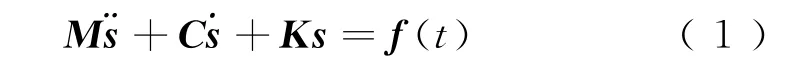
式中：M、C、K分別為結構的質量矩陣、阻尼矩陣和剛度矩陣；s、s和¨s分別為各自由度的位移、速度和加速度列向量，是關于時間t的函數；f（t）為外部激勵荷載。

為便于能量分析，將結構體系的動力學力向量分為保守的和非保守的分量，則式（1）可改寫為

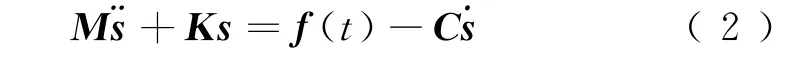
式（2）等式左邊為結構慣性力和結構抗力組成的保守力向量，等式右端為外作用力和阻尼力組成的非保守力向量。

對于空間結構，基于有限元法的能量表達式中未知參數個數為結點個數的6倍，這給計算帶來很大的困難［17］。因此，可考慮利用振型疊加方法表示鐵路混凝土橋梁的振動位移，則其能量表達式將得到極大簡化。

對于橋梁結構動力方程的解s，可通過結構的振型表示為

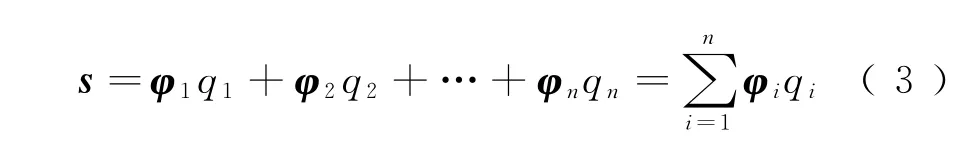
式中：φi（i＝1，…，n）為結構振型，可通過特征方程求得；qi（i＝1，…，n）為振型空間中的坐標值，稱為廣義坐標或結構的正則坐標，表示第i振型（φi）的貢獻。

如果假定阻尼矩陣也適用正交條件，將式（3）代入到式（2），并前乘第i個振型向量的轉置φTi，可得

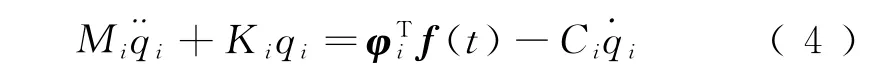
式中：i＝1，…，n；Mi＝分別為結構的廣義質量、廣義阻尼和廣義剛度。

對于線性n自由度離散結構體系，φi為n維列向量，其動能和勢能可分別表示為

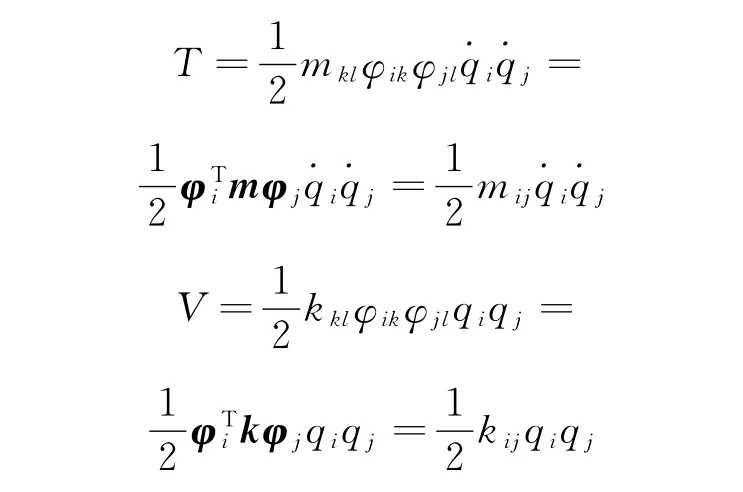
如果體系的各振型對應的頻率都不相等，則任意兩個不同的振型，質量和剛度適用正交條件，式（5）簡化為

對于連續結構體系，i可表示為結構軸向坐標的函數，質量和剛度也都是結構軸向坐標的函數，線性體系的動能和勢能可表示為

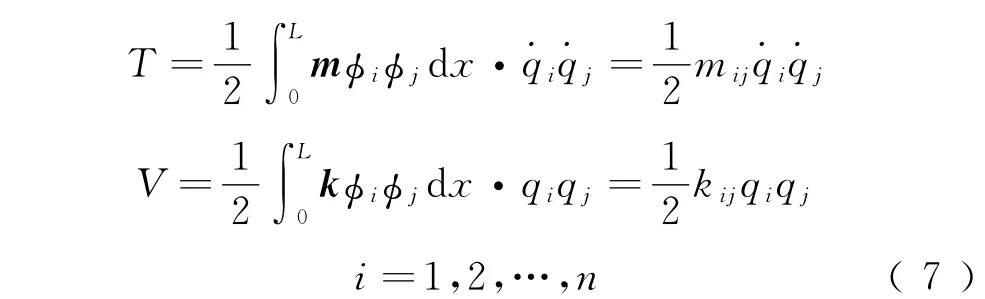
如果體系的各振型對應的頻率都不相等，式（7）簡化為

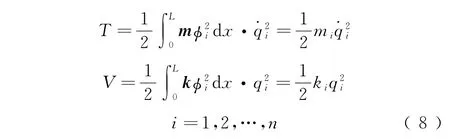
該橋梁結構體系對應的Lagrange函數為

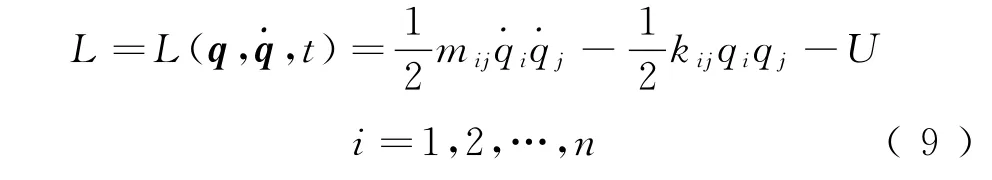
式中：U＝為非保守力所做的功；cij為阻尼系數。qi與qi分別為廣義位移（坐標）與廣義速度，廣義動量可定義為

式（10）稱為由Lagrange函數L生成的Legendre變換，式（10）為非奇異變換、可逆，則其逆變換也是Legendre變換。據Legendre變換的逆變換定理［18］，式（10）之逆變換的生成函數為

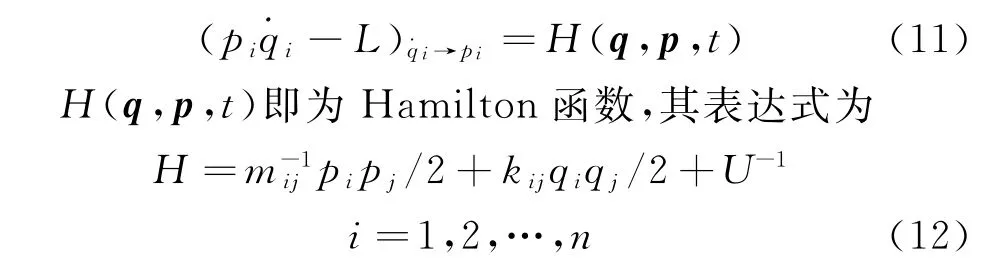
則結構以qi，pi為基本變量的Hamilton方程為

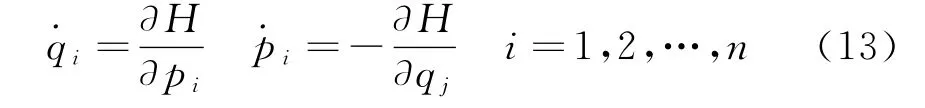
以記隨機激勵的耗散的Hamilton系統的耗散力。以＝fik（q，p）ζk（t）記耗散的Hamilton系統的激勵力，可根據Hamilton原理和Legendre變換導出Gauss白噪聲激勵下n自由度耗散Hamilton系統的運動微分方程形為

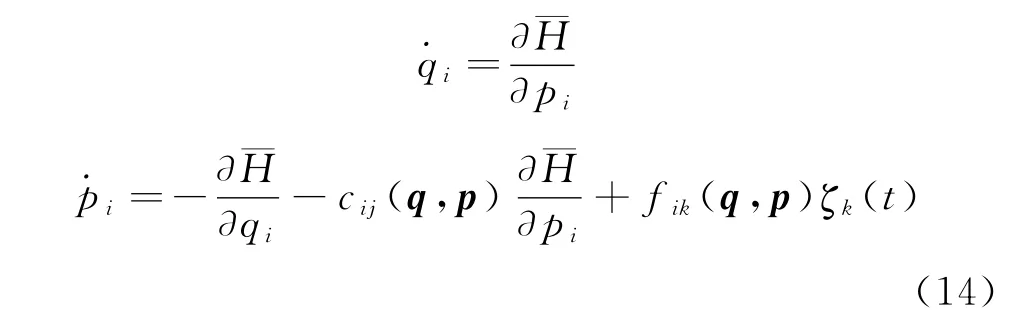
式中：i，j＝1，2，…，n；k＝1，2，…，m，珨H＝珨H（q，p）為未擾Hamilton系統的Hamilton函數；ζk（t）為激勵荷載強度的Gauss白噪聲。

顯然，對于橋梁結構等耗散的Hamilton系統，fik不依賴于p，Wong－Zakai修正項為0，從而珨H＝H，則式（14）等價的Ito隨機微分方程為

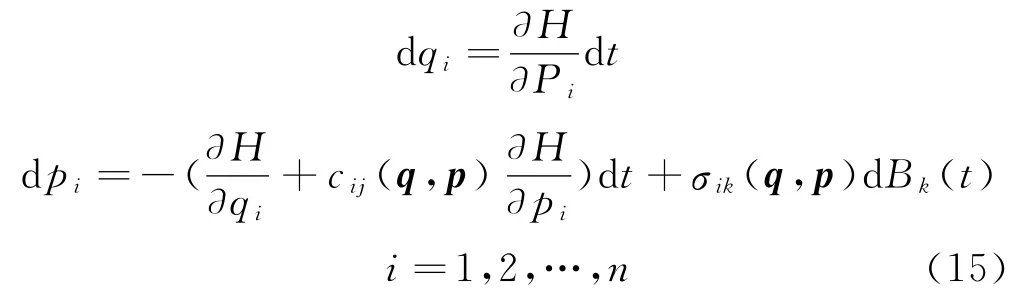
式中：Bk（t）為第k維標準 Wiener過程。

設阻尼力與隨機激勵強度同為ε階小量，即

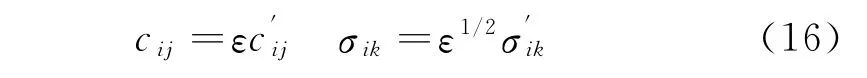
式中：ε 為一正小參數；c′ij、σ′ik為有限量。

式（15）可改寫成

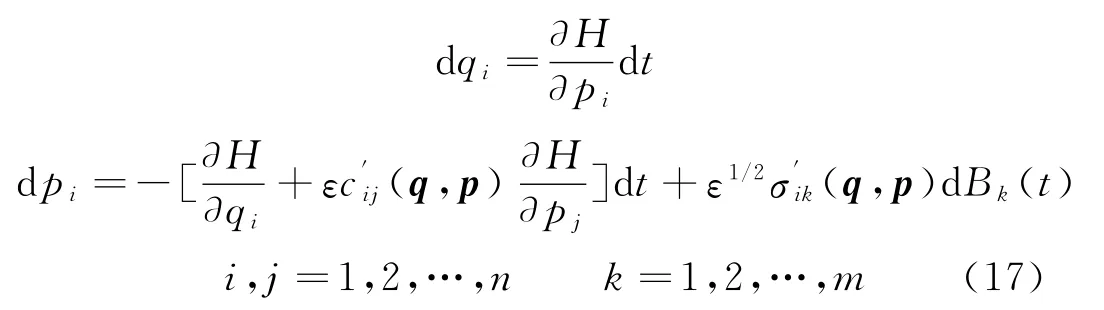
式（17）稱為擬 Hamilton系統，對應于H（q，p）為可積函數的系統稱為擬可積Hamilton系統。

在物理上，只要振動一周，隨機激勵輸入系統的能量與阻尼消耗的能量之差同系統本身能量相比為小，即可視為擬Hamilton系統。

根據以上的等價擬可積Hamilton系統理論，鐵路混凝土橋梁系統的廣義動量、廣義速度、Hamilton函數及擬Hamilton方程為

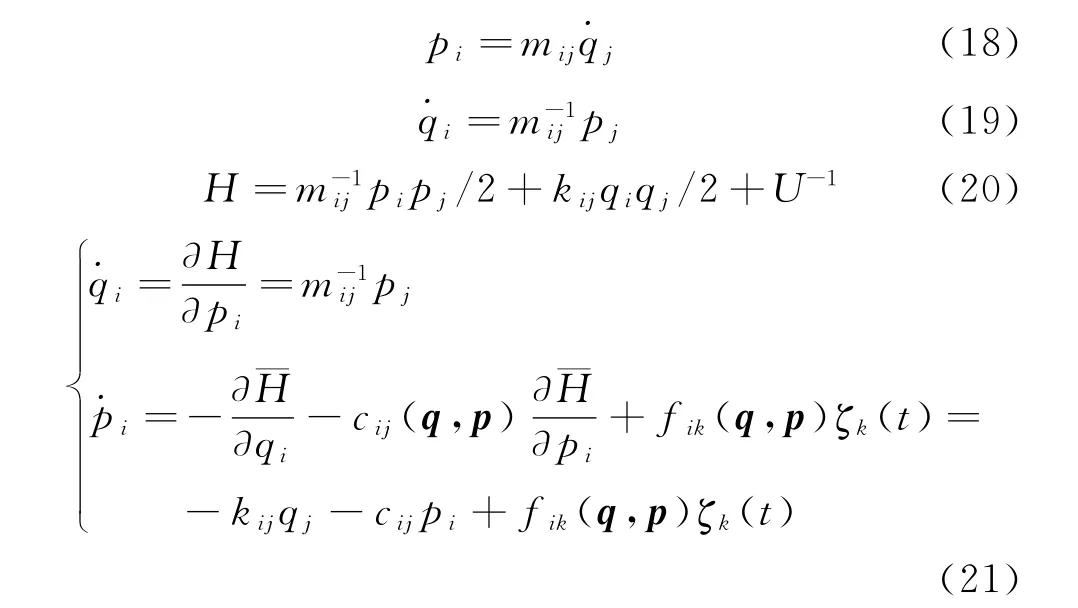
式（18）～式（21）的位移、質量、剛度和阻尼分別為廣義振型坐標、廣義質量、廣義剛度和廣義阻尼。

進一步，將式（4）兩邊同除以第i振型廣義質量Mi，則可得

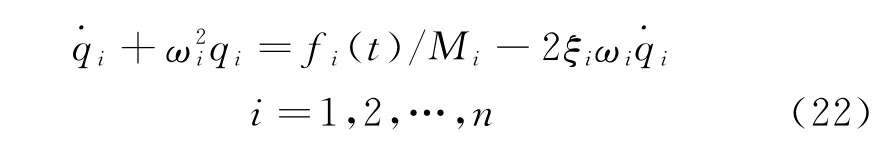
式中：fi（t）＝為第i振型阻尼比；ωi為第i振型相應的頻率。

式（22）所示的振動結構體系，宏觀上可視為各自由度互不耦合的n維單位質量振動體系，該體系對應的廣義質量、廣義阻尼和廣義剛度可分別視為

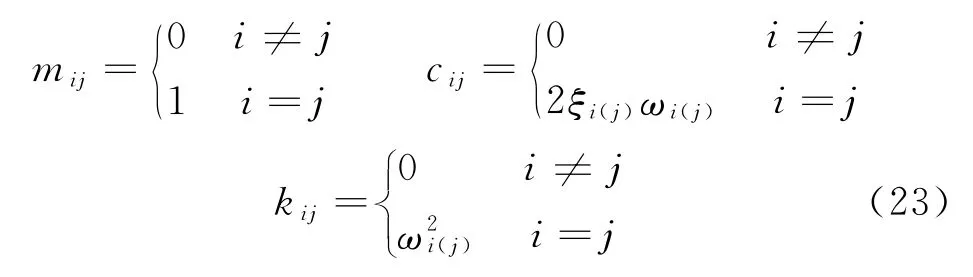
則其對應的廣義動量、廣義速度、Hamilton函數及擬Hamilton方程為

式中：i＝j＝1，2，…，n；k＝1，2，…，m；κi＝fik（q，p）／mi（i＝1，2，…，m）定義為激勵荷載的第i維廣義質量。

由式（26）可看出，該系統相應的Hamilton函數為可積函數，則該系統為擬可積Hamilton系統。

2 既有鐵路混凝土橋梁動力可靠性分析

一般的橋梁結構體系均為連續結構體系，其各階振型可用連續函數表示，取少數幾個起控制作用的振型能準確的反應其振動特性，這就極大的減少了計算Hamilton系統時的位移和動量參數。

此處僅考慮鐵路混凝土橋梁的橫向位移和扭轉位移，并以隨機量（Q，P）代替（q，p），則根據式（27），其運動微分方程為

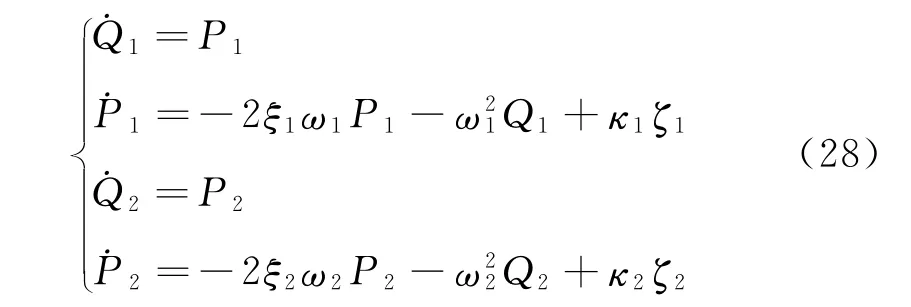
式中：下標1表示橫向位移各參數；下標2表示扭轉位移各參數；ζ1、ζ2分別表示橫向和扭轉激勵源，是強度為 2Di的 獨 立 高 斯 白 噪 聲；κi＝相應的Hamilton函數為H＝H1＋H2，設ωi不滿足共振關系，按文獻［19］中的隨機平均法，可得式（28）的平均Ito方程為［12］

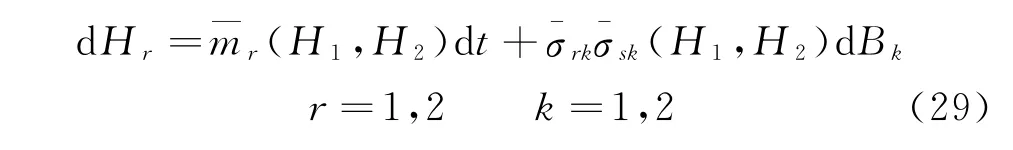
式中（H1，H2）＝－2ξrωrHr＋κrDr；當r＝s時，（H1，H2）＝2κrDrHr，當r≠s時（H1，H2）＝0。根據Ito微分法則，其條件可靠性函數R（t滿足下列后向Kolmogorov方程［12］

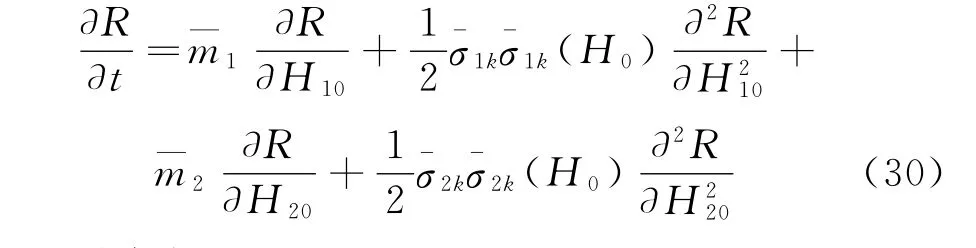
初始條件為

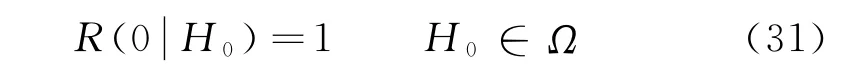
設安全域邊界由Γc和Γ0組成，見圖1，即

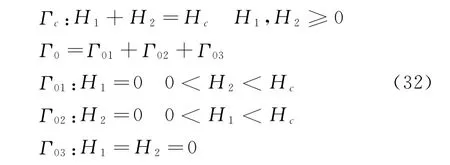
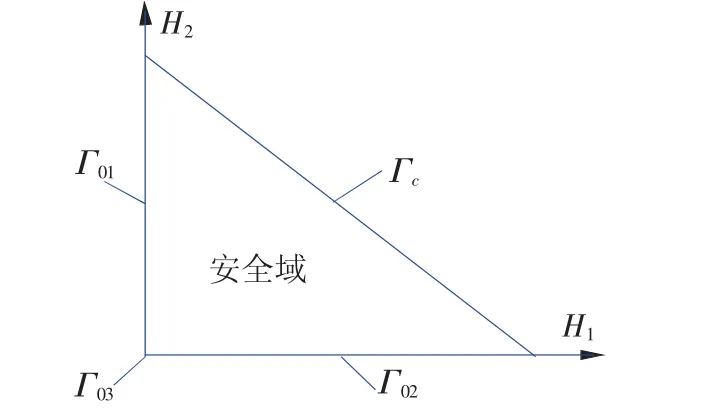
圖1 安全域及其邊界

相應定量邊界條件為

對于上述偏微分方程，可用有限差分法進行數值求解［20］。只考慮在離散能量點 H1i＝iΔH1（i＝0，1，…，N1）、H2j＝jΔH2（i＝0，1，…，N2）和離散事件點的tn＝nΔt（n＝0，1，…）的R的值，H1i、H2j和tn將空間（H1，H2，t）化分成矩形網格，將R 的一階和二階導數用相鄰點的R值表示，代入后向Kolmogorov方程和邊界條件，就能由已知的初值求出任意點在任意時刻的R值。

3 工程算例

西安鐵路局管內陽（平關）—安（康）線于60年代末“三線”建設時期修建，為單線Ⅰ級干線，電力牽引區段，全長351.566km，牽引定數4 000t，通行能力為37.5對／天。線路允許速度100km／h，全線共有橋梁351座／27 221延米；其中圬工橋347座／1 016孔（23.8m跨度預應力圬工梁369孔，31.7m 跨度預應力圬工梁255孔），這兩種跨度的預應力鋼筋混凝土梁圖號分別為“大（65）138”、“叁標外橋006A”、“豐70－1”、“豐70－2”、“叁標橋2019”等。跨度23.8m 的預應力梁ANSYS模型及單片T梁的截面特性分別如圖2（a）和圖2（b）所示（31.7m 的預應力梁模型及截面特性與23.8m梁相似）。

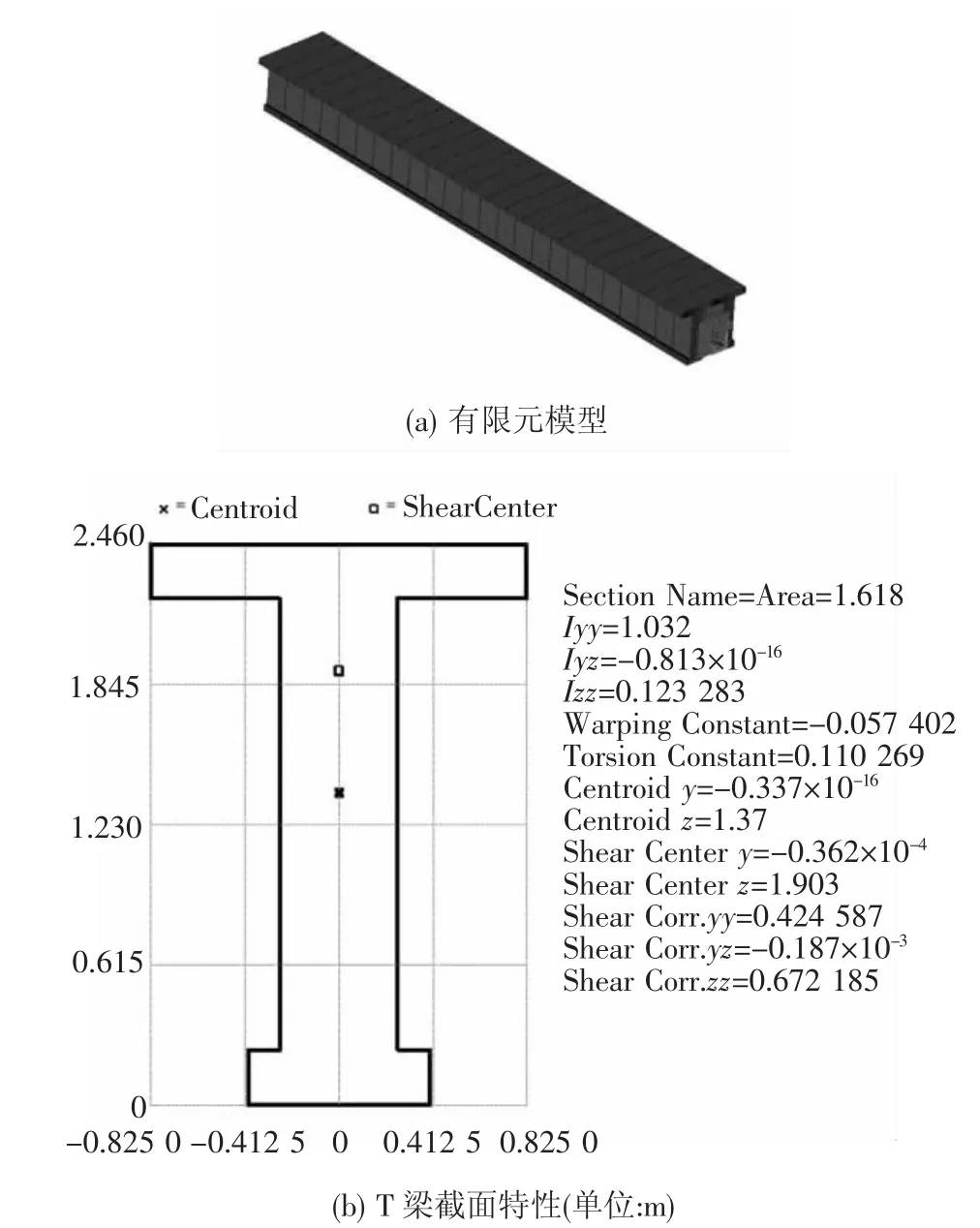
圖2 23.8m梁有限元模型及界面特性

3.1 計算參數的取值

從第2節的分析可看出，在計算橋梁的條件可靠性函數時，需要知道橋梁結構的自振頻率、阻尼比、激勵強度等。對于陽安線混凝土橋梁，阻尼比取最大阻尼比ξ＝0.05［1］；激振源取文獻［1］中隨機模擬的82 km／h的貨車構架加速度蛇形波，強度為D＝σp＝100 cm／s2，文獻［19］中已證明該隨機蛇行波為平穩Gauss過程，此處進一步假設其為Gauss白噪聲過程；一節貨車質量取為80 000kg，每個構架對應的質量取為m車＝40 000kg［21］；參考文獻［1］的研究成果，橋梁橫向和扭轉的一階振型函數取為i（x）＝sinπx／L，m1＝ρAx，m2＝h3m1／3，ρ＝2.6×103kg／m3為混凝土密度，A＝1.618m2為 T 梁截面，h＝2.46m 為 T 梁高度。用有限元計算軟件ANSYS計算出23.8m梁的一階橫向和扭轉頻率分別為4.543Hz和12.277Hz，31.7m梁的一階橫向和扭轉頻率分別為3.036Hz和8.905Hz［17］。用中心有限差分法（邊界處用向前差分法）計算可靠性函數和可靠性概論密度函數時，參照文獻［20］中的精度要求并經必要試算，取N1＝N2＝N＝51（即將H1、H2等分為51份），dt＝0.004（即計算時間間隔為0.004s）。對于橋梁的臨界破壞能量Hc，可根據規范規定的振幅界限、列車脫軌能量界限或橋梁結構破壞能量等不同的依據和計算需要確定。因目前對鐵路橋梁的各種臨界能量并無明確的取值和計算規定，此處所取的臨界能量僅為分析比較之用。

3.2 計算結果分析

用MATLAB編寫程序計算M 文件JS1.m按式（30）求解條件可靠性函數R（t）和轉移概率密度函數p（t）［22］。23.8m梁的計算結果如圖3（a）～3（h）所示。31.7m 梁可靠性函數R（t）、概率密度p（t）與23.8m梁相似，部分圖形如圖4（a）、4（b）所示。

從圖3、圖4中可以看出：

（1）橋梁初始能量越大，則橋梁的可靠性越低；

（2）橋梁的臨界能量Hc1、Hc2越大，則橋梁的可靠性越高，可靠性由Hc1、Hc2共同控制；

（3）橋梁的初始能量越大，則其概率密度的峰值越大，概率密度函數的分布越集中；

（4）橋梁的臨界能量Hc1、Hc2越大，則其概率密度函數的峰值越小，概率密度函數的分布越均勻。

實際情況中，在其他參數（剛度等）相同的情況下，橋梁的初始能量較大，則意味著列車過橋前，橋梁的變形或振動較大，則列車過橋時，橋梁的破壞概率就較大，橋梁的可靠性較低；同樣，橋梁的臨界能量越大，意味著橋梁變形能力越強，橋梁的可靠性越高。

在相同條件下，H10＝H20＝0時23.8m 梁和31.7m梁的可靠性對比見圖5，兩者的可靠性差值見圖6。從圖5和圖6中可看出，在初始能量為零，臨界能量相等的情況下，31.7m梁比23.8m梁的可靠性大，這說明，在其他參數相同的條件下，31.7m梁比23.8m梁的變形能力強，這與結構越柔變形能力越大的力學理論相符。

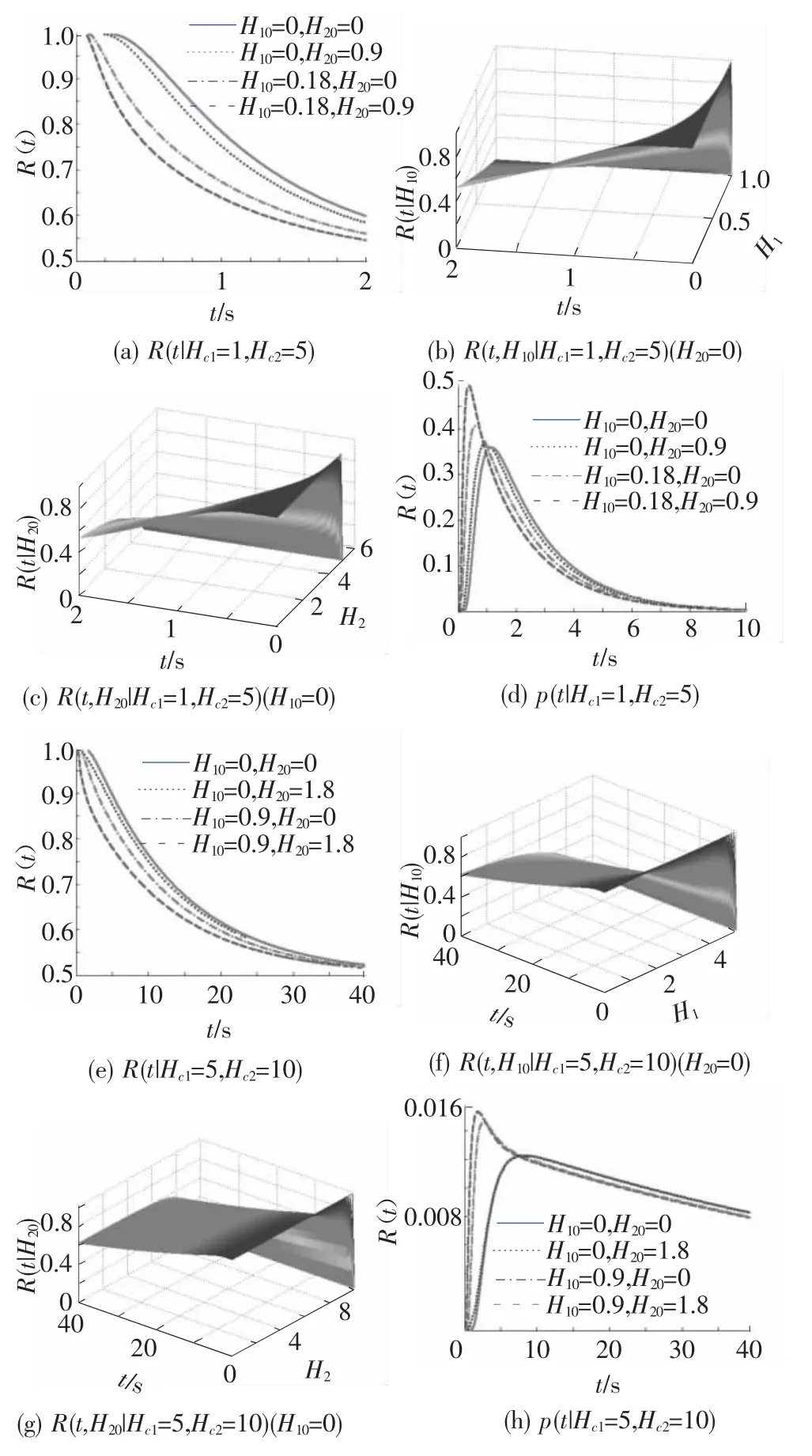
圖3 23.8m梁R(t)和p(t)計算圖

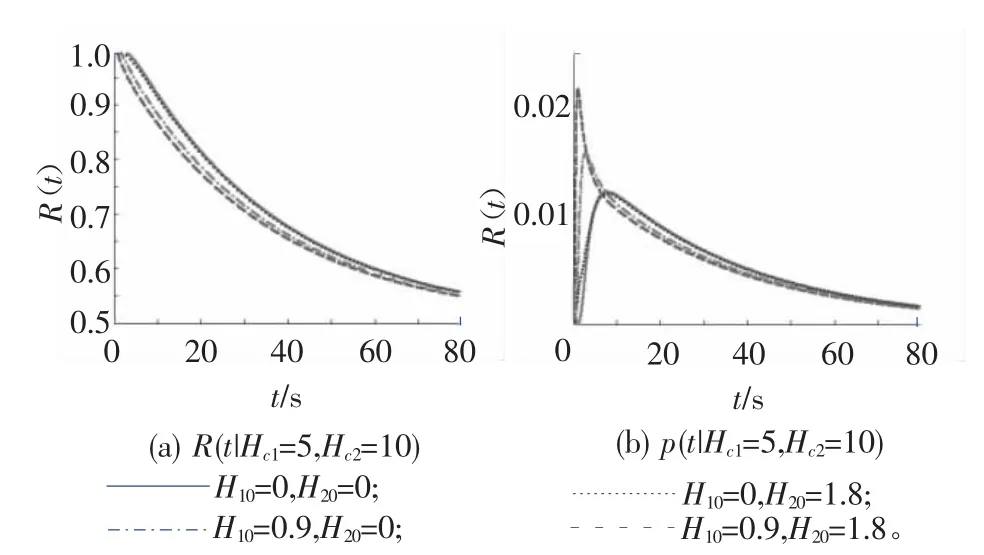
圖4 31.7m梁R(t)和p(t)計算圖

從以上分析可知，基于擬可積Hamilton系統的陽安線混凝土橋梁的動力可靠性函數符合實際情況，說明這種計算方法是合理的。

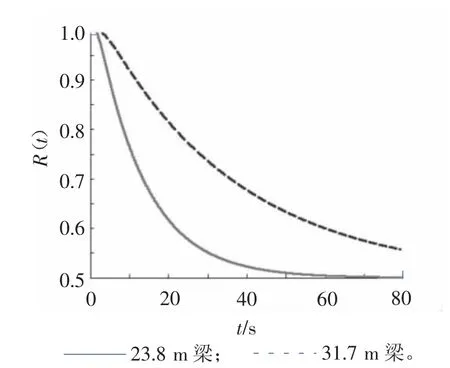
圖5 相同條件下23.8m和31.7m梁R(t|Hc1=5,Hc2=10)對比圖(H10=0,H20=0)

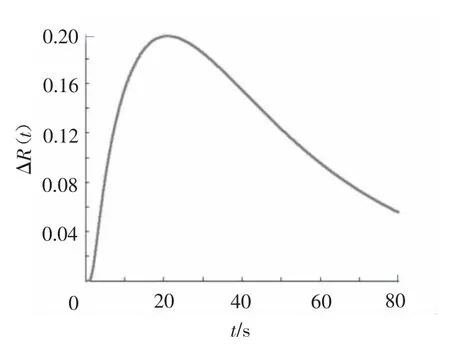
圖6 相同條件下，23.8m和31.7m梁R(t|Hc1=5,Hc2=10)差值圖(H10=0,H20=0)

4 結論

本文通過對擬Hamilton系統理論的研究，基于振型疊加法建立了既有鐵路混凝土橋梁的等價擬可積Hamilton系統方程。通過對此系統方程的分析，得出了鐵路混凝土橋梁在Gauss白噪聲激勵下的條件概論可靠性函數和其定量邊界條件、初值條件，借助MATLAB軟件使得方程求解非常容易。工程算例分析結果表明，該方法對鐵路橋梁的動力可靠性分析是合理的，分析結果和實際情況相符。

參考文獻：

［1］曾慶元，郭向榮.列車橋梁時變系統振動分析理論與應用［M］.北京：中國鐵道出版社，1999.

［2］郭文華，曾慶元.高速鐵路多跨簡支梁橋橫向振動隨機分析［J］.長沙鐵道學院學報，1997，15（1）：1－9.

GUO Wenhua，ZENG Qingyuan.Transverse Random Vibration Analysis for the High－speed Railway Multi－span Simply－supported Bridge［J］.Journal of Changsha Railway University，1997，15（1）：1－9.

［3］劉佩.隨機地震作用下結構動力可靠度計算方法研究［D］.北京：北京交通大學，2010.

［4］LI J，CHEN J B.Stochastic Dynamics of Structures［M］.New York：John Wiley and Sons，2009.

［5］CHEN J B，LI J.A Note on the Principle of Preservation of Probability and Probability Density Evolution Equation［J］.Probabilistic Engineering Mechanics，2009，24（1）：51－59.

［6］RICE S O.Mathematical Analysis of Random Noise［J］.Bell System Technical Journal，1944，23（3）：282－332.

［7］RICE S O.Mathematical Analysis of Random Noise－conclusion［J］.Bell System Technical Journal，1945，24（1）：146－156.

［8］朱位秋.非線性隨機動力學與控制－Hamilton理論體系框架［M］.北京：科學出版社，2004.

［9］ZHU W Q，CAI G Q.Random Vibration of Viscoelastic System under Broad－band Excitations［J］.International Journal of Non－linear Mechanics，2011，46（5）：720－726.

［10］ZHU W Q，CAI G Q.Generation of Non－gaussian Stochastic Processes Using Nonlinear Filters［J］.Probabilistic Engineering Mechanics，2014，36：56－62.

［11］HU R C，YING Z G，ZHU W Q.Stochastic Minimax Optimal Control Strategy for Uncertain Quasi－hamiltonian Systems Using Stochastic Maximum Principle［J］.Structural and Multidisciplinary Optimization，2014，49（1）：69－80.

［12］ZHU W Q，DENG M L，HUANG Z L.First－passage Failure of Quasi－integrable－hamiltonian Systems ［J］.ASME Journal of Applied Mechanics，2002，69（3）：274－282.

［13］CHEN L C，DENG M L，ZHU W Q.First Passage Failure of Quasi Integrable Hamiltonian Systems under Combined Harmonic and White Noise Excitations［J］.Acta Mechanica，2009，206（3－4）：133－148.

［14］CHEN L C，ZHU W Q.Reliability of Quasi Integrable Generalized Hamiltonian Systems［J］.Probabilistic Engineering Mechanics，2010，25（1）：61－66.

［15］LIU W Y，ZHU W Q，JIA W T.Stochastic Stability of Quasi－integrable and Non－resonant Hamiltonian Systems under Parametric Excitations of Combined Gaussian and Poisson White Noises［J］.International Journal of Nonlinear Mechanics，2014，58：191－198.

［16］CLOUGH R W，PENZIEN J.Dynamics of Structures［M］.3rd ed.Berkeley，California：Computers ＆ Structures，Inc.，2003.

［17］赫中營.基于擬Hamilton理論的既有鐵路橋梁動力可靠性研究［D］.蘭州：蘭州交通大學，2008.

［18］陳濱.分析動力學［M］.北京：北京大學出版社，1987.

［19］星谷勝.隨機振動分析［M］.常寶琦，譯.北京：地震出版社，1977.

［20］陸金甫.偏微分方程差分方法［M］.北京：高等教育出版社，1988.

［21］嚴雋耋.車輛工程［M］.北京：中國鐵道出版社，2003.

［22］劉衛國.MATLAB程序設計教程［M］.北京：中國水利水電出版社，2005.