基于不確定客流的高速鐵路列車停站方案優化方法
牛 豐, 戚建國, 秦 進
(1. 中南大學 交通運輸工程學院,湖南 長沙 410075; 2. 中國鐵路總公司,北京 100844;3. 北京交通大學 軌道交通控制與安全國家重點實驗室,北京 100044)
列車停站方案是列車開行方案的重要環節,明確列車為旅客提供的服務區間,在列車徑路、類別、編組輛數、開行頻率確定后,根據客流需求和列車協調配合情況確定各類列車的停站序列[1]。列車停站方案的設置不僅關系到高速鐵路的服務質量,而且對于鐵路資源的利用效率和經濟效益也具有重要影響。
鑒于列車停站方案的重要性,諸多學者針對該問題進行一系列頗有成效的研究。目前,大多數文獻將列車停站方案與開行方案的其他子問題一并進行研究[1-2]。文獻[1]通過分析列車停站設置和客流換乘選擇之間的博弈關系,將基于停站方案的多類用戶均衡客流分配模型作為下層規劃模型,構建旅客列車停站方案雙層規劃模型,并設計基于模擬退火算法的啟發式算法對模型進行求解;文獻[2]將高速鐵路系統包含的不確定性和不易量化因素統一用節點服務表示,以節點服務頻率、站間服務可達性、單個列車停站次數等作為主要約束條件,構建以總停站次數最少為目標的非線性規劃模型,運用停站概率與計算機模擬相結合的方法有效解決模型求解的問題;文獻[3]將列車停站次數及相應的停靠車站嵌入列車開行方案中,建立以最小化旅客停站時間、列車虛糜及未滿足需求的旅客數量為目標的多目標多層0-1整數規劃模型,利用有序組合樹方法對模型求解;文獻[4]基于區段最大客流密度確定所需最少開行列車數量,提出基于停站方案的旅客列車開行方案優化策略;文獻[5]分析列車停站的主要影響因素,從方便旅客出行及減少旅客出行廣義費用兩方面考慮,建立列車停站方案綜合優化模型,并結合列車停站優化問題的具體特點,提出包含初步和綜合優化的兩階段優化算法對模型求解;文獻[6]分析高速鐵路停站方案對列車牽引能耗和旅行時間的影響,以最小列車牽引能耗和最短旅行時間為優化目標,以既有運輸供給為約束,建立考慮列車能耗的既有停站方案優化模型;文獻[7]分析列車停站與時刻表之間的相互關系,構建列車停站方案與運行圖協同優化模型;文獻[8-13]對運行圖及運行圖追蹤進行詳細論述。
上述文獻為探討高速鐵路列車停站方案優化設計方法提供良好的理論基礎,但現有研究大多在確定的環境下考慮列車運行組織優化問題,而對停站方案設計中一些不確定因素未能給予充分考慮。實際上,由于旅客出行目的的多樣性以及線路上各車站所處地理位置及政治地位的不同,每天乘坐列車出行的旅客明顯不同,導致同1條線路上不同車站之間的客流亦有很大差異,從而致使車站上發送、到達客流量具有很大的不確定性。以京滬線泰安站為例, 某3個月的發到客流分布情況見圖1。
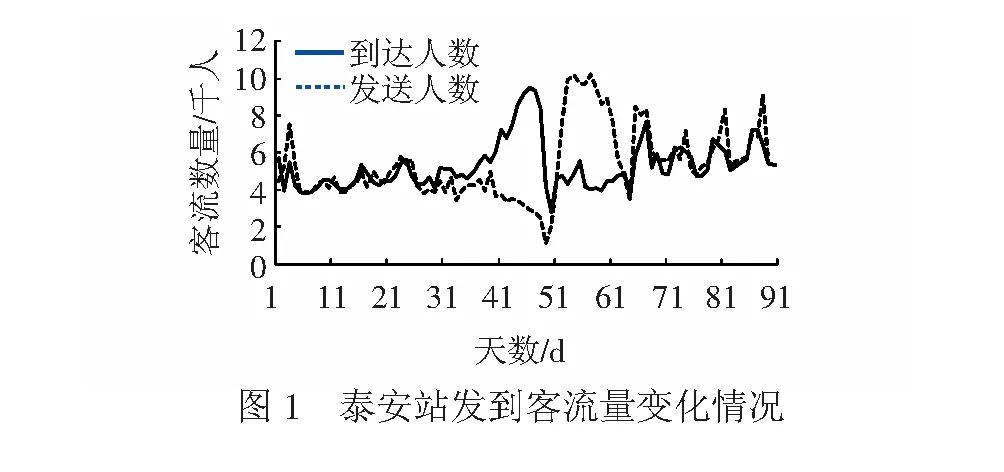
從圖1可以明顯看到,發到客流量隨著時間不同而不斷波動,且很難用概率論和數理統計的方法刻畫其規律性。車站發到客流隨時間變化的波動性和無規律性直接導致車站發到客流量的不確定性。
確定環境下的列車停站優化模型,只是針對某種情況下客流需求優化列車停站策略,難以應對客流需求不斷波動情況下的優化決策。忽略鐵路運營中客流的不確定性勢必導致某些時段內列車有較大虛糜或突發客流需求不能得到滿足的情況,從而導致服務水平和運輸資源利用效率的降低。因此,探討基于不確定客流的高速列車停站方案的優化設計,對提高列車服務的魯棒性和可靠性,規避不確定因素帶來的決策風險具有重要的理論和現實意義。
本文擬在既有研究的基礎上,從理論研究的角度出發,將高鐵車站的發到客流需求描述為不確定變量,構建高速鐵路列車停站方案優化問題的機會約束規劃模型,并進一步基于不確定理論和方法,將該模型轉化為確定的等價類模型后進行求解和計算。
1 問題描述
設圖2為某高速鐵路線路,S表示線路上車站的集合, |S|表示車站數量。該線各站從左至右依次編號為1,2,3,…,|S|。其中,車站1代表起始站,車站|S|代表終點站,其余編號代表線路中間車站。T表示給定開行方案下運行在該線路上的列車集合,|T|為列車開行列數。下面研究如何合理確定在區段上開行的所有列車的停站方案,要求在盡可能滿足客流需求和保障一定服務水平的基礎上,優化高速鐵路運輸資源利用效率。

高速鐵路客流需求一直呈現出高度的不確定性。當具備充足的歷史數據時,可以考慮采用數理統計方法,將客流需求處理為服從一定概率分布的隨機變量;而在缺乏充足樣本的情況下,有效的描述方法是將該類數據視為不確定變量進行分析。本文正是基于不確定理論的相關方法,將各車站的發到客流數據處理為不確定變量,建立數學優化模型進行分析。
2 模型構建
2.1 模型決策變量
為清楚的確定列車在每個車站的停站方案,采用如下決策變量確定列車k的停站策略
式中:k、i分別為列車與車站的標號,且k∈T,i∈S。
2.2 模型目標函數
高速鐵路列車停站方案對線路的通過能力和運輸效率產生較大影響。一般而言,增加列車停站次數將延長列車占用車底的時間,從而增加運營所需的總車底數量、列車因啟制動引起的額外能耗、乘務組費用以及車站的額外費用等[3]。因此,在滿足旅客需求置信水平的前提下,盡量減少列車停站次數,可以降低運輸成本,提高鐵路企業經濟效益。本文將以最小化列車總停站次數為優化目標,以期用最少的運營成本(即停站次數)滿足一定置信水平下的不確定旅客需求。
模型優化目標為
( 1 )
式中:X為決策變量xki組成的向量;F(X)為所有列車總停站次數。
2.3 模型約束條件
列車停站方案必須盡可能滿足鐵路運輸需求并符合相關技術規范。因此,在編制過程中需要考慮一系列系統約束條件,如客流需求約束、停站次數約束等。
(1) 車站發送和接收客流約束
高速鐵路運營中,旅客出行目的多樣性導致車站發到客流需求的無規律波動。對于車站發到客流量的不確定性,本文將其描述為不確定變量,并采用不確定分布函數進行有效刻畫。在此基礎上,采用機會約束規劃思想,將滿足客流需求表示為發到客流需求得到滿足的機會達到一定的置信水平,以獲得魯棒性較強的列車停站方案。發到客流需求滿足的置信水平約束可分別表示為
?i∈S
( 2 )
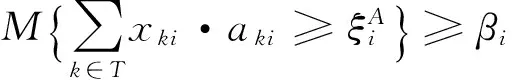
( 3 )
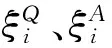
車站發送和到達客流約束是本文模型中最重要的約束條件,也是列車停站方案中首要考慮的因素。其中,約束條件(2)確保每個車站i的旅客發送能力大于該車站客流需求的不確定測度大于給定的置信水平αi;約束條件(3)保證每個車站i接收旅客的能力大于該車站客流需求的不確定測度大于給定的置信水平βi。
(2) 車站所需最少停靠列車數量約束
優化列車停站方案的過程中,若僅考慮各車站發送和接收客流需求約束,則可能導致客流較小的車站停靠列車數量過少。為進一步提高客流需求較小車站旅客出行的便捷性,體現鐵路運營的公共服務特點,規定每個車站的最小停站列車數量,以保障車站必要的服務水平,即
?i∈S
( 4 )
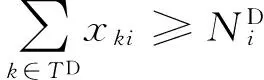
( 5 )
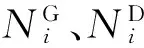
該約束條件可確保每個車站停靠的不同速度列車數量不小于事先確定的閾值。事實上,盡管該約束可能將增加某些列車的停站次數,延長旅客的出行時間,但也最大限度提高鐵路服務的均衡性及短途旅客出行的便捷性。
(3) 列車最大停站次數約束
列車停站次數對運輸能力和運輸效率具有重要影響,停靠較多車站必然將延長列車對車底的占用,大幅度增加列車的總運行時間,降低線路的通過能力。此外,頻繁的停站操作也將導致列車不斷地啟動和制動,產生不必要的能源消耗。從運輸服務水平和舒適性方面看,旅客期望在出行過程中盡可能停靠較少的車站,以減少總旅行時間。基于以上分析,模型需要對列車的總停靠次數進行約束。
最大停站次數約束
?k∈T
( 6 )
式中:Mk為列車k允許的最大停站數量。
顯然,該約束確保列車總的停站次數在預先給定的范圍之內,從而避免某些列車停靠車站較多(特別是速度等級較高的列車),而另外一些列車停站較少的現象,保證高速鐵路運輸系統中列車服務的均衡性。
(4) 開行區段約束
實際運營中,由于給定區段內開行的列車不經過該區段以外的其他車站,且給定區段內的所有列車必須從該運行區段的起始車站行至終到車站。
開行區段約束
?k∈T
( 7 )
xkSk=xkRk=1 ?k∈T
( 8 )
式中:Lk為列車k開行區段內車站集合,Lk∈S;Sk、Rk分別為列車k在其開行區段內的起始和終到車站。
上述約束保證所有列車按照開行方案中預先設定的開行區段運行,同時不經過既定服務區段之外的車站。
(5) 變量取值約束
變量xki為0-1決策變量,取值約束為
xki∈{0,1} ?k∈T?i∈S
( 9 )
2.4 建立模型
根據以上分析,構建基于不確定客流的高速鐵路列車停站方案優化模型
(10)
s.t.
?i∈S
(11)
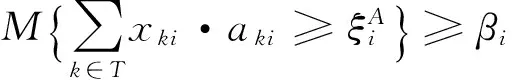
(12)
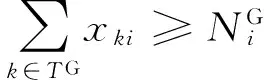
(13)
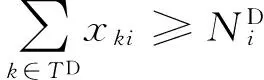
(14)
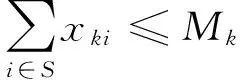
(15)
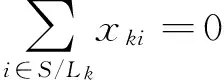
(16)
xkSk=xkRk=1 ?k∈T
(17)
xki∈{0,1} ?k∈T?i∈S
(18)
3 確定性等價類模型
3.1 不確定理論及其定義
不確定理論為有效處理難以獲取精確信息的不確定決策問題提供良好的數學基礎,已被成功應用于多個實際領域,如交通運輸領域[14]、金融領域[15]和圖論領域[16]等。為便于后續分析和闡述,下面簡要介紹不確定理論中的部分定義、公理及推論。
定義1不確定測度
假設Γ為非空集合,L是Γ上的σ-代數。每個元素Λ∈L被稱為1個事件,M{Λ}表示事件Λ發生的置信水平。如果M{Λ}滿足以下3條公理,則稱為不確定測度[17]。
(1) 常規性:對于全集Γ,有M{Γ}=1;
(2) 自對偶性:對于任意事件Λ,有M{Λ}+M{Λc}=1。其中,Λc為Λ的對立事件;
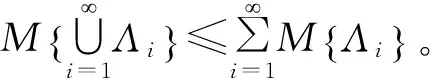
事實上,不確定測度可理解為不確定事件發生的信度,而不是頻率,他取決于每個人對該事件的認知程度,具有一定的主觀性。
定義2不確定空間
假設Γ為非空集合,L為Γ上的σ-代數,M為不確定測度,則稱三元組M(Γ,L,M)為不確定空間[17]。
定義3不確定變量
不確定變量ξ是從不確定空間(Γ,L,M)到實數集的1個可測函數。即對任意實數Borel集B,集合{ξ∈B}={γ∈Γ|ξ(γ)∈B}是L中的1個事件[17]。
不確定空間和不確定變量的定義與概率論中的概率空間和隨機變量的定義形式類似。但由于不確定測度與概率測度有本質區別,不確定變量的內涵也不同于隨機變量。
定義4不確定分布
不確定變量ξ的不確定分布Φ定義為Φ(x)=M{ξ≤x}。其中,x為任意實數[17]。
定義5常規不確定分布
如果1個不確定分布的逆函數Φ-1(α)對于任意的α∈(0,1)存在且唯一,則稱該不確定分布為常規不確定分布[17]。
定義6逆不確定分布
假設不確定變量ξ服從常規的不確定分布Φ(x),則稱逆函數Φ-1(x)為不確定變量ξ的逆不確定分布[17]。
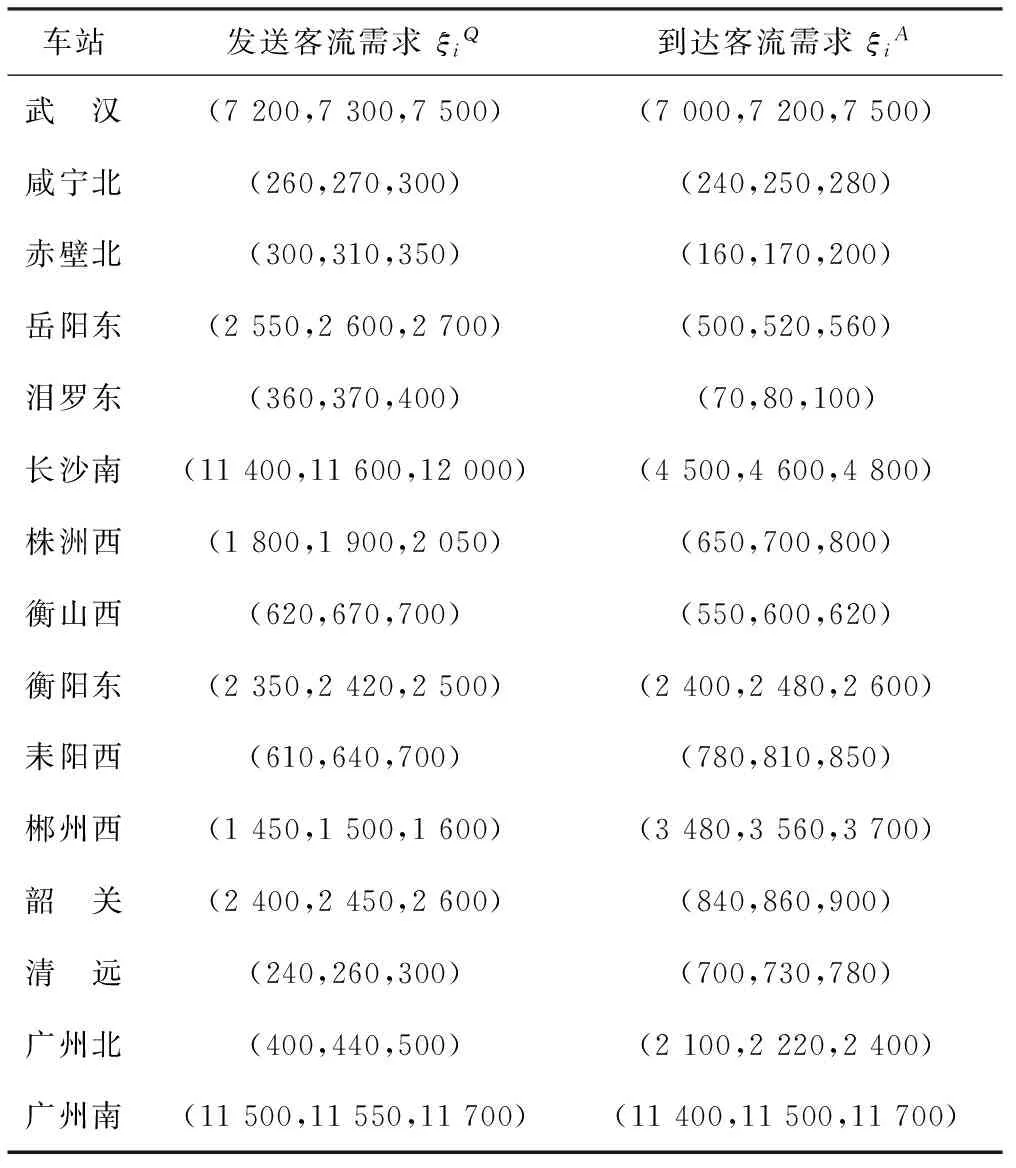
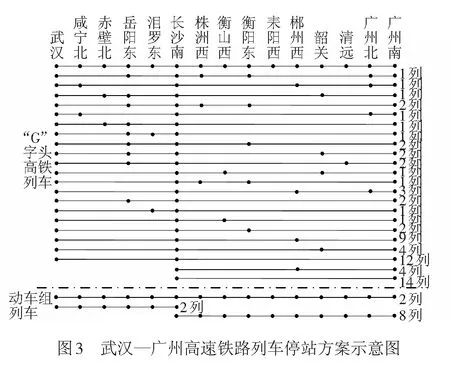
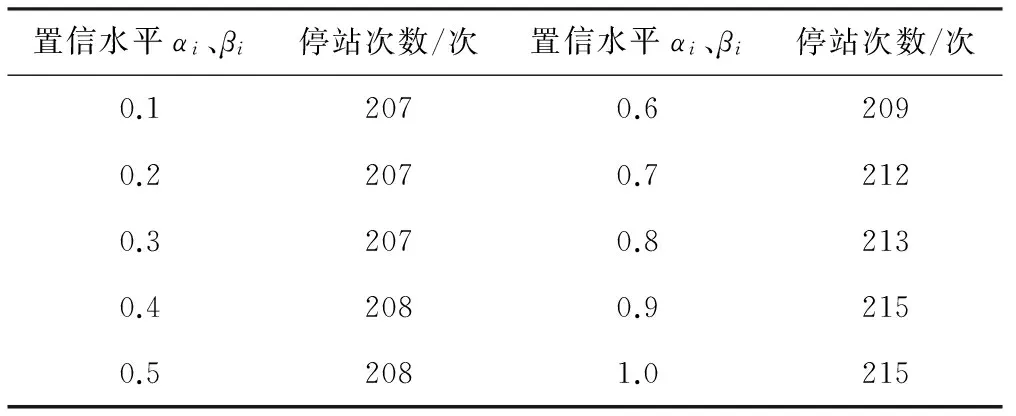
在決策過程中,可以采用不確定分布的形式刻畫任意的不確定變量。如果不確定變量ξ的不確定分布如下所示,則稱ξ為之字形不確定變量,記為Z(a,b,c)。其中,a、b、c為實數且滿足a (19) 顯然,之字形不確定變量的不確定分布為分段函數形式,其中每段圖像均為線性函數。在實際應用中,之字形不確定變量是較為常用的非精確數據的表示方式[17]。 定義7關鍵值 假設ξ為不確定變量,且α∈(0,1],則稱ξsup(α)=sup{r|M{ξ≥r}≥α}為ξ的α-樂觀值;ξinf(α)=inf{r|M{ξ≤r}≥α}為ξ的α-悲觀值[17]。 下面,重點介紹2個機會約束的等價定理,相關結論對于構建機會約束規劃模型的等價類起著關鍵的作用。 推論1之字形不確定變量Z(a,b,c)的逆不確定分布為[17] Φ-1(α)= 利用上述定義、定理及推論,將本文前面提出的不確定客流下高速鐵路列車停站方案的機會約束規劃模型轉化為確定性等價類模型,以便于模型的求解和計算分析。 ?i∈S (20) (21) 當且僅當 ?i∈S (22) (23) (24) (25) 基于以上分析,將前面提出的機會約束規劃模型式(10)~式(18),重新構建為0-1整數線性規劃模型 s.t. 式(13)~式(18)、式(22)~式(23) 與原模型式(10)~式(18)相比,上述線性模型的目標函數和約束條件均不變,僅原模型中的置信水平約束(11)~約束(12)被替換為線性約束(22)~約束(23),由此模型中的所有約束條件均為線性表達式。上述線性模型可直接通過MATLAB調用GUROBI優化軟件進行求解。 上述模型中置信水平αi和βi為預設參數,其值的選取是由決策者預先給定。樂觀決策者可設定較小的參數,而悲觀決策者則需選取較大參數以保證約束在較高置信水平下成立。此外,對于該參數的選擇,可給出如下定理: 證明:假設D′和D*分別為兩組參數可行解的集合。由于對任意X∈D*,有 ?i∈S (26) (27) 從而說明D′?D*成立。可得以下結論 (28) 定理得證。 以武漢—廣州段高速鐵路為背景,假設列車開行對數和開行區間已知的條件下,應用構建的模型優化確定列車停站方案。 為簡化問題,僅考慮從武漢到廣州的單向線路,共15個車站、開行80列列車。根據客流需求,整個線路劃分為3個區段,即武漢—廣州南、武漢—長沙南、長沙南—廣州南。其中,武漢到廣州南開行50列高速鐵路動車組列車(G字頭列車)和2列動車組列車(D字頭列車),武漢到長沙南開行2列D字頭列車,長沙南到廣州南開行18列G字頭列車和8列D字頭列車。簡單起見,對于各類列車的發送和接收旅客能力,假定每一列車在各車站的發送和接收旅客能力相同,均設定為150人,同時,對于車站發送和到達旅客需求得到滿足的置信水平均設置為90%。 對于列車停站次數,設定高速鐵路動車組列車的最大停站次數為10次,動車組列車為站站停列車。為保障沿線客流需求較小車站的服務水平,假定每站至少需有2列G字頭列車停靠。 考慮到高速鐵路實際運營過程的復雜性,各站發送和到達旅客需求服從的分布形式及具體數值,一般由相關專家根據經驗給出。為數據處理方便,本文將其設定為服從之字形分布的不確定變量,見表1。 表1 車站發送和到達客流需求 人 將所建模型轉化為確定等價類模型后,在CPU為I3-4130、內存為4 G的Windows 7系統中,使用MATLAB調用GUROBI優化軟件對模型求解,計算時間均不大于1 s。 在滿足各站客流需求的不確定測度均大于90%的條件下,可得到列車停站方案,見圖3。 從圖3可以看出,除起始和終到車站外,該停站方案中所有列車共停站215次。由于動車組列車為站站停列車,且每個車站均至少有2列G字頭列車停靠,保證旅客需求較少車站的服務水平。此外,在該停站方案中,大部分高速鐵路動車組列車停站次數相對較少,從而減少旅客在車站等待時間,縮短長距離出行旅客的總出行時間,有效提高直達率。 αi、βi,i∈S為預先確定的服務置信水平,不同的置信水平對應于不同的旅客出行需求滿足程度。為探討不同置信水平的取值對列車停站方案的影響,本文設定αi、βi分別為0.1、0.2、…、1.0,并對模型進行求解,結果見表2。 表2 不同置信水平的列車停站次數 由計算結果可知,隨著不確定置信水平αi、βi的增加,列車在除起始和終到車站外停靠車站的數量呈現上升趨勢以保證更多的旅客需求得到滿足。特別當αi、βi取值為0.1時,列車在車站外最優停站次數為207次,而當αi、βi取值為1.0時,最優停站次數則增加到215次。一般而言,較大的置信水平將滿足更多的旅客需求,相應的停站次數也將增加,運營過程中列車的虛糜也可能增大;相反,較小的置信水平則可能導致較多的客流需求不能被滿足,從而降低旅客的滿意度。另外,列車停站次數的變化亦與給定各站發送和到達旅客需求服從的分布形式及具體數值有關。較大的分布區間,表明客流需求具有更強的不確定性,導致隨著給定置信水平的變化,列車停站次數的變化更為明顯;反之,則變化較小。為此,在實際應用中αi和βi取值應由決策者依具體情況合理選擇。 本文將車站的發到客流量處理為不確定變量,構建不確定客流需求下的高速鐵路列車停站方案問題的機會約束規劃模型,并進一步基于不確定理論的相關知識將其轉化為確定的等價類模型,在此基礎上利用GUROBI優化軟件模型求解。最后,通過武漢—廣州段高速鐵路數據進行驗證。結果顯示,模型及算法具有良好的優化質量和計算效率。 實際運營中,列車停站方案的設計與旅客出行選擇之間存在相互影響,且乘務組排班計劃、時刻表的優化等問題與停站方案之間也存在必然聯系。因此,如何將這些問題與列車停站方案結合為一體進行優化將是下一步研究的主攻方向;其次,列車停站優化模型中考慮OD客流需求以及每列車上客流的分配也是需重點思考的問題;另外,列車停站方案優化問題本質上為多目標決策問題,進一步探討列車能耗、滿載率以及旅客舒適度、可達性等指標也將是今后研究的主要內容。 參考文獻: [1] 鄧連波,史峰,周文梁.旅客列車停站設置方案優化[J].中國鐵道科學,2009,30(4):103-107. DENG Lianbo, SHI Feng, ZHOU Wenliang. Stop Schedule Plan Optimization for Passenger Train[J]. China Railway Science, 2009, 30(4): 103-107. [2] 李得偉,韓寶明,李曉娟,等.基于節點服務的高速鐵路列車停站方案優化模型[J].鐵道學報, 2013, 35(6): 1-5. LI Dewei, HAN Baoming, LI Xiaojuan, et al. High-speed Railway Stopping Schedule Optimization Model Based on Node Service[J]. Journal of the China Railway Society, 2013, 35(6): 1-5. [3] 張擁軍, 任民, 杜文. 高速列車開行方案研究[J]. 西南交通大學學報, 1998, 33(4): 400-404. ZHANG Yongjun,REN Min,DU Wen.Optimization of High Speed Train Operation[J].Journal of Southwest Jiaotong University, 1998, 33(4): 400-404. [4] 漆昕, 熊堅. 基于停站方案的旅客列車開行方案優化研究[J]. 鐵道運輸與經濟, 2012, 34(12): 43-57. QI Xin, XIONG Jian.Research on Optimization of Passenger Train Operation Diagram Based on Stopping Diagram[J]. Railway Transport and Economy, 2012, 34(12): 43-57. [5] 黃鑒, 彭其淵. 高速列車停站優化問題的兩階段求解算[J].西南交通大學學報, 2012, 47(3): 484-489. HUANG Jian, PENG Qiyuan.Two-stage Optimization Algorithm for Stop Schedule Plan of High-speed Train[J]. Journal of Southwest Jiaotong University, 2012, 47(3): 484-489. [6] 馮旭杰, 孫全欣, 馮佳,等. 高速鐵路既有停站方案優化模型[J]. 交通運輸工程學報, 2013, 13(1): 84-90. FENG Xujie, SUN Quanxin, FENG Jia, et al. Optimization Model of Existing Stop Schedule for High-speed Railway[J]. Journal of Traffic and Transportation Engineering 2013, 13(1): 84-90. [7] YANG Lixing, QI Jianguo, LI Shukai, et al. Collaborative Optimization for Train Scheduling and Train Stop Planning on High-speed Railways[J/OL]. Omega, http://dx.doi.org/10.1016/j.omega.2015.11. 003. [8] YANG Lixing, LI Keping,GAO Ziyou. Train Timetable Problem on a Single-line Railway with Fuzzy Passenger Demand[J]. IEEE Transactions on Fuzzy Systems 2009, 17(3): 617-629. [9] YANG Lixing, LI Keping, GAO Ziyou, et al. Optimizing Trains Movement on a Railway Network[J]. Omega,2012, 40: 619-633. [10] YANG Lixing, ZHOU Xuesong, GAO Ziyou. Credibility-based Rescheduling Model in a Double-track Railway Network: a Fuzzy Reliable Optimization Approach[J]. Omega,2014, 48: 75-93. [11] LI Shukai, YANG Lixing, LI Keping, et al. Robust Sample-data Cruise Control Scheduling of High-speed Trains[J]. Transportation Research Part C: Emerging Technologies,2014, 46: 274-283. [12] LI Shukai, YANG Lixing, GAO Ziyou. Coordinated Cruise Control for High-speed Trains Movements Based on a Multi-agent Model[J]. Transportation Research Part C: Emerging Technologies,2015, 56: 281-292. [13] LI Shukai, YANG Lixing, GAO Ziyou. Adaptive Coordinated Control of Multiple High-speed Trains with Input Saturation[J]. Nonlinear Dynamics,2016,83(4):2 157-2 169. [14] YANG Lixing, LIU Pei, LI Shukai, et al. Reduction Methods of Type-2 Uncertain Variables and Their Applications to Solid Transportation Problem[J]. Information Science, 2015, 291: 204-237. [15] CHEN Xiaowei. American Option Pricing Formula for Uncertain Financial Market[J]. International Journal of Operations Research, 2011, 8(2): 32-37. [16] GAO Yuan, YANG Lixing, LI Shukai. On Distribution Function of the Diameter in Uncertain Graph[J]. Information Science, 2015, 296: 61-74. [17] LIU Baoding. Uncertainty Theory[M]. Berlin: Springer-verlag, 2007: 11-114.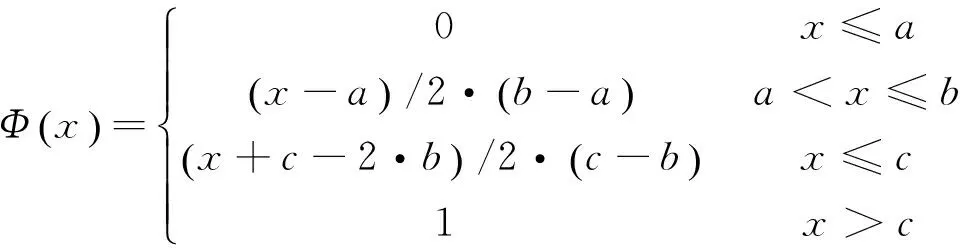
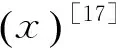
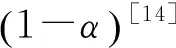
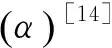
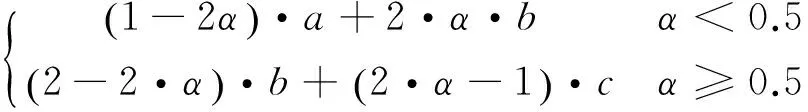
3.2 確定性等價類模型
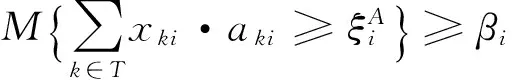
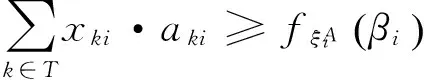
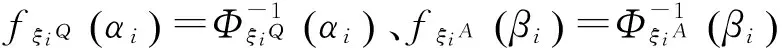
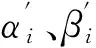
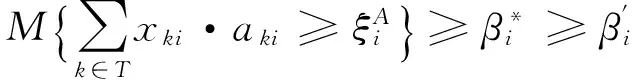
4 算例計算及分析
4.1 模型輸入數據
4.2 停站方案計算分析
4.3 停站次數的靈敏度分析
5 結束語

