基于動態稀疏保局投影的故障檢測方法

鄭鑫，田學民，張漢元（中國石油大學（華東）信息與控制工程學院，山東 青島 266580）

?

基于動態稀疏保局投影的故障檢測方法

鄭鑫，田學民，張漢元
（中國石油大學（華東）信息與控制工程學院，山東 青島 266580）

摘要：針對保局投影（locality preserving projections，LPP）沒有考慮過程數據的全局信息和動態性的問題，提出一種新的基于動態稀疏保局投影（dynamic sparse locality preserving projections，DSLPP）的故障檢測方法。該方法首先將原始數據矩陣擴展為考慮時序相關的增廣矩陣，然后通過求解最優稀疏表示（sparse representation，SR）問題，得到能夠表示數據全局稀疏重構關系的稀疏系數矩陣，并將其與LPP算法結合，構建綜合考慮數據局部和全局關系的目標函數進行數據降維，最后分別在特征空間和殘差空間構造T2統計量和Q統計量進行故障檢測。TEP的仿真結果表明，與LPP方法相比，新方法能更迅速檢測故障發生并降低過程監控漏報率。

關鍵詞：故障檢測；保局投影；稀疏表示；特征提取；過程監控

2015-11-26收到初稿，2015-12-07收到修改稿。

聯系人：田學民。第一作者：鄭鑫（1990—），男，碩士研究生。

引 言

現代化工生產過程日益趨于大型化、集成化、復雜化，設備運行過程中產生了大量高維復雜數據，為了更好地監控過程的運行狀態，需要使用有效的降維技術以及相應的過程監控方法[1]。傳統的主元分析（PCA）和偏最小二乘（PLS）已經在工業過程中應用廣泛[2-4]。針對數據的非線性問題，文獻[5]提出了基于PCA的非線性算法KPCA，取得了良好的效果。近年來的研究表明，流形學習能夠有效地發現隱含在高維數據集中的低維特征[6-8]，該方法假設所處理的數據采樣于一個潛在的低維流形上，通過學習和發現嵌入在高維空間中的低維流形特性，可以有效地揭示數據的結構特征。保局投影（locality preserving projections，LPP）是一種經典的流形學習算法[9]，在降維時能夠較好地保持數據的局部結構信息，Hu等[10]將其應用于間歇過程的故障檢測，取得了較好的效果，但是LPP方法忽略了數據的全局信息[11]，可能導致原始樣本空間中距離較遠的樣本點的低維投影發生重疊，從而破壞數據的本質結構特征。

近年來，稀疏表示（sparse representation，SR）理論成為信號處理、統計學分析和模式識別領域的研究熱點[12-14]。稀疏表示采用一個稱之為字典的超完備冗余基本信號系統，對原始信號進行稀疏線性表示，得到能夠表示原始數據全局稀疏重構關系的稀疏系數矩陣。稀疏系數矩陣可以反映數據的本質幾何特性，并包含自然的鑒別信息，稀疏規則化可自動學習去掉對輸出沒有貢獻的變量，完成特征選擇。

本文針對保局投影應用于故障檢測時沒有考慮過程數據的全局信息和動態性的問題，結合保局投影和稀疏表示，并進一步考慮過程數據的動態性，提出了一種基于動態稀疏保局投影（dynamic sparse locality preserving projections，DSLPP）的故障檢測方法。該方法首先考慮過程數據時序相關的特點，將原始數據矩陣擴展為時滯增廣矩陣形式，然后通過求解L1范數最優值問題，得到能夠表示數據全局稀疏重構關系的稀疏系數矩陣，并將其融入到LPP的目標函數中，構建綜合考慮數據局部和全局關系的目標函數進行數據降維，最后分別構造T2統計量和Q統計量進行故障檢測。TEP的仿真結果驗證了新方法的有效性。

1 保局投影

LPP算法通過優化如下目標函數獲得投影矩陣，保證低維嵌入坐標yi與yj之間的距離最小。

并引入約束

其中，n是樣本數，a為投影向量，L= D? W， D是n× n的對角陣，對角線元素，W是關系矩陣，可通過k近鄰法求得。

則投影向量可通過求解式（4）的廣義特征值問題獲得

最小的d個廣義特征值所對應的特征向量構成了投影矩陣ALPP。

2 動態稀疏保局投影

2.1 稀疏表示

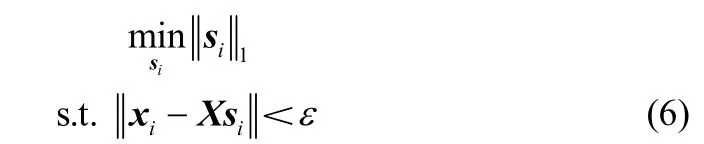
其中，ε為誤差容忍度。該目標函數通過線性規劃求解每一個xi對應的稀疏系數向量si，得到稀疏系數矩陣。

2.2 稀疏保局投影

LPP 算法使原始數據之間的近鄰關系在降維后得以保持，但是該算法沒有考慮原始數據的全局信息，從而可能出現降維后低維空間的整體結構特征與原始數據空間不一致，影響故障檢測的效果。為此，在LPP算法的基礎上，通過加入全局稀疏重構信息，提出了稀疏保局投影（sparse locality preserving projections，SLPP）降維算法。新算法在高維數據降維過程中不僅能夠保持原始數據的局部近鄰結構，而且能夠保持數據間的全局稀疏重構關系，更有利于提取過程數據的特征，SLPP的目標函數構建如式(7)所示。當i= j時，目標函數保證原樣本與其對應重構樣本在投影后的低維空間依然保持重構誤差最小；當xi與xj為k近鄰時，目標函數保證投影后的低維空間具有和原始數據空間相似的局部結構。

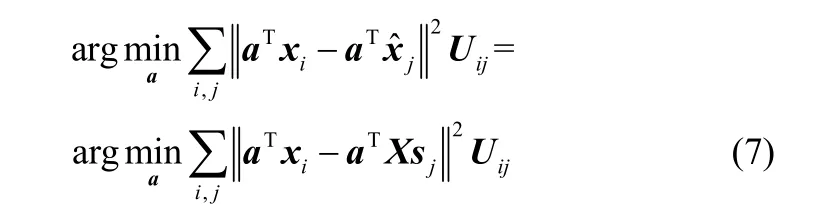
簡化式（7）所示目標函數

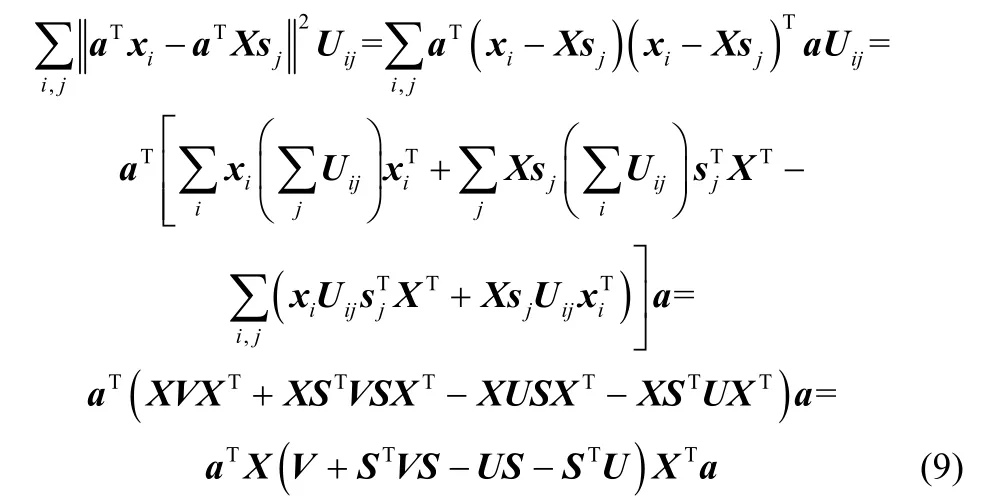
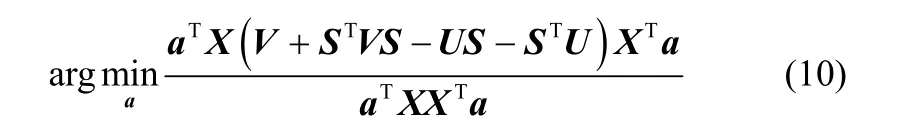
上述最優化問題的求解可以最終由以下廣義特征值問題求解

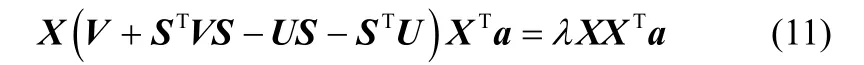
2.3 動態稀疏保局投影

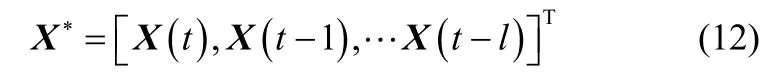
其中，l為滯后步長，根據經驗一般取l =1或2。可見，矩陣擴展后樣本數據減少到n l?，變量維數擴展為m( l + 1)。由于把過去時刻的變量測量值也作為當前時刻監控數據，考慮了不同時刻采樣點之間的關系，應用SLPP算法對上述增廣矩陣降維，便可以提取原始數據的動態特征，更有利于過程的故障檢測。是歸一化后的數據矩陣，考慮時序相關的特點將原始數據矩陣擴展為如下時滯增廣矩陣形式[16]

3 故障檢測算法

3.1 構造監控統計量

應用DSLPP算法進行數據降維后，分別對特征空間和殘差空間建立基于DSLPP的T2統計量和Q統計量[17]用于過程監控。將DSLPP算法求得的投影矩陣記為（其中m為變量數，d為低維空間維數），則有

其中，ynew是待檢測樣本xnew在特征空間的投影，Λ是正常工況數據特征空間的協方差矩陣。其中，為xnew的重構向量，

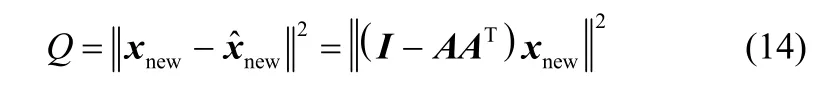
由于T2和Q統計量的分布未知，本文通過核密度估計[18]分別獲得兩監控統計量的控制限。

3.2 故障檢測算法實現

基于DSLPP算法的故障檢測過程包括離線建模和在線監控兩個階段，具體實現步驟描述如下。

離線建模階段：

與此同時，醫院創新性地將重要的無菌包的使用納入智能耗材柜的管理，無菌包的領取與醫囑相關聯，規范了無菌包的領取行為，實現無菌包使用的全程可追溯。

（1）采集過程正常運行數據并進行歸一化處理后，構造擴展矩陣，得到數據集?X；（2）使用DSLPP算法對數據集?X進行特征提取，得到投影矩陣A；

（3）分別計算特征空間的T2統計量和殘差空間的Q統計量的控制限。

在線監控階段：

（1）采集新的監控樣本數據并進行歸一化處理后，構造擴展矩陣，得到數據集；

（3）計算擴展樣本的T2統計量和Q統計量，并判斷是否超過相應控制限，若超過控制限，表明監控過程發生故障。

算法流程圖如圖1所示。

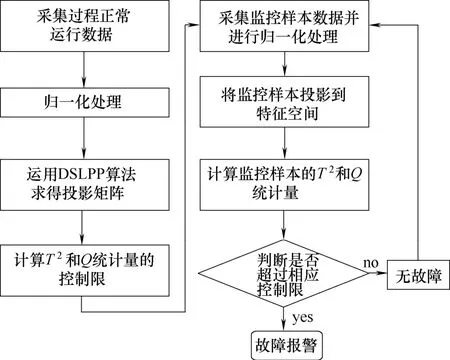
圖1 DSLPP算法流程圖Fig.1 Flow chart of DSLPP

4 仿真研究

田納西-伊斯曼過程（Tennessee Eastman process，TEP）[19]包含22個連續測量變量，19個組分測量變量和12個操縱變量，本文中的研究只選取其中的22個連續測量變量和11個操縱變量用于故障監控，由于組分測量變量在實際中很難測量，在這里不予考慮[20]。TEP有21種預設定的故障，這些故障中16個是已知的，5個是未知的。

采集正常工況下的960個數據作為訓練集，同樣采集960個故障工況下的數據作為測試集，故障于第161個樣本處加入。選取低維空間維數d =14，近鄰參數k =15，t =1，滯后步長l =1，所有置信限都設置為95%。為了降低誤報率，本文定義故障檢測時間為：第一次連續6個監控樣本超過統計量控制限的時間。故障漏報率指故障發生后未報警樣本與實際故障樣本數目的比值。本文以故障10和故障19為例，分別運用LPP、SLPP和DSLPP方法對其建立統計量監控模型，通過分析相應監控圖和仿真結果數據，比較3種方法的故障檢測性能。圖2和圖3分別為故障10和故障19的統計量監控圖，定量的故障檢測結果見表1。

表1 3種方法TEP故障檢測結果Table 1 Fault detection results of TEP with 3 methods

故障10是由流2的C進料溫度發生隨機變化引起的，圖2為故障10的統計量監控圖比較結果。結合表1的故障檢測結果可以發現，LPP的T2統計量在第210個樣本處發現故障，但是卻不能持續檢測故障，整個監控過程的漏報率很高；而SLPP的T2統計量在第182個樣本處發現故障，漏報率僅為10.25%；進一步考慮過程數據的動態性，DSLPP的T2統計量在第180個樣本處發現故障，漏報率降低為6.62%。另外，LPP、SLPP和DSLPP 3種方法的Q統計量分別在第195、185和176個樣本處檢測出故障，同樣表明了SLPP和DSLPP方法的優越性。以上結果表明了SLPP方法可以提取原始數據更全面的信息，有助于提高過程監控方法的故障檢測速度并降低其故障漏報率，而考慮過程數據動態性的DSLPP算法能進一步提高故障檢測性能。

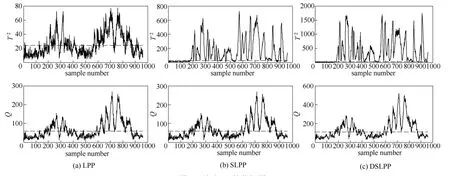
圖2 故障10的監控圖Fig.2 Monitoring charts of fault 10

圖3 故障19的監控圖Fig.3 Monitoring charts of fault 19

故障19是一種未知故障，圖3是其統計量監控圖。從T2統計量的結果來看，LPP在第343個樣本處檢測出故障，漏報率高達72.12%；SLPP的故障檢測效果要好很多，在第238個樣本處就檢測出故障，漏報率為51.12%；DSLPP效果最好，在第171個樣本處發現故障，漏報率進一步降低為41.62%。由此亦可以看出新算法檢測故障的有效性。

表1分別是3種故障檢測方法在一些典型故障發生時的故障檢測時間和故障漏報率。由表中數據可知，對于大多數故障情況，相比于LPP，SLPP無論在故障檢測時間方面還是故障漏報率方面都有著更出色的表現，而進一步考慮過程數據動態性的DSLPP更有助于提高過程監控方法的故障檢測速度并降低其故障漏報率。尤其對于故障10、16、19 和20，新方法可以大幅提高故障檢測性能。

5 結 論

本文在LPP算法的基礎上，通過加入全局稀疏重構信息，并進一步考慮過程數據的動態性，提出了一種基于動態稀疏保局投影的故障檢測方法。新方法在高維數據降維過程中不僅能夠保持原始數據的局部近鄰結構，而且能夠保持數據間的全局稀疏重構關系，更有利于對原始過程數據的特征提取，提高過程監控方法的性能。TEP的仿真結果表明，與LPP方法相比，新方法能更迅速檢測故障發生并降低過程監控漏報率。

References

[1] CHIANG L H, BRAATZ R D, RUSSELL E L. Fault Detection and Diagnosis in Industrial Systems [M]. Springer Science & Business Media, 2001.

[2] QIN S J. Survey on data-driven industrial process monitoring and diagnosis [J]. Annual Reviews in Control, 2012, 36 (2): 220-234.

[3] 王海清, 宋執環, 王慧. PCA 過程監測方法的故障檢測行為分析[J]. 化工學報, 2002, 53 (3): 297-301.

WANG H Q, SONG Z H, WANG H. Fault detection behavior analysis of PCA-based process monitoring approach [J]. Journal of Chemical Industry and Engineering (China), 2002, 53 (3): 297-301.

[4] LI G, QIN S J, ZHOU D. Geometric properties of partial least squares for process monitoring [J]. Automatica, 2010, 46 (1): 204-210.

[5] SCH?LKOPF B, SMOLA A, MüLLER K R. Nonlinear component analysis as a kernel eigenvalue problem [J]. Neural Computation, 1998, 10 (5): 1299-1319.

[6] TENENBAUM J B, SILVA V D, LANGFORD J C. A global geometric framework for nonlinear dimensionality reduction [J]. Science, 2000, 290 (5500): 2319-2323.

[7] ROWEIS S T, SAUL L K. Nonlinear dimensionality reduction by locally linear embedding [J]. Science, 2000, 290 (5500): 2323-2326.

[8] BELKIN M, NIYOGI P. Laplacian eigenmaps for dimensionality reduction and data representation [J]. Neural Computation, 2003, 15 (6): 1373-1396.

[9] HE X F, NIYOGI P. Locality preserving projections[C] //Proceedings of Advances in Neural Information Processing Systems. MIT Press, 2004: 153-160.

[10] HU K, YUAN J. Multivariate statistical process control based on multiway locality preserving projections [J]. Journal of Process Control, 2008, 18 (7): 797-807.

[11] ZHANG M G, GE Z Q, SONG Z H, et al. Global–local structure analysis model and its application for fault detection and identification [J]. Industrial & Engineering Chemistry Research, 2011, 50 (11): 6837-6848.

[12] AHARON M, ELAD M, BRUCKSTEIN A. K-SVD: an algorithm for designing overcomplete dictionaries for sparse representation [J]. IEEE Transactions on Signal Processing, 2006, 54 (11): 4311-4322.

[13] 馬小虎, 譚延琪. 基于鑒別稀疏保持嵌入的人臉識別算法 [J]. 自動化學報, 2014, 40 (1): 73-82.

MA X H, TAN Y Q. Face recognition based on discriminant sparsity preserving embedding [J]. Acta Automatica Sinica, 2014, 40 (1): 73-82.

[14] QIAO L, CHEN S, TAN X. Sparsity preserving projections with applications to face recognition [J]. Pattern Recognition, 2010, 43 (1): 331-341.

[15] WRIGHT J, YANG A Y, GANESH A, et al. Robust face recognition via sparse representation [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31 (2): 210-227.

[16] KU W, STORER R H, GEORGAKIS C. Disturbance detection and isolation by dynamic principal component analysis [J]. Chemometrics and Intelligent Laboratory Systems, 1995, 30 (1): 179-196.

[17] QIN S J. Statistical process monitoring: basics and beyond [J]. Journal of Chemometrics, 2003, 17 (8/9): 480-502.

[18] CHEN Q, WYNNE R J, GOULDING P, et al. The application of principal component analysis and kernel density estimation to enhance process monitoring [J]. Control Engineering Practice, 2000, 8 (5): 531-543.

[19] DOWNS J J, VOGEL E F. A plant-wide industrial process control problem [J]. Computers & Chemical Engineering, 1993, 17 (3): 245-255.

[20] LEE J M, QIN S J, LEE I B. Fault detection and diagnosis based on modified independent component analysis [J]. AIChE Journal, 2006, 52 (10): 3501-3514.

研究論文

Received date: 2015-11-26.

Foundation item: supported by the National Natural Science Foundation of China (61273160), and the Fundamental Research Funds for the Central Universities (14CX06132A).

Fault detection method based on dynamic sparse locality preserving projections

ZHENG Xin, TIAN Xuemin, ZHANG Hanyuan
(College of Information and Control Engineering, China University of Petroleum (East China), Qingdao 266580, Shandong, China)

Abstract:In order to deal with the problem that locality preserving projections (LPP) does not take into account the global structure and dynamic characteristic of process data, a new fault detection method based on dynamic sparse locality preserving projections (DSLPP) is proposed. In the study, the original data matrix is firstly extended to a time-delay augmented matrix. Then, a sparse coefficient matrix which can represent global sparse reconstructive relationship of data is gotten by solving an optimal problem of sparse representation (SR). The sparse coefficient matrix combines with the objective function of LPP to form a new objective function for dimensionality reduction. The new dimensionality reduction algorithm can not only preserve the local neighbor structure of the original data space, but also have better effect in preserving the global sparse reconstructive relationship. At last, DSLPP-based T2and Q statistics are constructed respectively in the feature space and residual space for fault detection．The simulation results of Tennessee Eastman process demonstrate that the proposed method detects faults more quickly and achieves lower fault missing alarm rate than the LPP method.

Key words:fault detection; locality preserving projections; sparse representation; feature extraction; process monitoring

DOI：10.11949/j.issn.0438-1157.20151769

中圖分類號：TP 277

文獻標志碼：A

文章編號：0438—1157（2016）03—0833—06

基金項目：國家自然科學基金項目（61273160）；中央高校基本科研業務費專項資金（14CX06132A）。

Corresponding author:Prof. TIAN Xuemin, tianxm@upc.edu.cn