基于狀態校正的積分對象預測控制算法及其應用

亓魯剛，李麗莉，欒志業，呂文祥，黃德先（清華大學自動化系，北京 00084；中華女子學院計算機系，北京 000）

?

基于狀態校正的積分對象預測控制算法及其應用

亓魯剛1，李麗莉2，欒志業1，呂文祥1，黃德先1
（1清華大學自動化系，北京 100084；2中華女子學院計算機系，北京 100101）

摘要：針對具有大滯后、強動態干擾的積分特性對象，提出了基于一階狀態校正的預測控制算法。算法考慮預測狀態與其對應的實際測量值偏差的積分作用，在一階維度上施加狀態校正，從而大幅提高控制器的預測準確性與應對模型失配的能力。通過仿真對比驗證了狀態校正算法的有效性。本算法已實際應用于某煉廠閃蒸罐的液位控制，取得了較好的控制效果。

關鍵詞：模型預測控制；過程控制；參數估值；積分對象；狀態校正

2015-11-26收到初稿，2015-12-11收到修改稿。

聯系人：黃德先。第一作者：亓魯剛（1986—），男，博士研究生。

引 言

預測控制具有魯棒性強、適應性廣等優點，在流程工業中得到廣泛應用[1-3]。相比于穩定對象的預測控制，積分過程因為具有非自衡性，控制難度相對較大。目前使用的主要預測控制算法主要考慮開環穩定過程的控制，對于開環不穩定過程需要先用PID控制，再以預測控制算法作為主回路控制[4-5]。針對不穩定對象，李嗣福[6]總結了采用預測控制算法控制一般表達式，提出了改進的模型算法控制控制無自平衡系統。欒志業等[7]提出了對對象模型分離的預測控制算法并應用于強非線性的間歇聚丙烯反應溫度控制。針對強干擾、準周期振蕩的具有積分特性的液位控制，Huang等[8]提出了變周期的控制策略，具有很強的魯棒性，在生產中得到了很好的應用。針對具有積分特性的工業對象，陳觀明等[9]通過建立參數模型與非參數模型相分離的預測模型，建立以此模型為基礎的預測控制算法，并通過計算機仿真實驗驗證了所提出方法的可行性。針對多步輸出預測算法只對當前的誤差進行反饋校正而無預測將來的誤差變化趨勢所造成誤差干擾的校正不夠及時、過渡過程時間偏長的問題，陳觀明[10]提出了一種具有誤差變化率預測校正的模型預測控制算法。針對基于輸入輸出模型的預測控制方法從原理上要求被控制對象具有開環穩定條件這一問題，基于狀態空間模型的預測控制方法應運而生[11-15]，也得到了進一步的發展和在實際應用中的成功應用[16-20]，但在應用時有需要狀態空間模型和所有狀態可測的限制。

針對具有大滯后、強動態干擾的積分特性對象，現有預測控制方法在實際應用中不能進行有效控制的難題，通過提取預測對象的一階特性，提出了一種基于一階狀態校正的預測控制算法，明顯提高了積分對象預測控制器的穩定性與魯棒性。對比仿真實驗與實際應用都充分展示了算法的良好控制效果。

1 積分特性對象與預測控制

針對具有積分特性的非最小相位系統是開環不穩定系統Guo(s)，系統結構可以看作開環穩定環節Gso(s)與積分環節的串聯：

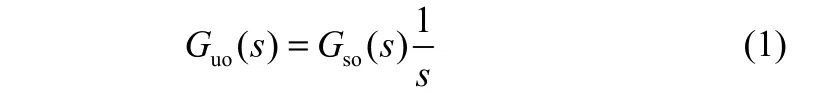
可用圖1來描述系統。

圖1 積分特性對象分解Fig.1 Integral system

圖中的u、x和y分別是輸入、狀態和輸出。

傳統的預測控制系統框圖，如圖2所示，主要由預測模型、反饋校正、滾動優化3部分組成。

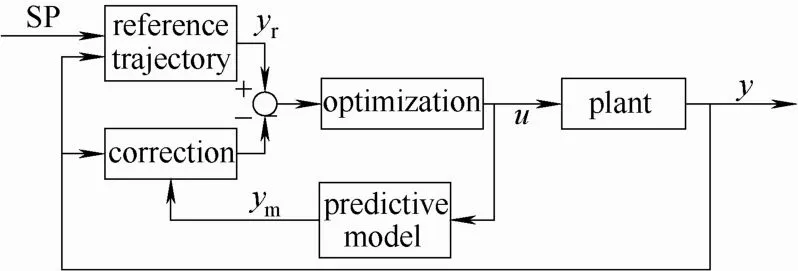
圖2 預測控制系統結構圖Fig.2 Predictive control system structure

為實現預測模型，文獻[9]將積分對象作相應的離散化處理，采樣時間為Ts，以穩態環節脈沖響應序列h1, h2, …, hN構造的積分系統離散化差分方程，用式(2)表示。

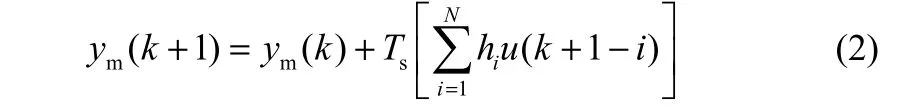
然后，依據傳統預測控制結構，得到控制律與預測向量，如式(3)、式(4)所示，式中的符號詳見文獻[9]。

積分對象的預測控制中，由于對象開環不穩定，對象Guo(s)可以看作是對應的穩定對象Gso(s)的積分，Gso(s)預測的微小偏差經過積分累積作用可以造成Guo(s)預測的顯著偏差。上述的預測控制方法在面對積分特性對象時，雖然取得一定的改進效果，但往往只有在模型失配不大時，不存在大的干擾情況下才能取得比較好的控制效果，在工程應用中復雜的工況變化使預測量不能準確表達實際狀態，遇到模型失配問題難以達到滿意的控制效果。

本文在文獻[9]所提預測控制方法的基礎上，從實際應用中總結發現面對積分特性對象，傳統的反饋校正，即零階校正，不能有效校正預測向量，因此通過提取被控變量的一階特性，再對預測向量實施一階校正，可以克服模型失配問題，完全有效控制積分特性對象。

2 預測校正

如前所述，面對積分特性對象，在傳統反饋校正的基礎上，考慮預測狀態的一階校正，為此引入兩個新變量，斜率Slop和旋轉因子（factor for rotate）fr。首先，采用最小二乘法在線滾動計算當前被控變量的斜率Slop，然后，旋轉由預測狀態與上一步預測狀態，使其逼近真實斜率，更大限度降低預測誤差。

二維空間上校正算法如圖3所示。

圖中描述了本文對預測序列的校正，分為平移校正（shift）與旋轉校正（rotate）兩部分。其中平移校正即為傳統反饋誤差校正，得到序列yp(k)；旋轉校正即本文提出的一階校正，得到序列ypc(k)。

一階狀態校正算法如下：

圖3 預測向量平移與旋轉校正Fig.3 Predictive vector of shift and rotate correction

ypc(k)與ypc(k－1)為旋轉校正后的預測狀態，作為下一時刻的預測初始向量，用于計算新的控制增量與預測向量。

經過上述校正后的校正控制器能比較精準地計算預測狀態，更為重要的是在一階維度上處理預測誤差，根本上降低積分特性對象下的預測誤差，能有效應對積分特性對象的模型失配問題。

3 仿真對比

利用Simulink搭建仿真環境，對比有無一階狀態校正控制器的控制效果。設被控系統模型為

為了對比模型失配情況下，有無校正的控制器的控制效果，以下面變化的對象模型為例仿真

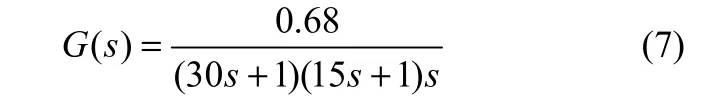
仿真環境如圖4所示。

圖4 積分特性對象仿真環境Fig.4 Simulation of integral system

仿真中，設置采樣時間為1 s，N=180，P=120，M=5，qi=3，λi=45，ri=0.9。另外，校正控制的速度因子fr=0.4。仿真總時長為2000 s。

仿真在100 s時，施加設定值階躍擾動，在1000 s時，施加控制增量擾動。然后，對比校正前后的控制曲線。

對于沒有模型失配時或模型失配較小時，有無校正的控制器都能獲得滿意的控制效果，只是未校正的控制器在穩定時也一直存在微小的振蕩。當模型失配逐漸加大到如式（6）所示，未校正控制器將出現如圖5所示的等幅振蕩，繼續加大將發散。相同仿真條件下，加校正的控制器都能獲得滿意的控制效果（圖6），并可以消除余差，展示了更強的穩定性與魯棒性，驗證了所提出的方法的有效性。

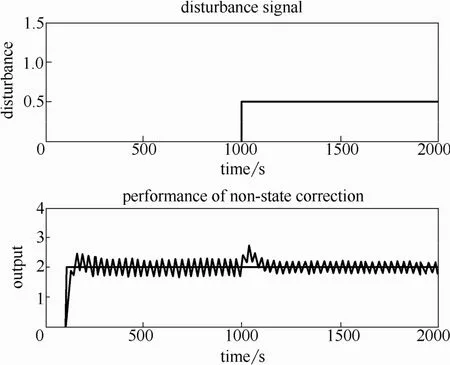
圖5 未校正控制器的控制效果Fig.5 Performance of non-state correction controller

圖6 校正控制器的控制效果Fig.6 Performance of state correction controller

4 應用實例

圖7 控制對象流程圖Fig.7 Field process

某煉廠常壓車間的閃蒸罐液位控制，閃蒸罐底部液位通過原油進料量控制。原油先后經過泵、脫前換熱器、三級電脫鹽罐、脫后換熱器、焦化爐對流室等環節進入閃蒸罐，流量約350 t·h?1。車間對閃蒸罐液位的要求在50%附近。控制對象的簡要流程如圖7所示。

圖8 現場應用中狀態校正控制器液位控制效果Fig.8 Performance of state correction predictive controller in field

本應用實例需要處理復雜的大滯后積分對象與多種干擾。從變頻泵的流量控制器至閃蒸罐液位之間經過多個對象，存在約4～5 min的純滯后；閃蒸罐液位儀表測量存在較大的噪聲；經過的電脫鹽罐油水界位調節帶入較大擾動等。應用實例中，原有常規控制無法控制大滯后積分對象，一直采用人工控制。針對該對象，開發了本文提出的校正控制器，投用后，展現了優異的控制性能，長期運行平穩。投用效果如圖8所示。

圖8展示了某日9～17時控制器投用前后液位控制效果對比。13時后，狀態校正控制器投用運行，控制液位在50%附近，有效降低液位波動幅度。長期運行統計顯示，液位超限時間減少90%，原油流量波動降低37%，大幅提高裝置生產運行的平穩率，同時提高裝置自控率，提高裝置控制效率，降低操作員勞動強度。

5 結 論

本文所提方法是從實際應用中挖掘出來的，面對積分特性對象，在已有預測控制方法基礎上，通過提取預測對象的一階特性，實施一階狀態校正，大幅度提高了積分對象預測控制器的穩定性與魯棒性。本文通過仿真對比驗證了所提出改進方法的有效性，并應用于某煉油廠閃蒸罐的液位控制，取得了好的控制效果。

References

[1] 黃德先, 王京春, 金以慧. 過程控制[M]. 北京: 清華大學出版社, 2011.

HUANG D X, WANG J C, JIN Y H. Process Control [M]. Beijing: Tsinghua University Press, 2011.

[2] QIN S J, BADGWELL T A. A survey of industrial model predictive control technology [J]. Control Engineering Practice, 2003, 11(7):733-764.

[3] 席裕庚, 李德偉, 林姝. 模型預測控制——現狀與挑戰[J]. 自動化學報, 2013, 39(3): 222-236.

XI Y G, LI D W, LIN S. Model predictive control — status and challenges [J]. Acta Automatica Sinica, 2013, 39(3): 222-236.

[4] 袁璞. 生產過程動態數學模型及其在線應用[M]. 北京: 中國石油出版社, 1994.

YUAN P. Dynamic Model of Chemical Process and Its Online Application [M]. Beijing: China Petrochemical Press, 1994.

[5] 席裕庚. 預測控制[M]. 北京: 國防工業出版社, 1993.

XI Y G. Predictive Control [M]. Beijing: National Defend Industry Press, 1993.

[6] 李嗣福. MAC和DMC的改進算法[J]. 自動化學報, 1993, 19(4): 413-419.

LI S F. Improvement algorithms of MAC and DMC [J]. Acta Automatica Sinica, 1993, 19(4): 413-419.

[7] 欒志業, 吳曉帆, 黃德先, 等. 基于模型分解的間歇聚丙烯過程預測控制[J]. 計算機與應用化學, 2006, 23(1): 20-24.

LUAN Z Y, WU X F, HUANG D X, et al. Model separating-based predictive control of batch polypropylene reaction process [J]. Computers and Applied Chemistry, 2006, 23(1):20-24.

[8] LYU W X, WANG Y H, HUANG D X, et al. Alterable period nonlinear level predictive control and its applications [C]// 3rd International Symposium on Advanced Control of Industrial Process. Jasper, Alberta, Canada, 2008.

[9] 陳觀明, 殷國富. 具有積分特性系統的預測控制算法[J]. 四川聯合大學學報(工程科學版), 1999, 3(3): 153-158.

CHEN G M, YIN G F. Predictive control algorithm for the system with integral character [J]. Journal of Sichuan Union University (Engineering Science edition), 1999, 3(3): 153-158.

[10] 陳觀明. 具有誤差變化率校正的預測控制算法[J]. 自動化與儀器儀表, 1999, (2): 7-9.

CHEN G M. Predictive control algorithm with error rate correction [J]. Automation and Instrumentation, 1999, (2): 7-9.

[11] 叢松波, 袁璞. 基于狀態方程的預估控制技術[C]//中國自動化學會第二屆過程控制科學報告會. 富陽, 浙江, 1988.

CONG S B, YUAN P. Predictive control technology based on stateequation [C]// Chinese Association of Automation 2nd Process Control Science Conference. Fuyang, Zhejiang, China, 1988.

[12] LI S F, LIM K Y, FISHER D G. A State-space formulation for model predictive control [J]. AIChE Journal, 1989, 35(2): 241-249.

[13] 袁璞, 左信, 鄭海濤. 狀態反饋預估控制[J]. 自動化學報, 1993, 19(5): 569-577. YUAN P, ZUO X, ZHENG H T. State variable feedback predictive control [J]. Acta Automatica Sinica, 1993, 19(5): 569-577

[14] MANFRED M, JAY H L. Model predictive control: past, present and future [J]. Computers and Chemical Engineering, 1999, (23): 667-682.

[15] 胡品慧, 袁璞. 狀態反饋預測控制系統的魯棒穩定性[J]. 控制與決策, 2001, 16(1): 126-128.

HU P H, YUAN P. Robustness of state feedback predictive control systems [J]. Control and Decision, 2001, 16(1): 126-128.

[16] ZHANG W Y, HUANG D X, WANG Y D, et al. Adaptive state feedback predictive control and expert control for a delayed coking furnace [J]. Chinese Journal of Chemical Engineering, 2008, 16(4): 590-598.

[17] TONG S W, LIU G P, WANG X G, et al. Real-time implementation of adaptive state feedback predictive control of PEM fuel cell flow systems using the singular pencil model method [J]. IEEE Transactions on Control Systems Technology, 2009, 17(3): 697-706.

[18] LI X G, HUANG D X, GAO D J. State feedback predictive control for hybrid system via parametric optimization [J]. Chinese Journal of Chemical Engineering, 2005, 13(5): 634-641.

[19] 李秀改, 高東杰. 混雜系統滾動時域狀態反饋預測控制研究與實現[J]. 自動化學報, 2004, 30(4): 567-571.

LI X G, GAO D J. Moving horizon state feedback predictive control for hybrid system based on mixed logic dynamic [J]. Acta Automatica Sinica, 2004, 30(4): 567-571.

[20] 黃德先, 田學民, 袁璞, 等. 預估控制策略在大純滯后過程的應用[J]. 化工自動化及儀表, 1995, 22(6): 10-14.

HUANG D X, TIAN X M, YUAN P, et al. The application of predictive control in large time-delay process [J]. Control and Instruments in Chemical Industry, 1995, 22(6): 10-14.

研究論文

Received date: 2015-11-26.

Foundation item: supported by the National Basic Research Program of China (2012CB720505) and the National Natural Science Foundation of China (21276137).

A predictive control algorithm of integral processes based on state correction and its application

QI Lugang1, LI Lili2, LUAN Zhiye1, Lü Wenxiang1, HUANG Dexian1
(1Department of Automation, Tsinghua University, Beijing 100084, China;2Department of Computer Science, China Women’s University, Beijing 100101, China)

Abstract:For integral processes with large lag, strong dynamic disturbance, the predictive control algorithm based on first-order state correction was proposed. Considering the integral effect of deviation between predictive and actual state, it exerts state correction on the first-order dimension. Thus the controller’s robustness is improved significantly. By simulation experiments, the effectiveness of the state correction algorithm was confirmed. And the algorithm has been adopted for liquid level control of flash tank in a refinery. The practical application results showed that the control effect is outstanding.

Key words:model-predictive control; process control; parameter estimation; integral process; state correction

DOI：10.11949/j.issn.0438-1157.20151763

中圖分類號：TQ 028.8

文獻標志碼：A

文章編號：0438—1157（2016）03—0685—05

基金項目：國家重點基礎研究發展計劃項目（2012CB720505）；國家自然科學基金項目（21276137）。

Corresponding author:Prof. HUANG Dexian, huangdx@tsinghua.edu.cn