基于遺傳算法的計算機水冷循環泵葉輪優化

呂玉坤, 肖卿宇

(華北電力大學 能源動力與機械工程學院，河北保定071003)

?

基于遺傳算法的計算機水冷循環泵葉輪優化

呂玉坤, 肖卿宇

(華北電力大學 能源動力與機械工程學院，河北保定071003)

摘要：在通過實算的方法設計計算機水冷循環泵葉輪的時候，需要手動多次調整葉輪的各種參數直到大體上水泵的各項性能能接近對應的設計要求的性能，所以需要大量重復的計算，并且得到的結果不一定是最好的。為了達到簡化設計過程并優化設計參數的目的，引入了水泵優化設計模型。首先，考慮到簡化多目標優化的復雜性，建立優化模型來使原本多目標優化問題轉化為單目標優化問題，使得僅用單一參數的大小便能衡量設計出的水泵滿足要求的程度。另外，考慮到設計參數的多樣性,采用了遺傳算法對該模型進行求解，得到在遺傳算法的迭代范圍內最優的設計參數。最后，通過算例來驗證這種方法，比較了實算法設計出來的結果和優化模型的方法設計出來的結果，發現了后者的水泵性能更能滿足設計要求，因此，達到了葉輪優化的目的。

關鍵詞：水泵葉輪；遺傳算法；優化

0引言

隨著計算機的運算速度逐漸加快，計算機CPU的過熱問題越來越嚴重，水冷散熱器以其工質的熱容量大，系統的熱負載能力強等優點而逐漸被采用。對于不同的散熱系統，需要不同的水冷循環泵來滿足工作狀態下揚程和流量的需求[1]。水泵的實際運行工況點，是由工作時的管路特性和水泵本身的特性共同決定的。因此，水泵能否運行于設計工作點附近對其運行的穩定性和經濟性有重要影響。實算方法需要大量迭代試算，直到滿足設計要求為止，設計所需的時間長[2]。而傳統的相似換算法[3，4]和速度系數設計法[5]也有很大的局限性。遺傳算法[6]的優越性在于能迅速找出一系列設計參數，使得設計的水泵最接近設計需求。因此，本文擬采用遺傳算法對循環泵葉輪設計過程進行優化，來探尋一個結合智能算法的設計途徑。

1水泵設計優化模型

為了消除量綱對優化過程的影響，采用以下方式處理參數：

(1)

式中：Kdi為第i個參數的設計值；Kmi為第i個參數的目標值；Ki為第i個參數處理之后的值。可見，若Ki等于1的時候，恰好滿足目標參數i的設計目標。

偏差量的表示方法有很多，這里用簡單的歐幾里得距離來表示各參數相對于目標值的偏差量。

(2)

式中：ei為參數i相對于目標值的偏差量。

由于每個設計參數都有一個小的優化目標，為了讓總體上的設計達到最優，這里確定如下目標函數:

(3)

式中：wi為第i個參數的目標權重∑wi=1；當wi越大時，參數i越重要，設計時便越先滿足參數i的目標。

2遺傳算法求解模型

遺傳算法是新一代的啟發式算法，具有很強的篩選能力，能避免傳統的拉格朗日算法陷入局部最優解情況，從而達到全局的優化目的。該算法通過模擬生物的進化過程，以目標函數作為依據，從而找到最能適應此函數的種群。其具體步驟如下。

2.1編碼

本次采用二進制編碼，設某一設計參數的取值范圍為(L,U)，使用長度為k的二進制編碼2表示其參數，則共有2k種不同的編碼。其對應關系如下：

所以：

(4)

2.2繁衍過程

(1)交配：用隨機數產生一個或多個交配點的位置，然后在交配點互換部分基因碼，形成兩個子個體。如父代S1=11110000，S2=01010101,如圖1,互換后四位基因，得到子代S1’=11110101,S2’=01010000。

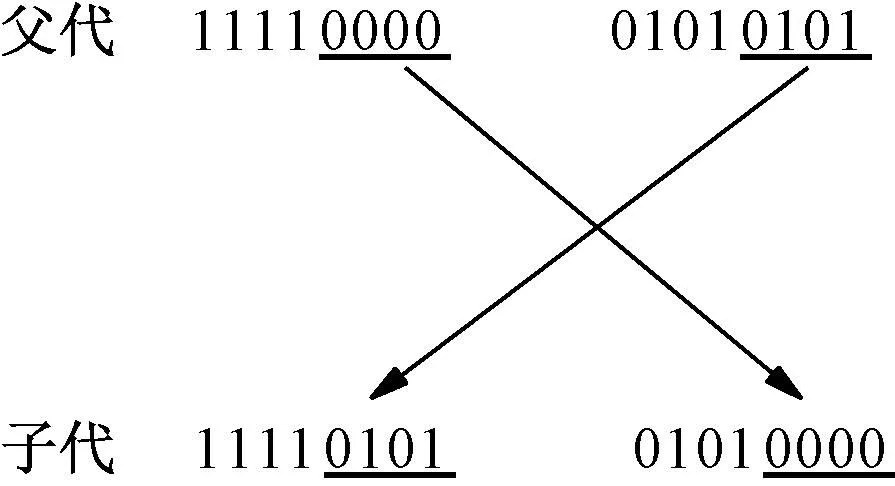
圖1　基因互換示意圖

(2)突變：基因碼的某位置有小概率進行翻轉，例如：S=11110000，第三位基因突變，得到：S’=11010000。

(3)適應度評估:適應度函數反應了個體對環境的適應能力，結合本次的設計內容來看，目標函數越小，適應度應該越高，可定義適應度函數為：

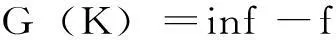
(5)

式中：inf為一個很大的數，可取100,即滿分100分。f是目標函數。分析可知，當設計參數恰好滿足目標的要求時，f為零，G達到最大，即最適應的基因。

3算例分析

3.1基本資料

某計算機CPU需要水冷散熱。通過傳熱計算得知，管路的流量為400 L/h時能滿足散熱要求，克服管路阻力所需的揚程為2 m。葉片進口直徑為0.0133 m，水泵出口直徑為0.006 m，電機的轉速不大于2 800 r/min。具體的設計要求見表1。

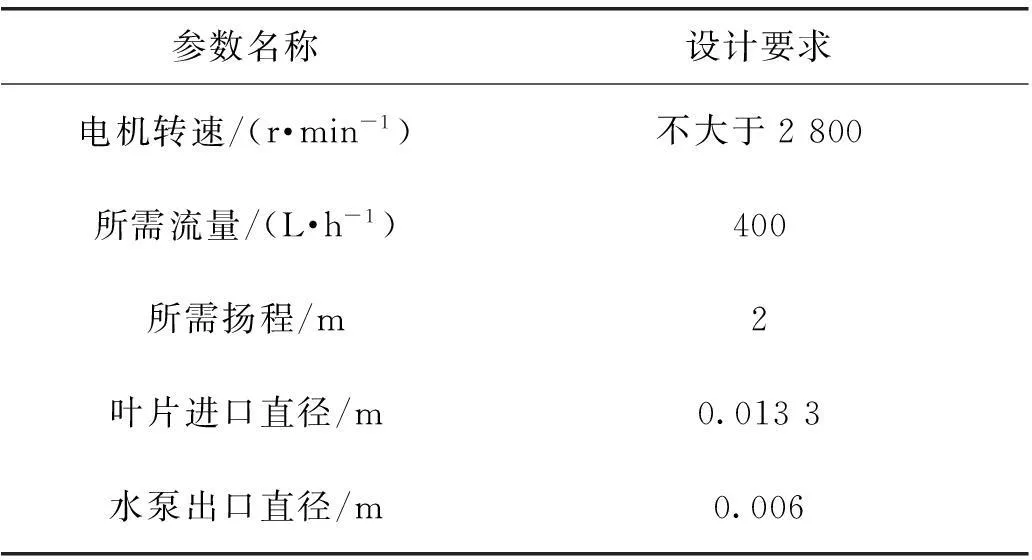
表1　基本設計要求

3.2實例求解

(1)基本參數設定

揚程裕量：

α=1.2

流量裕量：

β=1.2

所以設計揚程和流量為：

(6)

(7)

帶裕量的比轉速：

(8)

由(6)、(7)、(8)計算得：

Hd=2.4m

qvd=480L/h

ns=61.02

此為低比轉速離心泵D2d/D1≈3，葉輪為后向式并設水以徑向流入葉輪。其他設計參數見表2。

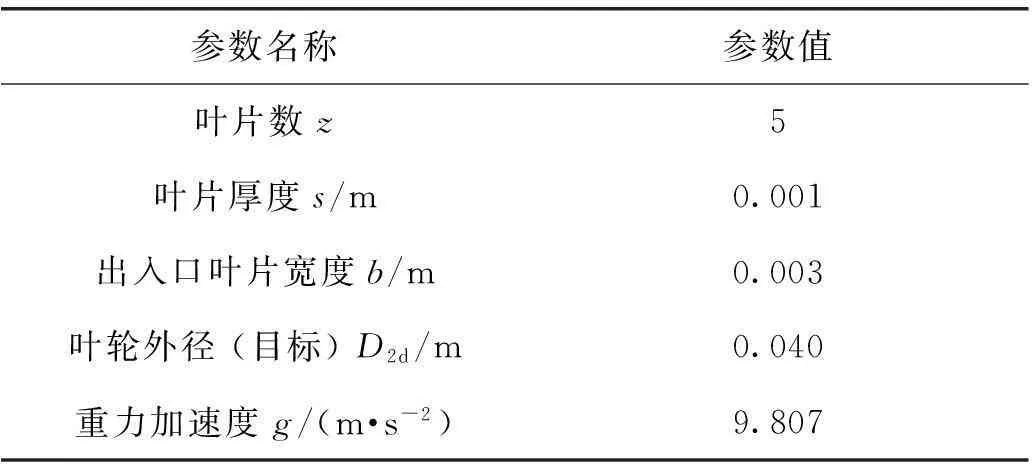
表2　其他參數的確定

(2)理論計算

水泵的部分效率可由經驗公式確定[7]:

機械效率:

(9)

容積效率：

(10)

流動效率：

(11)

斯托道拉滑移系數：

(12)

根據速度三角形(圖2和圖3)可以計算：

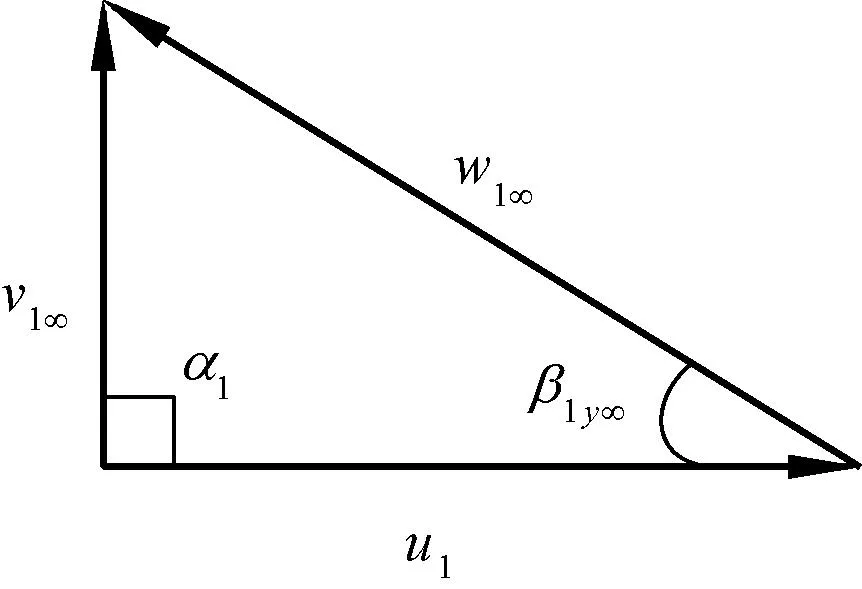
圖2　進口速度三角形

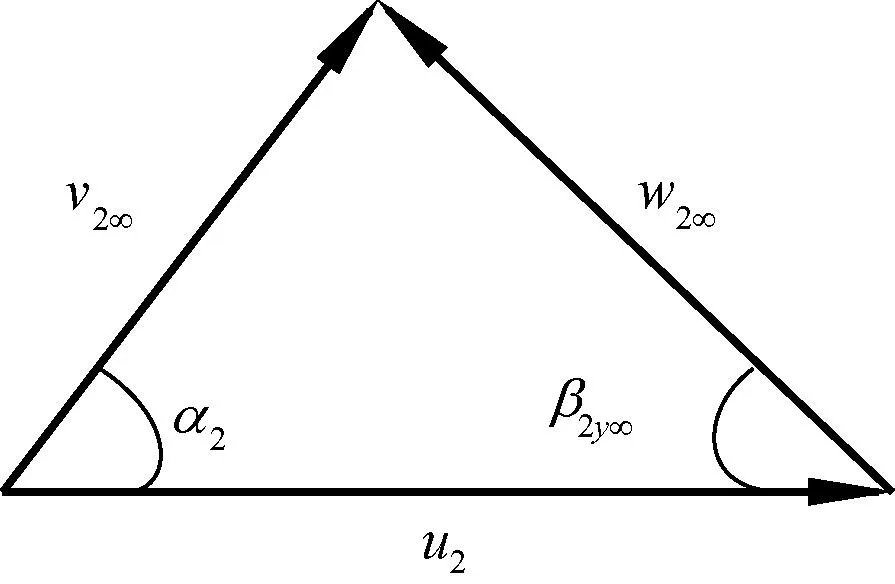
圖3　出口速度三角形

排擠系數：

(13)

設計總效率：

(14)

實際流量：

(15)

出口圓周速度：

u2=nπD2/60

(16)

出口徑向速：

(17)

出口絕對速度圓周分量：

(18)

進口徑向速度：

(19)

進口圓周速度：

u1=nπD1/60

(20)

葉片進口安裝角：

(21)

理論揚程：

(22)

葉片有時，限理論揚程：

(23)

揚程：

(24)

有效功率：

Pe=ρgqv

(25)

軸功率：

(26)

(3)流程圖及結果

優化的目標函數：

(27)

所需調整的參數[8，9]：電機轉速n、出口安裝角β2y以及葉輪外徑D2d。

調整參數的范圍：

0≤n≤2 800r/min

0≤D2d≤5D1

計算流程圖如圖4。

取種群數目為1 000，各個小目標的權重相等，得到求解結果：

f=0.019 3

G=99.980 7

n=2 800r/min

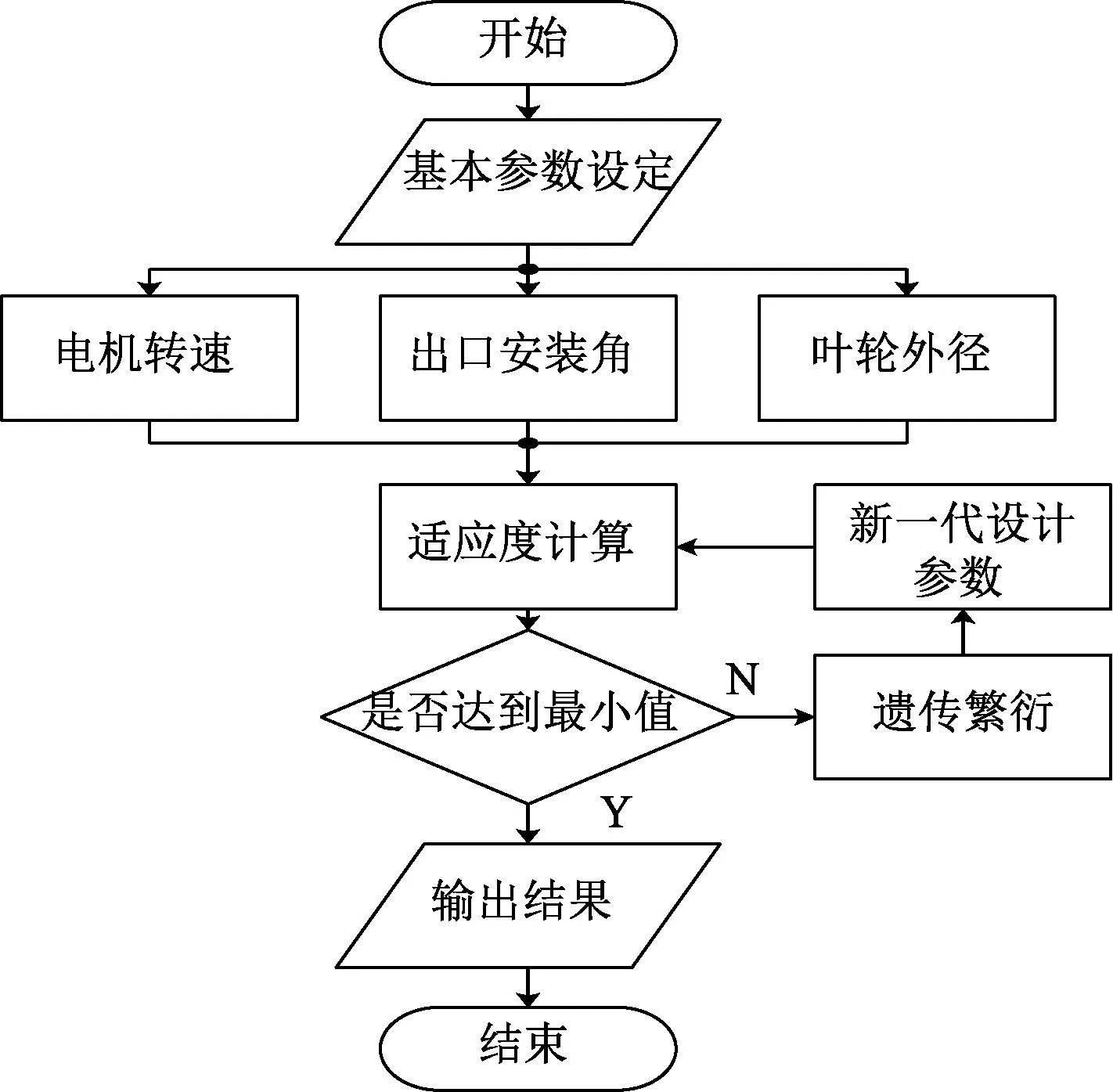
圖4　計算流程圖

D2d=0.045m

結果分析：

(1)目標函數f的值很小，可以認為基本滿足流量、揚程和外徑的規定目標。

(2)D2d/D1=3.375滿足文獻中[3]的D2d/D1≈3的規定。

(3)根據優化后的參數計算各個物理量，結果如表3所示，所有物理量都合理。

(4)實算方法得到的流量400 L/h和揚程1.93 m相比[2],本模型得到的流量459 L/h和揚程2.29 m(結果見表3)更接近設計要求的帶裕量流量480 L/h和揚程2.4 m。

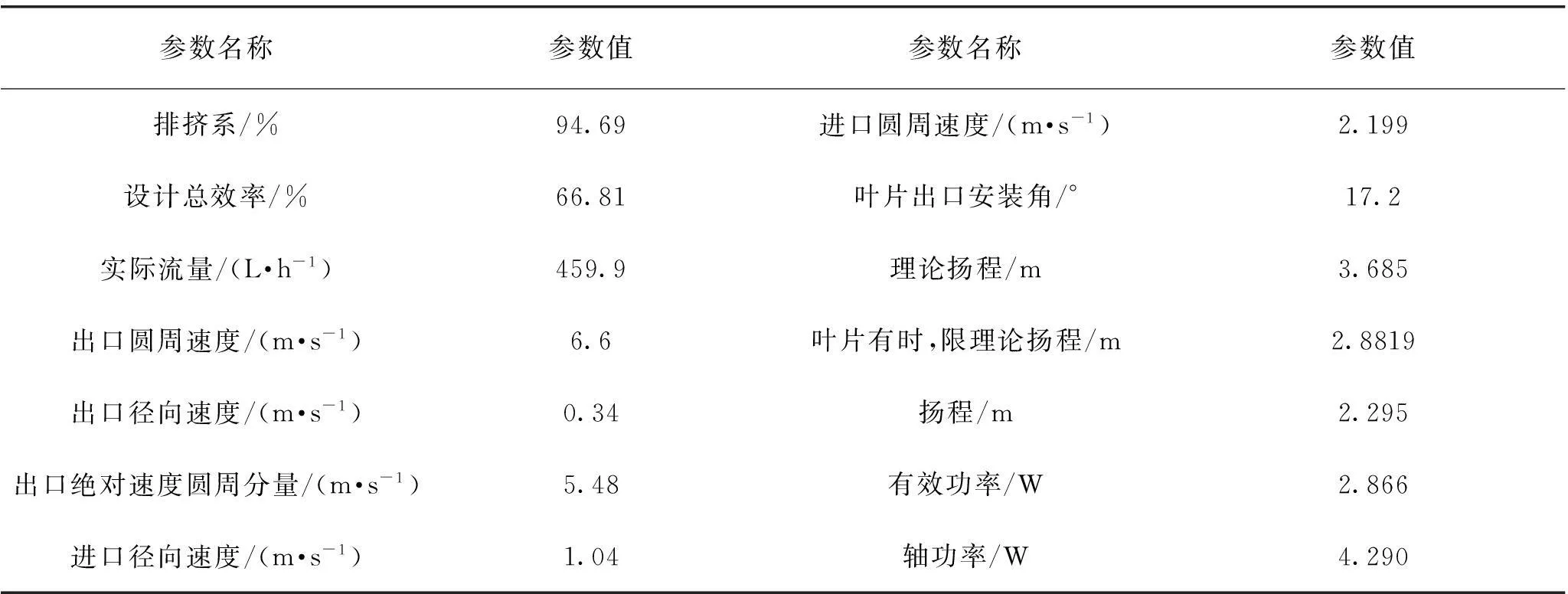
表3　各個物理量計算結果

4結論

通過比較水泵的性能結果，證明了本模型對水泵優化有很大的作用，大大提高了水泵的綜合性能，并且對于不同的優化目標，可以靈活修改優化目標的權值或增加減少目標項，甚至可以完全修改目標函數，以此來根據客戶的要求，針對性的完成不同的水泵設計任務。另外，本例中遺傳算法很好地完成了尋找最優葉輪參數的任務，對于更加復雜的設計任務，也可以用更加合適的算法進行尋優，從而設計出更加滿意的水泵葉輪。

參考文獻:

[1]朱海紅. 論葉輪設計對離水泵性能的影響[J]. 中國機械, 2014(15)： 22-23.

[2]呂玉坤, 徐國濤, 劉偉. 計算機水冷循環泵設計方法研究[J]. 華北電力大學學報(自然科學版), 2009, 36(2):44-47.

[3]安連鎖. 泵與風機[M]. 北京：中國電力出版社, 2001.

[4]高紅斌, 張汝琦, 孫楠,等. 相似定律在離心泵設計中的簡易應用[J]. 機械工程與自動化, 2010(5):74-75.

[5]葛宰林, 呂斌, 于馨. 基于速度系數法的離心泵葉輪優化設計[J]. 大連鐵道學院學報, 2006(3):37-40.

[6]卓金武. MATLAB在數學建模中的應用[M]. 北京：航空航天大學出版社, 2011.

[7]關醒凡. 現代泵理論與設計[M]. 北京：中國宇航出版社, 2011.

[8]KIM J H, OH K T, PYUN K B, et al. Design optimization of a centrifugal pump impeller and volute using computational fluid dynamics[C]// IOP Conference Series: Earth and Environmental Science. IOP Publishing, 2012:032025.

[9]何希杰，勞學蘇. 離心泵幾何參數灰色關聯度研究[J]. 水泵技術，2015(4)：16-19.

[10]戴正元, 李龍. 低比轉速離心泵設計理論現狀及發展[J]. 水泵技術, 2000(2):3-7.

Design Optimization of a Centrifugal Pump Impeller for CPU Refrigerating Using Genetic Algorithm

LV Yukun， XIAO Qingyu(School of Energy Power and Mechanical Engineering, North China Electric Power University, Baoding 071003, China)

Abstract：While designing a centrifugal pump impeller for CPU refrigerating, the parameters of the impeller should be dealt with manually to achieve the required performances of pump. Therefore, considerable repeated calculations are conducted to receive the satisfying results, which may not be the best ones. To streamline the designing process and optimize the parameters of the impeller, an optimization model of the pump is introduced. Firstly, considering of the complexity of multi-objective optimization(MOO), an optimization model is developed aiming at converting the problem of MOO to the problem of single-objective optimization(SOO), which can evaluate the degree of how well the pump will fit the requirements. Moreover, genetic algorithm(GA) is adopted to solve the model and obtains the best parameters by taking the diversity of the parameters into consideration . Finally, a study case is taken to verify the proposed method, and by comparing the calculated results with the ones that has already been studied, a series of better parameters are found by the proposed method. Thus, the goal of optimizationis achieved.

Keywords：pump impeller; genetic algorithm; optimization

中圖分類號:TM73

文獻標識碼:A

DOI:10.3969/j.issn.1672-0792.2016.03.013

作者簡介：呂玉坤 ( 1964- ), 男, 副教授, 主要從事泵與風機節能技術以及大型回轉機械經濟運行方面的研究，Email:luyukunf@126.com。

收稿日期：2015-12-14。