模的fann-內射維數及fann-平坦維數

徐龍玉,　萬吉湘,　喬　磊

(　　　1. 西南科技大學 理學院, 四川 綿陽 621010;　2. 綿陽師范學院 數學與計算機科學學院, 四川 綿陽 621000;

3. 四川師范大學 數學與軟件科學學院, 四川 成都 610066)

?

模的fann-內射維數及fann-平坦維數

徐龍玉1,萬吉湘2,喬磊3

(1. 西南科技大學 理學院, 四川 綿陽 621010;2. 綿陽師范學院 數學與計算機科學學院, 四川 綿陽 621000;

3. 四川師范大學 數學與軟件科學學院, 四川 成都 610066)

摘要：設R為環,給出R-模的fann-內射維數、fann-平坦維數概念,并在此基礎上定義R的左整體fann-維數(記為I.fa.ID(R))和R的右整體fann-平坦維數(記為r.fa.FD(R)).若記所有fann-內射R-模構成的類為FAI,證明了若FAI滿足單同態的上核是封閉的,則有I.fa.ID(R)=r.fa.FD(R),且此時I.fa.ID(R)≤1的充要條件是R的每個有限生成左零化子都是投射模.

關鍵詞：fann-內射模; fann-內射維數; fann-平坦模; fann-平坦維數; 左AC環

1預備知識

fann-內射模和fann-平坦模的概念最初見諸于文獻[1].對R的子集X,令

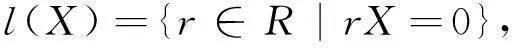
則l(X)稱為R的左零化子.注意有l(X)=l(I),其中I是由X生成的右理想.回顧右R-模N稱為fann-平坦模[1],是指對R的任意有限生成的左零化子l(I),自然同態N?Rl(I)→N?RR是單同態,亦即0→N?Rl(I)→N?RR是正合列.回顧左R-模M稱為fann-內射模[1],是指對環R的任意有限生成左零化子l(I),R-模同態f:l(I)→M都能擴張成同態g:R→M,即有交換圖1.

稱環R為左AC環,是指R的任意有限生成的左零化子理想l(I)都是有限表現的[1].顯然內射模是fann-內射模,平坦模是fann-平坦模.當R是整環時,任何模都是fann-內射模,也都是fann-平坦模.

(同調)維數一直是同調代數中研究的焦點.自然地,對任何由推廣內射模和推廣平坦模而得到的新的模類[2-12],人們總是希望定義新的維數來刻畫環的性質[13-17],其中,L. X. Mao等[13]給出了FP-投射維數的定義,并用此維數研究了Noether環和Coherent環,也得到了FP-內射維數與其他維數之間的關系.相應地,我們也利用fann-內射模和fann-平坦模定義模的fann-內射維數與模的fann-平坦維數,以及環的左整體fann-內射維數l.fa.ID(R)和右整體fann-平坦維數r.fa.FD(R).通過對這些維數的系統討論,給出AC環的許多性質刻畫.

本文中所有的環都是帶有單位元1的結合環,所有的模都是酉模.

2fann-內射維數及fann-平坦維數

定義 2.11) 設M是左R-模,M的左fann-內射維數是指使得Extn+1(R/l(I),M)=0的最小非負整數n,記為l.fa-id(M)=n,其中l(I)取遍環R所有有限生成的左零化子理想.如果這樣的n不存在,則稱M的左fann-內射維數為∞,記為l.fa-id(M)=∞.

2) 定義

l.fa.ID(R)=sup{l.fa-id(M)|M∈RM},

稱之為環R的左整體fann-內射維數.

定義 2.21) 設N是右R-模.N的右fann-平坦維數是指使得Torn+1(N,R/l(I))=0的最小非負整數n,記為r.fa-fdRN=n,其中l(I)取遍環R所有有限生成的左零化子理想.如果這樣的n不存在,則稱N的右fann-平坦維數為∞,記為r.fa-fd(N)=∞.

2) 定義

r.fa.FD(R)=sup{r.fa-fd(N)|N∈MR},

稱之為環R的右整體fann-平坦維數.

例 2.3自然地,左R-模M是fann-內射模當且僅當l.fa-id(M)=0.同理,右R-模N是fann-平坦模當且僅當r.fa-fd(N)=0.對任何右(或左)R-模N,記N+=HomZ(N,Q/Z),稱之為N的特征模.

命題 2.4右R-模N是fann-平坦右R-模當且僅當N+是fann-內射左R-模.

證明對R的任意有限生成的左零化子理想l(I),由自然同構

知結論成立.

命題 2.5設{Mi}是一簇左R-模,則⊕Mi是fann-內射模當且僅當每一Mi是fann-內射模.

證明對環R的任意有限生成的左零化子理想l(I),由自然同構

知結論成立.

下面把fann-內射左R-模類和fann-平坦右R-模類分別記為FAI和FAF.

命題 2.6模類FAF在純子模下封閉.

證明設A是fann-平坦右R-模B的純子模.由文獻[18],0→(B/A)+→B+→A+→0是分裂的正合列.由命題2.4,B+是fann-內射左R-模,因此有A+是fann-內射左R-模.仍由命題2.4,A是fann-平坦模.

定理 2.7對環R,以下條件等價:

1) 環R是左AC環;

2) fann-平坦右R-模的直積是fann-平坦模;

3) 左R-模M是fann-內射模當且僅當M+是fann-平坦右R-模.

定理 2.8對環R,以下等價:

1) l.fa.ID(R)=0;

2) r.fa.FD(R)=0;

3) 每個左R-模是fann-內射模;

4) 每個右R-模是fann-平坦模;

5) 每個有限生成的左零化子理想l(I)是R的純子模.

定理 2.9對環R,以下條件等價:

1) FAI中單同態的上核是封閉的;

2)R是左AC環,且FAF中滿同態的核是封閉;

3)R是左AC環,且有Tork(N,R/l(I))=0,其中k≥1,N是fann-平坦右R-模,l(I)是R的有限生成左零化子;

4) Extk(R/l(I),M)=0,其中k≥1,M是fann-內射左R-模,l(I)是R的有限生成的左零化子.

其次令0→A→B→L→0是右R-模正合列,其中B及L是fann-平坦右R-模,則有正合列0→L+→B+→A+→0,又因為B+及L+是fann-內射左R-模,故A+是fann-內射左R-模,則A是fann-平坦右R-模.

為陳述簡潔起見,我們用(X)表示性質:模類FAI滿足單同態的上核是封閉的.

顯然無零因子環有性質(X).

定理 2.10設環R有性質(X),則對左R-模M,以下條件等價:

1) l.fa-id(M)≤n;

2) 設0→M→E0→E1→…→En-1→Ln→0是正合列,其中E0,E1,…,En-1是fann-內射模,則Ln是fann-內射R-模;

3) 對R的每個有限生成的左零化子l(I),有Extn+1(R/l(I),M)=0;

4) 對R的每個有限生成的左零化子l(I),及k≥1,有Extn+k(R/l(I),M)=0.

對偶地,可以證明下面的定理.

定理 2.11設環R有性質(X),則對右R-模N,以下條件等價:

1) r.fa-fd(N)≤n;

2) 設0→Kn→Fn-1→…→F1→F0→N→0是正合列,其中F0,F1,…,Fn-1是fann-平坦右R-模,則Kn是fann-平坦右R-模;

3) 對R的每個有限生成的左零化子l(I),有Torn+1(N,R/l(I))=0;

4) 對R的每個有限生成的左零化子l(I),及任何k≥1,有Torn+k(N,R/l(I))=0.

定理 2.12設環R有性質(X),n是非負整數,則l.fa.ID(R)≤n當且僅當r.fa.FD(R)≤n.

推論 2.13設環R有性質(X),則l.fa.ID(R)=r.fa.FD(R).

定理 2.14設R有性質(X),且l.fa.ID(R)<∞,則l.fa.ID(R)=r.fa.FD(R)=l.fa-id(RR).

證明只需證l.fa.ID(R)≤l.fa-id(RR).設m=l.fa-id(RR)<∞,則有正合列0→R→E0→E1→…→Em-1→Em→0,其中E0,E1,…,Em-1,Em是fann-內射模.于是有正合列0→⊕R→⊕E0→⊕E1→…→⊕Em-1→⊕Em→0,于是對任意自由左R-模F有l.fa-id(F)≤m.

記n=l.fa.ID(R)<∞.設M是左R-模,取正合列0→Kn→Fn-1→…→F1→F0→M→0,其中F0,F1,…,Fn-1是自由模.由于l.fa-id(Kn)≤n,及l.fa-id(Fi)≤m,則對R的有限生成的左零化子l(I),有Extm+1(R/l(I),M)?Extm+n+1(R/l(I),Kn)=0,故l.fa-id(M)≤m,因此有n≤m.

定理 2.15對環R,以下條件等價:

1)R的有限生成的左零化子l(I)是投射模;

2)R是左AC環,且fann-平坦右R-模的子模是fann-平坦模;

3)R是左AC環,且R的右理想是fann-平坦模;

4) fann-內射左R-模的商模是fann-內射模;

當R有性質(X)時,上面各條又等價于:

5) l.fa.ID(R)≤1;

6) r.fa.FD(R)≤1.

參考文獻

[1] 徐龍玉,汪明義. 關于零化子凝聚環[J]. 四川師范大學學報(自然科學版),2006,29(2):161-165.

[2] 王芳貴,汪明義,楊立英. 交換環上的極大性內射模[J]. 四川師范大學學報(自然科學版),2010,33(1):1-9.

[3] 章聚樂,陳建龍.P-內射環和半素環[J]. 數學雜志,1991,11(1):29-34.

[4] 趙玉娥,杜先能. 關于廣義內射模的一些研究[J]. 四川師范大學學報(自然科學版),2008,31(5):16-18.

[5] 易忠. 關于quasi-投射模和quasi-內射模[J]. 廣西師范大學學報(自然科學版),1985,3(1):18-26.

[6] 余柏林. π-凝聚環的推廣[J]. 四川師范大學學報(自然科學版),2005,28(3):278-281.

[7] 李珊珊,汪明義. 關于p-平坦模[J]. 廣西師范大學學報(自然科學版),2004,22(1):36-40.

[8] GUPTA R N. Onf-injective modules and semihereditary rings[J]. Proc Nat Inst Sci,1969,35(1):323-328.

[9] JAIN S. Flat and FP-injectivity[J]. Proc Am Math Soc,1973,41(2):437-442.

[10] 徐龍玉,宋暉. 關于fann-內射模[J]. 四川師范大學學報(自然科學版),2009,32(4):443-446.

[11] 陳文靜,楊曉燕. 弱Gorenstein FP-內射模[J]. 四川師范大學學報(自然科學版),2014,37(4):477-481.

[12] 尹華玉,陳幼華. π-整環上形式冪級數的容度準則[J]. 四川師范大學學報(自然科學版),2014,37(4):451-454.

[13] MAO L X, DING N Q. FP-projective dimensions[J]. Commun Algebra,2005,33:1153-1170.

[14] STENSTROM B. Coherent rings and FP-injective modules[J]. J London Math Soc,1972,2:372-383.

[15] NG H K. Finitely presented dimension of communicative rings and modules[J]. Pacific J Math,1984,113(2):25-40.

[16] 汪明義. 代數學中Frobenius的結構[M]. 北京:科學出版社,2005:78-96.

[17] 王芳貴. 交換環與星型算子理論[M]. 北京:科學出版社,2006:142-193.

[18] ENOCHS E. A note on absolutely pure modules[J]. Canad Math Bull,1976,19(3):361-362.

2010 MSC：13C10; 13C11; 13D07

(編輯鄭月蓉)

On Fann-Injective Dimension and Fann-Flat Dimension

XU Longyu1,WAN Jixiang2,QIAO Lei3

(1.CollegeofScience,SouthwestUniversityofScienceandTechnology,Mianyang621010,Sichuan;2.CollegeofMathematicsandComputerScience,MianyangNormalCollege,Mianyang621010,Sichuan;3.CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan)

Abstract：In this paper, for a ring R the notions of fann-injective dimension and fann-flat dimesion are introduced. Based on these, the left global fann dimension of R, denoted by I.fa.ID(R) and the right global fann dimension of, denoted by r.fa.FD(R) are defined. Moreover, let (X) express the codition that the uppe kernelsof injective homomorphisms are closed and denote the class of all fann-injective R-modules as FAI. It is proved that if FAI satisfies (X) then I.fa.ID(R)=r.fa.FD(R) and in this case, I.fa.ID(R)≤1 if and only if every finitely generated left annihilator in R is projective.

Key words：fann-injective modules; fann-injective dimension; fann-flat modules; fann-flat dimension; left AC ring

doi:10.3969/j.issn.1001-8395.2016.01.006

中圖分類號：O153; O154

文獻標志碼：A

文章編號：1001-8395(2016)01-0033-04

作者簡介：徐龍玉(1979—),女,講師,主要從事環與模范疇理論的研究,E-mail:xulongyu3@163.com

基金項目：國家自然科學基金(11171240)

收稿日期:2014-07-08