“函數的單調性”復習設想

?

“函數的單調性”復習設想

◇江蘇周愛飛

函數是高中數學重要章節,函數的單調性是其中的一個重要的概念,也是高考的熱點問題.復習時要通過例題的設置引導學生充分理解、靈活運用概念,培養學生對單調性問題的轉換能力．本文就“函數單調性”的考點復習進行分類突破,望能有助于高考復習實踐．

1暴露學生常見錯誤

【設計意圖】 將例1拿出來讓學生自主探究,可以暴露出學生認知上最為常見的錯誤.

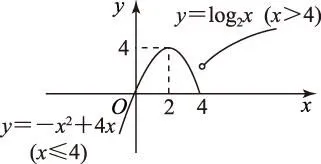
有學生會認為f(x)在(-∞,0)∪(0,+∞)上是單調減函數,實際上只要取x1=-1,x2=1,其中x1

2內化解決問題的方法

【設計意圖】本例的解決方法可以運用定義法(略),也可以用復合函數法,相比較而言用后者方法更簡單．

復合函數法設x2-2x-3=t,則y=log1/2t且t>0,所以x>3或x<-1．又t=(x-1)2-4,y=log1/2t關于t>0為減函數,求原來的函數單調遞減區間,即求函數t=x2-2x-3>0的遞增區間,所以原函數的單調遞減區間為(3,+∞).

【設計意圖】本例的解題方法可以運用定義法(略),也可以用導數法,相比較而言用后者更簡單．

【設計意圖】本例引導學生運用圖象法,同時讓學生有一種意識:有些函數較易畫出草圖,可用函數圖象法輔助求解.

圖象法作出函數f(x)的圖象如圖1所示:

圖1

由圖象可知f(x)在(a,a+1)上單調遞增,需滿足a≥4或a+1≤2,即a≤1或a≥4．

(作者單位：江蘇省江陰市華姿中等專業學校)