基于TOPSIS&Shapley值法的物流聯(lián)盟利益分配研究

林　翊　王現(xiàn)兵

（福建師范大學，福建　福州　350117）

?

基于TOPSIS&Shapley值法的物流聯(lián)盟利益分配研究

林翊王現(xiàn)兵

（福建師范大學，福建福州350117）

摘要：物流市場日益激烈的競爭促使物流企業(yè)傾向于采取聯(lián)盟運營模式，而合理利益分配是物流聯(lián)盟保持穩(wěn)定的關(guān)鍵。在已有關(guān)于物流聯(lián)盟研究的基礎上，以物流企業(yè)的邊際貢獻度、風險、投資額、任務、服務能力為權(quán)重因子，采用TOPSIS法和Shapley值法結(jié)合方法為物流聯(lián)盟構(gòu)建優(yōu)化的利益分配模型。并通過算例分析驗證利益分配的合理性，以期為利益分配模型在物流聯(lián)盟利益分配的運用及相關(guān)研究提供參考。

關(guān)鍵詞：物流聯(lián)盟；利益分配；TOPSIS法；Shapley值法

一、文獻綜述

物流企業(yè)為應對市場競爭及獲取可持續(xù)經(jīng)營，選擇物流聯(lián)盟運營模式較為普遍。物流聯(lián)盟是企業(yè)之間以物流服務為合作基礎的戰(zhàn)略聯(lián)盟，借助物流聯(lián)盟，物流企業(yè)能夠在交易費用、協(xié)同效應等角度獲取競爭優(yōu)勢[1]。然而，物流聯(lián)盟與其他類型聯(lián)盟一樣，也面臨不穩(wěn)定性威脅。Lunnan、Haugland以資源基礎理論為研究背景，指出約有30％～70％的戰(zhàn)略聯(lián)盟會提前解體[2]。另外，也有學者指出物流企業(yè)形成物流聯(lián)盟體的直接動力是獲取更多經(jīng)濟利益[3]。因此，合理選取影響物流聯(lián)盟穩(wěn)定的利益分配因素，并據(jù)此選用恰當利益分配方法為物流聯(lián)盟搭建公平、合理的利益分配模型具有重要意義。

當前，已有學者從多角度研究物流聯(lián)盟的影響因素以及利益分配。其中，在聯(lián)盟穩(wěn)定性研究上，魏瑋運用博弈論框架分析戰(zhàn)略聯(lián)盟組織不穩(wěn)定原因，揭示了戰(zhàn)略聯(lián)盟穩(wěn)定的關(guān)鍵在于組織內(nèi)成員的博弈支付結(jié)構(gòu)和博弈者對未來的預期[4]。杜義飛、李仕明、陳德富等認為參與者對價值創(chuàng)造的貢獻直接影響聯(lián)盟的穩(wěn)定性，且價值創(chuàng)造的特征函數(shù)結(jié)構(gòu)同聯(lián)盟創(chuàng)造的最小價值之間存在線性變換關(guān)系[5]。徐揚、申金升、王傳濤從經(jīng)濟學和系統(tǒng)學角度對物流企業(yè)風險厭惡程度、聯(lián)盟協(xié)同效應以及各種成本系數(shù)等物流聯(lián)盟穩(wěn)定性影響因素進行分析，指出獨立經(jīng)營成本系數(shù)和合作成本系數(shù)對物流企業(yè)的聯(lián)盟[6]。江琳琳采用BP神經(jīng)網(wǎng)絡方法對物流聯(lián)盟中存在的風險進行研究，指出物流聯(lián)盟存在關(guān)系風險和績效風險，并進一步細分11個二級風險指標[7]。

在物流聯(lián)盟利益分配研究上，靳慧斌、劉明廣介紹基于全因素評價的利潤分配機制，并指出全因素包括企業(yè)特質(zhì)、實際貢獻、努力程度、承擔風險以及動態(tài)運營等[8]。馬小龍?zhí)岢鰟討B(tài)物流聯(lián)盟利益分配應遵循多勞多得、風險補償、效用最大化和綜合優(yōu)化等四項原則[9]。甘家華、王建偉、陳卓等構(gòu)建混合模式下的中小物流企業(yè)聯(lián)盟收益分配模型，并認為聯(lián)盟收益分配受可分配收益、承擔物流任務數(shù)量、任務完成質(zhì)量、投資額、聯(lián)盟損失等幾大主要因素影響[10]。在具體的聯(lián)盟利益分配方法上，易欣、張飛漣、邱慧等指出，Shapley值法下的聯(lián)盟利益分配不僅體現(xiàn)了每個聯(lián)盟成員對該聯(lián)盟的平均貢獻，而且反映出個人在集體中的重要性，分配原理和分配結(jié)果容易被各個聯(lián)盟成員視為公平[11]；而Shapley主要依據(jù)聯(lián)盟成員的邊際貢獻為依據(jù)進行分配，隨著聯(lián)盟合作的深化，成員之間的聯(lián)盟地位差距逐步縮小，物流成員為聯(lián)盟運營所做出的其他努力因素對利益分配的影響日益增大。因此，李靚、劉征馳、周堂從投資額、風險承擔等角度對基于貢獻度的Shapley值法利益分配模型進行了修正，以此搭建基于風險和貢獻度的聯(lián)盟利益分配模型[12]。也有研究應用TOPSIS法對綜合利益分配進行了分析，例如楊晶、江可申、邸強在聯(lián)盟利益的綜合分配研究中，利用TOPSIS為基于負理想點、基于正理想點、Shapley值法等所構(gòu)建的利益分配方案賦予權(quán)重，以確定綜合因素下的協(xié)調(diào)性聯(lián)盟利益分配模型[13]；顧桂蘭在協(xié)同利益分配的研究中，為避免利益分配的單因素性，利用TOPSIS法對基于投入、貢獻、風險的三種利益分配賦予合理權(quán)重，構(gòu)建體現(xiàn)協(xié)調(diào)性的利益分配模型，并通過算例驗證了利益分配模型的合理性[14]。

綜上所述，研究擬運用Shapley值法依據(jù)聯(lián)盟成員邊際貢獻度為物流聯(lián)盟構(gòu)建體現(xiàn)邊際貢獻的利益分配模型。另外，為兼顧物流企業(yè)為構(gòu)建聯(lián)盟所承擔風險、投資額、任務量等相關(guān)努力因素，在分析物流聯(lián)盟利益分配具體影響因素基礎上，研究運用具備運算簡單、結(jié)果合理等特征的TOPSIS定權(quán)函數(shù)法對除邊際貢獻度外的其他相關(guān)利益分配影響指標進行歸納，以確定物流聯(lián)盟成員的利益分配權(quán)重。并通過將兩種利益分配模型進行結(jié)合，為物流聯(lián)盟構(gòu)建體現(xiàn)綜合評價的利益分配。

二、物流聯(lián)盟利益分配影響因素分析

物流企業(yè)參與構(gòu)建物流聯(lián)盟主要以應對市場競爭、獲取可持續(xù)經(jīng)營，即為獲取比獨立經(jīng)營多的利益為目的，利益分配模型對物流聯(lián)盟穩(wěn)定性具有重要影響。為合理確定物流聯(lián)盟的利益分配權(quán)重指標，根據(jù)物流企業(yè)自身經(jīng)營特征，將物流聯(lián)盟利益分配影響因素歸類為邊際貢獻度、投資額、承擔風險、任務承擔、物流服務能力五個方面。其中，邊際貢獻度主要與物流企業(yè)的營業(yè)收入、市場占有率等經(jīng)營業(yè)績相關(guān)，也是物流聯(lián)盟利益分配的主要影響因素之一。因此本文主要對投資額、承擔風險、任務承擔、物流服務能力四項指標體系進行分析。

（一）投資額

物流企業(yè)是以提供運輸、配送、倉儲、流通加工等服務的企業(yè)，以資源密集型服務為特征。因此，物流企業(yè)聯(lián)合構(gòu)建物流聯(lián)盟的投資主要以有形資產(chǎn)投入為主，無形資產(chǎn)投入為輔。其中，有形資產(chǎn)投入包括倉庫、車輛、建筑、設備等固定資產(chǎn)以及投入融資資金、人力資源等相關(guān)要素；無形資產(chǎn)則包括客戶關(guān)系、市場競爭力、企業(yè)知名度等相關(guān)隱性資產(chǎn)。在物流聯(lián)盟的利益分配中，成員投資額是重要的決定因素之一。

（二）承擔風險

風險是物流聯(lián)盟利益分配的重要影響因素，也是物流聯(lián)盟利益分配的重要影響因素。根據(jù)風險來源，將物流聯(lián)盟成員承擔的風險種類分為內(nèi)部風險和外部風險。其中，內(nèi)部風險是來自物流聯(lián)盟內(nèi)部的各種威脅，一般包括物流協(xié)同服務形成的物流作業(yè)風險、信息傳遞風險、物流協(xié)調(diào)風險、個體利益誘因下的搭便車行為風險、控制與反控制風險等。外部風險是物流聯(lián)盟以及物流成員經(jīng)營所面對的外部沖擊，主要包括政治、經(jīng)濟、技術(shù)、社會等方面。在對聯(lián)盟成員承擔風險的評價過程中，既要考慮成員承擔的物流聯(lián)盟風險，也要考慮物流企業(yè)在參與聯(lián)盟體前后的風險承擔能力以及風險變化。

（三）任務承擔

物流企業(yè)組建聯(lián)盟的本質(zhì)是通過協(xié)同物流服務實現(xiàn)盈利，任務承擔量是聯(lián)盟利益分配的重要依據(jù)。根據(jù)資源基礎理論，由于物流成員服務能力的差異，才有構(gòu)建物流聯(lián)盟體的必要性。因此，在聯(lián)盟體制下，物流企業(yè)成員承擔的任務性質(zhì)以及數(shù)量有所不同，物流聯(lián)盟的利益分配要體現(xiàn)任務承擔因素的影響。在評價物流企業(yè)任務承擔量過程中，不僅要考慮物流企業(yè)的任務承擔量，同時要綜合考慮承擔任務類別，以公平、科學地確定任務承擔權(quán)重因子。

（四）物流服務能力

提高物流服務效率以及滿意度是物流企業(yè)構(gòu)建聯(lián)盟的主要目的之一，物流企業(yè)的物流服務能力也是聯(lián)盟利益分配的重要影響因素。物流服務能力直接體現(xiàn)在物流服務質(zhì)量上，主要包括企業(yè)職能服務質(zhì)量和人力資源服務質(zhì)量。其中，企業(yè)職能服務質(zhì)量主要包括貨物運輸效率、物流服務時效、財務控制效率、成本控制效率等指標。人力資源服務質(zhì)量主要指信息服務效率、工作效率、客戶服務滿意度等相關(guān)指標。

在構(gòu)建物流聯(lián)盟利益分配模型中，以Shapley值法分析物流聯(lián)盟成員的貢獻度，運用TOPSIS法對物流聯(lián)盟下的其他多指標進行綜合評價。因此，為合理地對物流聯(lián)盟利益分配影響因素進行綜合評價，本文將以Shapley值法下的利益分配模型反映物流企業(yè)的邊際貢獻度，通過TOPSIS法對承擔風險、投資額、任務量、物流服務能力等四項因素進行綜合評價，以確定物流聯(lián)盟的利益分配系數(shù)。最后對兩種利益分配方法下的利益分配確定相應權(quán)重，以確定各項指標綜合評價下的物流聯(lián)盟利益分配模型。

三、TOPSIS&Shapley值法的利益分配模型

（一）Shapley值法

Shapley值法是由Shapley L.S提出用以解決多人合作博弈問題的數(shù)學方法，是一種考慮聯(lián)盟內(nèi)部成員博弈的利益分配方法，其原理是根據(jù)聯(lián)盟各成員為聯(lián)盟體帶來的利益增加值，以邊際貢獻為依據(jù)進行聯(lián)盟利益分配[15]。本研究運用此方法對n個物流企業(yè)組建物流聯(lián)盟的合作利益進行分配，對Shapley值法有以下假設和定義[13]：

假設物流聯(lián)盟體由n家物流企業(yè)組建，構(gòu)建的聯(lián)盟成員集合I={1，2，…，n}，且對于物流聯(lián)盟集合I中的任一子集si，均有與之對應的實數(shù)函數(shù)v （si）。其中，對于實數(shù)函數(shù)v（si）有以下規(guī)定：

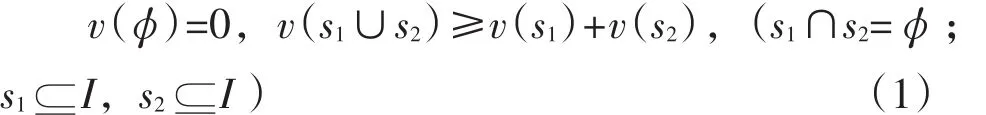
則稱v（si）是滿足I集合的對策函數(shù)。

假定xi為合作聯(lián)盟I中聯(lián)盟成員i所獲取的最大利益分配額，則可得利益分配額組合數(shù)列x=（x1，x2，…，xn）。同時，假設v（i）表示聯(lián)盟中的各成員獨自經(jīng)營獲取的利益，則規(guī)定以上變量滿足：

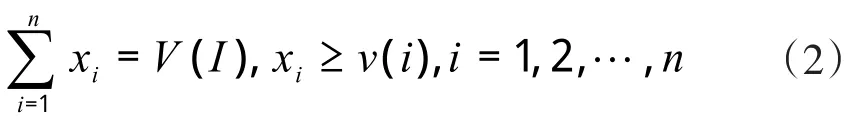
根據(jù)各變量滿足的條件可知，聯(lián)盟成員取得的利益分配額與聯(lián)盟體的總利益額相等，即滿足累加的性質(zhì)；同時，聯(lián)盟成員在聯(lián)盟下取得的利益額高于獨立經(jīng)營取得利益額，即為滿足合理性。設φi（v）表示在聯(lián)盟I下，成員i獲取的利益分配額，可得聯(lián)盟下的利益分配集合為Φ（v）=[φ1（v），φ2（v），…，φn（v）]，則有：

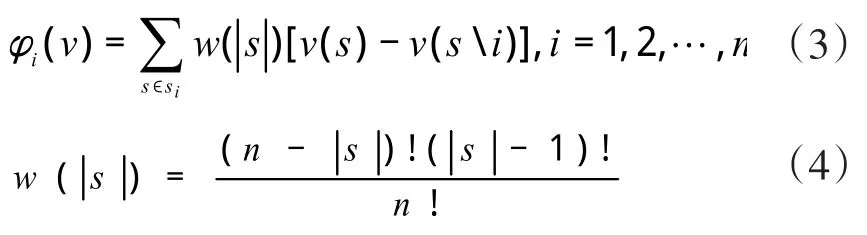
在（3）（4）式中，S表示聯(lián)盟集合I可形成的所有子集。其中，|S|表示子集S中的成員個數(shù)，n為集合I中的成員個數(shù)。w（|s|）表示加權(quán)權(quán)重，v（s）表示在子集S所獲取的利益額，v（si）表示子集S排除成員i所獲取的利益額。

Shapley值法的聯(lián)盟利益分配模型克服了利益平均分配問題，凸顯個體成員在聯(lián)盟中的重要性，且有利于激發(fā)成員積極性，但是Shapley值法也有一定缺陷。首先，假定聯(lián)盟集合的各個子集組合是隨機的，即為聯(lián)盟成員地位相同的假設與現(xiàn)實情況不符；其次，假定聯(lián)盟成員承擔的風險均為1/n，難以反映實際聯(lián)盟風險承擔情況；最后，忽略了各個成員為組建聯(lián)盟所做的其他貢獻，比如投入資源、任務承擔、服務質(zhì)量等。而對于物流聯(lián)盟來說，這些因素尤為重要。因此，為完善Shapley值法下的利益分配，為物流聯(lián)盟構(gòu)建更加合理的利益分配機制，本研究選取TOPSIS法對其修正。

（二）TOPSIS法

TOPSIS由Hwang和Yoon于1981年首次提出，是一種多變量、多目標的決策方法，通過測度備選方案的逼近理想解距離，實現(xiàn)對各方案優(yōu)劣排序，已被廣泛用于各個決策領域，其核心思想是根據(jù)求得的決策目標正理想解與負理想解來計算各方案的歐式距離，并得到各方案的相對貼近度；其中，相對貼近度越大的方案越優(yōu)，據(jù)此實現(xiàn)對各個方案的優(yōu)劣排序，此方法不僅具有計算簡單、結(jié)果合理的優(yōu)勢，而且能夠?qū)崿F(xiàn)對多指標的定量評價[15]。因此，借助此方法能夠可對物流聯(lián)盟成員邊際貢獻度以外的其他指標進行評價，運用TOPSIS法有以下假設及步驟：

1.原始數(shù)據(jù)標準化處理。設物流聯(lián)盟中有m個企業(yè)，選取n個一級評價指標，并假設xij為聯(lián)盟成員在指標j上的所得評分，則有原始矩陣為A：

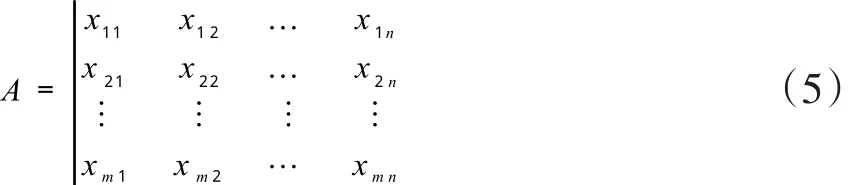
為實現(xiàn)對原始矩陣A的標準化處理，假設yij為標準化處理后的對應矩陣元素，并設標準化后的矩陣為B，則有：

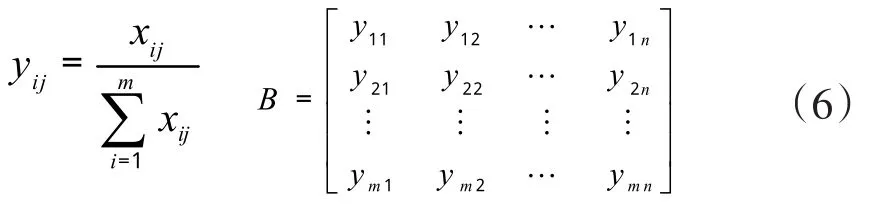
2.正理想解與負理想解。根據(jù)確定的標準化矩陣B可得各家物流企業(yè)在相對應評價指標的正理想解yj+與負理想解yj-，并設y+、y-分別為正理想解數(shù)列與負理想解數(shù)列，有表達式：

3.歐式距離以及相對貼近度。利用（7）（8）所求得的正、負理想解，并假設聯(lián)盟成員i的正歐式距離為Di+、負歐式距離為Di-、相對貼近度為Ci，則有：

根據(jù)（9）式計算的相對貼近度，可構(gòu)建與各聯(lián)盟成員相對應的相對貼進度數(shù)列，設為C，則有C={c1，c2，…，cn}。并將其標準化處理，則可得各聯(lián)盟成員的權(quán)重因子數(shù)列β={μ1，μ2，…，μn}。最后可根據(jù)各聯(lián)盟成員的權(quán)重因子確定其利益分配額，設為γi聯(lián)盟成員i所分的利益，V（I）為整個聯(lián)盟實現(xiàn)的利益額，有γi=μi·V（I）。

下面對可能影響矩形空心墩變形能力的參數(shù)進行敏感性分析，孫治國等通過有限元模擬，采用位移角作為延性目標對圓形空心墩的延性性能進行了研究。但國內(nèi)對于橋梁結(jié)構(gòu)而言，一般采用位移延性能力作為檢驗墩柱延性能力的指標。固本文采用位移延性能力作為延性指標，對縱筋配筋率、壁厚、軸壓比及縱筋強度等參數(shù)對矩形空心墩抗震能力的影響。

（三）綜合因子下的利益分配

在以上分析中，分別利用Shapley值法和TOPSIS法構(gòu)建聯(lián)盟利益分配模型。其中，Shapley值法主要關(guān)注聯(lián)盟成員邊際貢獻度，確定其在聯(lián)盟體中的重要性，以此計算聯(lián)盟成員i的利益分配額為φi（I）。針對Shapley值法的缺陷，借助TOPSIS法對聯(lián)盟成員除邊際貢獻度以外的、為構(gòu)建聯(lián)盟體所作努力的其他因素進行綜合評價，以此確定各聯(lián)盟成員的利益分配權(quán)重因子，并計算聯(lián)盟成員i的利益分配額為γi。

根據(jù)Shapley值法和TOPSIS法下確定各聯(lián)盟成員獲取的利益分配額，為實現(xiàn)聯(lián)盟成員為構(gòu)建聯(lián)盟所作努力的綜合評價，假設Shapley值法下的利益分配權(quán)重為α，則有聯(lián)盟成員i最終的利益分配額為：

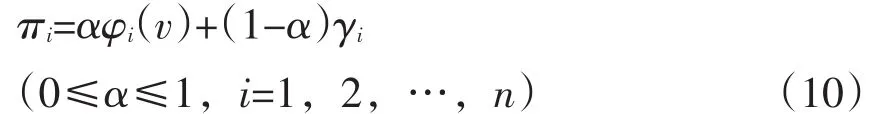
四、算例分析

為驗證所構(gòu)建物流聯(lián)盟利益分配模型的合理性，假設A、B、C三家物流企業(yè)組建物流聯(lián)盟體，并設定各物流企業(yè)獨立經(jīng)營、任意兩者結(jié)合經(jīng)營以及三者構(gòu)建物流聯(lián)盟的利益額已知，通過Shapley值法與TOPSIS法對物流聯(lián)盟利益分配進行分析。

（一）Shapley值法的利益分配

為確定不同合作機制下的物流企業(yè)貢獻額，假設物流企業(yè)A單獨經(jīng)營能夠獲取利益20萬，物流企業(yè)B獨自經(jīng)營能夠獲取利益30萬，物流企業(yè)C獨自經(jīng)營能夠獲取利益40萬。另假設，物流企業(yè)A、B聯(lián)合運營能夠獲取利益80萬；物流企業(yè)A、C聯(lián)合運營能夠獲取利益90萬；物流企業(yè)B、C聯(lián)合運營能夠獲取利益120萬；物流企業(yè)A、B、C組建物流聯(lián)盟能夠獲取利益160萬。根據(jù)Shapley值法下的聯(lián)盟利益分配，物流企業(yè)A在不同聯(lián)合運營模式下的相關(guān)利益統(tǒng)計數(shù)據(jù)見表1。

根據(jù)表1中的相關(guān)數(shù)據(jù)，并依據(jù)公式φ（iv）=，可求得在三家物流企業(yè)組建物流聯(lián)盟下，物流企業(yè)A依據(jù)Shapley值法的利益分配模型獲取的利益分配額為φ（Av）=36.67萬。以此方法類求，可得物流企業(yè)B和物流企業(yè)C在物流聯(lián)盟下的利益分配額分別為φ（Bv）=56.66萬、φ（Cv）= 66.67萬。根據(jù)求得的物流企業(yè)A、B、C在物流聯(lián)盟下的利益分配額有φA（v）+φB（v）>v（A∪B）、φA（v）+φ（Cv）>v（A∪C）、φ（Cv）+φ（Bv）>v（B∪C），均滿足Shapley值法下的利益分配條件。

（二）TOPSIS法的利益分配

通過Shapley值法對物流企業(yè)A、B、C的邊際貢獻度進行衡量，并以此確定三家物流企業(yè)在物流聯(lián)盟下的利益分配額。為確定各物流企業(yè)在風險、投資額、任務量、服務能力等四個一級指標下的權(quán)重，通常情況是根據(jù)相關(guān)專家以及物流企業(yè)之間的協(xié)商確定，并利用TOPSIS法綜合評價。

1.原始數(shù)據(jù)以及規(guī)范化處理。在風險承擔的量化上以1～9數(shù)字為風險等級，數(shù)字越大風險越高；投資額按照各物流企業(yè)的實際情況核算、任務量主要依據(jù)物流企業(yè)的營業(yè)額確定；服務能力則主要依據(jù)物流企業(yè)的現(xiàn)代化管理水平、企業(yè)組織結(jié)構(gòu)以及成本控制水平等確定。在本研究中，對物流企業(yè)A、B、C在四項指標的量化值假設見表2。

利用（5）式對原始數(shù)據(jù)進行規(guī)范化處理可得相關(guān)規(guī)范化矩陣B為：

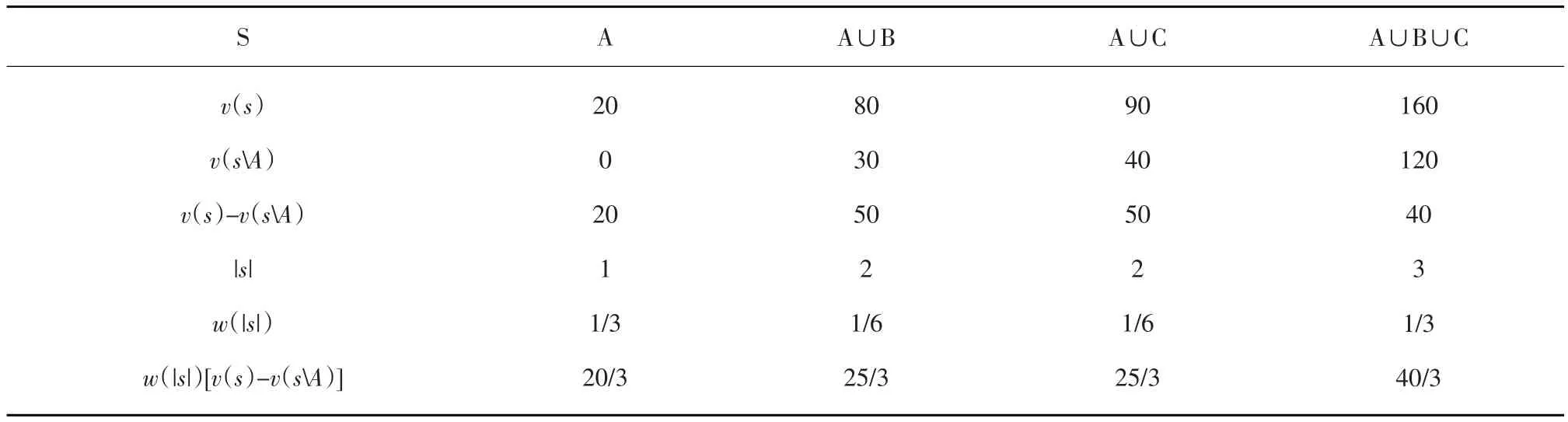
表1　物流企業(yè)A基于Shapley值法的利益分配

表2　物流企業(yè)各指標原始數(shù)據(jù)

2.正理想解與負理想解。根據(jù)確定的標準化矩陣，可計算各個評價指標的下的正理想解y+與負理想解y－，有數(shù)列表達式為：

3.歐式距離以及相對貼近度。利用（11）求得的正、負理想解，以及利用公式（9）求得的物流企業(yè)A、B、C的正、負歐式距離和相對貼近度相關(guān)數(shù)據(jù)如表3所示。

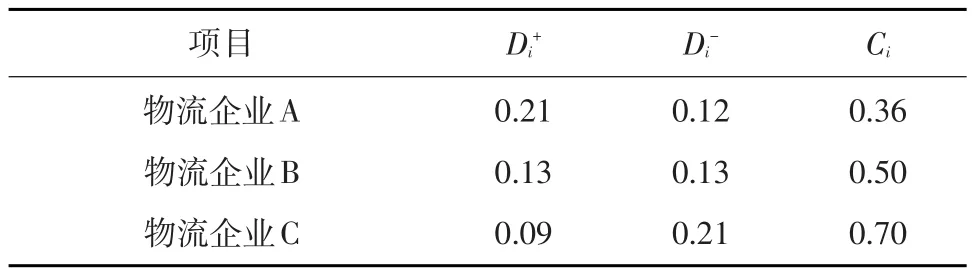
表3　TOPSIS法的物流企業(yè)相關(guān)指標數(shù)據(jù)

根據(jù)表3數(shù)據(jù)，將物流企業(yè)A、B、C的相對貼近度規(guī)范化處理，可得三家物流企業(yè)聯(lián)盟，以風險、投資額、任務量、服務能力等四項一級評價指標下的利益分配權(quán)重。設權(quán)重因子為μi，權(quán)重數(shù)列為β，則有β={μA，μB，μC}={0.23，0.32，0.45}。依據(jù)權(quán)重因子，可得在TOPSIS法下的物流企業(yè)所實現(xiàn)利益分配額為γ={γA，γB，γC}={35.8，51.2，72}。

（三）綜合利益分配

在以上分析中，利用Shapley值法和TOPSIS法實現(xiàn)物流企業(yè)A、B、C搭建的聯(lián)盟體下的利益分配。其中，Shapley值法側(cè)重于分析三家物流企業(yè)的邊際貢獻度，而TOPSIS法對三家物流企業(yè)的風險、投資額、任務量、服務能力等指標進行評價。為實現(xiàn)聯(lián)盟下的物流企業(yè)A、B、C的綜合分析，以確定最終的聯(lián)盟利益分配額，在本研究中，假設利用Shapley值法的利益分配權(quán)重為0.6，TOPSIS法下的利益分配權(quán)重為0.4，則根據(jù)公式（10），可得物流企業(yè)A、B、C構(gòu)建聯(lián)盟所實現(xiàn)的利益分配額分別為：

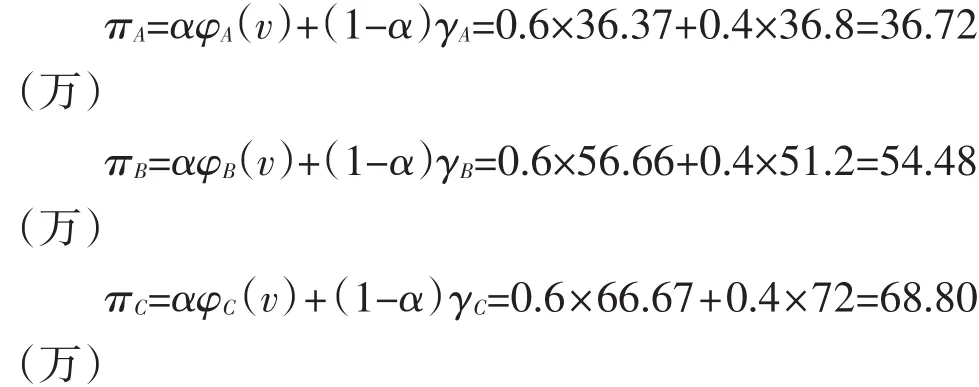
綜上，利用Shapley值法與TOPSIS法結(jié)合的利益分配方法構(gòu)建物流聯(lián)盟的利益分配模型。且在算例分析中，假設有三家物流企業(yè)組建物流聯(lián)盟以及相關(guān)變量假設，計算得出物流企業(yè)成員的利益分配額。

五、總結(jié)

合理、公平的利益分配是聯(lián)盟保持穩(wěn)定運營的基礎，本文利用Shapley值法與TOPSIS法結(jié)合的方法為物流聯(lián)盟搭建體現(xiàn)綜合因素權(quán)重的利益分配模型。其中，Shapley值法體現(xiàn)物流企業(yè)成員的重要性，依據(jù)物流企業(yè)為聯(lián)盟利益增值所做的邊際貢獻（營業(yè)額、利潤額等指標體現(xiàn)）進行利益分配。另外，組建聯(lián)盟的物流成員具有不同的屬性，面臨風險也不盡相同。因此，為實現(xiàn)物流聯(lián)盟利益分配模型的優(yōu)化，采用應用廣泛、操作簡便、結(jié)果可靠的TOPSIS綜合評價方法對物流企業(yè)成員的風險、投資額、任務量、服務能力等四項關(guān)鍵指標進行綜合評價，以此確定物流企業(yè)成員在聯(lián)盟體制下的利益分配的權(quán)重因子。

另外，研究通過算例分析驗證了所構(gòu)建的物流聯(lián)盟利益分配模型的可行性。結(jié)果顯示，構(gòu)建的物流聯(lián)盟利益分配方法不僅克服了利益平均分配的不合理問題，而且將物流企業(yè)成員為搭建聯(lián)盟的多個關(guān)鍵性努力因素納入了聯(lián)盟利益分配考慮之中，所計算出的利益分配結(jié)果具有合理性。構(gòu)建的物流聯(lián)盟利益分配模型更易被聯(lián)盟成員所接受，有利于實現(xiàn)物流聯(lián)盟的可持續(xù)運營。

參考文獻:

［1］徐揚,申金升,王傳濤.物流聯(lián)盟的形成機理與協(xié)作博弈研究[J].交通運輸系統(tǒng)工程與信息,2011(2).

［2］Lunnan R,Haugland S A.Predicting and Measuring Alliance Performance[J].Strategic Management Journal,2008(5).

［3］吳朗.產(chǎn)出分享模式下動態(tài)物流聯(lián)盟利益分配方法[J].系統(tǒng)工程,2009(5).

［4］魏瑋.戰(zhàn)略聯(lián)盟組織的穩(wěn)定性、組織治理與信用約束機制[J].經(jīng)濟管理,2006(8).

［5］杜義飛,李仕明,陳德富.價值創(chuàng)造結(jié)構(gòu)、K-重劃分與聯(lián)盟穩(wěn)定性變化研究[J].管理工程學報,2012(1).

［6］徐揚,申金升,王傳濤.物流聯(lián)盟的形成機理與協(xié)作博弈研究[J].交通運輸系統(tǒng)工程與信息,2011(2).

［7］江琳琳.基于BP神經(jīng)網(wǎng)絡的物流戰(zhàn)略聯(lián)盟風險評估研究[J].科技管理研究,2011(24).

［8］靳慧斌,劉明廣.一種全因素的動態(tài)聯(lián)盟利潤分配機制設計[J].統(tǒng)計與決策,2007(20).

［9］馬小龍.物流聯(lián)盟內(nèi)部利益分配問題的分析[J].交通科技與經(jīng)濟,2012(6).

［10］甘家華,王建偉,陳卓,等.質(zhì)量導向下的中小物流企業(yè)聯(lián)盟收益分配策略[J].技術(shù)經(jīng)濟與管理研究,2014(10).

［11］易欣,張飛漣,邱慧,等.不確定AHP和Shapley值應用于投標聯(lián)合體利益分配[J].計算機工程與應用,2012(27).

［12］李靚,劉征馳,周堂.基于Shapley值修正算法的聯(lián)盟企業(yè)利潤分配策略研究[J].技術(shù)與創(chuàng)新管理,2009(6).

［13］楊晶,江可申,邸強.基于TO PSIS的動態(tài)聯(lián)盟利益分配方法[J].系統(tǒng)工程,2008(10) .

［14］顧桂蘭.基于TOPSIS的協(xié)同商務利益分配機制研究[J].企業(yè)經(jīng)濟,2011(3).

［15］謝識予.經(jīng)濟博弈論[M].上海:復旦大學出版社,2006.

［16］HWang C L,Yoon K S.Multiple Attribute Decision Making[M].Berlin: Spring-Verlag,1981.

作者簡介：林翊（1973-），男，福建師范大學經(jīng)濟學院副教授，研究方向為產(chǎn)業(yè)組織與產(chǎn)業(yè)政策、企業(yè)管理。

基金項目：教育部人文社會科學青年基金項目“制造業(yè)與物流業(yè)聯(lián)動發(fā)展的機理與模式研究——基于產(chǎn)業(yè)共生理論”（12YJC630220）

中圖分類號：F224

文獻標識碼：A

文章編號：1672-3805(2016)01-0032-06

收稿日期：2016-01-13