基于三階剪切形變理論的復合層合矩形板水下聲輻射研究

胡昊灝，高 巖

（中國船舶科學研究中心 a.船舶振動噪聲重點實驗室；b.江蘇省綠色船舶技術重點實驗室，江蘇 無錫 214082）

基于三階剪切形變理論的復合層合矩形板水下聲輻射研究

胡昊灝a，b，高 巖a，b

（中國船舶科學研究中心 a.船舶振動噪聲重點實驗室；b.江蘇省綠色船舶技術重點實驗室，江蘇 無錫 214082）

以簡化的三階剪切形變理論為基礎，由虛功原理建立了較厚復合層合矩形板水下振動與聲輻射方程，通過Rayleigh-Ritz法求解系統方程。為了驗證所給方法的正確性將計算結果與有限元法計算結果進行對比，并將三階剪切形變理論（TSDT）所得聲輻射解與一階剪切形變理論（FSDT）計算結果進行對比，指出前者在計算復合層合板聲輻射上的優勢。最后通過改變楊氏模量，剪切模量，鋪層厚度，纖維鋪設角等參數，指出影響復合層合板聲輻射的主要因素和分頻段變化規律，可為水下典型結構聲輻射預報和噪聲控制提供參考。

三階剪切形變；復合層合板；聲輻射；噪聲控制

0 引 言

復合層合材料具有輕質高強，耐腐蝕等優良特性，因而被廣泛地應用于船舶工業中。由于復合材料本身構成的復雜性，其動力學特性要遠復雜于各向同性材料[1]。

近年來，對復合層合材料動力學的研究主要分為兩類方法，第一類是以三維彈性理論為基礎的研究[2]，該方法需要建立各層彈性力學方程，結合應力應變的邊界條件以及連續性條件聯合求解，由于沒有對應力分布作任何假設，計算極其繁瑣，只有當層數很少，加載方式邊界條件都很簡單時才能求解。另一類則是以二維彈性理論為基礎，包括經典層合板理論（CLPT）[3]、一階剪切形變理論（FSDT）[4-6]、高階剪切形變理論（HSDT）[7]和離散層理論[8]等方法，它們是在三維彈性理論的基礎上對沿厚度方向的應力分布作適當假設而得到的，吳梵[9]在求解正交加筋復合夾層板的彎曲問題時，對面板和底板采用基于Kirchhoff假設的CLPT理論，而對芯層采用基于mindlin模型的FSDT理論。Daneshjou[10-11]也利用這兩種理論求解了無限長復合層合圓柱殼的隔聲量問題，Cao[12]用FSDT理論求解了無限加雙周期肋骨平板的遠場聲壓。CLPT理論忽略了剪切和轉動慣量，僅適合薄板，FSDT是目前應用最多的，但該理論假設沿厚度方向的剪切應變為常數，需要引入剪切修正因子，而事實上剪切修正因子的獲取較復雜。考慮到經典層合板理論與一階剪切形變所存在的問題，本文采用簡化的三階剪切形變理（TSDT）論來分析復合層合矩形板的聲輻射問題，該方法將位移場用厚度坐標的三次方展開，更能真實地反映層間應力分布，所含未知數個數與一階剪切形變理論相同，且不需要引入剪切修正因子。

以往的文獻關于有限大彈性薄板聲輻射的研究已經很成熟[13]，但關于復合層合板（尤其是有限大復合層合板）的聲輻射問題，由于其動力學模型的復雜性和應用隱秘性而鮮有涉及，本文利用變分法首先建立復合層合板水下聲輻射模型，然后求解并分析材料參數和幾何參數對輻射噪聲的影響，最后給出了一些有意義的結論，為水下典型結構聲輻射預報提供參考。

1 模型描述

如圖1所示，取一由纖維加強的復合層合矩形板，將其四條邊均簡支于無限大剛性障板上，板的上側為無限大水域，下側為真空，考慮在機械點力激勵下復合板的聲輻射問題。

1.1 位移場

圖1 復合層合板聲輻射示意圖Fig.1 The schematic of sound radiation for laminated composite plate

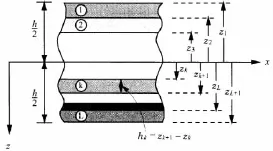
圖2 復合層合矩形板各層橫向分布Fig2 The transverse distribution for each layer

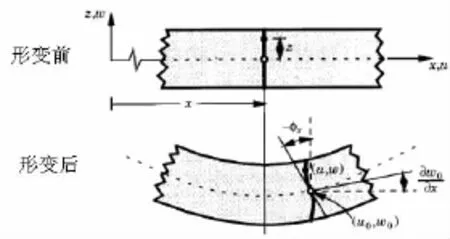
圖3 復合層合板位移形變Fig3 The deformation of the plate

結合圖2，圖3，將位移展開為厚度坐標的三次函數形式，即：

其中：u0、v0和w0為中性面上的位移，φx、φy、θx、θy、λx和λy為待定參數。

θx、θy、λx和λy可以通過層合板上表面和下表面的剪切應力自由的邊界條件[7]求得，即：

經過化簡后位移場僅含五個未知變量，這與一階剪切形變理論（FSDT）所包含的未知數是一樣的。

其中：系數c1=4/3h2（h為板的總厚度）。

1.2 非線性應變場

與三階剪切形變位移理論對應的復合層合板的應變場可由Von Karman非線性理論給出：

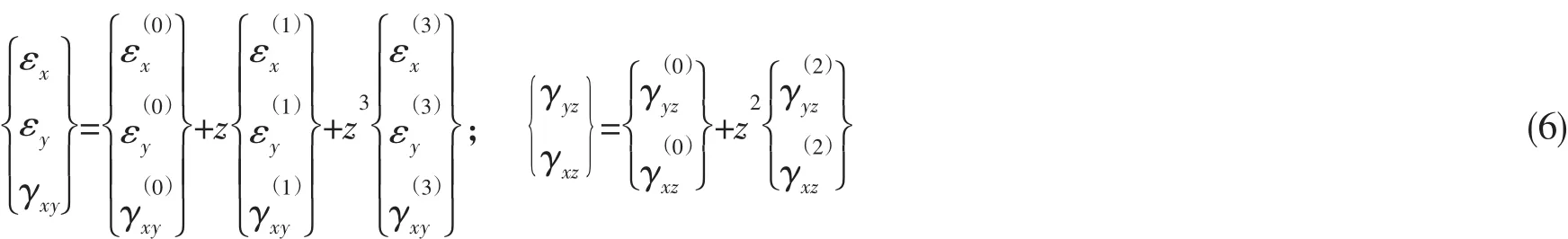
1.3 合成應力及合成力矩

其中：N表示面內合成應力，M表示合成力矩，P、Q和R表示高階合成應力，A、B、D、E、F和H為不同類型的剛度矩陣。

1.4 流載聲壓

無限大水域中的聲壓p滿足Helmholtz方程：

其中：k0=ω/c0為聲場波數，c0為水中聲速。

在復合層合板與流體接觸表面滿足法向振速連續性：

通過求解方程聲場聲壓的表達式可由Rayleigh積分給出：

其中：ρ0為流體密度，為板表面振速，R為板表面上的點與場點的距離。

2 系統運動方程與方程求解

利用Hamilton原理（即虛功原理）可知：

符號δ表示變分，V，T和Wex分別為系統應變能、動能以及外力做功。將應力、應變以及位移表達式（3）-（8）代入（14）式，然后利用分部積分使虛位移δu0、δv0、δw0、δφx和δφy分離出來且令它們的系數為0，即可得到系統的Euler-Lagrange運動方程：

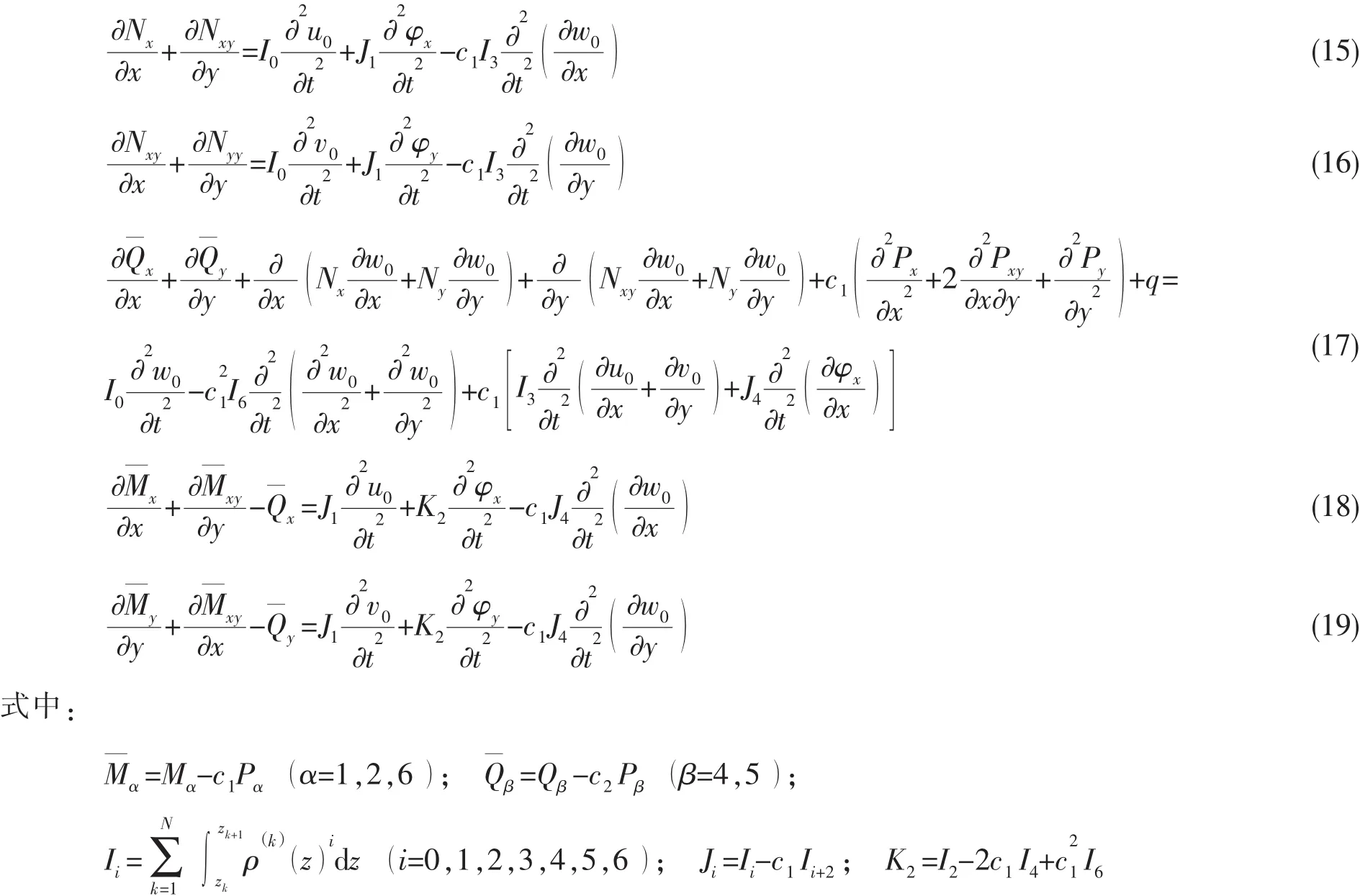
其中：q表示作用在復合層合板上的激勵，在這里q=F-p，F表示諧和點激勵F=F0δ（x-x0）（y-y0），p表示板表面流體載荷聲壓，其表達式由Rayleigh積分（13）給出。

2.1 Rayleigh-Ritz解

以反對稱角鋪設纖維材料的復合層合板為例，當滿足四邊簡支邊界條件時形式解可設為：

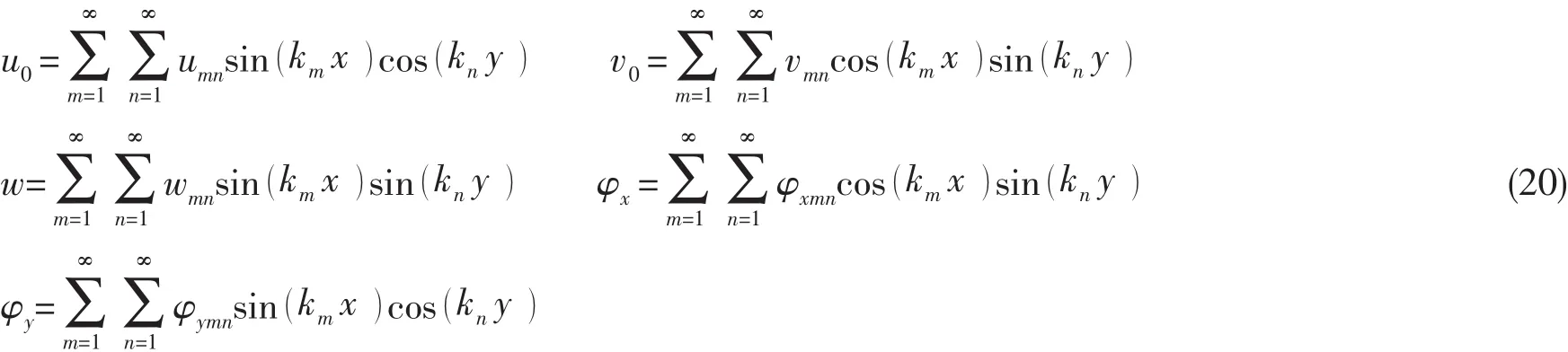
其中：km=mπ/a，kn=nπ/b

式中：Sij、mij分別為剛度矩陣和質量矩陣，pmn為聲壓模態幅值：

Zmnpq為復合層合板表面輻射聲阻抗，其表達式為：

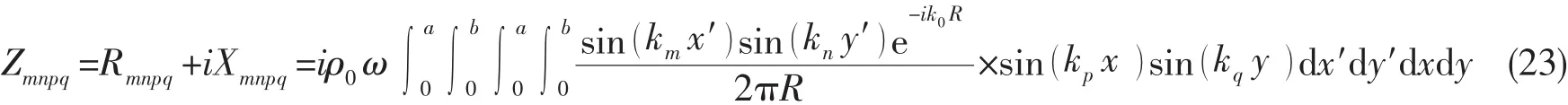
求解系統運動方程（21）可得到夾芯板橫向位移模態幅值wmn，進一步可得到系統的均方振速以及輻射聲功率表達式。

3 模型驗證與參數分析

所分析復合層合板由六層單層板構成，各層厚度相等均為h=0.002（m），板長度a=0.6（m），寬b= 0.6（m），為了計算方便，假設各層材料相等，纖維鋪設角度分別為 ［45°/-45°/45°/-45°/45°/-45°］。楊氏模量E1=1.2×1011（Pa），E2=1×1010（Pa）；泊松比υ12=0.4，υ21=0.4；剪切模量G12=G23=5.9×109（Pa），G13=3× 109（Pa）；各層材料密度均為1 600（kg/m3）。激勵點位置為（0.3 m，0.2 m），激勵力幅值為1（N）。振速參考級為5×10-8（m/s），輻射聲功率參考級為0.67×10-18（w）。

3.1 算法驗證

以往的文獻中關于有限復合層合板聲輻射的計算很少，為了驗證所建模型的正確性，本文利用有限元商業軟件Ansys計算模型的均方振速，取復合層合材料Solid186單元來進行對比驗證，Solid186單元為20節點三維實體單元，每個節點有三個自由度，位移按厚度坐標的二次方展開，支持材料的非線性行為和大形變與三階剪切形變理論（TSDT）比較接近。圖4給出了用兩種方法計算的復合層合板均方振速對比圖，從圖中可以看出兩者具有較好的一致性。

圖5為上述模型分別采用一階剪切形變理論（FSDT）和三階剪切形變理論（TSDT）計算的輻射聲功率，由圖可看出在600 Hz以下的頻帶內，兩者輻射聲功率級完全一致，這是因為在低頻范圍所分析波長遠大于厚度，此時剪切形變和轉動慣量對聲輻射影響很小，隨著頻率的增加兩者的差別開始增大，FSDT遺漏了較多的模態峰值，一方面是因為對于較厚的復合層合板高階剪切應力和轉動慣量會對聲輻射起到一定作用，另一方面由于FSDT理論中剪切修正因子的選取差別也會帶來一定的誤差，這也進一步說明了TSDT理論能更準確地反映材料內部應力分布。

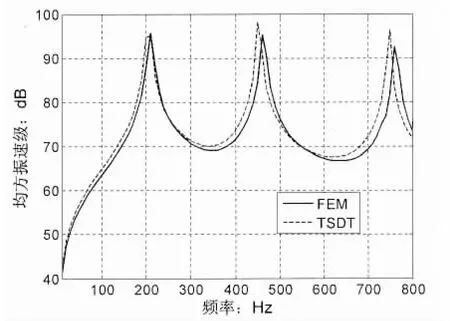
圖4 模型均方振速驗證Fig4 Validation of model mean square power of velocity

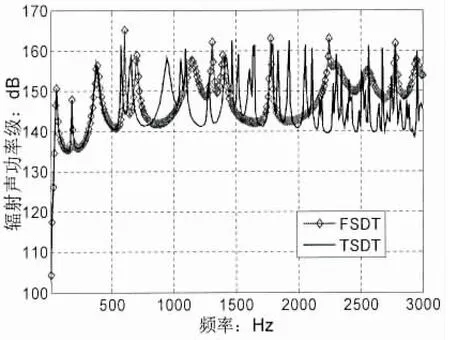
圖5 FSDT與TSDT輻射聲功率對比Fig 5 Comparison between the sound radiated FSDT and TSDT

3.2 參數分析

3.2.1 彈性模量對聲輻射的影響

為了能簡單而有效地說明彈性模量對聲輻射的影響，取一單層正交各向異性復合板，厚度為0.006（m），鋪層角度為45°，其余參數同上文一致。圖6分析了材料參數E1、E2、G12和G13對聲輻射的影響，由公式（9）和（10）可知這四個量將影響拉壓剛度A、彎曲剛度D以及高階剛度F、H等，因此其變化規律對聲輻射的影響要遠復雜于各向同性材料。從圖中可看到在低頻范圍內（500 Hz以內），改變G12和G13對輻射聲功率的影響很小，而改變E1和E2則有明顯的頻率峰值偏移，且峰值大小也有所改變。在中高頻范圍，改變E1、E2、G12和G13均會產生頻率峰值偏移和大小改變，但是改變E1和E2，輻射聲功率級大小變化在5 dB到10 dB左右，而改變G12和G13時輻射聲功率級的起伏在5 dB以下。因此說，改變不同方向的楊氏模量E1和E2對聲輻射的影響要大于改變剪切模量G12和G13對聲輻射的影響，從整體上來說增加材料楊氏模量，系統的輻射聲功率水平下降，這主要是影響了彎曲剛度，然而在某些區域隨著楊氏模量增加反而會增加輻射聲功率，因為楊氏模量的增加會改變其它剛度。剪切模量對中低頻區域影響很小，僅在高頻段有一定影響，這是因為在低頻段剪切形變相對于分析波長可以忽略。

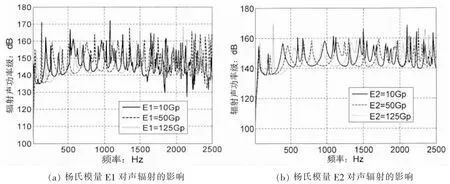
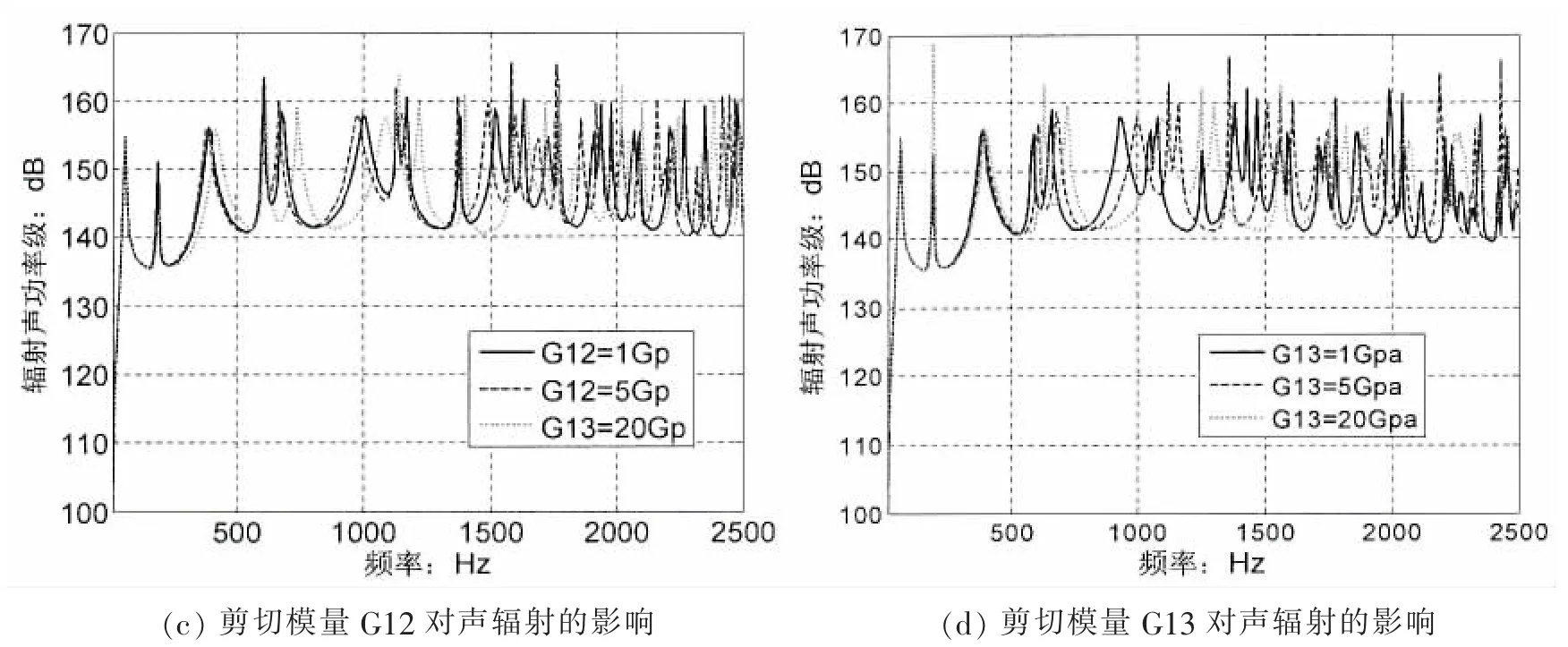
圖6 材料參數對聲輻射的影響Fig.6 Effects of material parameters to sound radiation

3.2.2 鋪層厚度和鋪設角對聲輻射的影響

如圖7所示，隨著復合層合板厚度的增加，大部分頻帶內的輻射聲功率級均有所下降，模態峰值存在頻率偏移，且在中高頻段能有效抑制掉部分諧振模態峰，這種厚度對聲輻射的影響規律與均勻各向同性金屬板是一致的，但由于復合層合材料的密度較金屬板小很多，所以即使增加厚度也不會帶來過多質量增加。因此增加復合層合板的厚度是有效降低輻射噪聲的手段。

圖8為纖維鋪設角對聲輻射的影響，由此可以看出聲輻射隨鋪設角度的變化關系比較復雜，由（10）式可知，鋪設角θ主要影響轉換剛度系數，θ與各類剛度系數均有較復雜的關系，因此不能籠統的概括改變鋪設角對聲輻射的影響，整體而言45°時平均輻射聲功率級較小，可以根據具體需要，在不同頻段內對鋪設角進行設計。

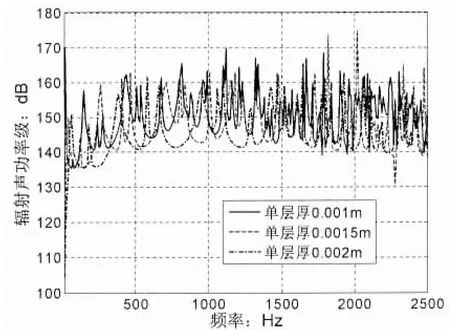
圖7 鋪層厚度對聲輻射的影響Fig.7 Effects of lamina thickness

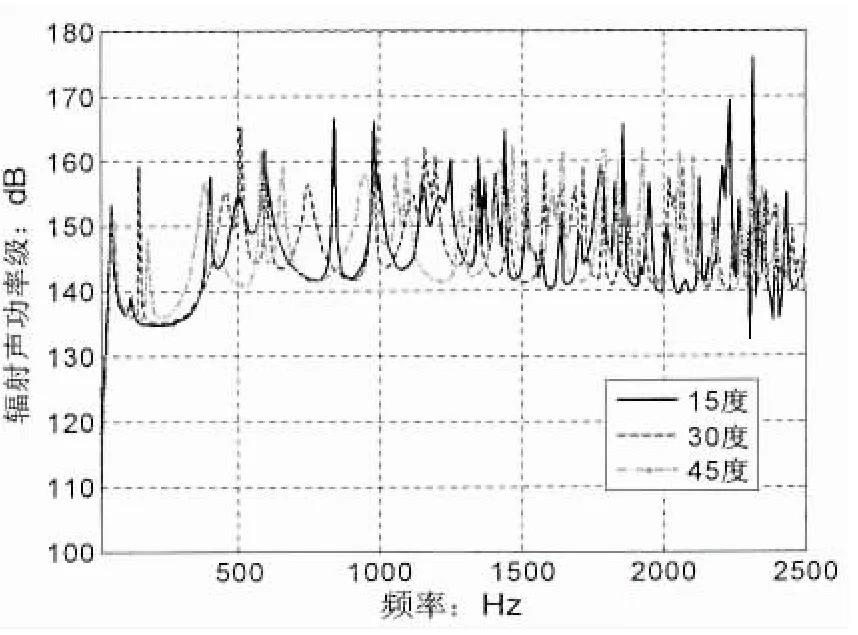
圖8 纖維鋪設角對聲輻射的影響Fig.8 Effects of fiber orientation angle

4 結 論

本文利用三階剪切形變理論，采用變分法建立和推導了較厚復合層合矩形板水下聲輻射模型，通過與有限元法計算結果對比驗證了所給算法的正確性，最后分析了不同參數對聲輻射的影響，得到如下結論：

（1）由于要考慮高階剪切和轉動慣量，基于TSDT的復合層合板聲輻射系統運動方程的推導要復雜于CLPT和FSDT，但利用表面應力自由條件可使系統運動方程維數與FSDT相同，且不需要剪切修正，在中高頻率范圍，采用TSDT的聲輻射計算精度更高。

（2）材料參數對復合層合板聲輻射的影響要遠復雜于各向同性材料情況，楊氏模量E1和E2對聲輻射的影響要大于剪切模量G12和G13，后者僅在高頻段有影響。可以根據不同的設計要求，改變材料參數而實現噪聲優化。

（3）復合層合板鋪層厚度與鋪設角是影響聲輻射的重要參數，增加鋪層厚度在大部分頻段內能有效地降低輻射聲功率級，而鋪設角由于影響各類剛度轉換系數對聲輻射的影響規律較為復雜，45°時平均輻射聲功率級較小。

[1]Qatu M S.Vibration of laminated shells and plate[M].Amsterdam：Elsevier Academic Press,2004.

[2]Berry A,Foin O,Szabo J P.Three dimensional elasticity model for a decoupling coating on a rectangular plate immersed in a heavy fluid[J].Journal of the Acoustical Society of America,2001,109(6)：2704-2714.

[3]Yin X W,Gu X J,Cui H F,et al.Acoustic radiation from a laminated composite plate reinforced by doubly periodic parallel stiffeners[J].Journal of Sound and Vibration,2007,306：877-889.

[4]Ramachandran P,Narayanan S.Radiation efficiency of a composite cylindrical shell[C]//20th International Congress on Sound&Vibration.Bangkok,Thailand,2013.

[5]Mejdi A,Legault J,Atalla N.Transmission loss of periodically stiffened laminate composite panels：Shear deformation and in-plane interaction effects[J].Journal Acoustical Society of America,2012,13(1)：174-185.

[6]楊 坤,梅志遠,李華東.粘彈性復合材料夾芯板穩態響應分析[J].振動與沖擊,2013,32(7)：88-92. Yang Kun,Mei Zhiyuan,Li Huadong.Steady response analysis for a composite sandwich plate with viscoelastic core layer based on kelvin model[J].Journal of Vibration and Shock,2013,32(7)：88-92.

[7]Lee S J,Reddy J N.Nonlinear deflection control of laminated plates using third-order shear deformation theory[J].International Journal of Mechanics and Materials in Design,2004,1：33-61.

[8]Ghinet S,Atalla N.Diffuse field transmission into infinite sandwich composite and laminate composite cylinders[J].Journal of Sound and Vibration,2006,289(4-5)：745-778.

[9]吳 梵,楊 坤,梅志遠,等.正交加筋復合材料夾層板彎曲問題求解[J].船舶力學,2013,17(1-2)：92-101. Wu Fan,Yang Kun,Mei Zhiyuan.Bending solution of orthogonally rib-stiffened composite sandwich plate[J].Journal of Ship Mechanics,2013,17(1-2)：92-101.

[10]Daneshjou K,Nouri A,Talebitooti R.Sound transmission through laminated composite cylindrical shells using analytical model[J].Arch Applied Mechanical,2007,77：363-379.

[11]Daneshjou K,Shokrieh M M,Moghaddam M G,et al.Analytical model of sound transmission through relatively thick FGM cylindrical shells considering third order shear deformation theory[J].Composite Structures,2010,93：67-78.

[12]Cao X T,Hua H X,Zhang Z Y.Sound radiation from shear deformable stiffened laminated plates[J].Journal of Sound and Vibration,2011,330(16)：4047-4063.

[13]沈 蘇,劉碧龍,李曉東,等.簡支矩形板模態輻射阻抗的一種快速計算方法分析[J].聲學學報,2010,35(2)：126-133. Shen Su,Liu Bilong,Li Xiaodong.An analysis of a fast calculation method of modal radiation reactance of a simplysupported rectangular panel[J].ACTA Acustica,2010,35(2)：126-133.

Sound radiation of underwater laminated composited rectangular plate using higher order shear deformation theory

HU Hao-haoa,b,GAO Yana,b
(a.National Key Laboratory on Ship Vibration&Noise;b.Jiangsu Key Laboratory of Green Ship Technology, China Ship Scientific Reaearch Center,Wuxi 214082,China)

Based on the simplified Third Order Shear Deformation Theory(TSDT),the vibration and sound radiation of moderate laminated composite rectangular plate were deduced,and the system motion equation was solved by Rayleigh-Ritz method.In order to validate the proposed method,the result was compared with the finite element method,and the advantage of calculating sound radiation was shown by comparing TSDT with FSDT.And by changing the Young’modulus,shear modulus,lamina thickness,fiber orientation angle,the main parameter and the variation in different frequency band were obtained,which could be a reference for underwater typical structure sound radiation and noise control.

third order shear deformation;laminated composite plate;sound radiation;noise control

TB535

：Adoi：10.3969/j.issn.1007-7294.2016.05.013

1007-7294（2016）05-0620-08

2016-02-27

國家自然科學基金資助項目（11274080）

胡昊灝（1983-）男，博士研究生，E-mail：huhaohao049@sohu.com；高 巖（1982-），女，高級工程師。