基于支持向量回歸機和粒子群算法的船舶操縱運動模型辨識

張心光，鄒早建，王巖松

（1.上海工程技術大學 汽車工程學院，上海201620；2.上海交通大學 船舶海洋與建筑工程學院，上海 200240；3.上海交通大學 海洋工程國家重點實驗室，上海 200240）

基于支持向量回歸機和粒子群算法的船舶操縱運動模型辨識

張心光1，鄒早建2，3，王巖松1

（1.上海工程技術大學 汽車工程學院，上海201620；2.上海交通大學 船舶海洋與建筑工程學院，上海 200240；3.上海交通大學 海洋工程國家重點實驗室，上海 200240）

基于仿真的Z形試驗數據，應用支持向量回歸機對船舶操縱運動響應模型進行了機理建模，從核函數結構中得到了模型中的操縱性指數，并利用建立的響應模型進行了Z形試驗的運動預報，同時引入粒子群算法對懲罰因子C值進行尋優，以減少懲罰因子C值選擇的任意性對船舶操縱運動模型辨識精度產生的不利影響。通過將運動預報結果同仿真試驗數據進行比較，驗證了文中方法的有效性。

船舶操縱；響應模型；參數辨識；支持向量回歸機；粒子群算法

0 引 言

應用船舶操縱運動數學模型加計算機模擬的方法進行船舶操縱性預報的關鍵是精確確定數學模型中的水動力導數和操縱性指數。目前采用的船舶操縱運動數學模型主要包括兩類：一類是水動力模型[1-2]；另一類是響應模型[3]。

目前，基于自航模試驗或實船試驗的系統辨識方法是求取船舶操縱運動水動力導數和操縱性指數的有效方法之一。極大似然（Maximal Likelihood，ML）估計法、模型參考自適應（Model Reference Adaptive，MRA）法等傳統的系統辨識方法曾被廣泛應用于船舶操縱運動建模研究中[4]。但是，這些系統辨識方法有一些固有缺陷，如，對數學模型的依賴性過大，對初值的依賴性過大等。基于人工智能技術的人工神經網絡能克服傳統系統辨識方法的缺陷，已被廣泛應用于船舶操縱運動建模研究中，例如，Ebada和Abdel-Maksoud應用BP神經網絡進行了回轉操縱性能預報研究[5]；Guedes Soares應用遞歸神經網絡進行了船舶操縱運動建模研究[6]。然而，人工神經網絡也有一些缺陷，如，泛化性能不足，存在局部極值問題和維數災難問題等。近二十幾年來，在系統辨識領域出現了一種新的人工智能方法—支持向量機（Support Vector Machines，SVM）[7-8]，該方法解決了在人工神經網絡中無法避免的局部極值問題和維數災難問題并具有很好的泛化能力。

當SVM用于參數辨識時，稱為支持向量回歸機（Support Vector Regression，SVR）。SVR包括最小二乘支持向量回歸機（Least Square-SVR，LS-SVR）、ε—支持向量回歸機（ε-SVR）、ν—支持向量回歸機（ν-SVR）等。Luo等[9]曾應用LS-SVR對操縱運動響應模型進行了參數辨識，并利用建立的響應模型對10°/10°和20°/20°Z形試驗進行了運動預報，通過將預報結果和自航模試驗結果進行比較，對所采用方法的有效性進行了驗證。SVR的結構參數包括懲罰因子C和不敏感因子ε。文獻[10]討論了不敏感因子ε對船舶操縱運動建模的影響，并給出了不敏感因子ε取值與SVR回歸精度的關系。但是，懲罰因子C值的選取目前尚缺乏理論依據，且對懲罰因子C值選取的研究，鮮有文獻報道，這嚴重影響了基于SVR的船舶操縱運動模型辨識精度。

本文將粒子群算法應用于懲罰因子C值的尋優，同時基于仿真得到的10°/10°、15°/15°Z形試驗數據，應用ε-SVR辨識了船舶操縱運動響應模型參數，并采用所建立的響應模型對10°/10°、15°/15°Z形試驗進行了運動預報，通過將首向角和轉艏角速度的預報結果同仿真試驗數據進行對比，驗證了本文方法的有效性。

1 方法介紹

本文應用ε-SVR辨識的響應模型包括一階線性響應模型和二階線性響應模型：

將方程（1）和（2）分別用前向差分離散化，得到：

式中：Δt為采樣間隔，a1、a2、b1和b2是待辨識的參數。

令T1T2=h，T1+T2=g，則a1、a2、b1、b2和h、g及操縱性指數K、T的關系為：

由方程（3）和（4）可分別得到訓練樣本對：

一階線性響應模型：

二階線性響應模型：

其中l為樣本數。

應用ε-SVR對上述響應模型進行參數辨識，其算法如下：

（2）選擇適當的懲罰因子C和不敏感因子ε，并選擇適當的核

（3）構造并求解下面的最優化問題：

其中：αi為拉格朗日乘子；由以上最優化問題得到最優解

（4）構造決策函數：

在粒子群算法（Particle Swarm Optimization，PSO）中，每一個優化問題的解都是搜索空間中的一只鳥，稱之為“粒子”。PSO采用速度—位置搜索模型，且所有粒子都有一個根據優化目標定義的適應度值，及一個用于決定它們飛翔方向和距離的速度。

剛開始時，PSO隨機初始化一群粒子，其中第s個粒子在d維解空間的位置和速度分別表示為Xs和通過每一次迭代，粒子動態跟蹤個體極值和全局極值并根據公式（12）和公式（13）實現速度和位置的更新。

文中利用粒子群算法對懲罰因子C值進行優化，其實現步驟包括：①初始化粒子群，包括群體規模N，每個粒子的位置Xs和速度Vs；②計算Z形試驗的運動預報誤差并將其作為每個粒子的適應度；③ 根據粒子的適應度更新Ps和g；④ 根據公式（12）和公式（13）更新粒子群的位置和速度；⑤ 如果達到最大迭代次數或者滿足最小錯誤標準，終止程序；否則，跳轉到步驟②。

2 方法驗證

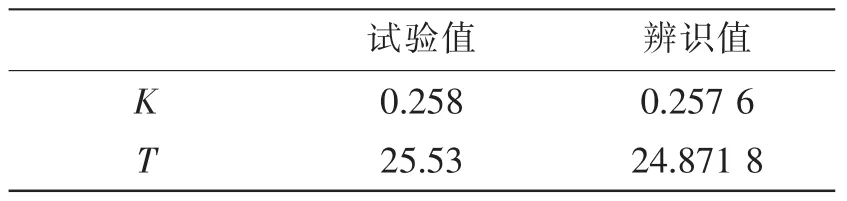
表1 一階線性響應模型操縱性指數結果對比Tab.1 Comparison of manoeuvring indices of the first-order linear response model

圖1 一階線性響應模型10°/10°Z形試驗預報結果和仿真試驗值的比較Fig.1 Prediction results of 10°/10°zig-zag manoeuvre compared with simulated data by using the first-order linear response model

本文首先利用由自航模試驗得到的操縱性指數建立的響應模型[4]進行10°/10°和15°/15°Z形試驗仿真，由仿真試驗得到用于辨識的訓練樣本，其次是設置用于懲罰因子C值尋優的粒子群算法參數，包括：（1）群體規模N。通常，種群太小則不能提供足夠的采樣點，以致算法性能很差；種群太大盡管可以增加優化信息，阻止早熟收斂的發生，但無疑會增加計算量，造成收斂時間太長，表現為收斂速度緩慢。因此，種群規模一般設為100～1 000，文中選擇群體規模N為100；（2）最大迭代次數。迭代次數越多，越能保證解的收斂性，但是影響運算速度，文中選取的最大迭代次數為1 000次；（3）學習因子c1和c2。學習因子分別用于控制粒子指向自身或鄰域最佳位置的運動。通常，c1+c2≤4，文中取c1=c2=2；（4）粒子維數d。粒子維數d取決于待優化的參數個數，而文中待優化的參數只有懲罰因子C值，故文中的粒子維數d為1。

依據文獻[10]和懲罰因子C值的尋優結果，選取C=104和ε=0，在每次辨識時，從每個Z形試驗的數據中選取前100個訓練樣本，運用ε-SVR并采用線性核分別對船舶操縱運動一階線性響應模型和二階線性響應模型進行參數辨識，得到K、T等操縱性指數。然后，用龍格—庫塔法數值求解這些響應模型，進行Z形試驗的運動預報，得到首向角和轉艏角速度預報值。

對于一階線性響應模型，利用10°/10°Z形試驗仿真數據，辨識結果同由自航模試驗得到的操縱性指數“試驗值”的對比見表1。將辨識得到的K、T值代入方程（1），進行Z形試驗的運動預報，得到在一定舵角規律下的首向角和轉艏角速度的預報，其結果和仿真試驗數據的比較如圖1所示。對于二階線性響應模型，利用15°/15°Z形試驗數據，辨識結果同由自航模試驗得到的操縱性指數“試驗值”的對比見表2。將辨識得到的K、T值代入方程（2），進行Z形試驗的運動預報，得到在一定舵角規律下的首向角和轉艏角速度的預報，其結果和仿真試驗數據的比較如圖2所示。

表2 二階線性響應模型操縱性指數結果對比Tab.2 Comparison of manoeuvring indices of the second-order linear response model

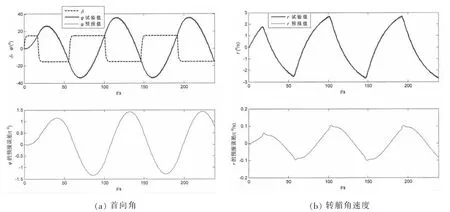
圖2 二階線性響應模型15°/15°Z形試驗預報結果和仿真試驗值的比較Fig.2 Prediction results of 15°/15°zig-zag manoeuvre compared with simulated data by using the second-order linear response model

由上述各圖所顯示的首向角和轉艏角速度預報值同仿真試驗值的比較結果，可以得出以下結論：（1）ε-SVR是一種進行船舶操縱運動響應模型參數辨識的有效方法；（2）粒子群算法是一種有效的懲罰因子C值優化方法，為提高船舶操縱運動響應模型參數辨識精度提供了一個有效途徑。

3 結 論

本文將粒子群算法用于懲罰因子C值的尋優，同時基于Z形試驗仿真數據，應用ε-SVR辨識了船舶操縱運動響應模型參數，并進行了Z形試驗的運動預報。由預報結果同仿真試驗數據的對比結果，可以得出以下結論：（1）ε-SVR是一種進行船舶操縱運動響應模型參數辨識的有效方法；（2）粒子群算法可有效進行懲罰因子C值的優化，為提高船舶操縱運動響應模型參數辨識精度提供了一個有效方法。

[1]Abkowitz M A.Lectures on ship hydrodynamics-steering and manoeuvrability[R].Hydro-and Aerodynamics Laboratory, Report No.Hy-5,Lyngby,Denmark,1964.

[2]Ogawa A,Kasai H.On the mathematical model of manoeuvring motion of ship[J].International Shipbuilding Progress, 1978,25(292):306-319.

[3]Nomoto K,Taguchi T,Honda K,Hirano S.On the steering qualities of ships[J].International Shipbuilding Progress,1957, 4(35):354-370.

[4]賈欣樂,楊鹽生.船舶運動數學模型—機理建模與辨識建模[M].大連:大連海事大學出版社,1999. Jia Xinle,Yang Yansheng.Mathematical model of ship motion-Mechanism modeling and identification modeling[M]. Dalian:Dalian Maritime University Press,1999.

[5]Ebada A,Abdel-Maksoud M.Applying artificial intelligence(A.I.)to predict the limits of ship turning manoeuvres[J]. Jahrbuch der Schiffbautechnischen Gesellschaft,99 Band,2005:132-139.

[6]Moreira L,Guedes S C.Dynamic model of manoeuvrability using recursive neural networks[J].Ocean Engineering,2003, 30(13):1669-1697.

[7]Zhang Xinguang,Zou Zaojian.Estimation of the hydrodynamic coefficients from captive model test results by using support vector machines[J].Ocean Engineering,2013,73:25-31.

[8]Zhang Huaxiang,Cao Linlin,Gao Shuang.A locality correlation preserving support vector machine[J].Pattern Recognition,2014,47(9):3168-3178.

[9]Luo Weilin,Zou Zaojian,Li Tieshan.Application of support vector machine to ship steering[J].Journal of Shanghai Jiaotong University(Science),2009,14(2):462-466.

[10]張心光,鄒早建.支持向量回歸機不敏感因子ε對運動建模的影響[J].中國造船,2011,52(3):46-51. Zhang Xinguang,Zou Zaojian.The effect of SVR insensitive factor on modeling of motion[J].Shipbuilding of China,2011, 52(3):46-51.

Identification of models of ship manoeuvring motion using Support Vector Regression and Particle Swarm Optimization

ZHANG Xin-guang1,ZOU Zao-jian2,3,WANG Yan-song1
(1.Automotive Engineering College,Shanghai University of Engineering Science,Shanghai 201620,China;2.School of Naval Architecture,Ocean and Civil Engineering,Shanghai Jiao Tong University,Shanghai 200240,China;3.State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)

By analyzing the simulated zig-zag test data,Support Vector Regression is applied to conduct mechanism modeling of response models of ship manoeuvring motion.The parameters of response models of ship manoeuvring motion are obtained from the structure of kernel function.The established response models are used to predict zig-zag manoeuvres.To reduce the negative effects produced by choosing randomly the penalty factor C,Particle Swarm Optimization is used to optimize the penalty factor C.The prediction results are compared with the simulated test data to verify the effectiveness of the proposed method.

ship manoeuvring;response model;parameter identification;Support Vector Regression; Particle Swarm Optimization

U661.33

A

10.3969/j.issn.1007-7294.2016.07.009

1007-7294（2016）11-1427-06

2016-08-19

國家自然科學基金項目（51609132）；上海高校青年教師培養資助計劃（ZZGCD15044）；校啟動基金（2015-66）

張心光（1982-），男，講師，通訊作者，E-mail：zxg416@126.com；鄒早建（1956-），男，教授，博士生導師。