“2塊板磚”妙斷“任意”與“存在”難題

?

“2塊板磚”妙斷“任意”與“存在”難題

◇山東齊先昌

高中數學中“任意”與“存在”(“?”與“?”)，出現頻率較高,它常常與“恒成立”“有解”“使……成立”等詞語相呼應．但是由于自身較為抽象,如果碰上一個題目同時研究2個量詞,情況就會變得愈發復雜．因而學生一般遇到此類問題非常頭疼．當然此類問題的求解,在一些報刊上已經研究出不少的成果．但大多數文章,都是對“任意”與“存在”的題型特點以及解題規律進行歸納總結,缺乏更高的認識和普遍適用的較為方便可行的通法．筆者經過長時間的教學實踐的檢驗,最終歸納為“板磚求解法”．這種方法可以輕松應對所有的“任意”與“存在”問題,不需要分門別類一一記憶,可以減輕學生的記憶負擔．

1研究f(x1)與g(x2)的關系等于研究函數f(x)與g(x)的值域集合的關系

在處理“任意”與“存在”的問題中,常見到這樣的條件“f(x1)≥g(x2)”,從等式兩邊不同自變量的取值x1、x2看,它和“f(x)≥g(x)”是有本質區別的,f(x1)與g(x2)只能表示2個函數在給定區間上各自所取的值,也就是該區間上的值域．那么,這里要研究f(x1)與g(x2)的關系,實際上最終都劃歸成2個函數f(x)與g(x)的值域的關系,值域實質就是集合,因此最終是研究2個值域的集合的元素之間的關系,即最大值(元素)、最小值(元素)、普通函數值(元素)．

在平時經常遇到“f(x1)=g(x2)”的情形,在教學實踐中,理解此類問題最大的障礙是2個函數值域的關系,實質上就是集合間的關系判斷．

-2a-2≤g(x2)≤2a-2．

其次,理解值域之間的關系,可以從條件“對于任意的x1∈R,總是有x2∈[-2,2],使得f(x1)=g(x2)成立”的理解入手．最初級的理解為“任意的x1∈R,在x2∈[-2,2]上總是有g(x2)與f(x1)相等”,再進一步地解釋就是:“任意的f(x1),總是有g(x2)與其相等”.更進一步地說:“f(x1)的每一個值,都有一個g(x2)與之對應”.讓數學語言更加通俗,更接近學生的理解水平．

2研究f(x1)與g(x2)所構成的集合就像“2塊板磚”

從前面的案例可見,研究f(x1)、g(x2)的關系僅僅和函數值構成的集合有關系,要想研究f(x1)=g(x2)、f(x1)≥g(x2)、f(x1)≤g(x2)等,只需看集合中的元素的大小、多少,卻與函數f(x)與g(x)的圖象毫無關聯．既然如此,我們再研究此類問題可以毫無顧忌地直接關注函數的值域．在實踐中筆者采用“2塊板磚(長方條)法”代表函數的值域,而板磚的高低長短代表2個集合的包含還是交集關系,這樣可以把完全抽象的最值問題運用具體的圖形來講解演示,形象生動,便于操作,具有舉一反三功效．

2.1板磚法研究f(x1)=g(x2)

“任意+存在”類型:上面案例就是“任意+存在”類型,“任意的x1∈R,在x2∈[-2,2]上總是有g(x2)與f(x1)相等”,用板磚法解釋相當于“2塊板磚”中,因為f(x1)的每一個值,g(x2)都能找到一個和前者對應相等,因此代表f(x1)的板磚短,代表g(x2)的板磚長,位置如圖1所示．

“任意+任意”類型:上面的案例,若對于任意的x1∈R,任意x2∈[-2,2],都有f(x1)=g(x2)成立,用板磚法解釋相當于“2塊板磚”中,因為f(x1)的每一個值與g(x2)的每一個值,相互之間都能找到對應相等的值,因此代表f(x1)的板磚與代表g(x2)的板磚一樣長,位置如圖2所示．

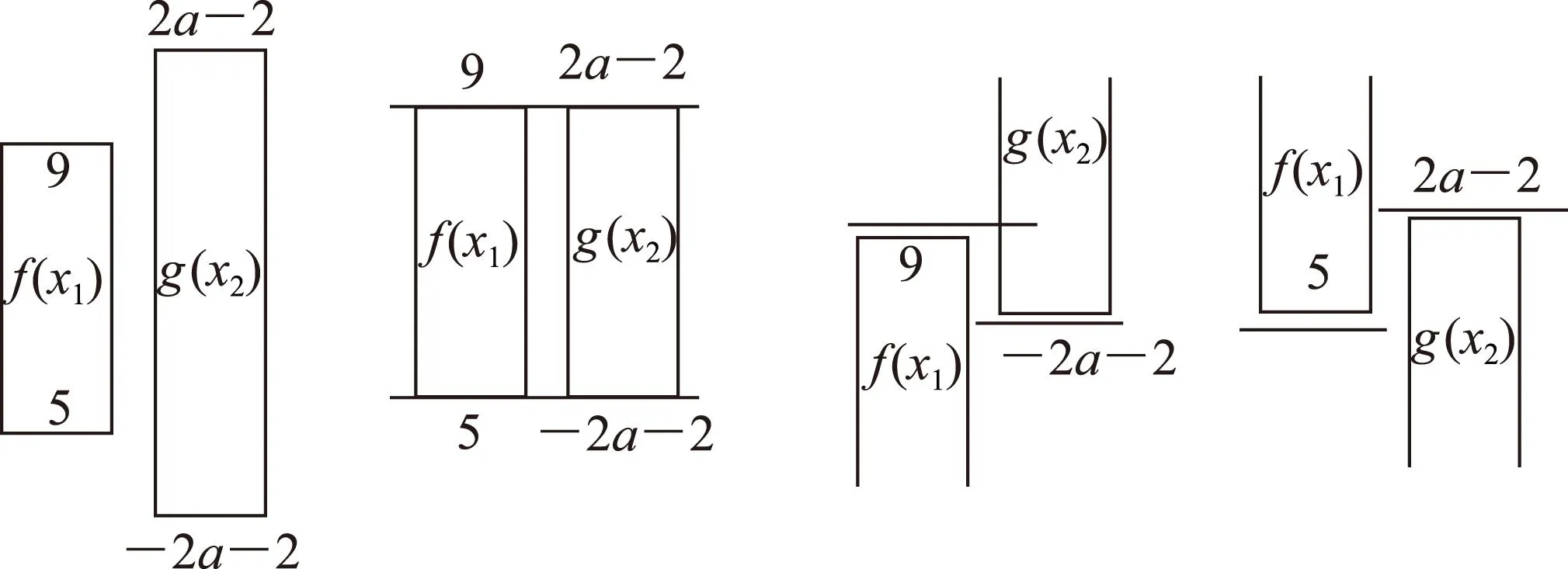
圖1　　　　　圖2　　　　　圖3　　　　　圖4

“存在+存在”類型:上面的案例,若存在x1∈R,存在x2∈[-2,2],使得f(x1)=g(x2)成立,用板磚法解釋相當于“2塊板磚”中,因為f(x1)的至少存在一個值,g(x2)中也至少存在一個值對應相等,這種情況最能顯示板磚的法的優勢．我們可以讓代表g(x2)的板磚上下移動．比如,板磚g(x2)從下向上移動至如圖3時,板磚g(x2)的下沿不能高于板磚f(x1)的上沿,此時雙方均至少存在一個相等的元素(函數值);板磚g(x2)從上向下移動至如圖4時,板磚g(x2)的上沿不能低于板磚f(x1)的下沿,此時雙方均至少存在一個相等的元素(函數值).

2.2板磚法研究f(x1)>g(x2)

“任意+存在”類型:上面案例,“任意的x1∈R,在x2∈[-2,2]上總是有f(x1)>g(x2)”相當于“總有一個g(x2)小于任意的f(x1)”．用板磚法解釋相當于“2塊板磚”中,代表g(x2)的板磚的底沿要低于代表f(x1)的板磚最低沿,位置如圖5所示．

“任意+任意”類型:上面的案例,若對于任意的x1∈R,任意x2∈[-2,2],都有f(x1)>g(x2)成立,用板磚法解釋相當于“2塊板磚”中,代表f(x1)的板磚的下沿總比代表g(x2)的板磚上沿高,位置如圖6所示．

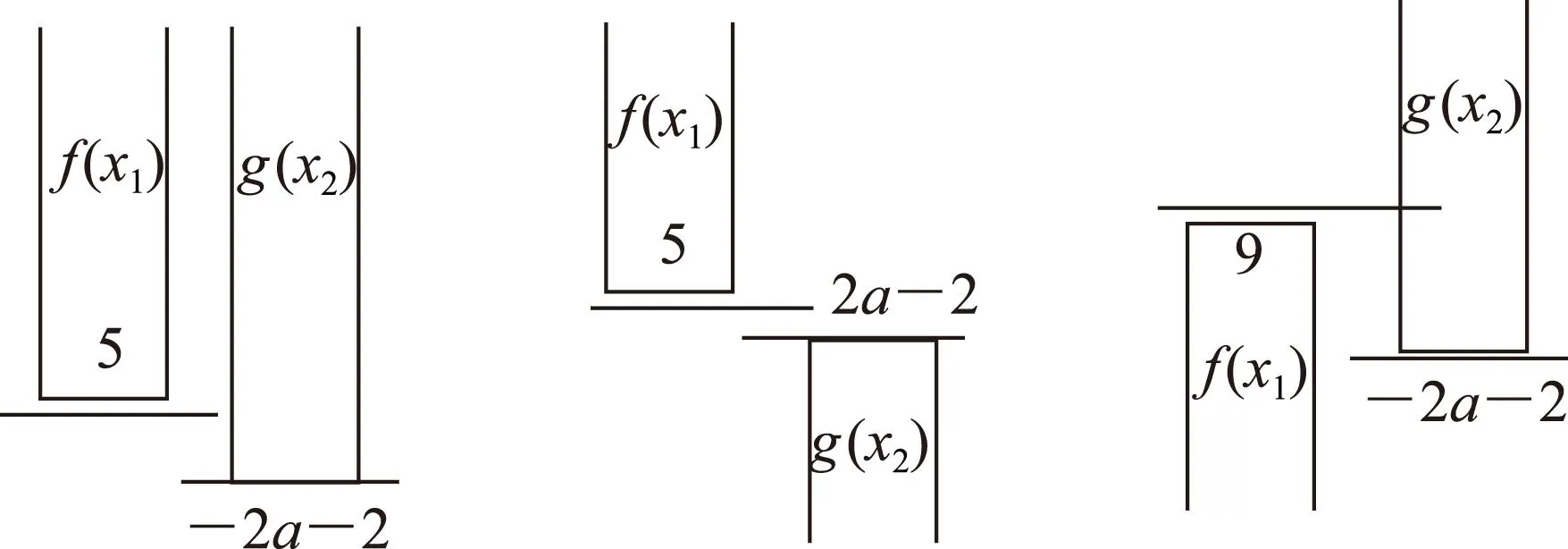
圖5　　　　　　圖6　　　　　　圖7

“存在+存在”類型:上面的案例,若存在x1∈R,存在x2∈[-2,2],使得f(x1)>g(x2)成立,如圖7,用板磚法解釋相當于“2塊板磚”中,板磚g(x2)的下沿不高于板磚f(x1)的上沿．

總之,利用板磚的高低長短,對于上面還沒有涉及到的“任意”“存在”問題類型,也可以同樣的手段非常容易地解決．圖形關系搞清楚之后,再把圖形中反映的2塊板磚的最高點的高低與最低點的高低,轉義成最大值之間與最小值之間的大小關系,形象生動,可操作，簡單易學．上述討論,僅僅為了分別展示板磚對各種情形的適應能力,但是如果我們有了這2塊板磚,在應用中根本不用記住上述各種情形,只需要根據題目條件,適當地移動板磚的上下位置來判斷它們的值域的關系,真是妙不可言．

(作者單位：山東省濟寧學院附屬高中)