淺談數學高考題中定義新符號運算類問題

?

淺談數學高考題中定義新符號運算類問題

◇山東胡文文

定義新符號運算類問題是指題目中給出與高中數學教材里的內容和含義不同的符號及與之有關的運算規則,或給出教材中很少出現的符號及與之有關的運算規則,或給出教材中沒有出現過的具有全新意義的符號及與之有關的運算規則,讓答題者明白符號的內涵和運算法則,并應用所獲得的規則解決問題．

1定義新符號運算類問題的主要特點

1) 創新性. 定義新符號運算類問題的內容圍繞著高中生所學的知識設置,但不拘泥于高中生所學的知識形式和方法,問題的解答過程充分體現高中生思維的創新意識．

2) 靈活應用性. 定義新符號運算類問題的解決方法不局限于常規題型的解法,考查答題者靈活應用所學知識處理問題的能力．

3) 遷移性. 定義新符號運算類問題的解答需要答題者將所學基礎知識和常規方法遷移到新的問題情境中，并進行正確的應用．

2定義新符號運算類問題的一般解法

①S有5個不同的值;

② 若a⊥b,則Smin與|a|無關;

③ 若a∥b,則Smin與|b|無關;

④ 若|b|>4|a|,則Smin>0;

⑤ 若|b|=2|a|,Smin=8|a|2,則〈a,b〉=π/4．

為了更好地做到列舉過程中的不重不漏,可采用如下方式:先寫出2行上下對齊的2個a和3個b,然后保持一行不動,另一行按照一次錯一位的對應,經過5次后即可循環一周,這樣就可以把情況列舉全面,具體過程如圖1～5所示.

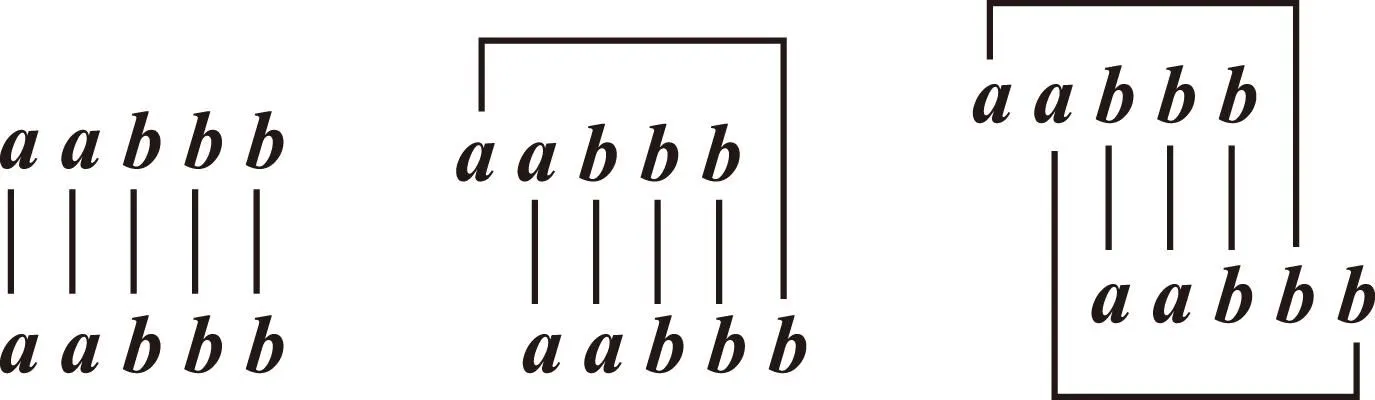
圖1　　　　　圖2　　　　　圖3

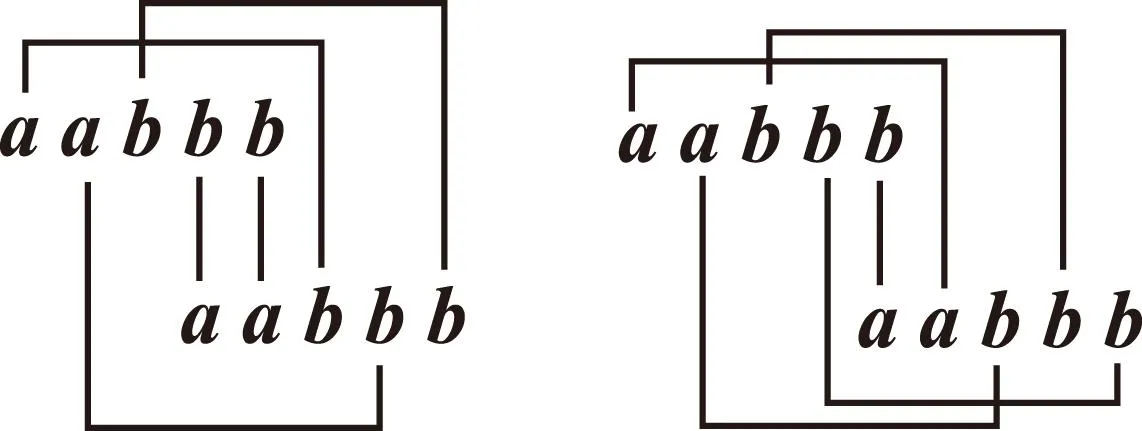
圖4　　　　　　　　圖5

在上述圖中,每個圖的第1行為xi,第2行為yi,上下2行通過中間的黑線進行對應求數量積,然后再將求得的數量積相加即可得到一個S的值．特別注意,在寫數量積的時候,先從短線的對應開始書寫,再寫長線的對應．每個小圖中的S的值的運算過程與結果如下:

圖1中,S=aa+aa+bb+bb+bb=2a2+3b2；

圖2中,S=aa+ba+bb+bb+ab=a2+2ab+2b2；

圖3中,S=ba+ba+bb+ab+ab=4ab+b2；

圖4中,S=ba+ba+ab+ab+bb=4ab+b2；

圖5中,S=ba+aa+ab+bb+bb=a2+2ab+2b2．

綜上所述,S有3個不同的值,即S=2a2+3b2,S=a2+2ab+2b2及S=4ab+b2,故①錯．而②、③、④、⑤的判斷都與Smin有關,選擇作差法對S的所有值進行大小比較,進而求得Smin．由

(2a2+3b2)-(a2+2ab+2b2)=(a-b)2≥0,

(a2+2ab+2b2)-(4ab+b2)=(a-b)2≥0,

可得Smin=4ab+b2．

對②,若a⊥b,則ab=0,所以Smin=b2=|b|2與|a|無關,故②正確.

對③,若a∥b,則存在實數λ,使得a=λb,所以Smin=4ab+b2=(4λ+1)|b|2與|b|有關,故③錯誤.

對④,Smin=4ab+b2=|b|(4|a|cos〈a,b〉+|b|),因為|b|>4|a|,所以

Smin>|b|(4|a|cos〈a,b〉+4|a|)=

4|a||b|(cos〈a,b〉+1)>0,

故④正確.

對⑤,若|b|=2|a|,Smin=8|a|2,則

Smin=4ab+b2=8|a|2cos〈a,b〉+4|a|2=8|a|2,

綜上可得出②、④正確．

解決新定義型問題的一般過程如下:

1) 認真閱讀新定義或新信息的內容,標記關鍵詞,找出新定義或新信息的典型特征;

2) 分析典型特征,弄清新定義或新信息的本質內容;

3) 將新定義或新信息的本質內容與已學過的知識進行聯系;

4) 結合問題確定新定義或新信息使用的數學符號或圖形語言;

5) 選取合適的方法求解問題;

6) 遇到求解不順再補充完善對新定義或新信息的理解;

7) 求解徹底不能進行再從第一步重新開始,充分挖掘已知條件;

8) 結合新定義或新信息檢查結果．

3定義新符號運算類問題的教學建議

為提高高中生解決定義新符號運算類問題的能力,主要是提高學生自學新符號運算的能力,結合教學實際,筆者提出以下幾點教師需要注意的教學建議:

1) 引導學生熟練掌握常用的字母符號等表示的涵義;

2) 引導學生區別相同符號的不同含義;

3) 指導學生規范書寫數學符號語言,防止符號混用;

4) 在分析問題時,指導學生辨識清楚題中符號對應的運算法則,按照給出的法則形式進行思考;

5) 在講解問題時,給學生提供有針對性的變式訓練,主要是涉及相同符號、但運算法則和知識背景不同的題目,防止學生形成思維定勢．

(作者單位：山東省淄博第七中學)