數形結合思想在向中數學中的應用

?

數形結合思想在向中數學中的應用

◇福建丁思敏

數形結合是指在教學過程中,將相關數學知識和圖形結合起來,通過圖形對數學問題進行全面詳細的反映,以便簡化數學問題的分析過程,加強數學教學效果．在高中數學中,數形結合的應用范圍十分廣泛,主要包括方程、不等式、函數等．

數形結合的教學方法具有廣闊的應用前景,其主要有3個方面的優點．

1) 有利于簡化數學概念,便于學生掌握．某些數學概念較為抽象,單靠字面理解很難對其正確認識．通過數形結合,可以讓學生直觀地對相關概念形成認識．

2) 有利于優化解題.在解答相關問題的過程中,結合圖形來觀察其中的關系,對解題具有促進作用,可以提高解題速率、提升解題正確率．

3) 有利于推動數學教學發展．通過數形結合的思想展開教學,可以促進數學教學向更加高效的方向發展．

1在方程、不等式中的應用

對于方程或不等式這類問題而言,數形結合的應用思想就是把相關問題轉化為函數問題,然后根據函數圖象反映出的基本關系進行求解．

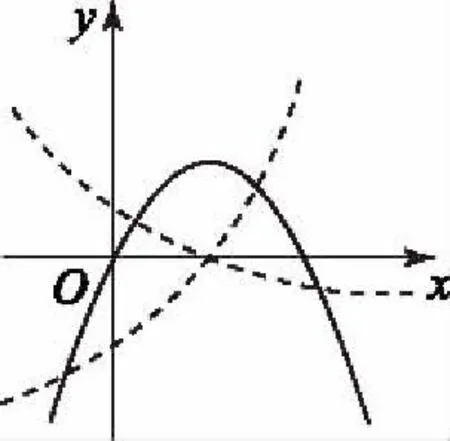
圖1

對于這類只求實根個數的題目,通過圖形判斷是最為簡單的方法．

2在函數中的應用

在函數中應用數形結合教學時,需要明確3個基本點．

1) 深入剖析問題,明確函數圖形．不同的函數，圖形是不一樣的,在解決函數問題時,很多時候都需要對函數進行變形,才能明確其表示的圖形．

2) 畫出函數圖形,根據函數題目中給出的已知條件,畫出準確的函數圖形．

3) 結合圖形對函數問題進行剖析,尋找解題方法．

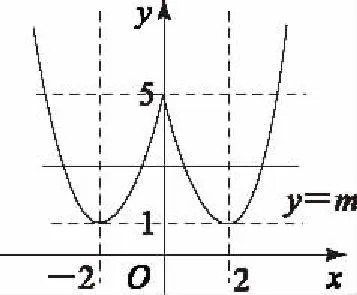
圖2

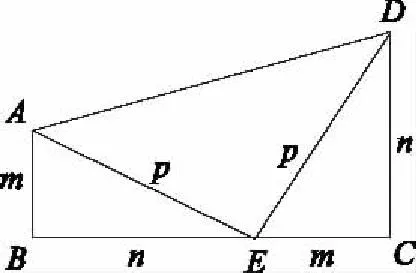
從圖中不難看出,函數有4個零點時,1

3代數式的幾何意義

對于某些代數式而言,其具有一定的幾何意義,通過數形結合思想畫出具體圖形來解題,可以起到顯著的效果．

圖3

綜上，在高中數學教學中,需要加強數形結合思想的運用，明確數形結合思想的解題理念,還需深化數形結合思想的解題應用,促進學生數學水平大幅提升．

(作者單位：福建省龍巖市長汀縣河田中學)