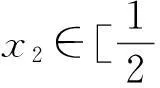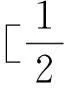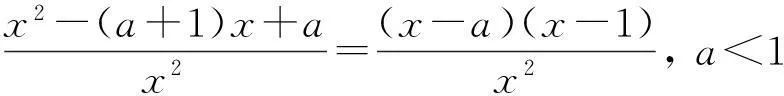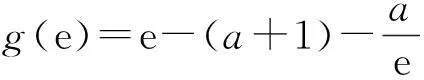聚集含參不等式恒成立問題

?

聚集含參不等式恒成立問題

◇江蘇汪小萍

本文就含參不等式恒成立問題加以歸類解析,以幫助讀者理清常用結論,理解、掌握常用解題思路、方法,不斷提升求解此類問題的實際能力.

1含參一元二次不等式在R上恒成立問題

常用結論:

設二次函數f(x)=ax2+bx+c(a≠0),則

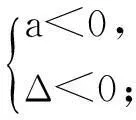
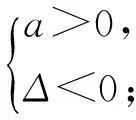
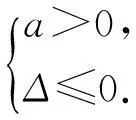
(1) 求a的值;

(2) 若|f(x)-2f(x/2)|≤k恒成立,求k的取值范圍．

分析本題將分段函數及不等式相結合,并對絕對值不等式的應用進行了考查．主要目的在于考查學生分類思想在解題過程中的靈活應用．在第(1)問中,首先需針對a的取值情況進行分析.在第(2)題中,需針對f(x)-2f(x/2)的正負進行分析與討論,從而利用分段函數進行表示,以此為依據求出k的取值范圍．在解題過程中,需要準確掌握絕對值不等式的性質,并靈活運用．

解(1) 由|ax+1|≤3得-4≤ax≤2.又因為f(x)≤3的解集為{x|-2≤x≤1},因此,當a≤0時,不符合題意.

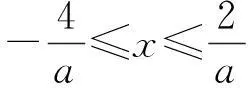
所以|h(x)|≤1,因此k≥1．

2含參不等式在某區間上恒成立問題

常用結論:

a>f(x)恒成立?a>fmax(x);

a≥f(x)恒成立?a≥fmax(x);

a

a≤f(x)恒成立?a≤fmin(x).

解對原函數求導得

3“任意、存在”型不等式恒成立問題

常用結論:

1) 若對任意x1∈D1,總存在x2∈D2,使得f(x1)

2) 若對任意x1∈D1,總存在x2∈D2,使得f(x1)>g(x2)(或f(x1)≥g(x2)),則函數f(x)在D1上的最小值大于(或大于等于)函數g(x)在D2上的最小值.

若對任意x1∈[-1,0],總存在x2∈[e,3],使得f(x1)>g(x2)成立,求實數a的取值范圍.

分析解題關鍵在于,必須明確約束條件“對任意x1∈[-1,0],總存在x2∈[e,3],使得f(x1)>g(x2)成立”,等價于“函數f(x)在[-1,0]上的最小值大于函數g(x)在[e,3]上的最小值”.故需要先求得函數f(x)在[-1,0]上的最小值與函數g(x)在[e,3]上的最小值,然后再運用等價轉化式即可獲解.

解對任意x1∈[-1,0],總存在x2∈[e,3],使得f(x1)>g(x2)成立,等價于函數f(x)在[-1,0]上的最小值大于函數g(x)在[e,3]上的最小值.

當x∈[-1,0]時,f′(x)=x(1-ex)≤0,當且僅當x=0時不等式取等號,f(x)在[-1,0]上單調遞減,f(x)在[-1,0]上的最小值為f(0)=1.

綜上,遇到含參不等式恒成立問題時,我們應結合以上常用結論去考慮問題,以便迅速探求具體的解題思路.

(作者單位：江蘇省揚州市廣陵區紅橋高級中學)