轉(zhuǎn)化法在平面向量中的應(yīng)用

?

轉(zhuǎn)化法在平面向量中的應(yīng)用

◇甘肅郝珍

在高中數(shù)學(xué)教學(xué)和學(xué)習(xí)中涉及多種數(shù)學(xué)思想,轉(zhuǎn)化思想是其中重要的一種.在高三數(shù)學(xué)解題教學(xué)中,應(yīng)以數(shù)學(xué)問(wèn)題為平臺(tái),培養(yǎng)學(xué)生解決問(wèn)題的思想方法,而不是死記硬背一些特殊方法、技巧．經(jīng)常滲透等價(jià)轉(zhuǎn)化思想,可以提高學(xué)生的解題水平和能力．下面以《平面向量的應(yīng)用》為知識(shí)背景,談一下在解題教學(xué)中對(duì)轉(zhuǎn)化思想的滲透．

1利用平面向量基本定理,未知化已知

利用平面向量基本定理,可以把未知向量轉(zhuǎn)化成2個(gè)不共線的已知向量的線性表示．

圖1

2利用平面直角坐標(biāo)系,向量運(yùn)算坐標(biāo)運(yùn)算化

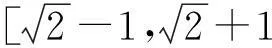
3利用向量的幾何意義,向量運(yùn)算幾何圖形化

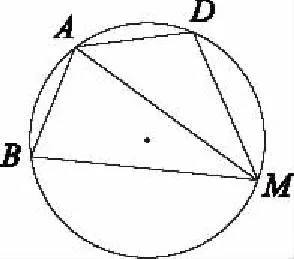
圖2

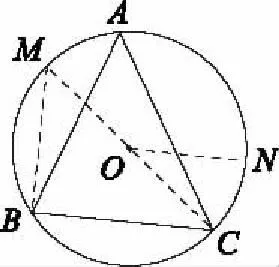
圖3

4利用向量上的投影,任意向量化共線向量

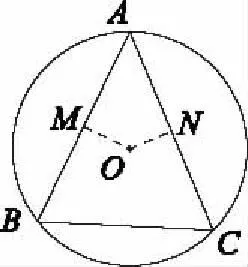
圖4

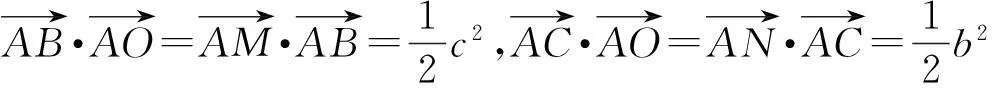
(作者單位：甘肅省嘉峪關(guān)市電大)