如何解決空間幾何體表面上的最值問題

?

如何解決空間幾何體表面上的最值問題

■張永豐

所謂空間幾何體表面上的最值問題，是指空間幾何體表面上的兩點之間的最小距離或某些點到某一個定點的距離之和的最值問題。將空間幾何體表面進行展開是化解該難點的主要方法，對于多面體可以把各個面按照一定的順序展開到一個平面上，將旋轉體(主要是圓柱、圓錐、圓臺)按照某條母線進行側面展開，這樣就把本來不在一個平面上的問題轉化為同一個平面上的問題，結合問題的具體情況在平面上求解最值即可。

例題在長方體ABCD-A1B1C1D1中，AB=3，BC=4，CC1=5，則沿著長方體表面從A到C1的最短路線長為____。

點撥：求幾何體表面上兩點間的最短距離，可以將幾何體的側面展開，利用平面內兩點之間線段最短來解答。

解析：在長方體的表面上從A到C1有三種不同的展開圖。

(1)將平面ADD1A1繞著A1D1折起，得到的平面圖形如圖1所示。

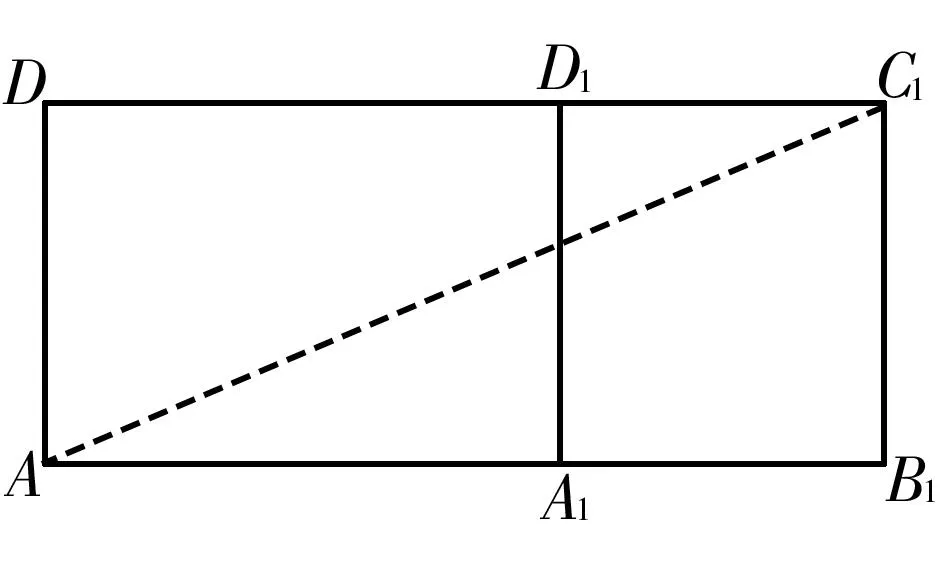
圖1

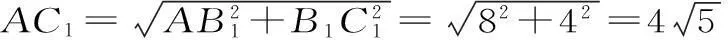
(2)將平面ABB1A1繞著A1B1折起，得到的平面圖形如圖2所示。

(3)將平面ADD1A1繞著DD1折起，得到的平面圖形如圖3所示。

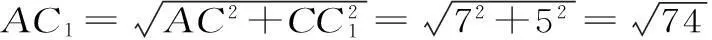
圖2　　　　　　　　　　圖3

點評：本題的難點在于如何將長方體的表面展開，將其表面上的最短距離轉化為平面內兩點間的距離來解決。因為長方體的表面展開圖形狀比較多，其表面展開圖因展開的方式不同，會得到不同的結果，應將這些結果再進行比較才能確定最值。本題易出現的問題是只利用一種表面展開圖得出數據就誤以為是最小值。

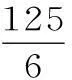
總結：要解決好這類問題，我們同學需要對“空間幾何體的結構特征”、“空間幾何體的三視圖”、“空間幾何體的直觀圖”等知識點非常的熟悉。

作者單位：江蘇省泰興市第一高級中學