考慮懸架影響的汽車操縱穩定性閉環系統Hopf分岔特性*

魏道高, 李莉莉，王 鵬, 蔣亦斌, 潘之杰

(1. 合肥工業大學機械與汽車工程學院，合肥 230009； 2. 浙江吉利汽車研究院有限公司,杭州 310052)

2016023

考慮懸架影響的汽車操縱穩定性閉環系統Hopf分岔特性*

魏道高1, 李莉莉1，王 鵬1, 蔣亦斌1, 潘之杰2

(1. 合肥工業大學機械與汽車工程學院，合肥 230009； 2. 浙江吉利汽車研究院有限公司,杭州 310052)

四輪轉向增加了汽車高速轉向行駛的穩定性，改善了低速時的轉向操縱靈敏性。為了揭示懸置參數對四輪轉向汽車轉向行駛Hopf分岔特性的影響，為某型四輪轉向汽車建立了考慮懸架影響的人-車-路閉環的汽車轉向行駛系統動力學模型和運動微分方程，分析了車輛質心位置和懸架參數對系統分岔特性的影響。結果表明，隨著質心的后移，汽車側向速度、橫擺角速度和車身側傾角的自激振動幅值增大；隨著懸架側傾中心高度的減小，車身側傾角自激振動幅值增大，而側向速度和橫擺角速度的振幅減小；懸架剛度增加能抑制系統發生自激側傾振動。

操縱穩定性；閉環系統；Hopf分岔；極限環

前言

汽車操縱穩定性是其最主要的動力學性能之一，自上世紀30年代人們就開始關注汽車操縱穩定性的研究，目前其線性范圍研究較為成熟[1-3]，非線性動力學分析方法成為熱點，它能夠較全面地反映車輛轉向行駛的本質特性，避免了線性系統只取某一平衡點的鄰域構建車輛行駛動力特性模型的局限性[4-5]。

汽車是多自由度的非線性系統，隨著其行駛速度的提高，車輛轉向行駛的非線性動力學行為變得更加明顯，在工程實際中，顯現出來的一系列問題也更加突出。國內外學者對其展開了深入的研究，取得了一系列成果。主要研究方法分為開環與閉環系統。

文獻[6]中建立了前輪轉向的2自由度汽車轉向行駛平面開環模型，運用分岔理論對其動力學行為進行數值分析，發現隨著車輛行駛速度和前輪轉向角增加系統發生鞍-結分岔；文獻[7]中建立了四輪轉向的2自由度汽車轉向行駛平面開環模型，運用共點軌跡的幾何分析法并結合相平面法對汽車轉向行駛穩定性進行了數值分析，結果表明，在極限工況下，系統除了發生鞍-結分岔，還會發生多種局部、全局分岔和極限環；文獻[8]中考慮車輛縱向速度的變化，建立了3自由度的汽車轉向行駛平面開環模型，對其進行數值分析，發現系統出現混沌運動。

文獻[9]中研究了駕駛員參數對轉向行駛穩定性的影響，提出了駕駛員參數在給定區間內變化時系統是否失穩的判別條件；文獻[10]中建立了閉環系統模型，研究汽車和駕駛員參數對系統平面運動Hopf分岔和極限環數值特性的影響，分析了車速和通向混沌的關系。

綜上研究，由于非線性計算的復雜性的系統模型多局限于平面模型，忽略了車身側傾運動誘發側翻，及側傾運動和平面運動耦合的影響。而考慮車身側傾的文獻又多局限于簧上結構而忽略了懸架參數的影響。因此，本文中考慮懸架構建閉環系統動力學模型，通過定性分析判定系統Hopf分岔存在性和極限環的穩定性與側傾失穩的臨界車速；通過數值計算分析懸架參數和懸置參數對車輛穩定性的影響。

1 系統動力學模型建立

1.1 車輛動力學模型

本文中以某型四輪轉向汽車作為樣車，將其簡化為3自由度力學模型，如圖1所示。圖中，O1為質心，O2為側傾中心。建模時做如下假設：(1)后輪轉向始終與前輪轉向呈正比關系δr=kpδf(δf為前輪轉角，δr為后輪轉角，kp為前后輪轉角比例系數)；(2)忽略懸架與轉向系統結構特點的影響；(3)縱向速度為常量；(4)忽略車輛縱向動力學的影響。

基于以上力學模型和假設，建立該車輛3自由度動力學方程：

2Frcosδr

(1)

(2)

(3)

式中：m為整車質量；v為汽車橫向速度；u為汽車縱向行駛速度；ω為橫擺角速度；ms為簧上質量；Ff為前輪側向力；Fr為后輪側向力；Iz為整車繞橫擺軸(Z)軸的轉動慣量；a為質心到前軸的距離；b為質心到后軸的距離；Ix為整車繞側傾軸(X)軸的轉動慣量；φ為側傾角；cφ為側傾角阻尼；hs為簧上質量質心到側傾軸線的距離，為簧上質量質心高度h與側傾軸線高度hφ的差；kφ為側傾角剛度。

前后懸架側傾角剛度和線剛度的關系為

(4)

式中:ksf和ksr分別為前、后懸架線剛度；B為輪距。取后懸架線剛度為前懸架線剛度的1.5倍，即ksr=1.5ksf=1.5ks，ks為懸架線剛度，則kφ=1.25ksB2。

1.2 駕駛員模型

駕駛員的控制行為是影響閉環汽車操縱穩定性[11-12]的重要因素。目前駕駛員模型主要有補償跟蹤模型[13-14]、預瞄跟蹤模型[15-16]和智能控制模型[17-18]等。簡化的預瞄跟蹤模型因便于仿真分析且精度較高而被廣泛采用。因此本文中選用該模型，其表達式為

(5)

式中:L為駕駛員前方可視距離；Tr為視覺延遲；K為增益放大系數；用(x,y)表示車輛質心O1的水平位置，Ψ為車輛前進方向角，則

(6)

(7)

1.3 輪胎模型

汽車輪胎側向力用魔術公式計算精度較高，但不能進行系統定性分析，而輪胎立方模型[19-20]能進行系統定性分析，該模型與魔術公式計算對比結果如圖2所示。二者較接近，因此，本文中選用輪胎側向力立方模型，對系統穩定性定性分析與數值計算，計算輪胎側向力所需參數如表1所示。

參數數值參數數值C1f(C1r)/(N·rad-1)33020C3f(C3r)/(N·rad-3)481770

輪胎側向力立方模型為

(8)

(9)

其中：

(10)

(11)

式中：C1f，C3f，C1r和C3r為側偏剛度系數；αf和αr分別為前、后輪側偏角。

2 樣車Hopf分岔特性定性分析

汽車操縱穩定性非線性動力學特性分析，主要分為開環和閉環系統兩方面研究，開環系統汽車轉向失穩時主要表現為鞍-結分岔，倍周期和混沌行為。考慮駕駛員的閉環系統在忽略路面激勵的情況下汽車轉向失穩時可能出現Hopf分岔，本文中對第1節建立操縱穩定性閉環自治系統進行Hopf分岔特性分析。尋找樣車發生Hopf分岔的臨界車速和關鍵的車輛性能參數對該分岔的影響。應用文獻[21]判定該系統是否發生Hopf分岔，并尋找速度分岔值，系統參數如表2所示。

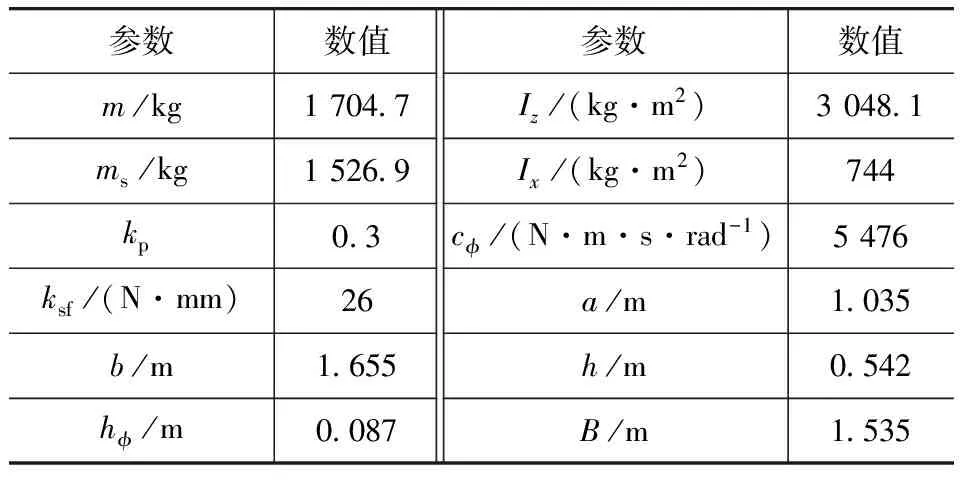
表2 系統參數

2.1 系統Hopf分岔判定

(12)

其中：

令式(12)的特征方程為

(13)

式中：n為矩陣A(u)的特征向量。

根據Hopf代數判據[21-22]，特征方程式(13)有一對純虛根，且其余5個根均具有負實部的充分必要條件為fi(u)>0(i=0,1,…,7)，且Δi>0(i=2,4)，Δ6=0，Δi為式(13)的Hurwitz行列式。

將表2中數據代入式(12)和式(13)，獲得滿足判據條件的含10個不等式和1個等式的方程組：

(14)

計算Jacobi矩陣A(uc)的特征根如表3所示。

表3 矩陣A(uc)的特征根

XL和XR分別為矩陣A(uc)對應特征值4.514670491i的左特征矢量和右特征矢量：

M=

則Jacobi矩陣A(u)的純虛根對應的特征根在uc處關于u的導數n′(uc)=XLMXR=-0.4780389881+0.7406790501i,Re(n′(uc))=-0.4780389881≠0,所以該動力學系統在u=uc處發生Hopf分岔。

2.2 系統Hopf分岔穩定性分析

由上面Hopf分岔代數判別計算可知，該系統在臨界車速工況下，在平衡點發生了Hopf分岔，產生的極限環穩定性根據文獻[22]中Hopf分岔穩定性判據， 令

其中：

式中:iv0為系統在平衡點處的純虛根；O為零矩陣或零向量；i=1,2，…，7。

如果Re(β)>0，則分叉周期解為軌道漸進穩定的；如果Re(β)<0，則分叉周期解為軌道不穩定的。

計算得β=897.1630625+1156.845412i，Re(β)=897.1630625>0，所以系統發生超臨界Hopf分叉，周期解為軌道漸進穩定的，表現為穩定極限環。

3 Hopf分岔特性數值計算與分析

由以上定性分析可知，樣車系統在臨界車速處發生超臨界Hopf分岔，即系統發生蛇行運動。因此，基于以上建立的車輛操縱穩定性系統運動微分方程，運用四階Runge-Kutta法進行數值求解，計算車輛質心與側傾中心參數對系統產生的極限環特性的影響。

3.1 線性模型穩定性計算

為研究樣車穩態行駛時的轉向特性，本文中以車輛四輪轉向時穩態橫擺角速度增益為評價指標進行穩定性分析。將樣車簡化為單軌線性模型，求得其橫擺角速度增益數學表達式為

(15)

其中

(16)

式中:La+b為軸距；K0為穩定性因數；k1和k2分別為前后輪側偏剛度。由表2和式(16)算得K0=0.0036s2/m2。

由表2和式(15)計算得橫擺角速度增益曲線如圖3中實線所示。

由圖3可見，樣車穩態轉向特性具有不足轉向，且該曲線落在美國試驗安全車(ESV)穩態橫擺角速度增益的滿意區域內。

3.2 操穩分岔特性計算

為研究車輛行駛速度對其操縱穩定性能的影響，本文中以車輛前進速度為分岔參數，進行分岔特性分析。得到車輛橫擺角速度ω與車速u的分岔圖，如圖4所示。

由圖4可得，隨著車速u的增大，車輛系統發生了Hopf分岔，其臨界車速為31.5m/s，與第2節定性分析結果接近。在車速u=20～31.5m/s的范圍內，橫擺角速度ω幅值近似為零，車輛行駛狀態趨于穩定，未發生蛇行運動。在車速u=31.5～60m/s的范圍內，車輛橫擺角速度ω幅值先增大后減小，最后趨于穩定，車輛表現為蛇行運動特性。

3.3 質心位置和懸架主要參數的影響

為了研究樣車質心的縱向位置對系統操縱穩定性的影響，取車速u為40m/s時，保持軸距La+b不變，分別改變質心前后位置、懸架側傾中心高度和懸架垂直剛度，計算系統變量響應變化趨勢，計算結果如圖5～圖7和表4所示。

3.4 計算結果與分析

由圖5～圖7和表4可得，保持軸距La+b不變，隨著質心到前軸的距離a的增大、質心到后軸的距離b減小，汽車側向速度v，橫擺角速度ω和車身側傾角φ的自激振動極限環幅值呈增大的趨勢；隨著懸架側傾中心高度hφ的減小，汽車側向速度v和橫擺角速度ω的自激振動極限環幅值呈減小的趨勢，車身側傾角φ的自激振動極限環幅值呈增大的趨勢；隨著懸架線剛度ks的增大，汽車側向速度v和橫擺角速度ω的自激振動極限環幅值有輕微增大的趨勢，車身側傾角φ的自激振動極限環幅值呈減小的趨勢。

參數a=1 035mb=1 655ma=1 085mb=1 605ma=1 135mb=1 555mh?=0 087mh?=-0 013mh?=-0 113mks=26N·mks=36N·mks=46N·mv/(m·s-1)0 760 941 080 760 690 590 820 880 91ω/((°)·s-1)10 1611 6212 510 169 478 5212 2012 2112 23?/(°)2 653 113 372 653 043 253 562 541 95

4 結論

(1)運用Hopf分岔定理判定考慮懸架的人-車-路閉環操縱穩定性系統發生了超臨界Hopf分岔，通過數值計算方法獲取系統分岔的臨界車速為31.6m/s，車輛系統發生了蛇行運動。

(2)隨著懸架側傾中心高度hφ的減小，車身側傾角φ的自激振動極限環幅值呈增大的趨勢，而汽車側向速度v和橫擺角速度ω的自激振動極限環幅值呈減小的趨勢；隨懸架線剛度ks的增大，汽車側向速度v和橫擺角速度ω的自激振動極限環幅值有輕微增大的趨勢，車身側傾角φ的自激振動極限環幅值呈減小的趨勢，而自激振動的頻率基本不變。

(3)今后擬進一步研究懸架參數與懸置參數匹配對系統Hopf分岔和車輛失穩影響。

[1] 郭孔輝. 汽車操縱動力學[M]. 長春：吉林科學技術出版社，1991.

[2]PACEJKAHB.TyreandVehicleDynamics[M].Oxford:Butterworth-Heinemann, 2002.

[3] 魏道高,王子涵,張翼天,等. 轉向系間隙對汽車操縱穩定性影響研究[J]. 汽車工程, 2014, 36(2):139-144.

[4]VINCENTN.VehicleHandling,StabilityandBifurcationAnalysisofNonlinearVehicleModels[D].Maryland:UniversityofMaryland, 2005.

[5] 施樹明，毛振勇，向輝,等. 車輛轉向的穩定性非線性分析方法[J].機械工程學報, 2007, 43(10):77-81.

[6]ONOEiichi,HOSOEShigeyuki,TUANHoangD,etal.BifurcationinVehicleDynamicsandRobustFrontWheelSteeringControl[J].IEEETransactionsonControlSystemTechnology, 1998, 6(3):412-420.

[7]SHENShuiwen,WANGJun,SHIPeng,etal.NonlinearDynamicsandStabilityAnalysisofVehiclePlaneMotions[J].VehicleSystemDynamics, 2007, 45(1):15-35.

[8] 劉麗. 車輛三自由度平面運動穩定性的非線性分析及控制策略評價[D]. 長春：吉林大學，2010.

[9] 趙又群,潘紫微,林棻,等. 駕駛員對汽車行駛方向穩定性影響的分析方法[J]. 中國機械工程, 2006, 17(6):654-655.

[10]LIUZ,PAYREG,BOURASSAE.NonlinearOscillationsandChaoticMotionsinaRoadVehicleSystemwithDriverSteeringControl[J].NonlinearDynamics, 1996, 9:281-304.

[11] 張伯俊. 四輪轉向汽車橫向動力學特性及控制研究[D]. 天津：天津大學, 2006.

[12] 王洪禮,劉晟,遲仲玉. 汽車四輪轉向運動的穩定性分析[J]. 機械強度, 2000, 22(1):23-25.

[13]MCRUERDT.AReviewofQuasi-LinearPilotModels[C].IEEETrans.onHumanFactorsinElectronics, 1967,hfe-8(3):231-249.

[14]HESSRA,MODJTAHEDZADEHA.AControlTheoreticModelofDriverSteeringBehavior[J].ControlSystemsMagazine, 1990, 8:3-8.

[15] 管欣. 駕駛員方向控制模型及閉環駕駛安全性預測方法的研究[D]. 長春：吉林工業大學, 1992.

[16]LEGOUIST,LANEVILLEA,BOURASSAP,etal.CharacterizationofDynamicVehicleStabilityUsingTwoModelsoftheHumanPilotBehaviour[J].VehicleSystemDynamics, 1986, 15:1-18.

[17]MACADAMCC,JOHNSONGE.ApplicationofElementaryNeuralNetworksandPreviewSensorsforRepresentingDriverSteeringControlBehavior[J].VehicleSystemDynamics, 1996, 25:3-30.

[18] 李英. 方向與速度綜合控制駕駛員模型及在ADAMS中的應用[D]. 長春：吉林大學, 2008.

[19]SACHSHK,CHOUCC.OntheStabilityintheSenseofLyapunovofaRubberTireVehicle[J].J.Dyn.Syst.Meas.Control,1976,98(2):180-185.

[20]HUHY,WUZQ.StabilityandHopfBifurcationofFour-Wheel-SteeringVehiclesInvolvingDriver’sDelay[J].NonlinearDynamics, 2000, 22(4):361-374.

[21] 張繼業,楊栩仁,曾京. 分岔的代數判據及其在車輛動力學中的應用[J]. 力學學報, 2000, 32(5):596-605.

[22] 舒仲周,張繼業,曹登慶. 運動穩定性[M]. 北京：中國鐵道出版社, 2001.

Hopf Bifurcation Characteristics of Closed-loop System for Vehicle Handling Stability Considering the Effects of Suspension

Wei Daogao1, Li Lili1, Wang Peng1, Jiang Yibin1& Pan Zhijie2

1.SchoolofMechanicalandAutomotiveEngineering,HefeiUniversityofTechnology,Hefei230009; 2.ZhejiangGeelyAutomobileInstituteCo.,Ltd.,Hangzhou310052

Four-wheel-steering (4WS) system can improve the driving stability of vehicle in high speed cornering and ensure the easy handling of steering in low speed. For revealing the influence of suspension parameters on the Hopf bifurcation characteristics of 4WS vehicle in cornering driving, a driver-vehicle-road closed-loop dynamics model and a set of kinematic differential equations for a 4WS vehicle are established with consideration of the effects of suspension, and the effects of the location of vehicle mass center and the parameters of suspension on Hopf bifurcation characteristics are analyzed. The results show that as the mass center move rearward, the lateral speed and yaw rate of vehicle and the amplitudes of the self-excited roll vibration of vehicle body tend to increase. As the height of suspension roll center reduces, the amplitudes of self-excited roll vibration increase while the vibration amplitudes of lateral speed and yaw rate decrease. The increase of suspension stiffness can restrain self-excited roll vibration.

handling stability； closed-loop system； Hopf bifurcation； limit cycle

*國家自然科學基金(51375130和51050002)資助。

原稿收到日期為2014年4月1日，修改稿收到日期為2014年11月19日。