基于蒙特卡洛的汽車可靠性預測方法研究

楊忠炯,王卉,董棟

(中南大學機電工程學院,湖南長沙 410081)

?

基于蒙特卡洛的汽車可靠性預測方法研究

楊忠炯,王卉,董棟

(中南大學機電工程學院,湖南長沙 410081)

摘要:利用某車型提供的零部件失效數據,擬合其分布類型并進行分布參數估計;通過蒙特卡洛方法,運用MATLAB編程,對整車的平均故障間隔里程進行了預測。分析結果表明,該方法的預測結果與實際情況一致,有較高的可信度,可用于汽車可靠性預測。

關鍵詞:汽車;可靠性;蒙特卡洛;分布擬合;參數估計

汽車可靠性的提高不僅關乎用戶的使用成本和安全性,而且與企業售后服務成本及企業形象有著緊密關系。科學地預測并提高汽車的可靠性已成為國內外汽車企業迫切需要解決的問題。

整車的可靠性指標包括首次故障里程和平均故障間隔里程(時間),零部件的可靠性指標包括失效率、中位壽命等。該文通過零部件的失效分布來計算整車的平均故障間隔里程。由可靠性理論可知,整車由于功能上的關系,構成一個串聯的可靠性模型,整車的可靠性取決于零部件的可靠性。

20世紀60年代以來,蒙特卡洛模擬法在工程領域得到廣泛應用,也有一些學者對蒙特卡洛法用于可靠性分析進行了研究,如:龍東平等運用蒙特卡洛法對機械零件的可靠性進行了研究;周森等將蒙特卡洛法與有限元法相結合,對機械零部件可靠性設計進行了研究;繩鍇等應用蒙特卡洛法對電動汽車車身骨架可靠性進行了研究設計;郝琪和等應用蒙特卡洛法對40 t重型車車架進行了可靠性設計分析;李景魁應用蒙特卡洛法對數控機床液壓系統的可靠性進行了分析;陶元芳等應用蒙特卡洛法對塔式起重機金屬結構的時變可靠性進行了分析;王勝利等應用蒙特卡洛法對共軌噴油器進行了敏感性分析;廖敏輝等應用蒙特卡洛法對液壓系統的可靠性設計進行了研究;B.Echard等應用蒙特卡洛法分析了結構的可靠性。但尚未有學者將蒙特卡洛法運用到整車可靠性分析。該文通過對整車可靠性模型的建立和核心零部件失效概率密度函數的擬合,應用蒙特卡洛法對整車的平均故障間隔里程進行預測,為整車可靠性估計提供一種實用的預測方法。

1 整車可靠性模型及故障數據

整車上零部件有幾百上千個,忽略可靠性較高的次要零部件,將整車看作由發動機、車身、電控系統、底盤結構件、前后懸掛系統、制動系統、轉向系統和冷卻系統等部分組成。整車可靠性屬于串聯模型,只要一個零部件發生故障,則認為整車發生故障。

準確地預測汽車的可靠性,需要知道該車型所使用的零部件及其可靠性數據。根據某汽車企業針對某車型使用壽命的試驗結果統計,所使用部分零部件對應的平均無故障里程如表1所示。

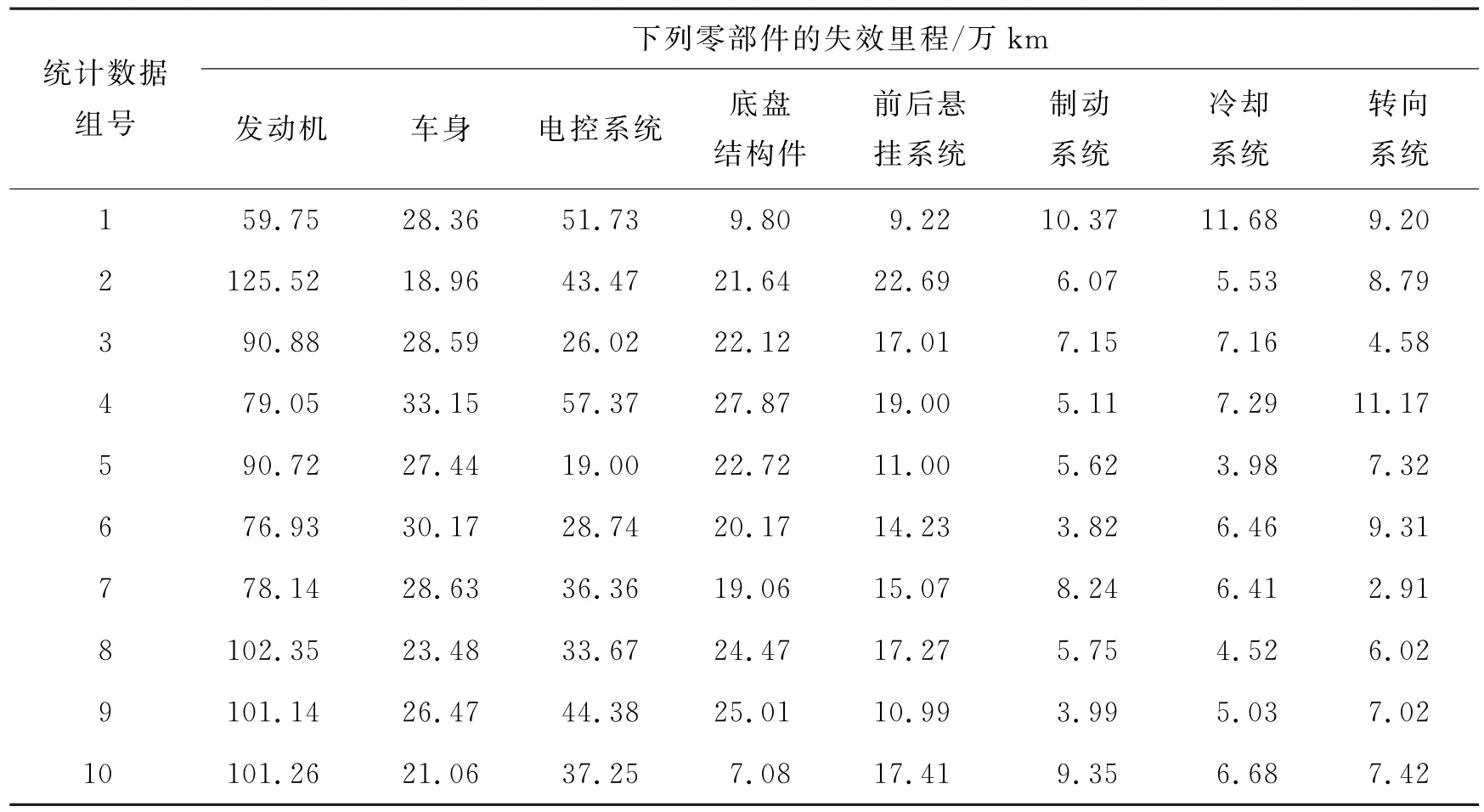
表1 某型汽車部分零部件的失效里程

2 零部件失效概率密度擬合及參數估計

根據表1所示零部件失效數據,可分析得到各零部件失效的分布規律。根據可靠性理論,常見的失效分布形式有指數分布、正態分布和威布爾分布。其中:指數分布是一種數學表達形式最簡單、應用十分廣泛的失效概率密度分布形式,指數分布時的可靠性特征量之間有著極其簡單的關系,它主要有1個特征參數,但指數分布時零部件平均壽命對應的可靠度并不高,只有36.8%。正態分布應用最普通,也最廣,其數學表達式相對復雜,它主要有2個特征參數,正態分布的失效概率密度、失效累積概率、可靠度和失效率也存在相應關系。威布爾分布也是可靠性工程中的基本分布之一,許多零部件的使用壽命都服從這一分布,它有2個特征參數。要確定失效數據所對應的分布類型,首先要知道各種已知分布類型的特點,再把失效的分布規律同已知的標準分布進行比較,從而確定不同零部件失效所服從的分布類型。

將失效數據導入MATLAB,擬合各零部件系統的分布類型(如圖1～8所示),再把擬合所得分布圖形同已知的3種標準分布進行比較。

從圖1～8可以看出:發動機、底盤結構件、制動系統及轉向系統的平均壽命服從指數分布,車身、電控系統及前后懸掛系統的平均壽命服從威布爾分布,冷卻系統的平均壽命服從正態分布。根據各自的分布類型,應用MATLAB,運用極大似然估計對各種分布類型進行置信度為95%的參數估計。

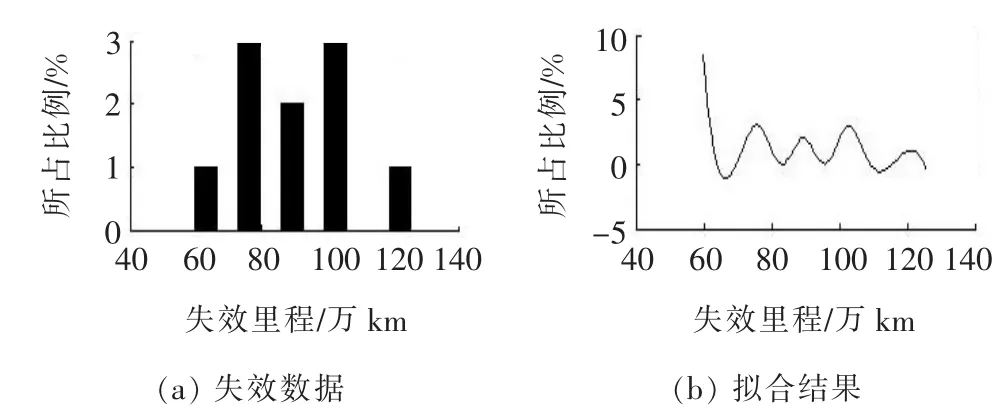
圖1 發動機失效分布類型擬合

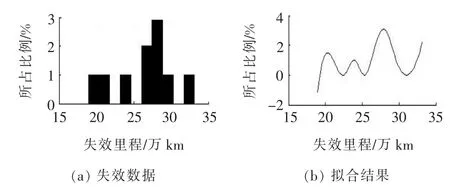
圖2 車身失效分布類型擬合

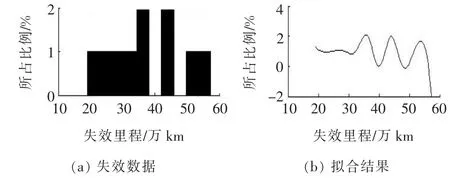
圖3 電控系統失效分布類型擬合

根據各零部件的平均壽命,可得到其分布形式。其中:發動機服從λ=1/(90.6×104)的指數分布;車身服從形狀參數為7.9、尺度參數為28.3的威布爾分布;電控系統服從[41.9,3.8]的威布爾分布;底盤結構件服從λ=1/(20.0×104)的指數分布;前后懸掛系統服從[16.9,4.4]的威布爾分布;制動系統服從λ=1/(6.6×104)的指數分布;冷卻系統服從[6.5,2.1]的正態分布;轉向系統服從λ=1/(7.3 ×104)的指數分布。

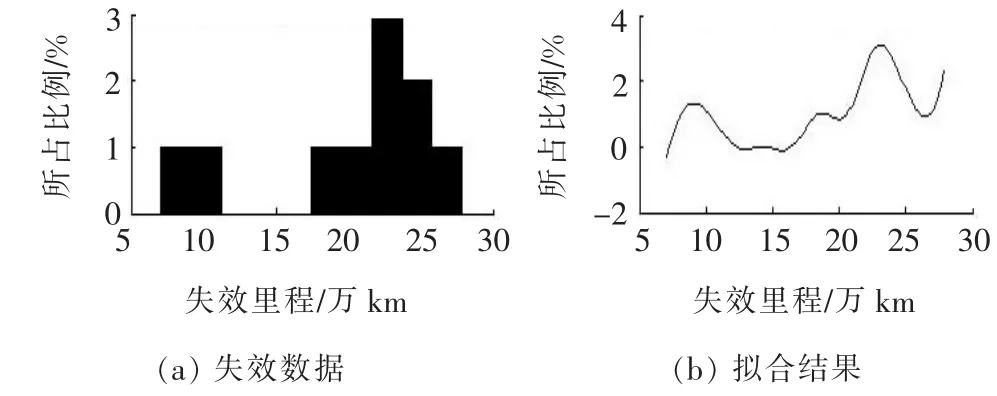
圖4 底盤結構件失效分布類型擬合

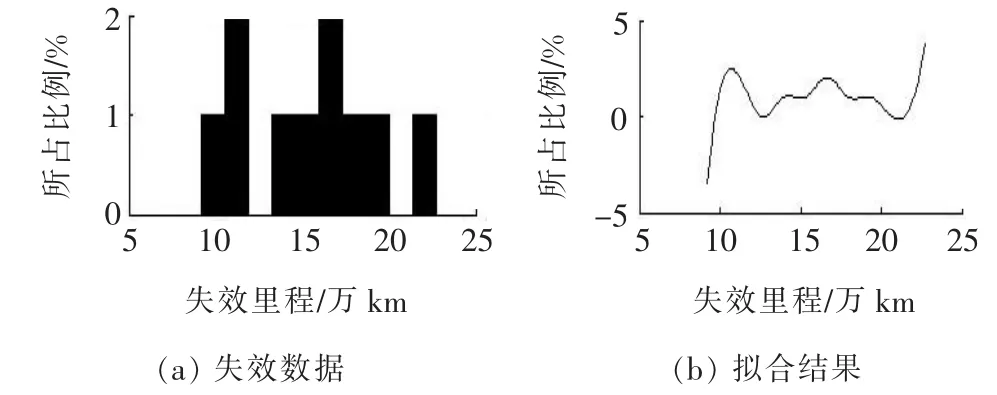
圖5 前后懸掛系統失效分布類型擬合

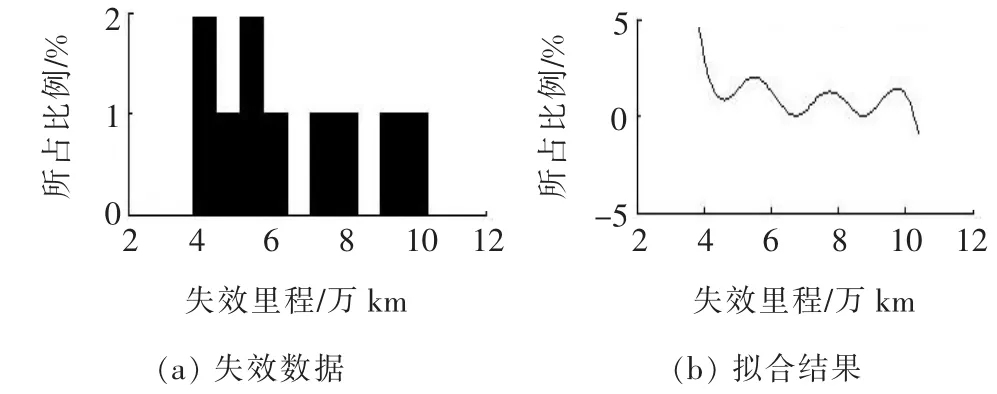
圖6 制動系統失效分布類型擬合

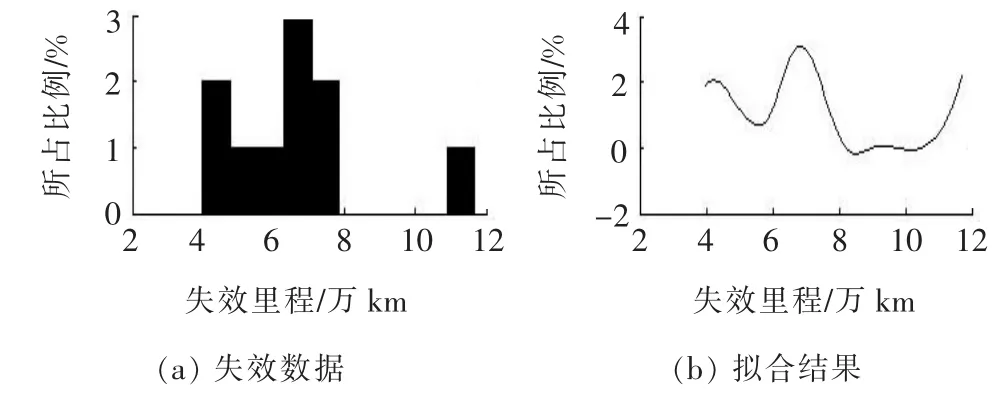
圖7 冷卻系統失效分布類型擬合

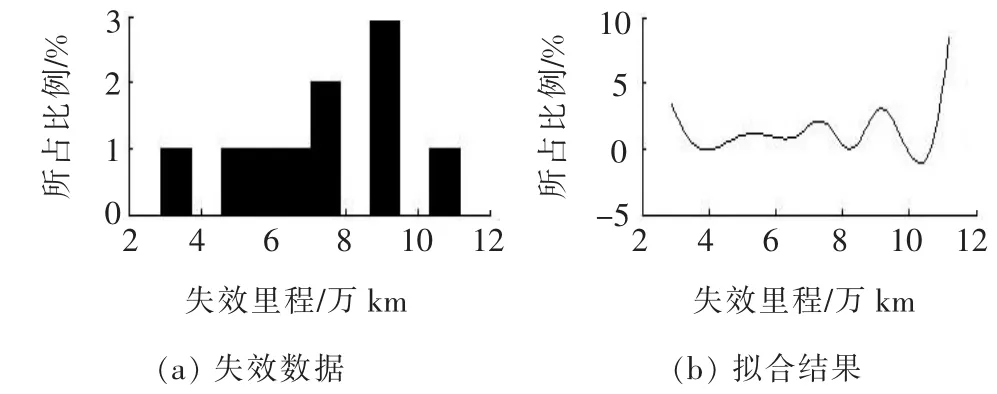
圖8 轉向系統失效分布類型擬合

3 基于蒙特卡羅方法的汽車平均無故障里程計算

平均故障間隔里程(MTBF)為汽車平均無故障行駛的里程,采用規定里程的截尾試驗方法進行統計估算,公式見式(1)。各零部件特征參數估計結果如表2所示。

式中:S為試驗總里程,S=試驗次數×規定的試驗里程;r為全部試驗車輛產生故障的總次數。

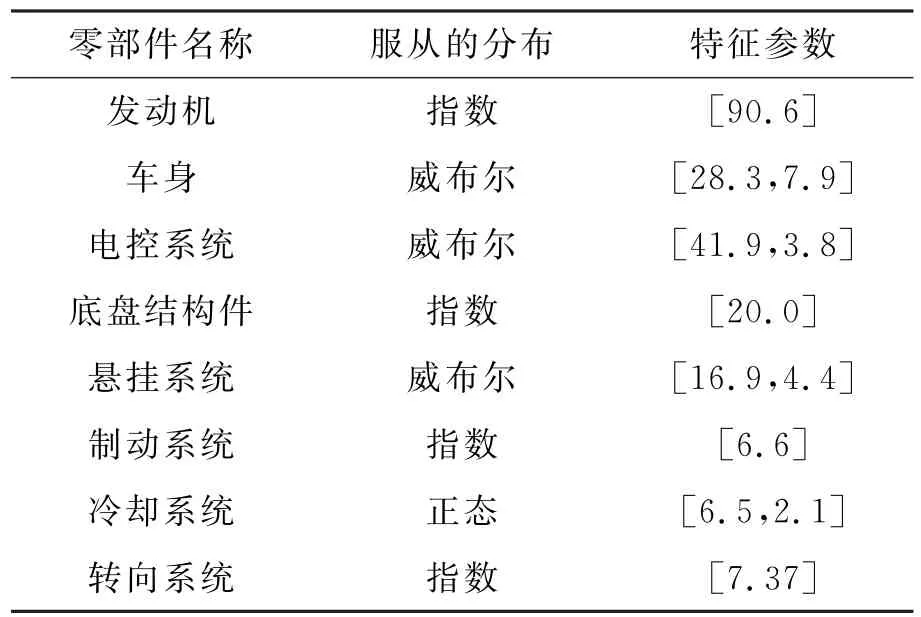
表2 汽車各零部件特征參數估計結果

蒙特卡羅方法根據統計概率函數產生符合統計特征的隨機數,模擬隨機現象,并進行分析預測,其分析預測程序如圖9所示。

首先根據各零部件的分布形式各產生10 000個隨機數,將每個隨機數與期望壽命進行比較,若小于期望壽命,則認為失效。運用上述方法和參數進行仿真,得到每個零部件的失效個數及部分特征參數(如表3所示)。

根據表3,失效事件數為:

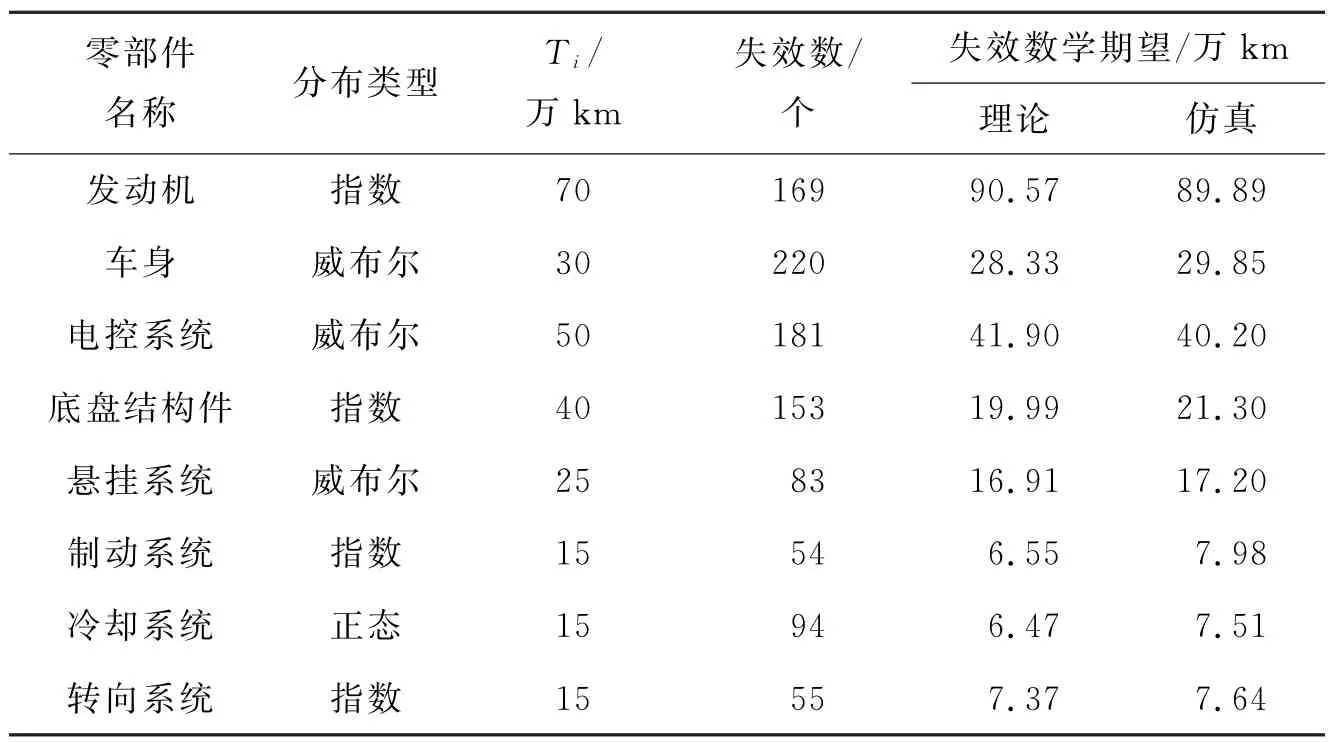
表3 蒙特卡羅仿真結果

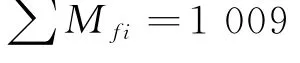
平均首次故障里程為:

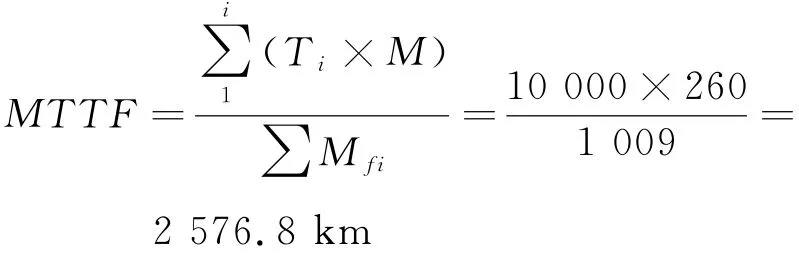
由表3可知:仿真次數為10 000次,對于失效事件的數學期望,理論值和仿真結果統計值非常接近,基本符合實際情況。

4 結語

該文根據某型汽車現有失效數據,擬合出其所服從的分布類型,并通過參數估計得出對應分布的特征參數值。根據蒙特卡羅方法,利用MATLAB產生隨機數并進行統計計算,得到該車型的平均無故障里程。

對平均無故障里程的準確預測有助于制訂合理的汽車可靠性改善方案,并對其保修里程的設定有很大參考價值,可極大地節省汽車生產企業的生產和售后成本。

參考文獻:

[1]鹿應榮.國產汽車的整車可靠性評價[J].汽車工程,2001,23(2).

[2]宋年秀,陳立輝,付文光.CA6400UA型輕型客車整車可靠性研究[J].農業機械學報,2003,34(5).

[3]胡雪海.城市客車可靠性設計[J].客車技術與研究,2008(5).

[4]胡可釗.對我國客車可靠性、安全性及環保的一些認識[J].客車技術與研究,2001(4).

[5]龍東平,馮進,張慢來,等.蒙特卡洛法在機械零件可靠性設計中的應用[J].石油機械,2004,32(4).

[6]周森,張曉毅,何曉聰,等.機械零部件可靠性設計方法研究[J].新技術新工藝,2013(12).

[7]繩鍇,楊坤,吳靜,等.基于可靠性的電動汽車車身骨架設計分析[J].湖北汽車工業學院學報,2015,29(3).

[8]郝琪,呂鵬,汪波,等.基于可靠性的40 t重型車車架設計分析[J].機械設計與制造,2015(6).

[9]李景魁.基于蒙特卡羅法數控機床液壓系統可靠性分析[J].液壓與氣動,2011(11).

[10]陶元芳,劉曉光,邵南曦,等.塔式起重機金屬結構的時變可靠性分析[J].起重運輸機械,2015(9).

[11]王勝利,夏興蘭,陳大陸,等.應用蒙特卡洛方法對共軌噴油器進行敏感性分析[J].現代車用動力,2014(2).

[12]廖敏輝,柴光遠.蒙特卡洛模擬法在液壓系統可靠性設計中的應用[J].機床與液壓,2013,41(11).

[13]B Echard,N Gayton,M Lemaire.AK-MCS:an active learning reliability method combining Kriging and Monte Carlo Simulation[J].Structural Safety,2011,33(2).

收稿日期:2016-01-09

中圖分類號:U461.7

文獻標志碼:A

文章編號:1671-2668(2016)02-0015-04