基于DP優化的ISG型速度耦合混合動力汽車模糊控制策略的研究*
楊亞聯,葉 盼,胡曉松,蒲 斌,洪 亮,張 喀
(1.重慶大學,機械傳動國家重點實驗室,重慶 400044; 2.北京理工大學機械與車輛學院,北京 100081)
2016108
基于DP優化的ISG型速度耦合混合動力汽車模糊控制策略的研究*
楊亞聯1,葉 盼1,胡曉松2,蒲 斌1,洪 亮1,張 喀1
(1.重慶大學,機械傳動國家重點實驗室,重慶 400044; 2.北京理工大學機械與車輛學院,北京 100081)
為增進混合動力汽車中模糊控制能量管理策略設計的合理性,運用動態規劃算法,對ISG型速度耦合混合動力汽車進行性能全局優化,通過分析動態規劃算法的控制結果,提取設計參數,擬定模糊控制規則和模糊控制策略,設計了相應的模糊控制器。建立基于Matlab/Simulink仿真模型,對動態規劃算法和模糊控制策略的仿真結果進行對比,結果表明,所設計的模糊控制策略達到了預期的效果,采用的方法合理有效。
混合動力汽車;模糊控制;動態規劃;ISG
前言
隨著人類社會發展對可持續的節能、環保需求逐漸提高,清潔能源汽車中混合動力汽車由于具有良好的性價比,在產品開發中得到了日益廣泛的關注。混合動力汽車傳動系統中有多個動力源,整車性能的提升有賴于對動力源中能量流的有效管理。
目前混合動力汽車能量管理策略主要包括基于邏輯或規則的控制策略、瞬時優化控制策略和全局最優控制策略。其中,基于邏輯規則的控制策略包括基于邏輯門限控制策略、模糊控制策略和神經網絡等控制策略[1]。基于邏輯規則的控制器可實施性強,其中模糊控制策略易于實現非線性控制,魯棒性好,得到了廣泛的應用[2-4],但模糊控制規則的制定需要專家經驗和對系統的大量深入分析或實驗,規則的擬定也缺乏一種系統的設計指導方法;瞬時優化控制策略雖然能得到接近優化的控制性能,但控制復雜,計算量大[5-6];全局最優控制策略雖然能得到混合動力系統的最優性能,但必須預知行駛循環[7-9]。因此局限了瞬時優化和全局最優控制策略的實際應用,但通過對全局最優控制策略仿真結果的分析有助于混合動力系統能量管理策略的設計[10-11]。
本文中采用動態規劃算法對ISG型速度耦合混合動力系統的性能進行優化,并通過分析動態規劃算法的仿真結果,提取設計參數,擬定模糊控制規則和模糊控制策略,為ISG速度耦合混合動力傳動模糊控制器的設計提出了一種有效的方法。
1 模糊控制策略設計思路
1.1 混合動力系統結構
一種ISG速度耦合混合動力傳動系統的結構如圖1所示。系統中采用行星排進行動力的速度耦合,其中發動機接齒圈,ISG電機接太陽輪,通過行星架輸出動力,在電機和發動機之間,布置有單向離合器和濕式多片離合器。
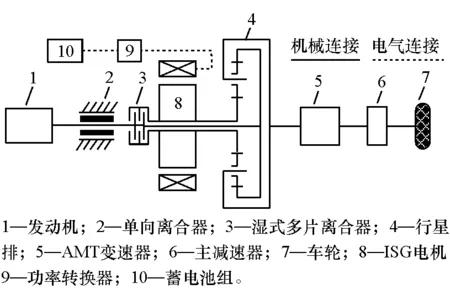
圖1 ISG型速度耦合混合動力系統結構圖
該混合動力系統的運行模式主要包括純電動、行車充電、發動機單獨驅動、行車助力和再生制動等5種模式。當系統在純電動驅動時,由于單向離合器鎖止了發動機的反轉,電機通過太陽輪傳遞動力,由行星架輸出,在制動過程中,通過行星齒輪機構回收制動能量,并能不受發動機反拖轉矩的影響,提升了系統能量回收率。在混合動力驅動模式中,當離合器脫開時,電機可以通過行星輪系調整發動機的工作點,當離合器接合時,發動機和電機固接成整體,系統變換成為并聯型常規ISG混合動力傳動。因此,該系統在保持ISG混合動力系統特點的基礎上進一步提升了其性能。
1.2 控制系統框架結構
本文中采用了便于工程應用的模糊控制策略,其原理結構如圖2所示。

圖2 速度耦合混合動力系統模糊控制框架
為獲得良好的整車燃油經濟性,需要在滿足汽車行駛功率和需求轉矩的情況下,合理地分配發動機和電機的轉矩。為此,如圖2所示,系統通過參數插值求取發動機的最佳轉矩,并將車速、加速度、電池SOC等信號輸入模糊控制器得到發動機轉矩分配系數k,當前條件下的發動機最佳轉矩和分配系數k的乘積即為發動機所分配的轉矩,而電機轉矩分配計算需要考慮濕式多片離合器接合和斷開兩種情況:
(1) 濕式多片離合器接合的情況下系統為常規ISG混合動力系統。
Tm=Tc-Te
(1)
(2) 濕式多片離合器分離的情況下,可以建立單排行星齒輪機構特性方程式[12]:
ωm+αωe-(1+α)ωc=0
(2)
同時,根據功率平衡,可以得出電機的轉矩為
Tm=(pc-pe)/ωm
(3)
式中:Te,Tm和Tc分別為發動機、電機和行星架輸出端的轉矩;ωe,ωm和ωc分別為發動機、電機和行星架輸出端的轉速;pe和pc分別為發動機、行星架輸出端的功率;α為齒圈與太陽輪齒數比。
2 動態規劃算法
2.1 最優問題闡述
利用動態規劃原理,為了獲取在一定循環狀況下混合動力系統的優化能量管理策略,將已知循環工況劃分為N個階段(即網格化),對于每一步長都對應一個狀態,并計算狀態轉換過程中的油耗Jk,通過多階段的決策,實現設定循環工況下油耗最低,該過程可由如下尋優目標函數模型來表示:
x(k+1)=f(x(k),u(k))
(4)
Jk=fuel(k)
(5)
(6)
式中:x(k)為表征車輛運行狀態的狀態變量,如當前的發動機轉速ωe、電池荷電狀態SOC(k)等;u(k)為控制變量,如發動機的油門開度Theta(k)和電機轉矩Tm(k)等;Jk為狀態轉移過程中發動機的燃油消耗量;fuel(k)是與第k階段有關的油耗函數。動態規劃算法要解決的就是在滿足一定的約束條件下,求解目標函數的極值。
本混合動力系統中應滿足的約束條件為
(7)
式中:下標min和max分別表示變量的最小和最大值。
2.2 附加代價函數
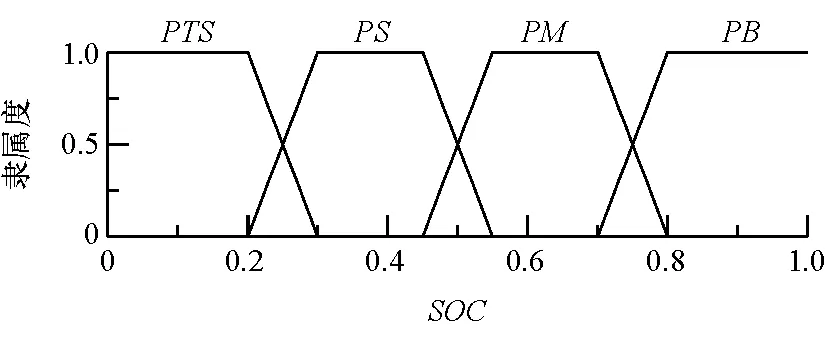
在全局尋優的過程中,須考慮狀態變量的一個合理選擇,仿真過程中,須考慮電池荷電狀態SOC值處于合適的區間。為此,在目標函數中加入SOC值的懲罰項。
Lb(k)=β(SOC(k)-SOCdes)2
(8)
式中:β為電池SOC懲罰系數;SOCdes為目標SOC值。
另外,在混合動力汽車實際運行中,若直接用上述目標函數求解,可能會出現汽車短時間內頻繁換擋的不合理現象。為此加入換擋懲罰項以限制頻繁換擋。
Lg(k)=γ|g(k+1)-g(k)|
(9)
式中:γ為換擋懲罰值;g(k)為AMT變速器擋位。
2.3 目標函數建立
在初始目標函數中,加入代價函數,并結合貝爾曼最優化原理[13],目標函數可以描述為如下方程:
L(x(k),u(k))=fuel(k)+Lb(k)+Lg(k)
(10)
對于第N階段:
JN(x(N))=0
(11)
故對于第N-1階段:
(12)
對于第k階段,其中0≤k (13) 此時,在約束條件下求解上述目標函數最小時系統的油耗和相應的控制變量,即求對應各階段混合動力系統的能量管理策略。 2.4 動態規劃算法仿真結果 表1為ISG型速度耦合混合動力汽車的運行參數。 表1 混合動力汽車運行參數 圖3 UDDS工況仿真結果圖 結合圖1所示的ISG型速度耦合混合動力系統結構與上述的DP優化算法,基于Matlab/Simulink建立了系統仿真模型,選取道路循環UDDS工況進行仿真,得到了如圖3所示的仿真結果。 仿真結束時,電池SOC恢復到仿真開始時的水平,混合動力汽車的百公里油耗為5.312 9L。 3.1 設計參數提煉 能量管理模糊控制策略主要設計參數[14]如表2所示。 表2 模糊控制策略所需主要參數表 Pemax,SOCmin,SOCmax和SOCopt等可以根據發動機和電池的性能試驗等來確定,其中Pemax=72kW,SOCmin=0.2,SOCmax=0.8,SOCopt則是SOC為0.55~0.7之間的區域,此時電池的充放電效率較高。取SOC初始值0.6。 3.2 輸入輸出隸屬度函數的建立 圖4 汽車運行模式與速度、加速度關系 根據DP算法在UDDS與NEDC工況下的仿真結果,可以得到如圖4所示的汽車運行模式與速度、加速度關系。在制定模糊控制策略時,根據圖4來制定輸入變量的隸屬度函數等,有助于使混合動力系統在實際控制過程中按照類似于DP算法仿真下的運行狀態運行,以提高整車的燃油經濟性。 根據圖4,可以得出該混合動力系統純電動模式的汽車車速上限vev大致為50km/h,純電動模式的加速度上限aevmax大致為0.7m/s2。純電動模式的加速度一般規律如圖4中的模式界限曲線。 由此,建立模糊控制策略輸入變量車速和加速度的隸屬度函數,在此隸屬度函數選取梯形函數。車速的模糊子集定義為{PTS,PS,PM,PB,PTB};加速度的模糊子集定義為{PMS,PTS,PS,PM,PB,PTB}。論域則根據循環工況中最大車速與最大加速度設置。具體的隸屬度函數如圖5和圖6所示。 圖5 車速隸屬度函數 圖6 加速度隸屬度函數 電池SOC隸屬度函數如圖7所示,定義其模糊子集為{PTS,PS,PM,PB},論域為[0,1]。 圖7 電池SOC隸屬度函數 圖8為混合動力汽車在DP算法仿真時發動機工作點分布。由圖可知,在混合動力系統運行過程中,發動機絕大部分工作點分布在發動機最佳燃油經濟性曲線附近,設k值表示發動機工作點轉矩相對相同轉速最佳燃油經濟性曲線上轉矩的比值,則DP優化控制策略中發動機的工作點大致在k值為[0.88,1.06]的范圍內。考慮到模糊控制策略的特點,將范圍適度放寬,定為[0.85,1.1]。 圖8 DP算法下發動機工作點 同時,根據對DP運算結果的分析得出:當加速度較大時,發動機會以更大的功率輸出以滿足驅動汽車的要求;當車速較高而加速度不大時,發動機傾向于降低輸出功率以達到油耗與效率的平衡。故此處將[0.85,1.1]劃分為3個區域。考慮到當電池SOC過高時,須使電池放電;當汽車需求功率過大時,須使發動機提供更大的功率。故建立如圖9所示輸出變量k的隸屬度函數,其模糊子集定義為{O,PS1,PS2,PS3,PM1,PM2,PM3,PB},論域為[0,1.5]。 圖9 輸出變量隸屬度函數 3.3 模糊控制規則 為避免過分依賴人的經驗,以DP算法的運算結果為基礎,根據發動機、電機在汽車運行過程的工作規律,得出模糊控制規則,如下所示。 其中,規則①表示汽車的運行狀態處于純電動工作模式的論域內,汽車以純電動模式運行;規則②與規則①的區別在于電池的SOC過低,汽車以行車充電模式運行;規則③表示電池SOC較低,不滿足純電動運行條件,汽車以行車充電模式運行;規則④表示電池SOC適中,為避免電池過充,適當降低發動機輸出;規則⑤和規則⑥表示電池SOC過高而又不滿足純電動運行模式,降低發動機輸出,迫使電池放電;規則⑦表示汽車當前以行車助力模式運行。 3.4 模糊控制策略結果分析 采用上述的模糊控制器,在UDDS循環工況下對上述ISG速度耦合混合動力系統性能進行了仿真,結果如圖10所示。 圖10 UDDS循環工況下仿真結果 仿真結束時電池SOC為0.529,整個循環過程,電池SOC維持在理想的工作區間;混合動力汽車在該循環工況下的等效100km油耗為5.615 4L,對比動態規劃算法的結果,相差5.69%。 為驗證模糊控制策略在其他循環下的控制效果,選取與《GB/T 19233—2008輕型汽車燃料消耗量試驗方法》所采用的循環工況一致的NEDC循環進行仿真,結果如圖11所示。 圖11 模糊控制策略仿真結果 仿真結束時電池SOC為0.663 1,整個循環過程,電池SOC也維持在理想的工作區間;混合動力汽車在該循環工況下的等效100km油耗為5.725 7L,而采用DP優化后的等效100km油耗為5.509 2L,常規車的實測油耗為8.53L/100km,數據對比如表3所示。說明對不同控制循環同樣取得了良好的效果。 表3 NEDC循環工況下仿真結果對比 通過表3的數據對比,表明所設計的模糊控制策略有良好的實際效果。 (1) 本文中采用動態規劃的方法,將ISG速度耦合混合動力系統的全局優化問題轉變為多階段的決策問題。 (2) 基于DP優化的結果,在不同車速和加速度下純電動工況點分析,建立了純電動工況的論域;對不同工況下DP優化控制時發動機萬有特性上工作點的分布,建立了發動機的最佳驅動轉矩論域,并設計了相應變量的模糊隸屬度函數和模糊控制規則,設計了模糊控制器。 (3) 通過在UDDS和NEDC工況下模糊控制器的性能仿真,UDDS下油耗為5.615 4L/100km,相對DP全局優化結果相差5.69%,在NEDC工況下,系統采用模糊控制,燃油消耗為5.725 7L/100km,相對于DP運算結果,相差3.93%;相對常規車,油耗減少了32.8%,說明了控制的適用性和有效性。 [1] 舒紅.并聯型混合動力汽車能量管理策略研究[D].重慶:重慶大學,2008. [2] SCHOUTENA N J, SALMAN M A, KHEIR N A. Energy management strategies for parallel hybrid vehicles using fuzzy logic[J]. Control Engineering Practice,2003,11(2):171-177. [3] LI S G, SHARKH S M, WALSH F C, et al. Energy and battery management of a plug-in series hybrid electric vehicle using fuzzy logic[J]. IEEE Transactions on Vehicular Technology,2011,60(8):3571-3585. [5] 王鋒,冒曉建,卓斌.ISG并聯混合動力轎車最優轉矩分配策略[J].重慶大學學報,2008,31(5):499-504. [6] LIU J, PENG H. Modeling and control of a power-split hybrid vehicle[J]. IEEE Transactions on Control Systems Technology,2008,16(6):1242-1251. [7] PéREZ L, BOSSIO G, MONITRE D, et al. Optimization of power management in an hybrid electric vehicle using dynamic programming[J]. Mathematics and Computers in Simulation,2006,73(1):244-254. [8] JOHANNESSON L, ?SBOG?RD M, BO E. Assessing the potential of predictive control for hybrid vehicle powertrains using stochastic dynamic programming[J]. IEEE Transactions on Intelligent Transportation Systems,2007,8(1):71-83. [9] LIU J, PENG H. Integrated thermal and energy management of plug-in hybrid electric vehicles[J]. Journal of Power Sources,2012,216(15):237-248. [10] LIU Jinming. Modeling configuration and control optimization of power-split hybrid vehicles[D]. USA: The University of Michigan,2007. [11] LIN C, PENG H, GRIZZLE J W, et al. Power management strategy for a parallel hybrid electric truck[J]. IEEE Transactions on Control Systems Technology,2003,11(6):839-849. [12] 陳家瑞.汽車構造[M].北京:人民交通出版社,2006. [13] BERTSEKAS D P. Dynamic programming and optimal control[M]. USA: Athena Scientific,2005. [14] 于永濤.混聯式混合動力車輛優化設計與控制[D].長春:吉林大學,2010. A Research on the Fuzzy Control Strategy for a Speed-coupling ISG HEVBased on Dynamic Programming Optimization Yang Yalian1, Ye Pan1, Hu Xiaosong2, Pu Bin1, Hong Liang1& Zhang Ka1 1.ChongqingUniversity,StateKeyLaboratoryofMechanicalTransmission,Chongqing400044; 2.SchoolofMechanicalEngineering,BeijingInstituteofTechnology,Beijing100081 In order to improve the design rationality of fuzzy energy management strategy for a hybrid electric vehicle (HEV), dynamic programming (DP) algorithm is used for a global optimization on the performance of a speed coupling ISG HEV. Then by analyzing the control results of DP algorithm with design parameters extracted, the rule and strategy of fuzzy control are worked out and a corresponding fuzzy controller is designed. Finally a simulation model is set up based on Matlab/Simulink, and the simulation results with DP algorithm and fuzzy control strategy are compared. The results show that the fuzzy control strategy designed achieves the expected results and the design method is reasonable and effective. HEV; fuzzy control; dynamic programming; ISG *國家自然科學基金(51075411)資助。 原稿收到日期為2014年1月5日,修改稿收到日期為2014年3月27日。

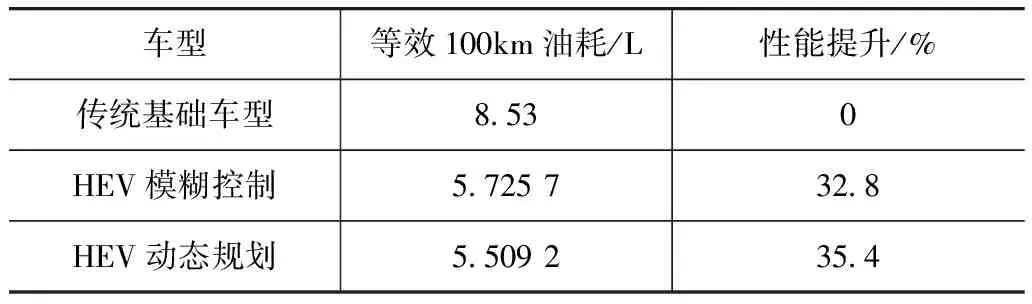
3 模糊控制策略設計

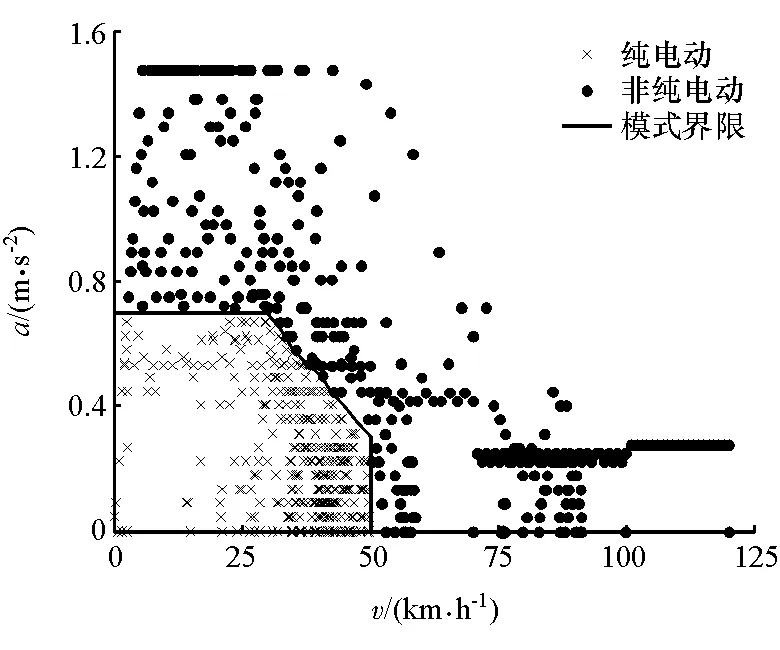
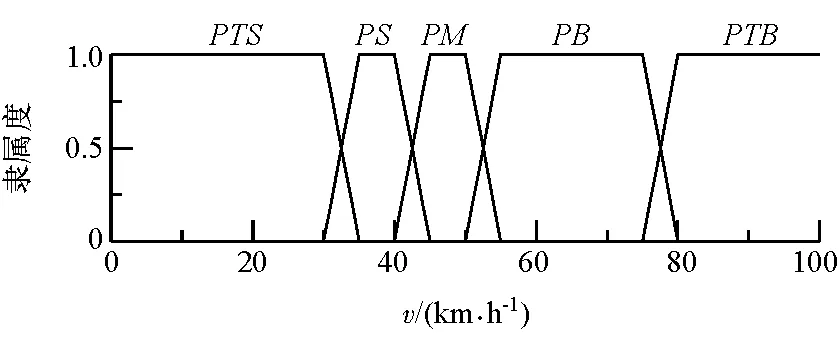
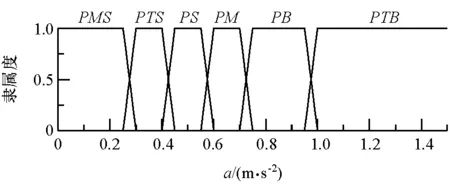





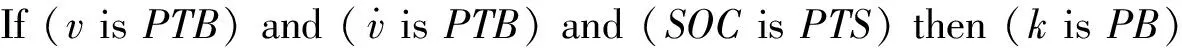

4 結論

