人群簡化模型與人行橋TMD參數設計研究

孫　昊， 周　叮， 劉偉慶， 李枝軍

(南京工業大學 土木工程學院，南京　211816)

?

人群簡化模型與人行橋TMD參數設計研究

孫昊， 周叮， 劉偉慶， 李枝軍

(南京工業大學 土木工程學院，南京211816)

摘要：用兩段連續彈性桿模擬靜立人體，建立人群-人行橋-調諧質量阻尼器(TMD)振動系統。將靜立人群簡化建模為單個的廣義人體，研究廣義人體-人行橋-調諧質量阻尼器振動系統的動力特性及TMD參數設計。運用最小二乘原理確定廣義人體的相關參數，通過與已有的實驗數據對比，驗證了將靜立人群簡化為廣義人體模型的正確性。以均方根加速度作為人體舒適度的優化準則，分析了人行橋TMD的最優頻率比和最優阻尼比。

關鍵詞：人群-人行橋-TMD系統；廣義人體-人行橋-TMD系統；最小二乘；最優頻率比；最優阻尼比

隨著建筑結構技術的迅速發展和高性能建筑材料的廣泛運用，人行橋正向大跨輕柔低阻尼的方向發展，人行橋的人致振動問題也因此日益突出。在主體結構下附加一個由彈簧、阻尼器和質量塊構成的TMD裝置，通過合理的參數設置可以減小或消除主體結構的有害振動。TMD主要適用于激勵力接近于諧振的情況，人體的腳步力具有擬周期性，人行橋的動力響應主要與橋的豎向基階模態相關[1]，因此，TMD適用于人行橋的減振控制。

與歌劇院樓蓋、賽場看臺一樣，劃船比賽沿線、煙花施放場所、公園景點和城市風光帶的人行橋上常常會聚集大量的站立人群。Ellis等[2]對Twickenham體育館的測試結果表明駐留人群應作為單自由度的質量-彈簧-阻尼器系統來考慮。靜立人群和行走人群對人行橋的影響是不同的，靜立人群會改變人行橋的動力學特性而行走人群會激發人行橋產生振動。目前，研究者已認識到有人駐留時系統的阻尼會有所增加[3]，而固有頻率可能增大也可能減少。然而，采用TMD實現人行橋減振控制的常規設計方案往往不考慮人體對人行橋的作用或者只是將人體考慮為附著于人行橋上的剛性質量，忽略人體彈性對人行橋動力特性的影響。因此，常規設計方案對人行橋的減振控制是不全面的。

本文利用生物力學相關知識，將靜立人體模擬為兩段連續彈性桿附加到人行橋上，將行人對人行橋的激勵簡化為作用于人行橋跨中的簡諧力，用以表達靜立人群和行走人群對人行橋的不同作用，建立了人群-人行橋-TMD系統與廣義人體-人行橋-TMD系統的控制微分方程組。通過對兩個系統方程組的比較分析，將人群簡化為單個的廣義人體模型。運用最小二乘原理確定廣義人體的相關參數。人體的不適反應主要來自振動加速度，因此使用均方根加速度法對TMD進行參數優化。

1人群-人行橋-TMD動力模型

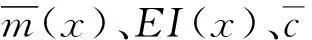
圖1　人群-人行橋-TMD模型Fig.1 The model of crowd-footbridge-TMD system

人行橋的動力響應主要與人行橋的豎向基階模態[1]有關，將人行橋的豎向位移近似為：

uS(x,t)=φ1(x)q1(t)

(1)

只考慮人體的基階模態并忽略人體腳部彈性與阻尼的影響，第j個靜立人體的豎向位移可表示為：

uHj(y,t)=uS(xj,t)+uRj(y,t)=

φ1(xj)q1(t)+uHRj(t)φ(y)

(2)

式中，φ1(x)和q1(t)分別為人行橋的豎向基階模態函數和模態坐標，uS(xj,t)為距離橋左端xj處人行橋的豎向位移，uRj(y,t)為第j人相對于人行橋的豎向位移，φ(y)為人體豎向振動的基階模態函數。

人群-人行橋-TMD系統的勢能為：

(3a)

人群-人行橋-TMD系統的動能為：

人群-人行橋-TMD系統的阻尼耗能為：

(3c)

行人腳步力做功為：

W=PS(t)φ1(L/2)q1(t)

(3d)

受迫振動的拉格朗日方程為：

(4)

將式(3a)～(3d)代入式(4)可得：

[K]{X(t)}={P(t)}

(5)

式中：{P(t)}={PS(t)φ1(L/2),0,0，…，0,0}T,

{X(t)}={q1(t),uHR1(t),uHR2(t)…uHRJ(t),uT(t)}T,

以及下列參數：

式中MS1、KS1、CS1分別為人行橋的豎向基階模態質量、模態剛度、模態阻尼，MH0為人體總質量，MH為人體的模態質量，MH1為人體與人行橋的耦合質量。當不考慮TMD時，式(5)自動蛻化為人群-人行橋系統的控制微分方程組。

2人體的模態參數

由生物力學知識可知，人體可用分段的連續彈性直桿近似模擬[5]，本文采用簡單的兩段直桿模型，設每段直桿的質量均布，沿豎直方向的剛度也均布，如圖2所示。

每個直桿的軸向振動微分方程為:

(6)

式中，mi和ki(i=1,2)為每段桿件的單位長度質量和軸向剛度。

式(6)的解為：

ui(x,t)=Usin(ωHt+φi)φi(x),i=1,2

(7)

式中:ωH為人體振動的角頻率，φi為相位角，φi(x)為模態，U為振動幅值。人體模型底部固定于人行橋上，頂部自由，利用上下兩段直桿連接處的變形協調條件，可以導出人體的模態。

φ1(x1)=Bsinb1x1,0≤x1≤h1,φ2(x2)=

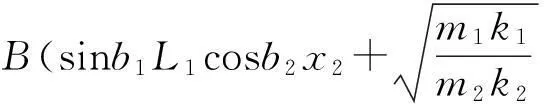
0≤x2≤h2

(8)

圖2　人體豎直方向的振動模型Fig.2 The model of a body vibrating in vertical direction

得到人體的頻率方程為:

(9)

考慮h1=h2并取m2=2m1,k2=2k1，該參數可較好地模擬人體[5]。由此導出特征值b1h1=0.615 5和人體的各等效質量為：MH1=0.765 9 MH0,MH=0.666 7 MH0。

3廣義人體-人行橋-TMD模型

圖3　廣義人體-人行橋-TMD模型Fig.3 The model ofgeneralized human-footbridge-TMD system

廣義人體-人行橋-TMD的耦合動力模型如圖3所示。考慮一具有分布質量mG(x)，分布剛度kG(x),分布線性黏滯阻尼cG(x)，高度為HG的廣義人體模型。設廣義人體靜立在人行橋的跨中。人行橋、TMD、荷載等條件與第1節相同，廣義人體同樣用分段連續彈性直桿模擬。僅考慮人行橋與廣義人體的基階模態，采用與第1節類似的分析過程，得到：

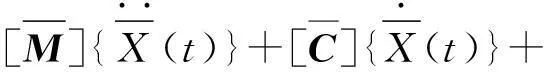
(10)

式中：

以及下列參數：

式中：MGH0為廣義人體的總質量，MGH為廣義人體的模態質量，MGH1為廣義人體與人行橋的耦合質量。當不考慮TMD時，式(10)蛻化為廣義人體-人行橋系統的控制微分方程組。

4廣義人體的模態參數

設J個靜立人體沿著人行橋跨中對稱站立，人體間距為0.5 m，由上述數據可得人群-人行橋系統的控制微分方程組為：

(11)

將人群簡化為廣義人體模型的關鍵是使人行橋的加速度響應在簡化前后保持一致。對比式(5)和(10)可發現當廣義人體與單個人體取如下關系時，兩公式相近：

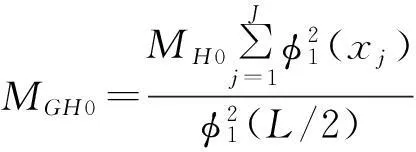
MGH=MH，MGH1=θMH1(θ為待定系數),KGH=KH,CGH=CH

根據上述數據參數，廣義人體-人行橋系統的控制微分方程組可轉化為：

(12)

5θ的確定與廣義人體模型的驗證

式(11)、(12)中的質量矩陣為非對角陣，因而無法通過經典的模態分解法進行解耦。本文采用等時間步長的有限差分法近似計算[12]，速度和加速度的中心差分可表示為：

(13)

(14)

將式(11)和(12)代入式(13)、(14)可以得到中心差分的迭代公式：

(15)

(16)

為了達到足夠的計算精度與收斂性，本文取時間步長Δt=0.01 s。

基于最小二乘原理，在給定靜立人數J后確定θ的方法為：在合理的θ取值范圍內，使得人群-人行橋與廣義人體-人行橋兩個系統中人行橋跨中加速度差的平方在一個周期內的和積分最小。即：

(17)

表1給出了不同靜立人數下的θ值。可以發現，隨著靜立人數J的增大，θ值也相應增大，但θ始終小于靜立人數J。這表明θ是由人行橋基階模態和各個人體的位置所決定的，而不是J個靜立人體的簡單疊加。

將不同靜立人數J所對應的θ值代入式(12)中，參考文獻[13]的解析解可求出廣義人體-人行橋系統的豎向基階模態頻率和豎向基階模態阻尼比。

表1　不同靜立人數下的θ值

表2給出了本文數值模擬結果與王海等[3]的人-梁模型及Sachse實驗結果的比較。由于實驗測得的人群-人行橋系統的基階頻率離散性較大，Sachse沒有給出其具體數值只是說明隨著簡支梁上靜立人數的增加，系統的基階頻率隨之下降[6-7]，這一定性趨勢與本文的計算結果相同。通過對受迫振動實驗得到的復頻反應函數進行曲線擬合，Sachse識別出了系統的豎向基階模態阻尼比，該結果與本文的計算結果較為接近。相對于王海、周叮的結果，本文系統的豎向基階模態頻率略有下降但阻尼比略有增加，這主要來自于二者的模型差異以及對人體阻尼比的取值不同。由此可見將人群簡化為單個的廣義人體模型是正確的。

圖4表明人群-人行橋系統與廣義人體-人行橋系統中人行橋跨中的加速度響應一致性很好。

圖4　簡化前后人行橋跨中加速度響應對比Fig.4 The comparison of acceleration time history at the midspan of footbridges before and after simplifying

靜立人數J系統的豎向基階模態頻率廣義人體-人行橋人-梁人群-人行橋計算值/Hz 計算值/Hz實驗系統的豎向基階模態阻尼比廣義人體-人行橋人-梁人群-人行橋計算值/%計算值/%實驗值/%14.44524.479基頻隨人數0.6280.5980.654.34144.362增加而下降1.8541.6801.7

6TMD的參數優化

Den Hartog[14]給出了TMD的最優頻率比和最優阻尼比為：

(18)

根據式(10)和第4節的相關數據，取步頻fP在正常步頻范圍(1.6～2.4 Hz)內變化，廣義人體-人行橋-TMD系統的控制微分方程組為：

(19)

將式(19)和廣義人體的相關參數代入式(16)，可得到關于步頻fp、質量比μ、頻率比β、阻尼比ξT的廣義人體-人行橋-TMD系統的時程解。

在正常步頻范圍內，固定質量比μ，以行人引起的人行橋最大均方根加速度最小作為準則[15]來確定最優頻率比βopt和最優阻尼比ξT,opt。識別準則：

(20)

均方根加速度為：

(21)

表3給出了不同靜立人數J和質量比μ下TMD的最優參數。通過對比發現，考慮靜立人體的彈性后，TMD的最優頻率比總是小于Den Hartog的解析解，而TMD的最優阻尼比總是小于等于Den Hartog的解析解。表3還表明，當靜立人數J不變時，本文識別出的最優頻率比隨著質量比μ的增大而減小，但最優阻尼比會增大。當質量比μ不變時，本文識別出的最優頻率比隨著靜立人數J的增大而減小。

表3　廣義人體-人行橋-TMD系統的

考慮人群腳步力的前二階諧波，圖5～7給出了靜立人數為5或15人時的計算結果。圖5、圖6表明在正常步頻范圍內，TMD的減振效果比較明顯。安裝TMD后，人行橋跨中的加速度響應被均勻化，在某些步頻下的減振效果尤為突出。圖7表明本文識別出的TMD最優參數的減振效果要優于Den Hartog的解析解，當靜立人數較多時減振效果更好。對于有大量駐立人群的景觀橋，本文的參數更為合理。

圖5　正常步頻范圍內TMD的減振效果Fig.5 The effects of reduced vibration of TMD in the range of normal step frequencies

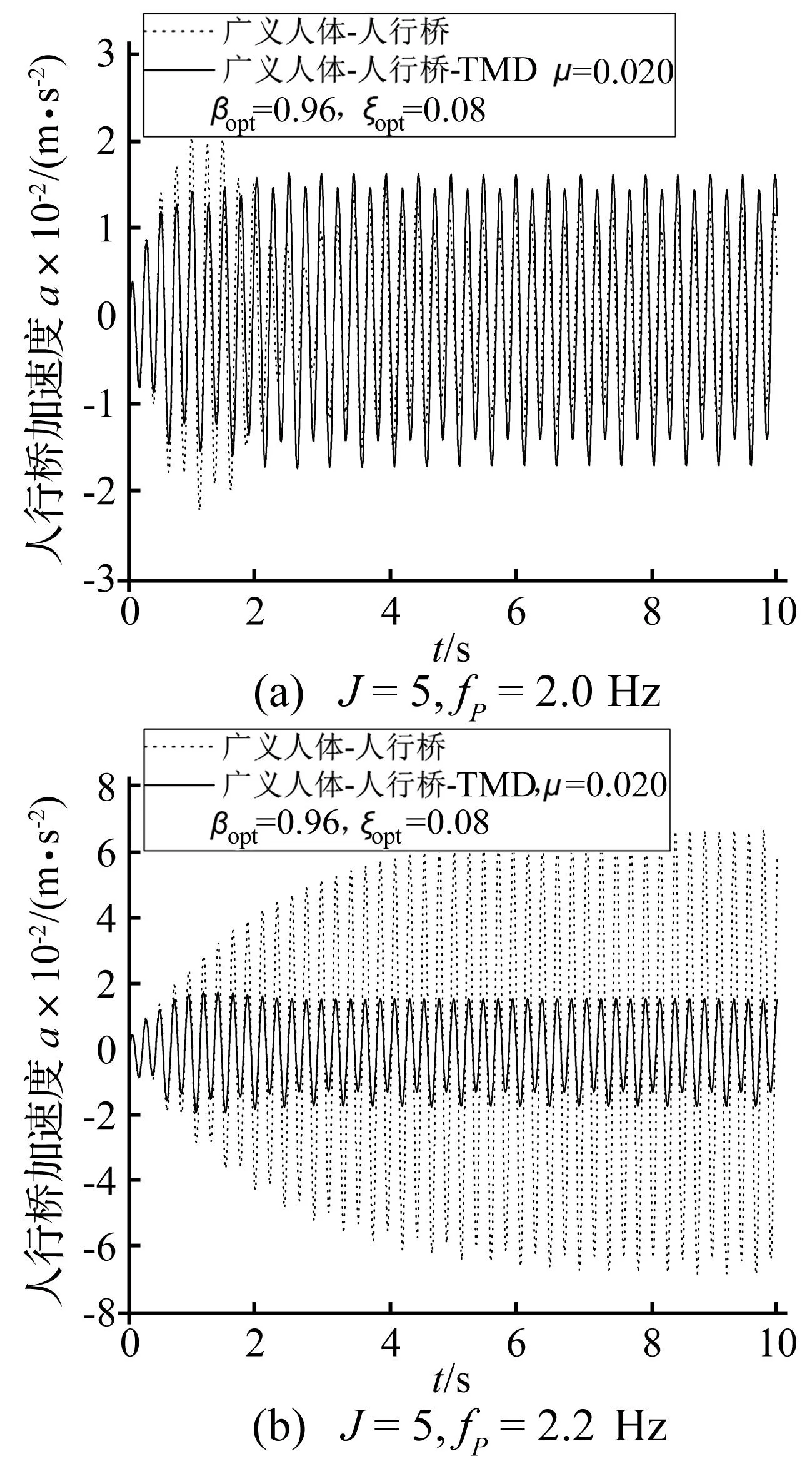
圖6　安裝TMD前后人行橋跨中加速度時程響應對比圖Fig.6 The comparison of acceleration time history at the midspan of footbridges with and without TMD

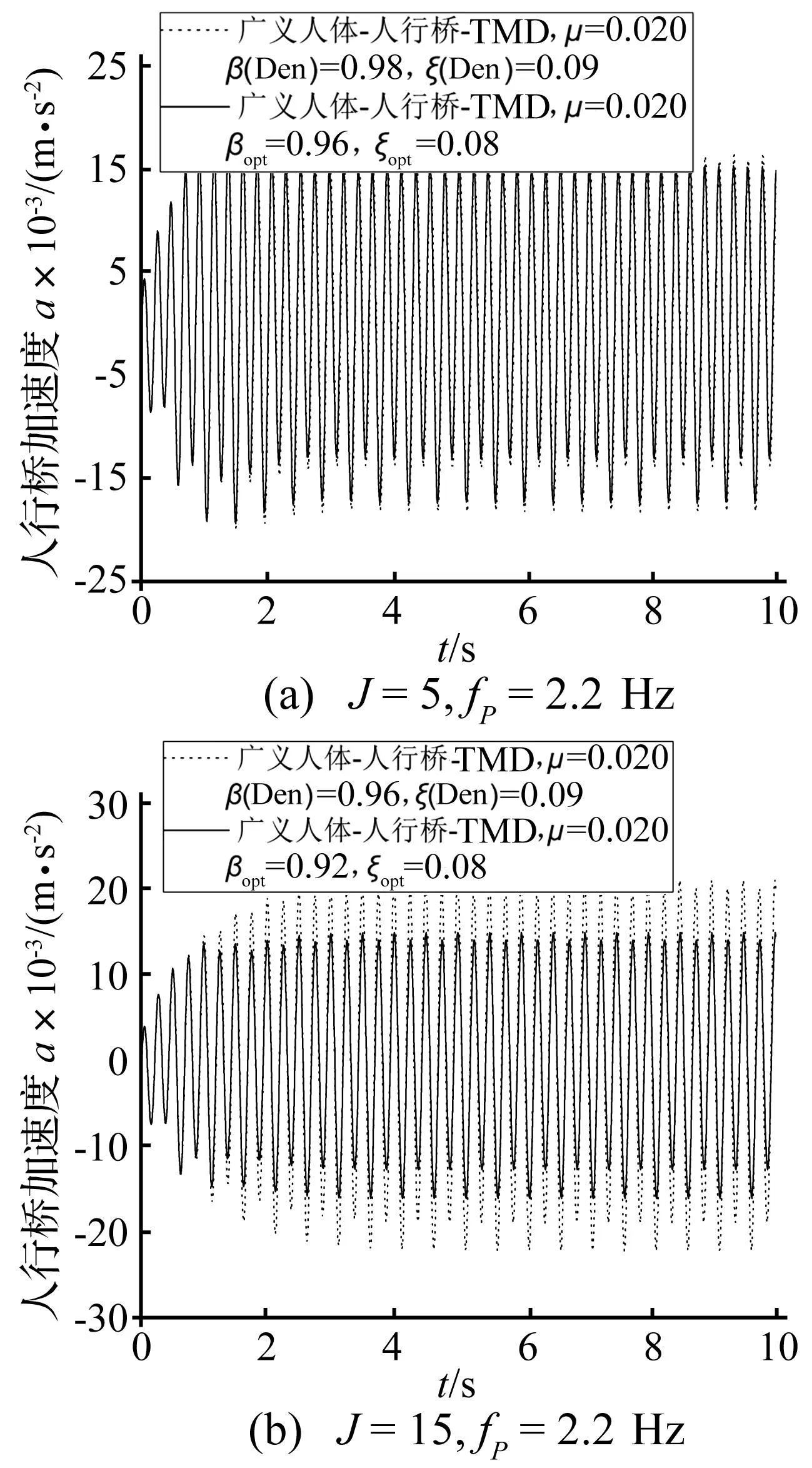
圖7　不同最優參數下人行橋跨中加速度的時程響應對比圖Fig.7 The comparison of acceleration time history at the midspan of footbridges with different optimal parameters

7結論

本文針對大跨人行橋TMD設計中的不足，提出在人行橋-TMD系統的基礎上考慮靜立人體的彈性，分別建立人群-人行橋-TMD模型和廣義人體-人行橋-TMD模型，得到如下結論：

(1) 將人群簡化為單個的廣義人體模型降低了系統的自由度，使得考慮人群-人行橋相互作用變得簡單。

(2) 運用最小二乘原理，廣義人體的相關參數可由人體的相關參數、人行橋基階模態和各個人體的位置確定。

(3) 考慮靜立人體的彈性后，TMD的最優頻率比總是小于Den Hartog的解析解，而TMD的最優阻尼比總是小于等于Den Hartog的解析解。當靜立人數J不變時，本文識別出的最優頻率比隨著質量比μ的增大而減小，但最優阻尼比會增大。當質量比μ不變時，本文識別出的最優頻率比隨著靜立人數J的增大而減小。

(4) 安裝TMD后，人行橋跨中的加速度響應被均勻化。對于城市風光帶處的人行橋，本文的最優參數效果更合理。

參 考 文 獻

[ 1 ] 陳宇，樊健生，聶建國.多跨人行橋振動的均方根加速度反應譜法[J]. 土木工程學報，2010，43(9):117-124.

CHEN Yu, FAN Jian-sheng, NIE Jian-guo. RMS acceleration response spectrum method for multi-span footbridge vibrations under pedestrian load [J]. Journal of Civil Engineering, 2010, 43(9): 117-124.

[ 2 ] Ellis B R, Ji T. Human-structure interaction in vertical vibrations [J]. Proceeding of the ICE: Structures and Buildings, 1997, 122(1): 1-9.

[ 3 ] 王海，周叮，王曙光.人-梁相互作用動力學模型研究[J]. 工程力學，2010，27(5):14-20.

WANG Hai, ZHOU Ding, WANG Shu-guang. Modeling of the dynamic interaction of human occupants and beam [J]. Engineering Mechanics, 2010, 27(5): 14-20.

[ 4 ] 閏興非，孫利民，袁旭斌，等.人行橋人致振動問題的計算模型對比分析[C]//中國振動工程學會.第八屆全國振動理論及應用學術會議論文集.上海:中國振動工程學會，2003年,1-8.

[ 5 ] Ji T. A continuous model for the vertical vibration of the human body in a standing position[C]// United Kingdom Informal Group Meeting on Human Response to Vibration. Bedford, UK: 1995.

[ 6 ] Sachse R. Modeling effects of human occupants on modal properties of slender structures [J]. The Structural Engineer, 2002, 80(5): 21-23.

[ 7 ] Sachse R. The influence of Human occupants on the dynamic properties of slender structures PHD [D]. Sheffield,UK: The University of Sheffield, 2002.

[ 8 ] Ebrahimpour A, Hamam A, Sack R L,et al. Measuring and modeling dynamic loads imposed by moving crowds [J]. Journal of Structural Engineering,1996, 122(12): 1468-1474.

[ 9 ] 孫利民，閆興非. 人行橋人行激勵振動及設計方法[J]. 同濟大學學報：自然科學版，2004,32(8):996-999.

SUN Li-min, YAN Xing-fei. Human walking induced footbridge vibration and its serviceability design[J]. Journal of Tongji University: Natural Science, 2004, 32(8): 996-999.

[10] Matsumoto Y, Nishioka T, Shiojiri H, et al. Dynamic design of footbridges[M]. Zurich: IABSE, 1978.

[11] Sachse R, Pavic A, Reynolds P. Human-structure interaction in civil engineering dynamics: a literature review [J]. The Shock and Vibration Digest, 2003, 35(1): 3-18.

[12] Chopra A K.結構動力學：理論及其在地震工程中的應用[M]. 謝禮立，呂大剛,譯.北京:高等教育出版社，2007.

[13] Zhou Ding, Ji Tian-jian, Liu Wei-qing. Dynamic characteristics of a standing human on a SDOF [J]. Advances in Engineering, 2012, 11(1): 85-98.

[14] Den Hartog J P. Mechanical vibrations [M]. New York: Dover Publications, 1947.

[15] 樊健生，陳宇，聶建國.人行橋的TMD減振優化設計研究[J]. 工程力學，2012，29(9):133-140.

FAN Jian-sheng, CHEN Yu, NIE Jian-guo. Optimum design of tuned mass damper for footbridge[J]. Engineering Mechanics, 2012, 29(9): 133-140.

Simplified model of human crowd and parameter design of TMD for footbridges

SUNHao,ZHOUDing,LIUWei-qing,LIZhi-jun

(College of Civil Engineering, Nanjing Tech University, Nanjing 211816, China)

Abstract:Here, a continuous-elastic bar with two segments was used to model bodies standing on a footbridge and the crowd-footbridge-tuned mass damper (TMD) vibration system was built. By simplifying the static crowd as a generalized human body, the dynamic characteristics of the generalized human body-footbridge-TMD system and the parameter design of TMD were studied. The parameters of the generalized human body were identified with the principle of least square. Comparing with the data available from tests, the correctness of the simplified generalized human body was verified. The root-mean-square acceleration was taken as the optimization criterion to assess the human body comfort, the optimal parameters of the TMD were analyzed.

Key words:crowd-footbridge-TMD system; generalized human body-footbridge-TMD system; least square; optimal frequency ratio; optimal damping ratio

中圖分類號:TU3；TB1

文獻標志碼：A

DOI:10.13465/j.cnki.jvs.2016.04.035

通信作者周叮 男，博士，教授，博士生導師，1957年生

收稿日期：2014-07-14修改稿收到日期：2015-01-20

基金項目：國家自然科學基金(11372127;51208252)；江蘇省屬高校自然科學研究重大項目(12KJA580002)

第一作者 孫昊 男，碩士生，1989年生

E-mail：dingzhou57@yahoo.com