空天飛機再入軌跡的變精度序列優化方法

朱俊杰，余雄慶，羅東明，王宇

南京航空航天大學 飛行器先進設計技術國防重點實驗室，南京 210016

空天飛機再入軌跡的變精度序列優化方法

朱俊杰，余雄慶*，羅東明，王宇

南京航空航天大學 飛行器先進設計技術國防重點實驗室，南京 210016

為提高空天飛機再入軌跡優化方法的穩健性和精度，提出一種變精度序列優化方法。優化計算過程分為3個步驟：首先進行預優化，即在粗離散情況下，應用混合優化方法進行軌跡優化，獲得各時間點設計變量的最優解；然后對預優化的結果進行一元全區間插值處理，獲得細離散情況下設計變量的初值；最后進行精細優化，獲得精度更高的計算結果。算例結果表明，變精度序列優化方法能穩健地求解空天飛機再入軌跡優化問題,并能以較少的計算量獲得滿足精度要求的優化結果。

空天飛機；再入軌跡；優化；混合優化；插值

空天飛機軌跡優化是在飛行動力學和物理學約束的條件下，尋求最優解的過程，它貫穿于整個空天飛機設計過程中，影響著總體、氣動布局、制導控制、動力和結構等多個分系統的設計，對空天飛機的研制具有重要意義。

軌跡優化是一類最優控制問題，屬于復雜的大規模非線性優化范疇。軌跡優化設計方法主要有基于極大值原理的間接法和基于非線性規劃理論的直接法。間接法的優點是計算精度高，并且能夠滿足最優必要性條件，但由于繁雜的數學推導和難于求解的兩點邊值問題，目前已很少使用間接法求解軌跡優化問題。隨著計算機技術的發展，目前的研究更傾向于使用直接法求解。在采用直接法求解軌跡優化問題時，先將最優控制問題轉化為非線性規劃問題(Nonlinear Programming, NLP)，對控制變量和狀態變量進行離散，對狀態方程、端點約束以及路徑約束進行節點轉化，再選擇優化算法求解決策向量和目標函數。

對于優化算法來說，目前主要采用兩種優化算法：1)經典優化算法，例如序列二次規劃算法(Sequential Quadratic Programming， SQP)[1]、梯度下降法、罰函數方法[2]等；2)智能優化算法，例如遺傳算法[3-4](Genetic Algorithm，GA)、進化策略(Evolution Strategy， ES)、粒子群優化(Particle Swarm Optimization， PSO)等。經典優化算法的優點是收斂速度快，但是需要給出合理的初始值，才能收斂到最優解。對于空天飛機再入軌跡問題，有數百甚至數千個設計變量。面對這么多變量，以人工方式給出一個合理的初始值幾乎不可能。智能優化算法的優點是無需給出初值，穩健性好，但收斂速度慢，優化結果不夠精確。為了克服經典優化算法和智能優化算法的缺點，近年來有學者提出了混合優化方法[5]，即首先用智能優化算法獲得一個初步優化結果，然后以該結果為初始點，利用經典優化算法，快速搜尋最優解。如Vavrina采用GA與SQP相結合的方法求解低推力軌跡優化問題[6]。但是，對于空天飛機再入軌跡優化問題，我們發現，當時間配點數較多時，混合優化方法也不能可靠地求解軌跡優化問題，其穩健性不能令人滿意。

本文借鑒計算流體力學中預處理思路(變精度網格方法[7])，提出了一種變精度序列優化方法，目的是為空天飛機再入軌跡優化提供一種穩健的、收斂速度快且精度高的方法。

1 再入軌跡優化問題的描述

1.1 運動方程的建立

空天飛機再入大氣層時的三自由度運動學和動力學方程組為[8-9]

(1)

式中：m為空天飛機質量；R為空天飛機質心到地心的距離；φ為經度；θ為緯度；v為速度；γ為航跡角；ψ為航跡方向角；β為傾側角；D為阻力；L為升力；g為重力加速度。

D,L，g,H分別為

(2)

(3)

(4)

(5)

式中：g0=9.8 m/s2為地球表面的重力加速度；ρ為大氣密度；H為空天飛機離地面高度；R0=6 357 km為地球半徑；S為空天飛機參考面積；CD和CL分別為阻力系數與升力系數。

在大氣飛行過程中的熱流密度為[10]

(6)

式中：RN為飛行器頭部前緣半徑。

動壓為

(7)

過載為

(8)

1.2 歸一化處理

對于再入軌跡優化問題，不同變量之間的數值量級相差較大，例如R是106級別，而經度和緯度化為弧度后是1～10級別，二者數值上相差太大，會導致數值奇異，使優化計算失敗。為了增加優化計算的穩健性，需要對原始模型進行歸一化處理。令

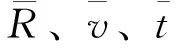
(9)

升力和阻力按如下方法歸一化處理：

(10)

(11)

1.3 空天飛機再入軌跡優化問題

(1)設計變量

對于升力式再入航天器的軌跡優化問題，由于航天器再入后依靠升力在大氣層內做較長時間的滑翔，通過改變姿態來控制氣動力的變化，以完成軌跡的調整和機動，因此通常將迎角α和傾側角β作為控制變量。再入航天器的飛行軌跡可由航天器質心到地心的距離R、經度φ、緯度θ、速度v、航跡角γ、航跡方向角ψ等參數來描述，這組參數即為狀態變量。控制變量和狀態變量均是時間的函數，而狀態變量隨時間的變化是由微分形式的飛行動力學方程支配的。軌跡優化問題的設計變量由每個時間微段的控制變量和狀態變量組成。

(2)優化目標

優化目標的選擇主要由航天器的設計及任務要求確定，通常有如下幾種優化目標：1)以飛行航程最大作為性能指標；2)以再入過程中總吸熱量最小作為性能指標[12]；3)以最小能量消耗作為性能指標[13]；4)以到達指定目標點飛行時間最短為優化的性能指標。

(3)約束條件

再入軌跡優化中的約束包括終端約束、過載、動壓及熱流峰值約束和控制量約束[12]等。

(4)空天飛機再入段描述

再入段是引導空天飛機從巡航高度轉至末端區域能量管理段的無燃料消耗飛行階段，可視為常質量的無動力滑翔，再入段內無論高度還是速度都表現出遞減的趨勢，飛行包線呈收斂的走廊狀。再入過程的初始段保持大迎角飛行姿態，且大氣密度較小，空氣動力作用不明顯，但此時空天飛機具有很高的速度，因此首先受到熱流約束的限制。再入飛行應最大限度地利用機體表面的防熱材料，使空天飛機處于熱流峰值的合理范圍，并利用地球大氣降低飛行速度，使其盡快通過高熱流區域。再入過程的后半段處于稠密大氣層中，空氣動力的作用明顯增強，動壓和過載的共同約束逐漸加強。

2 變精度序列優化方法

“變精度”是指用粗離散(離散配點數較少)和細離散(離散配點數較多)2種方式對飛行時間進行離散。變精度序列優化方法的思路是：首先在粗離散情況下，應用混合優化方法進行軌跡優化，獲得各時間點設計變量的初步優化結果；然后對初步優化結果應用插值處理方法，獲得細離散情況下各設計變量的初始值；最后，在細離散情況下，應用經典優化算法，獲得精度更高的優化結果。

智能優化算法采用一種最近新發展的優化方法——子集模擬優化算法[14]。有關研究表明：與GA相比，子集模擬優化算法具有更快的收斂速度[15]。經典優化算法采用SNOPT程序[16]，該程序采用了一種改進的SQP，適用于求解大規模非線性稀疏優化問題。

變精度序列優化方法的主要步驟如下：

(1)預優化

將飛行時間進行粗離散，應用混合優化算法求解軌跡優化問題。在粗離散過程中，離散時間段過多，則優化效率比較低；而離散點太少的話，得到的原始優化結果則不能足夠準確地反應整個飛行過程，將這個原始優化結果作為后續SNOPT運算的初始值時SNOPT程序可能不會收斂。對于本文的問題，建議將飛行時間劃分成20個時間微段。具體來說，首先采用智能優化算法迭代計算若干步(比如迭代100步、200步等)，計算結果不一定收斂，可以得到一個原始優化結果；然后以該原始優化結果作為SNOPT優化過程的初始值，進行優化計算直至收斂，獲得初步優化結果。

(2)插值計算

根據軌跡設計精度的要求，進行細離散。對預優化的結果進行一元全區間插值處理，獲得細離散情況下設計變量的值，然后將這個值設為精細優化的初始值。

(3)精細優化

在細離散情況下，應用SNOPT程序獲得精度更高的計算結果。其中優化計算的初值為上一步插值計算中確定的初始值。變精度序列優化算法的流程如圖1所示。

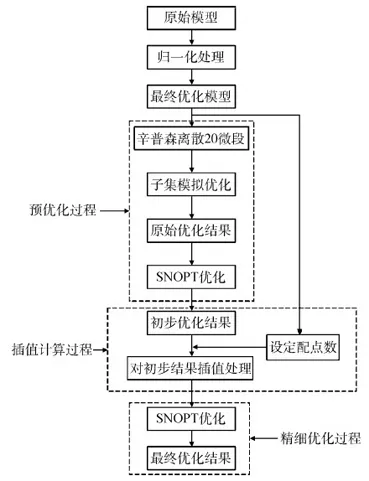
圖1 變精度序列優化算法流程Fig.1 Variable-fidelity sequential optimization method flowchart

上述優化策略的優點是：既解決了空天飛機軌跡優化過程迭代初始值不易給定的問題，又可避免現有混合優化方法在離散配點數較大情況下不夠穩健的缺點。

3 算例與驗證

3.1 算例

空天飛機再入軌跡優化算例取自文獻[17-18]，并在原始算例基礎上增加了熱流密度約束、動壓約束和過載約束。

該飛行器的氣動模型為

空天飛機參考面積和質量分別為S=250.237 m2、m=92 162 kg。空天飛機前緣半徑為RN=1 m。不同高度下大氣相關參數參考文獻[19]。

該優化問題的初始狀態為R=6 436 100 m，φ=0°,θ=0°,v=7 808 m/s,γ=-1°,ψ=90°。

末端狀態為R=6 381 200 m,v=762.5 m/s,γ=-5°。

狀態變量的約束為[17]

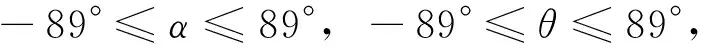
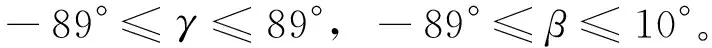
需要注意的是，這里的變量約束范圍并未考慮工程實際情況，而是默認為在理想狀態下，控制系統可以達到要求。

熱流密度、動壓、過載約束分別為

優化目標通過控制迎角α和傾側角β使航程Ra最遠。事實上，對于本算例來說，只需使末端緯度達到最大，就能使航程最遠。故為方便起見，以末端緯度最大作為優化目標J：

J=maxθ(tf)

式中：θ(tf)為末端時刻tf的緯度。設計變量包括控制變量(迎角和傾側角)和狀態變量(參見1.3節)。

3.2 計算過程和結果分析

本算例中離散方法采用辛普森離散法。優化計算過程如下：

1)預優化。將時間離散成20段，采用子集模擬優化算法，迭代計算100步，得到原始優化結果(10s內就能計算完畢)。子集模擬優化算法的參數設定為：單層樣本量取為100；條件概率取為0.51；最大層數取為100；終止精度取為10-6。

將子集模擬優化算法得到的原始優化結果作為SNOPT優化的初始點，進行優化計算，得到初步優化結果。

2)插值計算。將整個飛行時間離散為更多的時間微段。本算例考察了多種細離散情況，將整個飛行時間分別離散為30、50、60，80、100、150、200個時間微段。根據預優化后得到的結果，利用插值計算，獲得各種細離散情況下設計變量的初始值。

3)精細優化。對于各種細離散情況，進行精細優化，優化結果見表1。計算機配置為3.10GHz,內存為2GB。從表1中可以看出，隨著時間離散微段的增加，迭代步數總的趨勢是逐漸增加的，精細優化時間也逐漸增加，得到的優化結果略有不同，目標值逐漸小幅上升。當時間離散為150個微段以上后，優化結果幾乎不變，說明該離散段數足以滿足精度要求。

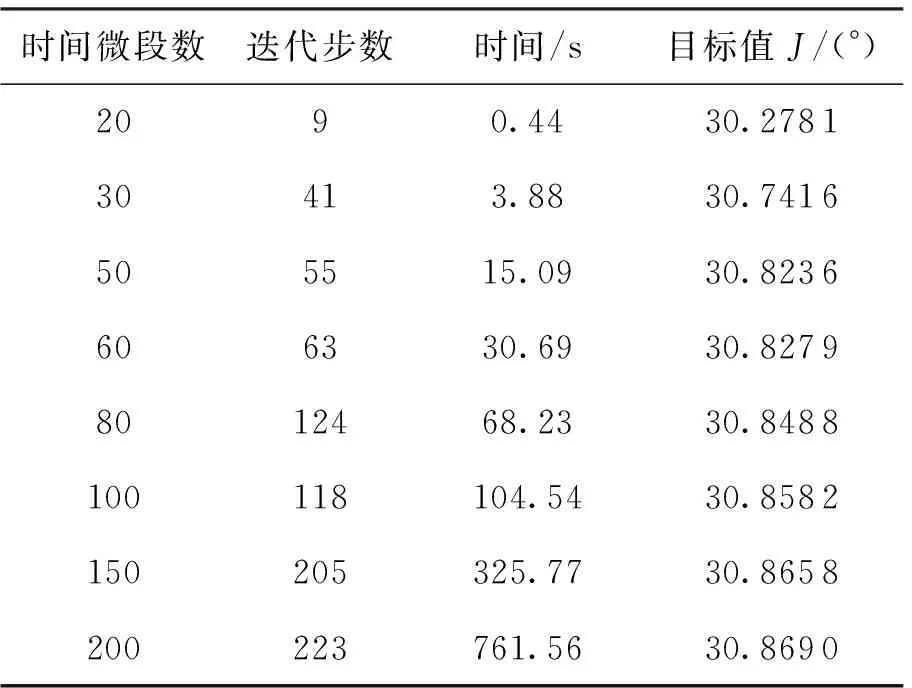
表1 不同離散情況下精細優化結果

精細優化(細離散為200個時間微段)的優化結果軌跡如圖2～圖7所示。

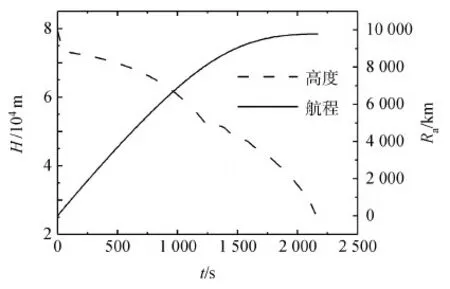
圖2 高度、航程時間關系Fig.2 Trajectory time histories for height and range

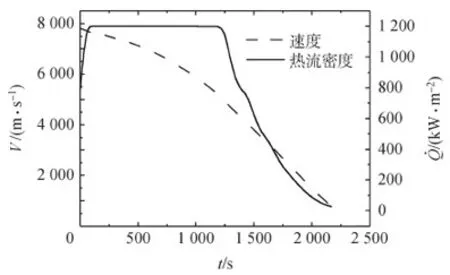
圖3 速度、熱流密度時間關系Fig.3 Trajectory time histories for velocity and heat flux

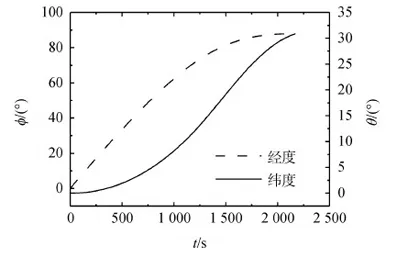
圖4 經度、緯度時間關系Fig.4 Trajectory time histories for longitude and latitude

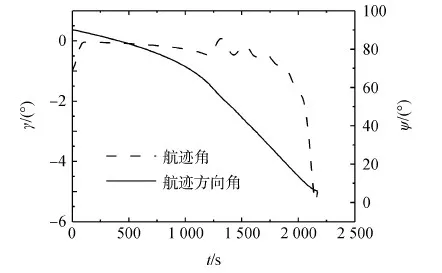
圖5 航跡角、航跡方向角時間關系Fig.5 Trajectory time histories for flight path angle and azimuth

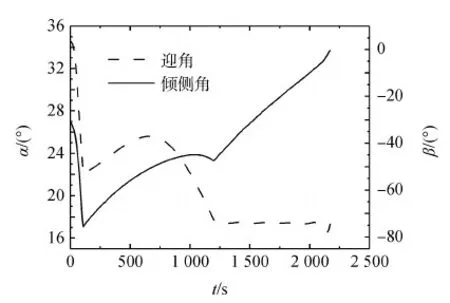
圖6 迎角、傾側角時間關系Fig.6 Trajectory time histories for angle of attack and bank angle

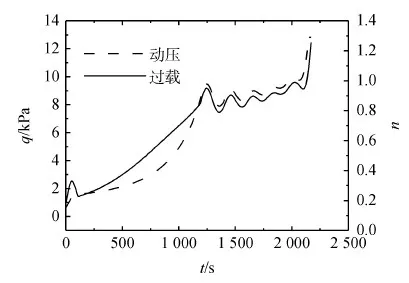
圖7 動壓、過載時間關系Fig.7 Trajectory time histories for dynamic pressure and overload

從圖2～圖5可以看出隨著再入飛行過程的進行，高度、速度、航跡方向角均呈現下降趨勢；航程、經度、緯度呈上升趨勢；航跡角變化平穩，逐漸下降，且始終保持在小角度范圍內，易于滿足飛行過程的平衡要求。從圖6可以看出下滑初期迎角較大，隨著再入飛行過程的繼續，迎角急劇減小，最后穩定在大約17°左右。這是由于在下滑初期，大氣密度很低，操縱面氣動效率較低，需要采用大迎角飛行。隨著高度的降低，大氣密度增大，當氣動力能夠克服重力后，軌跡進入一種近似滑翔的狀態，迎角穩定在相對較小的角度；從傾側角的變化曲線可以看出傾側角變化相對平滑，易于控制，且滿足控制量約束條件，下滑初始段，大傾側角(絕對值最大達到78°左右)可防止再入時的軌跡跳躍，有利于盡快建立動壓進入近似平衡滑翔狀態，最后隨著迎角降低，航向穩定性增大，橫航向耦合下降，慢慢恢復至小傾側角狀態。從圖3可知，在開始階段，由于速度過大，熱流密度急劇增加，一直增加到了約束最大值。雖然此后速度在減小，但是隨著高度的降低，大氣密度卻在增加，所以導致熱流密度一直保持在較大值。隨著飛行過程的延續，在速度和大氣密度的共同作用下，熱流密度才逐漸減小。從圖7中動壓曲線可以看出，返回初期在很大的高度范圍內動壓較低，高度的降低導致大氣密度呈指數增加，使動壓呈指數增大，后來隨著密度和速度的相互作用，動壓呈現出一定的振蕩特征，但始終在約束范圍內；過載也呈現出遞增趨勢，由于在下滑初始階段，迎角和速度比較大，大氣密度也急劇增加，導致氣動力急劇增大，過載急劇增加；后來在迎角、速度和大氣密度的共同作用下，過載增加逐漸變緩，也呈現出一定的振蕩現象，但仍在約束值3.0以內。

4 結束語

為了提高空天飛機再入軌跡優化的穩健性和精度，提出了一種變精度序列優化方法。變精度序列優化方法不僅可以用于空天飛機軌跡優化，其他大規模非線性優化問題也可以參考這種新的優化策略。最后用典型算例驗證了這種方法的有效性，結果表明：

1)通過預優化，可為精細優化提供一個合理的初始值，解決了空天飛機優化過程迭代初始值難以給定的問題。對于不同配點數的細離散情況，精細優化計算過程均可收斂，獲得優化結果，說明該方法具有很好的穩健性。

2)在精細優化中，當離散成200個時間微段時(離散后有1 609個設計變量，有1 803個約束方程)，僅僅迭代了223步就能收斂，優化計算效率高。

3)通過細離散和精細優化，可獲得滿足精度要求的優化結果。

References)

[1] 谷良賢, 趙吉松. 基于網格細化技術的地球-火星轉移軌道優化[J]. 中國空間科學技術, 2013, 33(6): 17-25.

GU L X, ZHAO J S. Earth-to-Mars transfer orbit optimization based on mesh refinement[J]. Chinese Space Science and Technology, 2013, 33(6):17-25(in Chinese).

[2] 陳功, 傅瑜, 郭繼峰.飛行器軌跡優化方法綜述[J].飛行力學, 2011,29(4): 1-5.

CHEN G, FU Y, GUO J F. Survey of aircraft trajectory optimization methods[J]. Flight Dynamics, 2011, 29(4): 1-5(in Chinese).

[3] 胡海龍，南英，聞新.基于遺傳算法的航天器再入動態終跡圈研究[J].中國空間科學技術, 2014, 34(1):35-41.

HU H L, NAN Y, WEN X. Research on dynamic reentry footprint for the spacecraft based on the genetic algorithm[J]. Chinese Space Science and Technology, 2014, 34(1):35-41(in Chinese).

[4] 閔學龍, 潘騰, 郭海林. 載人航天器深空飛行返回再入軌跡優化[J].中國空間科學技術, 2009, 29(4):8-12.

MIN X L, PAN T, GUO H L. Reentry trajectory optimization for manned deep space exploration[J]. Chinese Space Science and Technology, 2009, 29(4): 8-12(in Chinese).

[5] ZHANG D N, LIU Y. RLV reentry trajectory optimization through hybridization of an improved GA and a SQP algorithm[C]∥AIAA Guidance, Navigation, and Control Conference, 2011.

[6] VAVRINA M A，HOWELL K C. Global low-thrust trajectory optimization through hybridization of a genetic algorithm and a direct method[C]∥AIAA/AAS Astrodynamics Specialist Conference and Exhibit. Honolulu:[s.n.],2008: 1-27.

[7] BAGAI A, LEISHMAN J G. Adaptive grid sequencing and interpolation schemes for helicopter rotor wake analyses[J]. AIAA Journal, 1998,36(9): 1593-1602.

[8] RAHIMI A, KUMAR K D, ALIGHANBARI H. Particle swarm optimization applied to spacecraft reentry trajectory[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(1): 307-310.

[9] ZHANG K N, CHEN W C. Reentry vehicle constrained trajectory optimization[C]∥The 17th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, 2011.

[10] 吳德隆,王小軍.航天器氣動力輔助變軌動力學與最優控制[M]. 北京：中國宇航出版社,2006.

[11] 雍恩米, 唐國金, 陳磊.基于Gauss偽譜方法的高超聲速飛行器再入軌跡快速優化[J].宇航學報, 2008, 29(6):1766-1772.

YONG E M, TANG G J, CHEN L. Rapid trajectory optimization for hypersonic reentry vehicle[J]. Journal of Astronautics, 2008, 29(6):1766-1772(in Chinese).

[12] 湯亮, 楊建民, 陳風雨. 多約束條件下的升力滑翔式再入軌跡優化[J]. 導彈與航天運載技術, 2013(1):1-5.

TANG L, YANG J M, CHEN F Y. Trajectory optimization with multi-constraints for a lifting reentry vehicle[J]. Missiles and Space Vehicles, 2013(1):1-5(in Chinese).

[13] 陳剛,萬自明,徐敏,等.飛行器軌跡優化應用遺傳算法的參數化與約束處理方法研究[J].系統仿真學報,2005,17(11):2737-2740.

CHEN G,WAN Z M, XU M, et al. Parameterization method and constraints transformation method for RLV reentry trajectory optimization using genetic algorithm[J]. Journal of System Simulation, 2005, 17(11):2737-2740(in Chinese).

[14] LI H S, AU S K. Design optimization using subset simulation algorithm[J]. Structural Safety, 2010, 32(6): 384-392.

[15] LI H S. Subset simulation for unconstrained global optimization[J]. Applied Mathematical Modelling, 2011, 35(10): 5108-5120.

[16] GILL P E, MURRAY W, SAUNDERS M A. User′s guide for SNOPT Version 7: Software for large-scale nonlinear programming[R].San Diego:University of California,2010.

[17] ZONDERVAN K P, BAUER T P, BETTS J T, et al. Solving the optimal control problem using a nonlinear programming technique Part 3: Optimal shuttle reentry trajectories: AIAA-1984-2039[R]. Reston: AIAA, 1984.

[18] BETTS J T. Practical methods for optimal control and estimation using nonlinear programming[M].Philadelphia: SIAM Press, 2010.

[19] 楊炳尉.標準大氣參數的公式表示[J].宇航學報, 1983(1):83-86.

YANG B W. Formulization of standard atmospheric parameters[J]. Journal of Astronautics,1983(1):83-86(in Chinese).

(編輯：車曉玲、范真真)

A variable-fidelity sequential optimization method for reentry trajectory of space plane

ZHU Junjie,YU Xiongqing*,LUO Dongming, WANG Yu

KeyLaboratoryofFundamentalScienceforNationalDefense-AdvancedDesignTechnologyofFlightVehicle,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China

A variable-fidelity sequential optimization method for reentry trajectory design of a space plane was proposed to increase robustness and accuracy of the optimization. The optimization process consisted of three steps. Firstly,there was a pre-optimization, in which for a coarse discrete case, the optimal solution of design variables for each discretized point was obtained by using a hybrid optimization method. Secondly,initial values of the discretized points in a refined discrete case were obtained by using linear interpolation from the pre-optimization solution. Finally, the trajectory optimization in the refined discrete case was conducted, and more accurate optimization results were obtained. A demonstration example was used to validate the proposed method. The results indicate that the reentry trajectory optimization problem can be solved robustly with satisfied accuracy and less computational burden.

space plane; reentry trajectory; optimization; hybrid optimization; interpolation

10.16708/j.cnki.1000-758X.2016.0032

2015-09-01；

2015-11-11；錄用日期：2016-02-24；

時間：2016-04-29 10:49:39

http:∥www.cnki.net/kcms/detail/11.1859.V.20160429.1049.003.html

朱俊杰(1989-)，男，碩士研究生，1248400207@qq.com，主要研究方向為飛行器總體設計

*通訊作者：余雄慶(1965-)，男，教授，yxq@nuaa.edu.cn，主要研究方向為飛行器多學科優化設計和總體設計理論

朱俊杰,余雄慶,羅東明,等.空天飛機再入軌跡的變精度序列優化方法[J].中國空間科學技術,2016, 36(3):

50-56.ZHUJJ,YUXQ,LUODM,etal.Avariable-fidelitysequentialoptimizationmethodforreentrytrajectoryofspaceplane[J].ChineseSpaceScienceandTechnology, 2016, 36(3)：50-56(inChinese).

V221.6

A

http:∥zgkj.cast.cn