Banach空間上分數階積分微分方程的可解性與可控性

高媛

（蘭州交通大學數理學院，甘肅　蘭州　730070）

?

Banach空間上分數階積分微分方程的可解性與可控性

高媛

（蘭州交通大學數理學院，甘肅蘭州730070）

摘要：研究了Banach空間上一類具有非局部初始條件的分數階積分微分方程的可解性與可控性。借助合適的不動點定理，本論述建立了適度解的存在性和可控性條件，變換非局部柯西問題（1）為等效的積分方程，并且通過使用阿爾澤拉-阿斯科利定理和Krasnoselskii不動點定理獲得積分微分方程（1）的適度解。同時構建合適的控制函數，討論了滿足非局部初始條件的一類抽象積分微分發展方程（2）的可控性，最后舉例論證了定理2.1的一個簡單應用。

關鍵詞：非局部條件；積分微分方程；適度解；可控性

DOI10.3969/j.issn.1672-6375.2016.02.022

0　引言

早在1993年，Miller和Ross就提出了分數階的積分和微分[1]。之后，Podlubny又對分數階微分方程做了詳盡介紹[2]。此外，分數階微分方程的相關發展也包括：文獻[3]研究了二階中立性積分微分方程解的存在性，[4]則研究了脈沖微分方程與積分微分方程解的存在性,在此基礎上，[5]研究了脈沖偏微分方程適度解的存在性。但是在實際的問題和數學模型中，受局部條件和非局部條件的限制，文獻[6]的主要結論是不能被應用的。本論述第三部分在文獻[12]的基礎上，討論了形式如

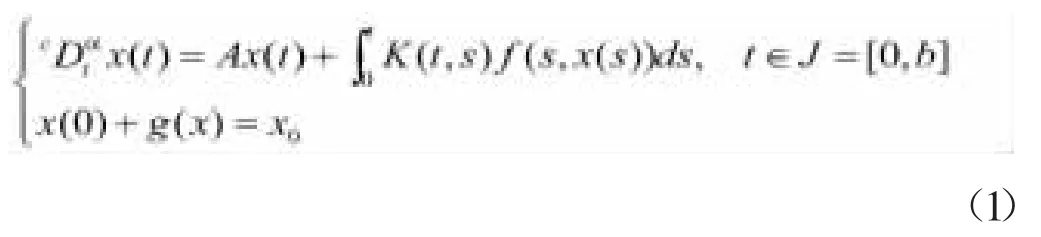
滿足非局部初始條件[8]的一類抽象分數階積分微分方程的可解性，其中是階Caputo分數階導數，x(·)在Banach空間X上取值，A是解析算子族的無窮小生成元，設，f，g是下文合適定義的函數，。

可控性[9]是數學控制理論的基本概念之一，可控性理論在有限和無限維系統中都扮演重要的角色，從[10]中可以發現諸多學者在研究無限維積分微分方程的可控性的同時也指出了隨機微分方程的可控性。最近，分數階微分方程的可控性變得越來越活躍了，[11]在研究分數階發展方程的完全可控性時所采用的技巧是分數階積分解算子的性質和不動點原理。受上面文獻的啟發和激勵，為了更進一步，本論述第三部分也研究了形式如

具有非局部初始條件的一類抽象分數階積分微分發展方程的可控性，滿足條件：是階Caputo導數，x(·)在Banach空間X上取值。由L2（J,U）獲得控制函數u(·)，滿足U是一個Banach空間。B是一個從U到 X的有界線性算子，A是解析算子族的無窮小生成元。設，f，g是下文合適定義的函數。本論述通過使用適度解一個更普遍的概念，建立了方程（2）的可控性條件。

1　預備知識

本節介紹了貫穿全文的符號、定義、注釋、引理，并且給出了方程（1）適度解[7]的定義，最后給出了證明主要結果用到的假設。

設C（J，X）是從J到X的連續函數的Banach空間，滿足范數

設B（X）表示從X到X的有界線性算子的Banach空間。

一個可測函數x:J→X是Bochner積分[13]，當且僅當是勒貝格可積的。

設L1（J，X）表示連續函數x:J→X（其中x是Bochner可積的）的Banach空間，滿足對于所有的x∈L1（J，X），范數

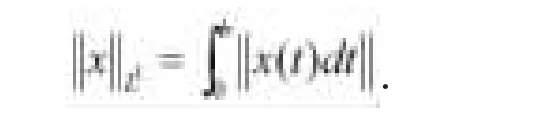
L（X）表示從X到它自身的所有有界線性算子的空間，D（A）表示A的定義域，ρ（A）表示A的預解集。是一致有界線性算子緊解析半群的無窮小生成元，且設0∈ρ（A），R（λ，A）=（λI-A）-1代表A的預解算子。

定義1.1.[2]下限為a的p階分數階積分定義為：

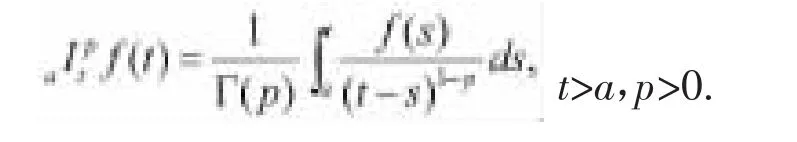
定義1.2.[2]p（p＞0）階黎曼-劉維爾導數定義為：

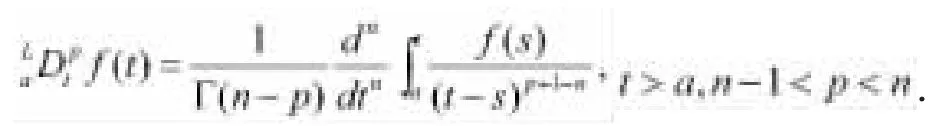
定義1.3.下限為a的p階Caputo導數定義為：

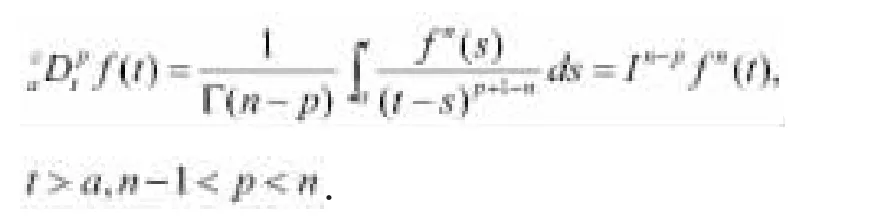
如果f是X上取值的抽象函數，則定義1.1，1.2中的積分在Bochner意義下是可以取值的。

注釋1.1.假設J?R和1≤p≤∞，對于可測函數m:J?R，定義范數

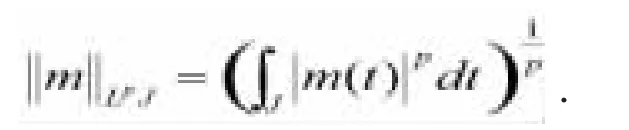
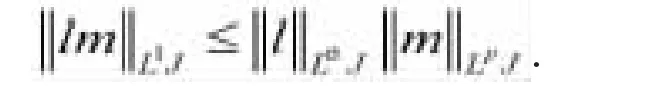
定義1.4.一個算子稱為是扇形的，假如存在常數，且M＜0，使得A的預解存在于扇形的外部，滿足

注釋1.2.研究α（0＜α＜1）階Caputo導數發展方程的柯西問題，形式如下：

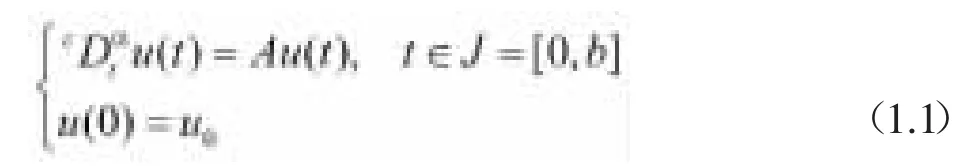
注釋1.3.[14]假如是模型（1.1）的一個解算子，則

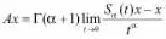
現在我們討論模型（1）適度解的定義。

根據定義1.1和1.2，在方程（1.2）積分存在的條件下，變換非局部柯西問題（1）為如下等效的積分方程

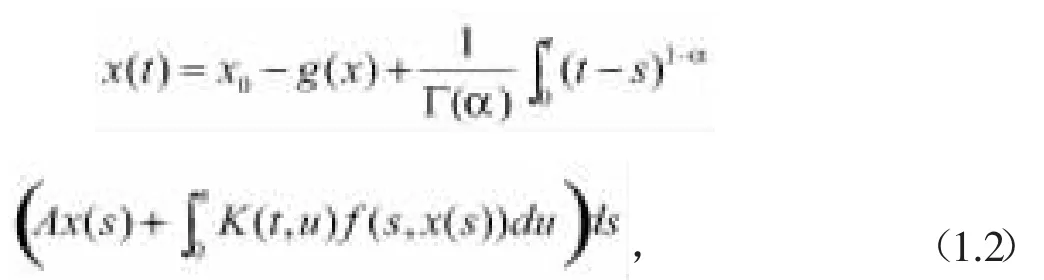
引理1.2.假設方程（1.2）成立，且A是一個扇形算子，則有

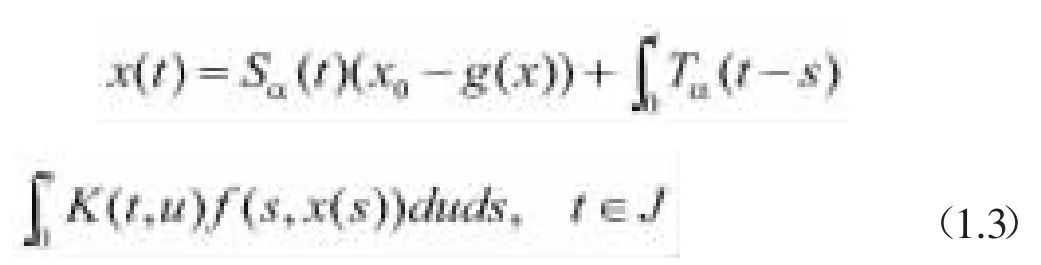
滿足

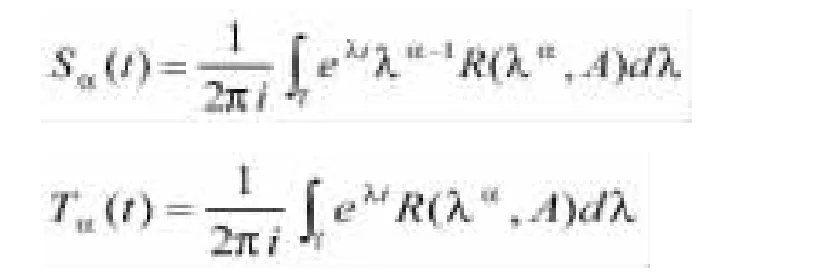
引理1.4.[1]如果以及，則對于任意的t>0，有

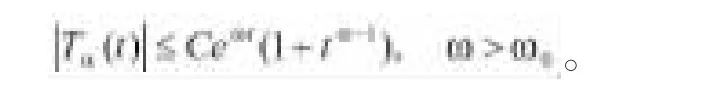
引理1.6.（Krasnoselskii不動點定理）設E是一個Banach空間，令B是E的一個有界閉凸子集。設F1與F2是B到E的壓縮，使得對于每一個x，y∈B，有F1x+ F2y∈B，如果F1是壓縮的，F2是完全連續的，則方程F1x+F2y＝x在B上有一個解。

定義1.6.函數x:J→X稱為是方程（1）的適度解，假設x滿足如下方程

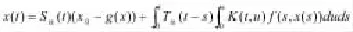
其中

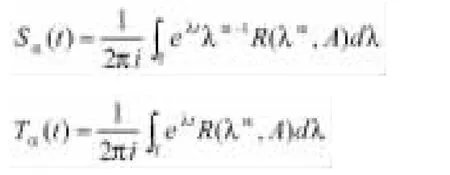
注釋1.5.假設在方程（1）中產生一個C0-半群，則得到

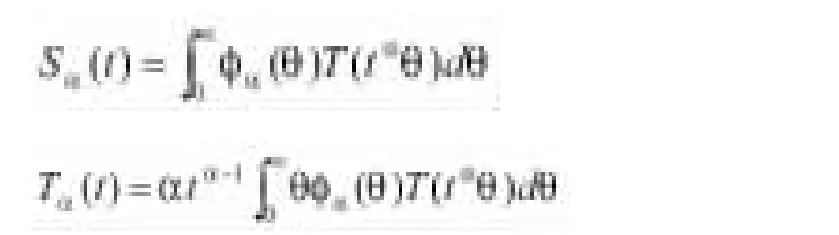
定義1.7.方程（1）稱為是在J上可控的，假如對于每一個，存在一個控制函數，使得方程（1）的一個適度解x滿足x（b）=x1.

本節給出如下的假設：

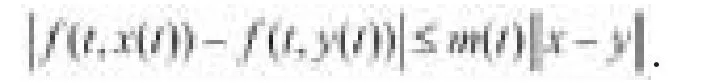
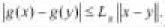
顯然，若果(H2)成立，那么下面的假設成立：

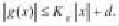
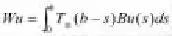
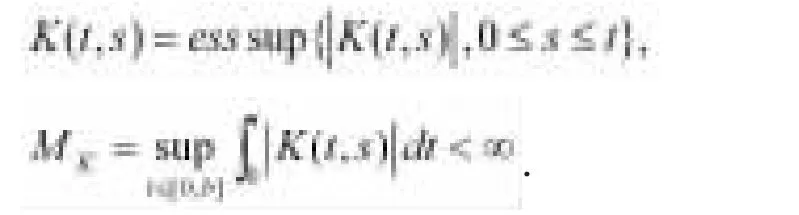
(H6)映射t→Kt從J到是連續的，此處

2　可解性與可控性結果

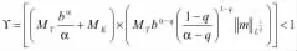
滿足的條件下，方程（1）在J上有一個適度解。

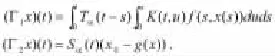
為了使如下過程更清楚，分幾步證明。

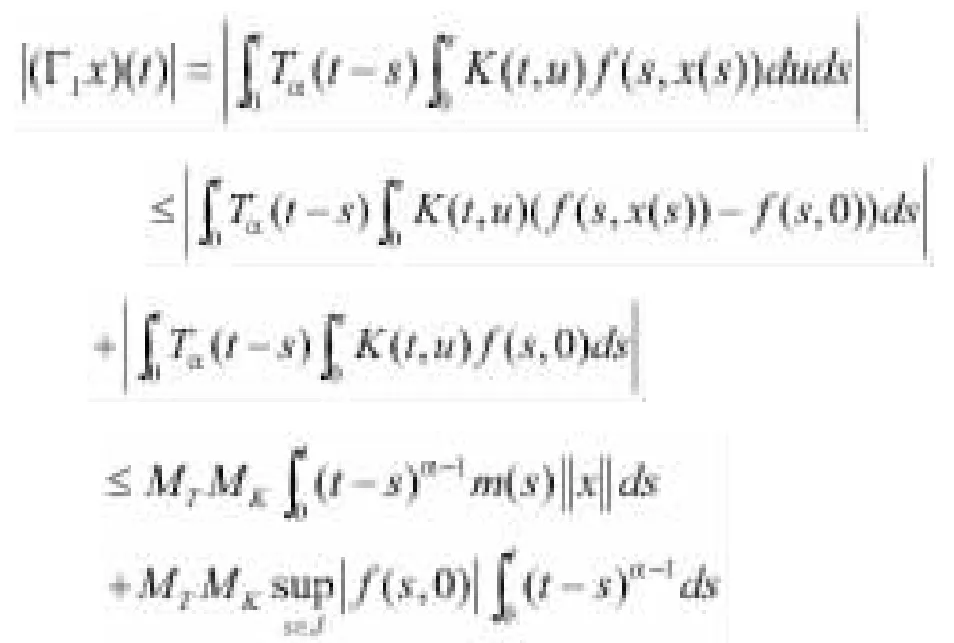
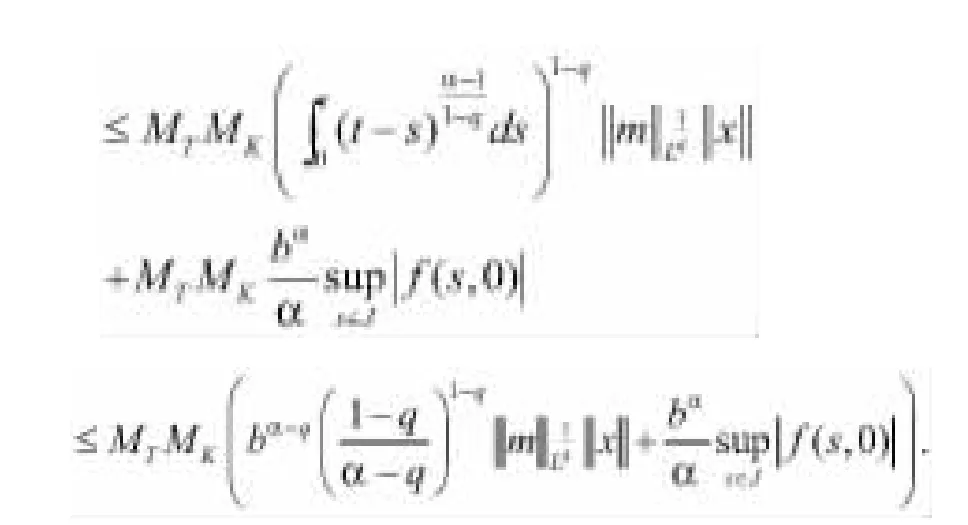
由壓縮γ＜1得到k0＞0,使得對于，有

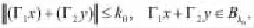
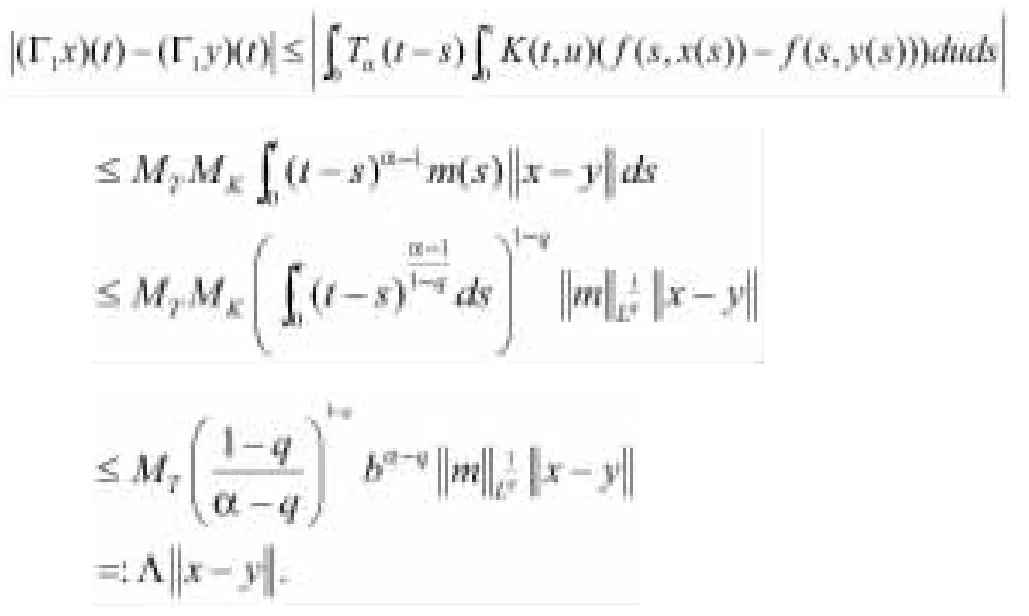
由壓縮γ＜1,獲得Λ＜1,這暗示Γ是一個壓縮映射。

步驟三.Γ2是一個完全連續的算子,也分幾步證明

首先,證明Γ2在上是連續的。對于,設.由（H’2），當n→∞,得到g（xn）→g（x）進一步得到

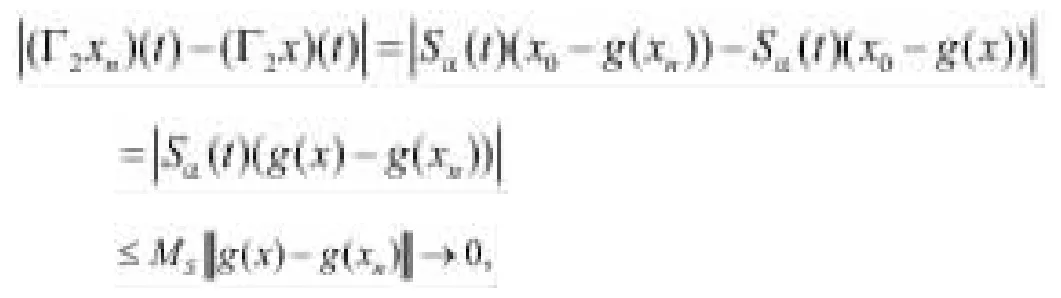
這暗示Γ2是連續的。

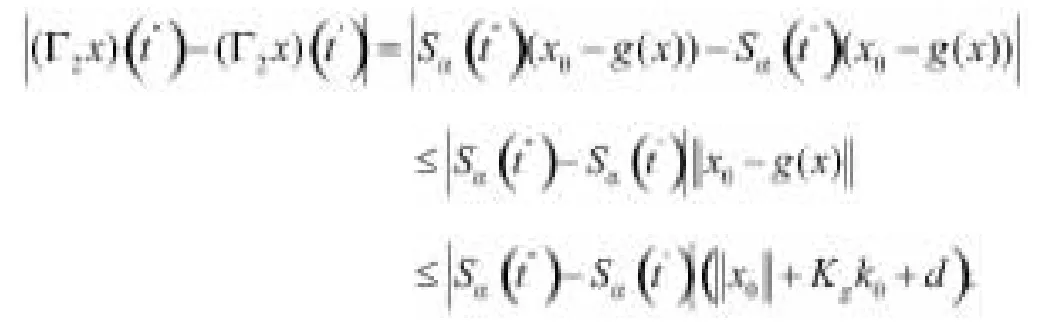
定理2.2如果(H1-H2),(H4-H6)是滿足的，則在和

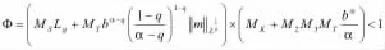
滿足的條件下，方程（2）在J上是可控的。

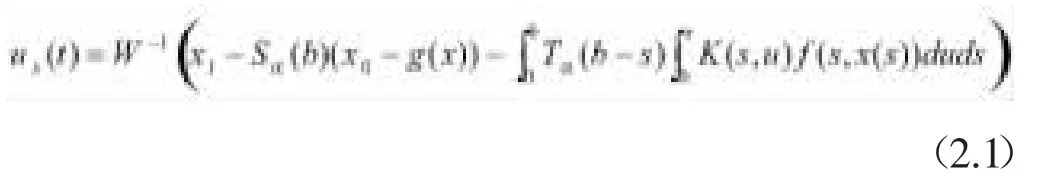
可以得到控制函數ux（t）．通過

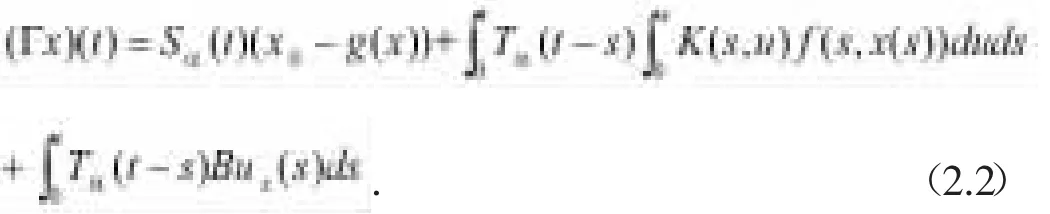
證明使用控制函數ux（t），算子Γ在C（J，X）上有一個不動點x，這個不動點是方程（2）的一個適度解。顯然，這意味著ux在有限時滯b上控制著從x0到x1的適度解x，這暗示了方程（2）在J上是可控的。

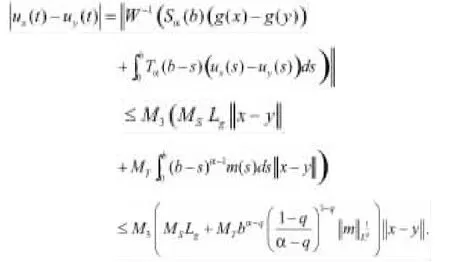
由方程（1.4），得到

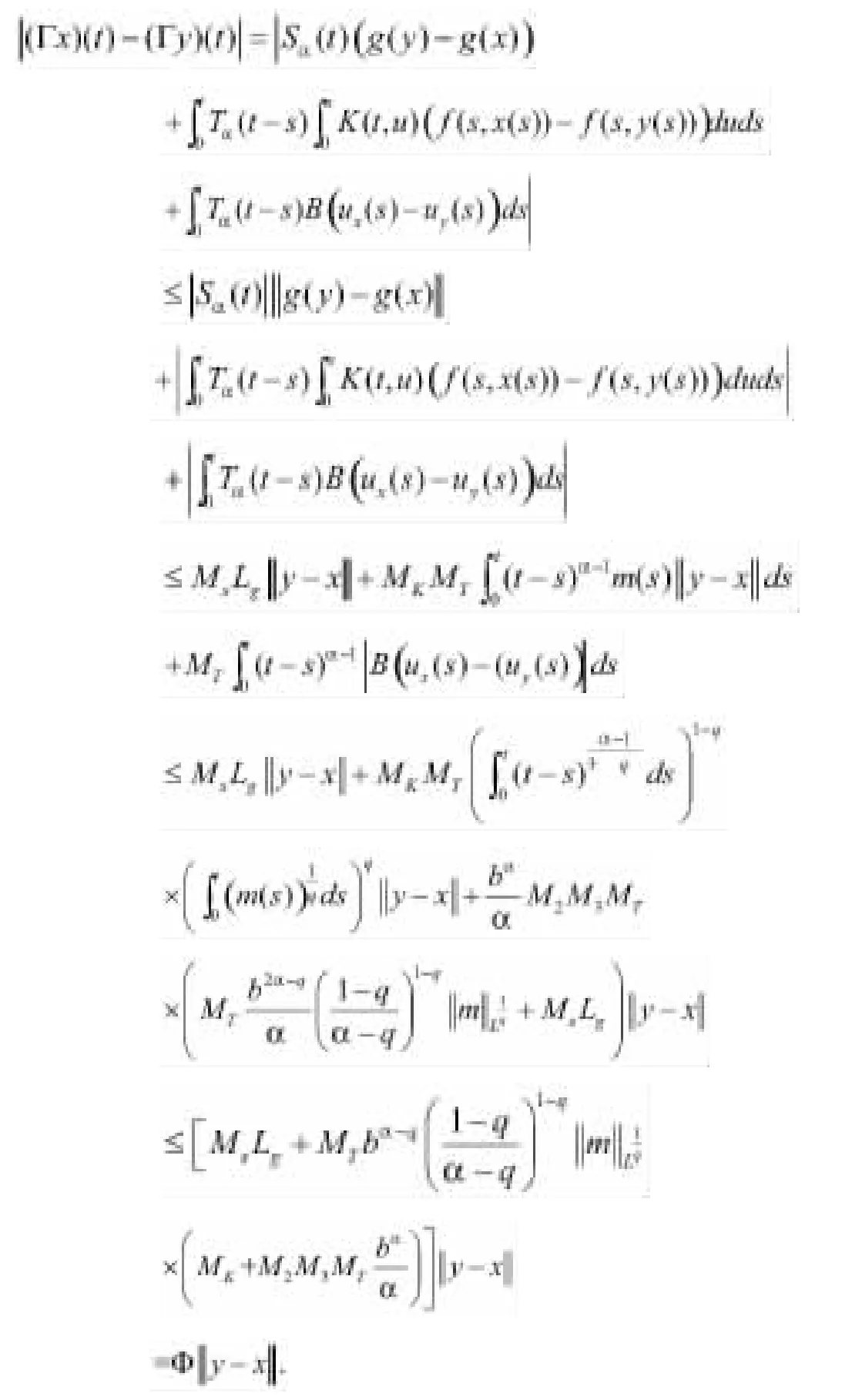
因此，Γ是一個壓縮映射，并且有一個不動點x*∈C（J，X），所以此x*是方程（2）的一個適度解，因此方程（2）在J上是可控的．證明完畢。

3　應用舉例

此處舉例討論了定理2.1的一個簡單應用，研究了形式為

的分數階偏積分微分方程，滿足?αt是階Caputo分數階偏導數，f是已知函數，

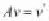
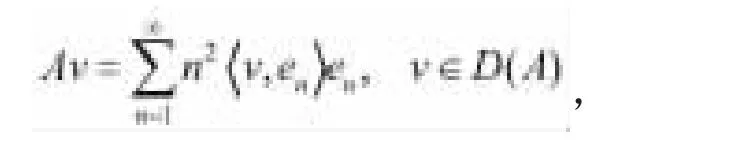
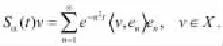
所得到的，所以（H4）是滿足的。

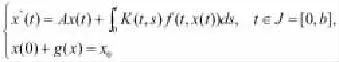
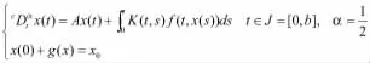
因此由定理2.1，如果（H1-H6）是滿足的，則方程（1）在[0，b]上是可解的．證明完畢。

參考文獻：

［1］K.S.Miller and B.Ross.An introduction to the fractional calculus and differential equations［M］.John Wiley and Sons, New York,NY,USA，（1993）.

［2］I.Podlubny.Fractional differential equations［J］.Academic Press,San Diego,Calif,USA,198（1999）：1-13.

［3］H.J.Lee,J.Park and J.Y.Park.Existence results for secondorder neutral functional differential and integrodifferential inclusions in Banach spaces［J］.Math.Phys.2000（2002）：1-13.

［4］K.Karthikeyan.Existence results for impulsive differential and integrodifferential equations and inclusions［M］.Bharathiar University,India，（2010）：58-70.

［5］X.B.Shu,Y.Lai and Y.Chen.The existence of mild solutions for impulsive fractional partial differential eqtations［J］. Nonlinear.Anal.74（2011）：2003-2011.

［6］E.Hernándea,D.O'Regan and K.Balachandran.On recent developments in the theory of abstract differential equations with fractional derivatives［J］.Nonlinear.Anal.73（2010）：3462-3471.

［7］Y.Zhou and F.Jiao.Existence of mild solutions for fractional neutral evolution equations［J］.Compute.Math.Appl.59 （2010）：1063-1077.

［8］G.M.Mophou.Existence and uniqueness of mild solutions to impulsive fractional differential equations［J］.Nonlinear.Anal. 72（2010）：1604-1615.

［9］X.B.Shu and Q.Wang.The existence and uniqueness of mild solutions for fractional differential equationswith nonlocal conditions of order［J］.Compute.Math.App.64（2012）：2100-2110.

［10］Y.K.Chang,J.J.Nieto and W.S.Li.Controllability of semilinear differential systems with nonlocal initial conditions in Banach spaces［J］.Optim.Theory.Appl.142（2009）：267-273.

［11］K.Balachandran and J.P.Dauer.Controllability of nonlinear system in Banach spaces:A survey［J］.Optim.Theory.Appl.115（2002）：7-28.

［12］X.Yang and H.B.Gu.Complete controllability for fractional

evolution equations［J］.Abstract and Applied Analysis. （2014）：Article ID 730695,8 pages.

［13］K.Yosida.Functional Analysis［M］.sixth ed.Springer, Berlin,1980.

［14］N.I.Mahmudov and S.Zorlu.On the approximate controllability of fractional evolution equations with compact analytic semigroup［J］.Compute.Appl.Math.259（2014）：194-204.

作者簡介：高媛（1988-），女,漢族，甘肅張掖人，在讀研究生，主要研究方向：分數階積分微分方程的可解性。

收稿日期：2015-12-25

中圖分類號：O175

文獻標識碼：A