城市工況下最小安全車距控制模型和避撞算法*

劉貴如,周鳴爭，王陸林 ,王 海

(1．安徽工程大學計算機與信息學院，蕪湖 241000； 2.奇瑞汽車股份有限公司前瞻技術(shù)研究院，蕪湖 241006)

2016188

城市工況下最小安全車距控制模型和避撞算法*

劉貴如1,周鳴爭1，王陸林2,王 海2

(1．安徽工程大學計算機與信息學院，蕪湖 241000； 2.奇瑞汽車股份有限公司前瞻技術(shù)研究院，蕪湖 241006)

鑒于傳統(tǒng)安全距離模型適應(yīng)性差、模型參數(shù)須預(yù)先確定和車距控制偏差大的缺陷，提出一種最小安全車距控制模型和避撞算法。通過視覺和雷達傳感器實時監(jiān)測前方車輛，針對前方車輛行駛狀態(tài)和不同類型車輛制動性能差異，給出相應(yīng)的安全距離估算模型、最小安全車距控制模型與算法；為了保證車距控制精度，采用周期閉環(huán)控制方法。該算法應(yīng)用于奇瑞智能自主跟車系統(tǒng)，經(jīng)過2種工況、5種初始車速和2 000次的城市道路試驗。結(jié)果表明：最小安全車距均保持在1～2m內(nèi)，控制偏差精度在±0.5m內(nèi)。該算法在各種城市工況下均具有很較高的車距控制精度，能有效提高車輛的主動安全性、駕乘舒適性和道路行車利用效率。

汽車工程；安全距離模型；最小安全車距控制模型；避撞算法

前言

隨著汽車主動安全技術(shù)的快速發(fā)展和用戶對車輛安全需求的不斷提高，針對車輛防撞[1]及其關(guān)鍵算法[2]的研究受到廣泛關(guān)注。國內(nèi)外專家學者對此提出了一些安全距離模型，主要有固定車距法、車頭時距法、駕駛員估計模型法[3]等。但是各模型也存在一些共性問題，模型參數(shù)需要事先確定，同時沒有綜合考慮駕駛員、行駛路面以及整車制動性能等方面的差異性，適應(yīng)性差，估算報警距離和制動距離過大或者過小，無法同時兼顧車輛安全性和道路行車效率[4]。

為了解決以上安全距離模型存在的不足，針對車輛縱向行駛場景，本文中提出了一種改進的自適應(yīng)安全距離模型、最小安全車距控制模型及其控制算法，充分考慮了不同車輛制動性能和駕駛員之間的個性差異、行駛路面、前車制動性能和行駛狀態(tài)等影響因素，以及通過測量值作為模型輸入的安全距離估算方法存在的滯后性和失效性，針對不同工況提出具體的估算模型，以控制車輛最小安全距離為最終目的，在避撞過程中不斷調(diào)整本車制動減速度，對安全距離進行動態(tài)閉環(huán)控制，保證本車和前車相對速度消除后，最小安全距離保持在一個恒定的范圍，避免過大或者過小，既提高了系統(tǒng)距離估算精度和防碰撞概率，同時也保證了駕乘舒適性和行車效率。

1 典型的安全距離模型

安全距離模型根據(jù)本車和前車的運行狀態(tài)和相關(guān)因素實時動態(tài)估算報警距離和實施制動干預(yù)距離，保證車輛不發(fā)生追尾碰撞[5]，距離估算的可靠性和估算精度直接影響系統(tǒng)的行車安全、駕乘舒適性以及道路行車效率，是車輛前方防撞系統(tǒng)報警提醒和實施制動的依據(jù)。而影響安全距離估算的因素包括模型本身以及相關(guān)參數(shù)兩個方面[6]。

1.1 固定安全距離模型

固定安全距離模型以預(yù)先設(shè)定的距離作為判斷依據(jù)，小于該值就報警。假設(shè)Dg表示安全距離，模型可表示為Dg=S,S根據(jù)本車車速從預(yù)先設(shè)定的安全距離列表中選取，但是該算法缺乏靈活性，沒有考慮車輛行駛環(huán)境和駕駛員特性等因素，實用性差[3]。

1.2 自由滑行時間模型

自由滑行時間模型以預(yù)先設(shè)定的自由滑行時間為依據(jù)進行安全距離計算，假設(shè)Ds表示安全距離,模型表示為

Ds=vb×ts+L

(1)

式中：vb為本車車速；ts為本車自由滑行時間；L為適當停車距離。該算法簡單，適用于勻速跟車行駛的城市交通環(huán)境，不適用于前方靜止車輛，且適應(yīng)性差。L值設(shè)置過大，則大部分場景會造成相鄰車道車輛超車、降低行車效率；L值設(shè)置過小，則容易發(fā)生追尾碰撞。另外,自由滑行時間T參數(shù)只能預(yù)先設(shè)定一個經(jīng)驗值，針對不同的駕駛員反應(yīng)時間差異，安全距離估算精度偏差較大[4]。

1.3 駕駛員預(yù)估安全距離模型

駕駛員預(yù)估安全距離模型由駕駛員估計本車與前車相對車速、相對距離以及估計時間tg內(nèi)車輛運行變化[3]對安全距離進行估計。假設(shè)Dgs表示安全距離,則模型可表示為

(2)

式中：vr為本車與前車初始相對車速；af為前車減速度；m為tg時間后本車與前車相對距離等于駕駛員的最小容忍距離。本模型重視駕駛員的主觀感受，但是m的取值需要同時兼顧前車靜止、減速和勻速行駛工況比較困難，參數(shù)tg也較難確定，安全距離模型估算的準確性難以保證。

1.4 車間距保持安全距離模型

車間距保持安全距離模型根據(jù)預(yù)先設(shè)定的自由滑行時間(即駕駛員響應(yīng)時間)、本車車速、本車與前車相對車速、本車減速度、前車減速度以及相對距離預(yù)估預(yù)警安全距離和主動制動安全距離[3-4]。假設(shè)Dw表示預(yù)警指令發(fā)出時本車與前車相對距離，Dz表示制動干預(yù)指令發(fā)出時本車與前車相對距離。當前方目標處于靜止狀態(tài)時：

(3)

(4)

式中:ab為本車制動減速度估計值；d為相對速度消除后本車和前車的最小安全距離。

當前方目標車輛處于運動狀態(tài)時：

(5)

(6)

式中vf為前車當前車速。

本模型針對前車運行和靜止兩種工況給出了對應(yīng)模型，同時考慮了駕駛員響應(yīng)時間，本車和前車制動減速度以及最小安全距離。但是沒有考慮制動系統(tǒng)協(xié)調(diào)時間，即發(fā)出制動指令到車輛開始減速的時間和開始制動到制動減速度達到最大時的制動距離，且相關(guān)參數(shù)為根據(jù)前期試驗數(shù)據(jù)、相關(guān)標準和經(jīng)驗統(tǒng)計值預(yù)先設(shè)定，不能根據(jù)車輛實際的運行環(huán)境進行修正，在個別極端環(huán)境下，可能出現(xiàn)安全距離過小發(fā)生碰撞的危險或者安全距離過大導(dǎo)致道路行車效率降低[3]。

本文中針對以上典型的安全距離模型存在的缺點，提出自適應(yīng)安全距離估計模型和最小安全車距控制模型。

2 改進的安全車距估計和控制模型

根據(jù)車輛在避撞過程中本車和前車不同的運行狀態(tài)，給出對應(yīng)的安全距離估算模型。最終的目的是，當本車和前車相對速度消除后(包括本車和前車均停止的情形)本車和前車的最小安全距離保持在一個穩(wěn)定的范圍。前車運行狀態(tài)包括靜止、運行中減速行駛(包括緊急制動停止)；本車運行狀態(tài)包括正常運行、運行中減速行駛(包括緊急制動停止)等工況，結(jié)合實際的場景給出典型工況的預(yù)警、制動干預(yù)安全距離估算模型和最小安全車距控制模型。

2.1 前車靜止工況

2.1.1 安全距離估算模型

該工況針對本車在正常運行中，突然發(fā)現(xiàn)前方停止的車輛。假設(shè)本車無法轉(zhuǎn)向避讓的情況下，只能采取縱向減速避撞。本車由初始速度開始減速停車，則該工況下預(yù)警安全距離和制動干預(yù)距離估算模型為

(7)

(8)

式中：td和j分別為駕駛員響應(yīng)時間和系數(shù)；tz和k為制動協(xié)調(diào)時間和系數(shù)；l為本車制動減速度估計值系數(shù)，通過路面識別模塊進行調(diào)整和修正，調(diào)整模型中本車和前車制動減速度ab預(yù)設(shè)值，以匹配當前行駛路面[10-11]。式(7)和式(8)適用于初始估計。當本車進入制動干預(yù)狀態(tài)后，如果本車從開始制動到停止，保持恒定的減速度，則d值可能偏大或者偏小，與理想的1～2m的安全距離偏差較大，所以還需要建立制動過程中的最小安全車距閉環(huán)控制模型，保證本車與前車相對速度消除后最小安全距離為期望的值，與理想的1～2m的安全距離偏差較小。

2.1.2 最小安全車距控制模型

假設(shè)Dh為本車制動過程中本車和前車安全距離估計值，D為雷達周期測量的本車與前車相對距離，則該工況最小安全車距控制模型為

(9)

理想情況下每個測距周期測量的相對距離D應(yīng)該和Dh接近，保持在一定的誤差范圍。如果D過大則d可能過大，可以適當減小制動減速度，避免急減速造成駕乘人員的不舒適感，同時提高道路行車效率。如果D過小則d可能過小，容易增加碰撞風險，安全優(yōu)先，可以適當加大制動減速度保證行車安全為前提。本模型通過毫米波雷達實時探測本車和前車的相對距離，通過調(diào)整系數(shù)l調(diào)整本車制動減速度對制動距離進行閉環(huán)調(diào)整，實現(xiàn)最小安全距離d值的穩(wěn)定和精確控制。

2.2 前車行駛工況

2.2.1 安全距離估算模型

該工況針對本車在正常運行中，突然發(fā)現(xiàn)前車緊急減速。假設(shè)本車無法轉(zhuǎn)向避讓的情況下，采取制動減速避撞，前車運行狀態(tài)即最終車速無法預(yù)知，故Dw和Dz的估計以前車最終停止，后車也停止為假設(shè)前提，則該工況下安全距離估算模型為

Dw=(vf-vb)×j×td+(vf-vb)×k×tz+

(10)

(11)

式中m為前車制動減速度估計值修正系數(shù)。

通過自學習模塊對本車制動性能進行評估，根據(jù)評估結(jié)果對參數(shù)l進行修正，調(diào)整模型中本車制動減速度ab預(yù)設(shè)值，以匹配本車制動性能。通過自學模塊對駕駛員響應(yīng)時間的評估結(jié)果，對參數(shù)j進行修正，調(diào)整模型中駕駛員響應(yīng)時間Td預(yù)設(shè)值。通過自學習模塊對制動系統(tǒng)協(xié)調(diào)時間的評估結(jié)果，對參數(shù)k進行修正，調(diào)整模型中駕駛員響應(yīng)時間Tz預(yù)設(shè)值。通過路面識別模塊調(diào)整l和m進行修正，調(diào)整模型中本車和前車制動減速度ab與af預(yù)設(shè)值，以匹配當前行駛路面。通過對相關(guān)參數(shù)的自適應(yīng)修正，使安全距離估算更趨合理，更符合實際應(yīng)用場景，估計更準確，保證車輛不發(fā)生碰撞的同時，保持較高的行車效率、駕乘舒適性及駕駛體驗[12]。

式(10)和式(11)只適用于估計開始預(yù)警距離和制動干預(yù)距離。如果在本車減速過程中不實時調(diào)整本車制動減速度，則本車和前車相對速度消除后最小安全距離和理想的距離可能出現(xiàn)偏差過大或者過小，無法保持較高的避撞概率和行車效率[13]。要保持本車和前車相對車速消除后最小安全距離在理想范圍。針對車輛制動干預(yù)后的運行狀態(tài)工況，提出了一種閉環(huán)逼近自適應(yīng)最小安全距離估算控制模型。在本車開始制動減速后，影響d值的因素主要是前車制動距離和本車制動距離，通過調(diào)節(jié)本車制動減速度對制動距離進行調(diào)整，保證d在一個理想的范圍內(nèi)。

2.2.2 最小安全車距控制模型

前車行駛工況下最小安全車距控制模型為

(12)

式中：t為雷達測距周期。模型中前車制動減速度參數(shù)除了根據(jù)路面識別模塊進行調(diào)整外，基本保持不變。在每個雷達的距離測量周期t內(nèi)，通過調(diào)整系數(shù)l，調(diào)整本車制動減速度，使得測量值D接近于估計值Dh，采用這種估算方法則不需要考慮前車最終的運行車速，在實際場景中實用性更強，保持d值在合理范圍內(nèi)。ab與af根據(jù)毫米波雷達實時采集的相對車速和本車實時車速進行更新，形成一個閉環(huán)預(yù)估模型，通過實時調(diào)整本車制動減速度參數(shù)系數(shù)l調(diào)整相對安全距離，使得相對車速消除后相對距離d更趨于合理。式(12)為本車實施制動后本車與前車最小安全間距控制模型，其閉環(huán)控制過程與駕駛員人為避撞的過程非常相似，可以在防止發(fā)生碰撞的前提下，保持足夠小的安全間距，保證駕乘舒適性和道路行車效率[14]。

式(7)～式(12)中相關(guān)參數(shù)預(yù)值的確定:td一般取值范圍為0.4～1.5s，典型值為1s;tz一般取值為200～400ms,典型值為300ms；ab一般取值范圍為3.0～9.8m/s2,轎車制動減速度典型值為5.5m/s2，貨車制動減速度典型值為3.6m/s2。系數(shù)j,k,l,m預(yù)設(shè)置均為1，變化范圍為0.5～1.5；d取值范圍為1～2m。

2.3 算法運行流程

兩種工況下算法運行流程圖見圖1，其不同之處除了模型不同外，制動干預(yù)判斷的條件不同。當滿足vf=0和vb>0時，為前車靜止，本車運行工況，流程圖中預(yù)警距離和制動干預(yù)距離采用該工況下的估計模型。當滿足vf≠0和vf≤vb時，為前車減速行駛，本車運行工況，流程圖中預(yù)警距離和制動干預(yù)距離采用該工況下的估計模型。在避撞過程中先預(yù)警，后干預(yù)，當進行制動干預(yù)后，通過適時調(diào)整本車制動減速度實現(xiàn)本車與前車最小安全距離的閉環(huán)精確控制，在控制過程中，實時判斷兩種工況的條件，如不滿足任一一個條件，則退出預(yù)警和制動干預(yù)模式。

圖1 算法運行流程圖

3 實車驗證與結(jié)果分析

3.1 安全距離估算算法的比較分析

模型中相關(guān)參數(shù)在參考相關(guān)標準以及經(jīng)驗值的基礎(chǔ)上賦以典型預(yù)設(shè)值，但是參數(shù)還需要在后期試驗過程中進行標定，使參數(shù)的設(shè)置和系統(tǒng)更好地匹配，系統(tǒng)在兩種工況下進行試驗。

本文中對常用的幾種安全距離模型與本模型進行了對比分析。假設(shè)FSDM表示固定安全距離模型，RSTM表示自由滑行時間模型，DFDM表示駕駛員預(yù)估安全距離模型，DKSDM表示車間距保持安全距離模型，MSVDCM為本文中提出的最小安全車距控制模型。在兩種工況下對各算法模型分別進行對比測試試驗及比較分析。鑒于實際測試環(huán)境和條件，提高測試的安全性，測試結(jié)果通過相對距離進行驗證，將d取值設(shè)定為11～12m的范圍。測試結(jié)果減去10m作為最終的最小安全車距。在前車停止工況下進行測試，各模型算法估計的預(yù)警距離和制動干預(yù)距離結(jié)果對比見圖2。

由圖2可見：FSDM模型估算的預(yù)警距離是不同速度區(qū)間的先驗值,相對比較固定，可以作為判斷其它算法結(jié)果是否準確的參考；其余3種安全距離模型在低速時估算的預(yù)警距離普遍偏大，容易發(fā)生過多預(yù)警而引起駕駛員的反感，而高速時估算的預(yù)警距離則普遍偏小，增大了追尾事故的風險，在實際應(yīng)用中都存在缺陷[15]。各算法模型估計的預(yù)警距離結(jié)果對比見圖2(a)。如果預(yù)警0.5～0.6s后駕駛員仍不采取制動減速措施，則制動系統(tǒng)自動干預(yù)，各算法模型估計的制動干預(yù)距離結(jié)果對比見圖2(b)。

圖2 前車靜止工況下各算法預(yù)警和制動干預(yù)距離

而本文中提出的MSVDCM最小安全車距控制模型則在確保安全的情況下，預(yù)警距離相對偏小。在實際工況中，當本車車速較大時，駕駛員一般采取轉(zhuǎn)向避撞的方式更為有效，并不需要過早報警。在后期制動干預(yù)后可以不斷調(diào)節(jié)制動減速度控制安全距離(即實現(xiàn)最小安全車距的閉環(huán)控制)，更符合駕駛員避撞特性。各模型對應(yīng)的制動干預(yù)距離相對報警距離主要體現(xiàn)在各模型中駕駛員響應(yīng)時間、制動系統(tǒng)響應(yīng)時間以及當前行駛路面等參數(shù)的差別。

3.2 最小安全距離控制算法的比較分析

3.2.1 前車靜止時算法的比較分析

不同駕駛員和制動系統(tǒng)響應(yīng)時間差異很大，導(dǎo)致制動干預(yù)過早或者過晚介入，增加了車輛追尾風險，同時也不利于有效提高道路通行效率[16]。制動干預(yù)后，車輛開始減速直到停止或者與前車相對速度為0，本車和前車的最小安全距離才是衡量各個估算模型的關(guān)鍵，也是最直接的指標，直接影響追尾碰撞風險和道路行車效率[17]。各模型參考的影響因素不同，最終的最小安全距離差異較大。在前車靜止工況下，各算法最小安全距離測試結(jié)果見表1。

表1 前車靜止工況下最小安全車距測試結(jié)果

表1中最小安全距離為實際測量得到。兼顧安全和行車效率，這個距離一般保持在1～2m內(nèi)。首先，隨著兩車的距離越來越近，相對速度也越來越小，最小安全距離保持在1～2m內(nèi)是沒有風險的。其次，一般雷達的探測更新周期為50ms，加上控制策略運行時間為50ms，共計100ms。假如車速為10km/h近距離接近，該時間段內(nèi)滑行距離估計為0.3m，加上雷達近距離探測誤差為0.5m，所以距離保持在1～2m是安全的。如果距離過小，尤其是小于1m的情況下，發(fā)生碰撞的風險較大。而大于2.5m，則距離過大，一方面不利于提高道路行車效率，另一方面距離過大，在國內(nèi)的交通狀況下，容易導(dǎo)致后方或者左側(cè)車道車輛插隊，引起交通秩序混亂[18]。

從表1數(shù)據(jù)可以看出，F(xiàn)SDM模型根據(jù)預(yù)先估計的距離實施制動，最終的最小安全距離接近4m，距離過大，行車效率偏低，但是無安全隱患。而RSTM模型和DFDM模型則由于不同的駕駛員反應(yīng)時間差異以及對前方目標感知的差異，數(shù)據(jù)可能偏大或者偏小，尤其是本車車速較高的情況下，安全距離估算誤差相對增大，增加了追尾碰撞風險[19]。DFDM模型在車速較高的情況下，憑人的主觀預(yù)測安全距離偏差大，極易造成車輛追尾事故，也缺乏靈活性。同時須要通過先驗數(shù)據(jù)，得到滑行時間參數(shù)值，測試結(jié)果最小安全距離偏小，小于1m，存在安全隱患，效果較差。DKSDM模型同時考慮了駕駛員響應(yīng)時間，本車和前車制動減速度以及先驗數(shù)據(jù)，最小安全距離相對前3種模型，距離更趨于合理，但是針對變換的行車環(huán)境，也可能會出現(xiàn)過大或者過小的情況。各模型均沒有考慮實際行駛工況，在附著系數(shù)較小的冰雪路面，發(fā)生追尾的概率很高[21]。

而本文中提出的MSVDCM控制模型既考慮了駕駛員響應(yīng)時間，也考慮了制動系統(tǒng)的協(xié)調(diào)時間和路面狀況，相關(guān)參數(shù)在前期數(shù)據(jù)標定的基礎(chǔ)上通過自適應(yīng)模塊進行實時修正，以適應(yīng)當前駕駛員和行駛工況。同時在此基礎(chǔ)上引入了安全距離閉環(huán)控制方法，實時調(diào)節(jié)制動減速度，對安全距離進行閉環(huán)控制，根據(jù)實際探測相對距離和安全距離估算值進行對比，根據(jù)對比結(jié)果不斷調(diào)整本車制動減速度，同時參考路面識別模塊輸出的路面附著系數(shù)參數(shù)對制動減速度進行修正。確保本車車速為0時，本車和前方車輛或者目標的最小安全距離保持在1～2m范圍內(nèi)。克服了各算法在對應(yīng)的初始車速下最終的最小安全距離偏大或者偏小的問題，既避免了車輛追尾事故，同時提高了道路行車效率，在車輛停止前的低速階段安全距離的控制逼近于最小安全距離，使最小安全距離控制更精確，更穩(wěn)定，具有很好的魯棒性。

3.2.2 前車運行時算法的比較分析

與前車靜止工況相比，前車減速行駛工況不僅要考慮本車的運行狀態(tài)而且還要考慮前車的運行狀態(tài)，報警距離不僅與相對速度有關(guān)，而且與本車車速有關(guān)，預(yù)警距離和制動干預(yù)距離需要實時計算。但是最小安全距離始終保持在1～2m范圍內(nèi)。測試結(jié)果見表2。

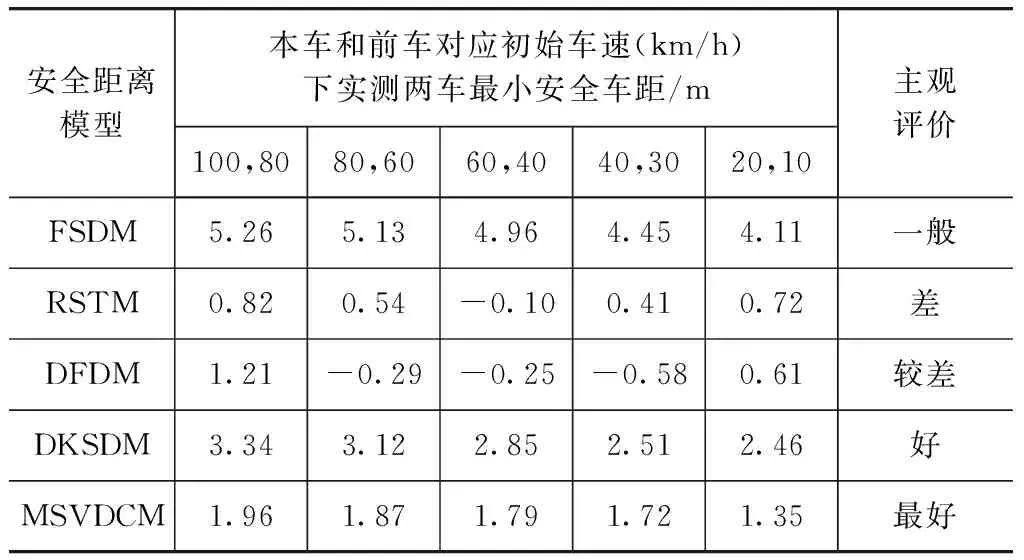
表2 前車運行工況下最小安全車距測試結(jié)果

從表2測試結(jié)果看，各安全距離模型在前車運行工況下最小安全距離估計性能和表1基本一致。只是各算法在兩種工況下最小安全距離略有差異，與各算法先驗標定參數(shù)以及模型不能很好地適應(yīng)實際運行工況有關(guān)，靈活性較差。當本車和前車在不同車速下，由于駕駛員的主觀估計存在差異[22]，故各車速下的最小安全距離存在差異，本車車速和相對車速越低，最小安全距離估計偏差越小，符合駕駛員實際的安全距離估計特性[23]。但是由于各算法自身的缺陷，導(dǎo)致最小安全距離估計偏大或偏小，既不利于行車安全，也不利于道路行車效率。

而本文中提出的MSVDCM最小安全車距控制算法引入了距離周期閉環(huán)控制，克服了各模型憑借先驗參數(shù)估算安全距離偏差較大的缺陷，在本車和前車任意車速，以及不同駕駛員在各種路況下均能將最小安全距離控制在1～2m范圍內(nèi)，具有很好的適應(yīng)性和穩(wěn)定性。

4 結(jié)論

本文中分析了影響安全預(yù)警距離和制動干預(yù)距離估算的各個因素，在分析現(xiàn)有模型和安全預(yù)警算法的基礎(chǔ)上，從駕駛員開車體驗出發(fā)，結(jié)合制動過程運動學分析，提出一種最小安全車距控制模型及避撞算法。通過理論分析、仿真以及實際場景測試，本文中提出的預(yù)警和制動干預(yù)距離估算模型結(jié)合最小安全車距控制模型及算法，能夠保證在前車靜止或者運行工況下，本車和前車的最小安全距離保持在1～2m范圍內(nèi)，既保證了行車安全，同時也提高了道路行車效率，符合駕駛員主觀感受，接近于駕駛員實際制動干預(yù)過程，易于工程化。通過實車試驗，驗證了該算法的有效性。

[1] 王暢,徐遠新,付銳,等.應(yīng)用于換道預(yù)警系統(tǒng)的潛在危險目標辨識算法[J].長安大學學報(自然科學版),2015(1):98-105.

[2] 牛潤新,夏靜霆,汪小華,等.智能車輛路徑巡航和自主避障的觸須算法[J].交通運輸工程學報,2010(12):53-58.

[3] 劉剛,侯德藻,李克強,等.汽車主動避撞系統(tǒng)安全報警算法[J].清華大學學報(自然科學版),2004,44(5):697-700.

[4] 許倫輝,羅強,吳建偉,等.基于最小安全距離的車輛跟馳模型研究[J].公路交通科技,2010(10):95-106.

[5] 游峰,張榮輝,王海瑋,等.基于縱向安全距離的超車安全預(yù)警模型[J].華南理工大學學報(自然科學版),2013,8(41):87-92.

[6] 邱小平,于丹,孫若曉,等.基于安全距離的元胞自動機交通流模型研究[J].交通運輸系統(tǒng)工程與信息,2015(4):54-60.

[7] 黨宏社,韓崇昭,段戰(zhàn)勝.汽車防碰撞報警與制動距離的確定[J].長安大學學報(自然科學版),2002(11):89-91.

[8] 裴曉飛,劉昭度,馬國成,等.汽車主動避撞系統(tǒng)的安全距離模型和目標檢測算法[J].汽車安全與節(jié)能學報，2012,3(1):26-33.

[9] 劉雨童,張駿,史忠科.汽車啟動時安全距離模型的改進及其驗證[J].西北工業(yè)大學學報,2014(10):725-729.

[10] 張彪,張俊智,劉昭度.基于車身減速度估計的ABS路面識別方法[J].中國公路學報,2011(3):109-113.

[11] 裴曉飛,劉昭度,齊志權(quán).汽車縱向集成控制系統(tǒng)的路面識別方法[J].中國公路學報,2014(5):177-182.

[12] 裴曉飛,齊志權(quán),王保鋒,等.汽車前向主動報警/避撞策略[J].吉林大學學報(工學版),2014(5):599-604.

[13] 李霖,朱西產(chǎn),董小飛,等.自主緊急制動系統(tǒng)避撞策略的研究[J].汽車工程,2015,37(2):168-174.

[14] 李霖,賀錦鵬,劉衛(wèi)國,等.基于駕駛員緊急制動行為特征的危險估計算法[J].同濟大學學報(自然科學版),2014(1):109-114.

[15] 郭應(yīng)時,王暢,付銳,等.城市道路環(huán)境中駕駛?cè)藨?yīng)激響應(yīng)時間特性[J].中國公路學報,2013(11):135-142.

[16] 呂集爾,朱留華,鄭容森，等.駕駛員反應(yīng)時間對行車安全的影響[J].交通運輸系統(tǒng)工程與信息,2014(4):80-86.

[17] 王龐偉,余貴珍,王云鵬,等.基于滑模控制的車車協(xié)同主動避撞算法[J].北京航空航天大學學報,2014(2):268-273.

[18] 侯德藻,劉剛,高鋒，等.新型汽車主動避撞安全距離模型[J].汽車工程,2005,27(2):186-199.

[19] 唐陽山,江振偉,白艷，等.汽車防碰撞安全距離模型及仿真研究[J].遼寧工業(yè)大學學報(自然科學版),2008(10):324-326.

[20] 高振海,吳濤,趙會.車輛虛擬跟隨避撞中駕駛?cè)酥苿訒r刻模型[J].吉林大學學報(工學版),2014(9):1233-1239.

[21] James R Ward, Gabriel Agamennoni, Stewart Worrall, et al.Extending time to collision for probabilistic reasoning in general traffic scenarios[J].Transportation Research Part C,2015, 51:66-82.

[22] Vicente Milanes, Joshue Perez, Jorge Godoy, et al.A fuzzy aid rear-end collision warning/avoidance system[J].Expert System with Applications,2012,39:9097-9107.

[23] Emeli Adell, Andras Varhelyi, Mario Dalla Fontana.The effects of a driver assistance system for safe speed and safe distance-A real-life field study[J].Transportation Research Part C,2011,19:145-155.

Control Model for Minimum Safe Inter-vehicle Distance and Collision Avoidance Algorithm in Urban Traffic Condition

Liu Guiru1, Zhou Mingzheng1, Wang Lulin2& Wang Hai2

1.CollegeofComputerandInformationScience,AnhuiPolytechnicUniversity,Wuhu241000；2.ProspectiveTechnologyResearchInstitute,CheryAutomobileCo.,Ltd.,Wuhu241006

In view of the defects of traditional safe distance models (poor adaptability, the necessity of presetting model parameters and large control deviation of inter-vehicle distance), a control model for minimum safe inter-vehicle distance and a collision avoidance algorithm are proposed. Visual and radar sensors are used to monitor front vehicle. According to different driving states of front vehicle and the different brake performance of different types of vehicles, the corresponding safe distance estimation model and the control model and algorithm for minimum safe inter-vehicle distance are used, and for ensuring the control accuracy of inter-vehicle distance, a periodic closed-loop control method is adopted. The algorithms are applied to Chery intelligent autonomous following car system to conduct 2,000 tests on urban road with two conditions and five initial speeds. The results show that the minimum safe inter-vehicle distance is kept within the range of 1-2 meters with a control deviation less than ± 0.5 meters, indicating that the algorithms proposed can achieve high control accuracy in various urban conditions and effectively enhance the active safety performance and ride comfort of vehicle and road utilization efficiency.

automotive engineering; safe distance model; minimum safe inter-vehicle distance control model; collision avoidance algorithm

*國家自然科學基金(91120307)、安徽省自然科學基金(TSKJ2015B12)、安徽工程大學計算機應(yīng)用技術(shù)重點實驗室開放基金(JSJKF201514)和江蘇省六大人才高峰項目(2014-DZXX-040) 資助。

原稿收到日期為2016年3月8日，修改稿收到日期為2016年5月26日。